8.2.2 消元---解二元一次方程组课件
文档属性
| 名称 | 8.2.2 消元---解二元一次方程组课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-14 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
人教版 七年级数学下
8.2加减消元法
---解二元一次方程组
学习目标
1.掌握加减消元法的意义;
2.会用加减法解二元一次方程组.(重点)
回顾旧知
10-x
2x+(10-x)=16
同学们观察,这两个方程中y的系数有什么关系?利用这种关系你能发现新的消元法吗?
x+y=10 ①
2x+y=16 ②
1.用代入法解二元一次方程组
解:由①得:y= ③
把③代入②得:
解得:x=6
将x=6代入③得:y=4
所以这个方程组的解是:
x=6
y=4
我们发现两个方程中y的系数相等,进而想到利用等式的性质将两个方程相减就可以消去y, ①- ②或②- ①都行,具体分析如下。
合作探究---加减消元法
1.用解二元一次方程组
①
②
分析: ②- ①
② 左边 - ①左边 = ②右边 - ① 右边
2x+y -x-y=6
x=6
(2x+y)
- (x+y)
= 16
-10
x+y=10 ①
2x+y=16 ②
1.解二元一次方程组:
合作探究---加减消元法
所以这个方程组的解是:
解:由②-①得: x=6
把x=6代入①得: 6+y=10
解得: y=4
方法总结:
同一未知数的系数
时,
把两个方程的两边分别 !
相等
相减
合作探究---加减消元法
3x +10 y=2.8 ①
15x -10 y=8 ②
解:把 ①+②得: 18x=10.8
x=0.6
把x=0.6代入①,得:
3×0.6+10y=2.8
解得:y=0.1
2、解方程组:
所以这个方程组的解是
x=0.6
y=0.1
同学们观察,这两个方程中y的系数有什么关系?
方程①、②中未知数y的系数互为相反数,可以利用两个方程相加消去未知数y.
方法总结:
同一未知数的系数
时,
把两个方程的两边分别 !
互为相反数
相加
将x=0.6代入②可以吗?
合作探究---加减消元法
归纳总结:
像上面这种解二元一次方程组的方法,叫做加减消元法,
简称加减法.
当方程组中两个方程的同一未知数的系数互为相反数或相等时,把这两个方程的两边分别相加(系数互为相反数)或相减(系数相等)来消去这个未知数,得到一个一元一次方程,进而求得二元一次方程组的解.
合作探究---加减消元法
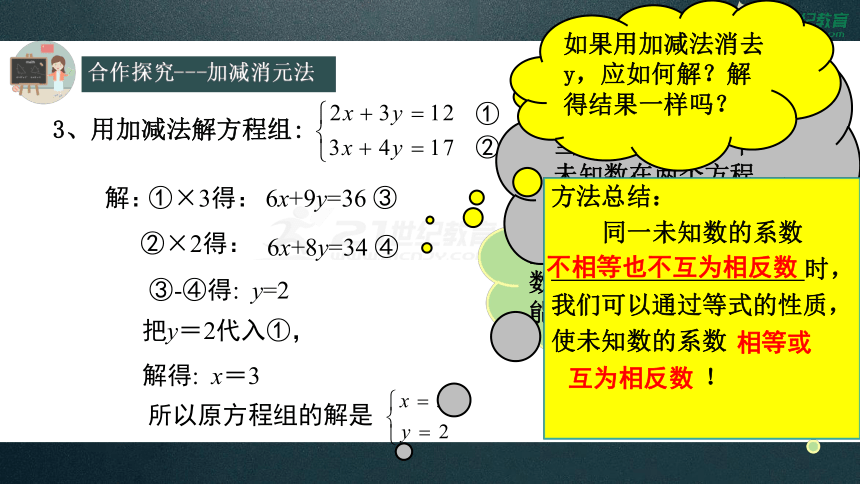
3、用加减法解方程组:
①
②
①×3得:
所以原方程组的解是
解:
③-④得: y=2
把y=2代入①,
解得: x=3
②×2得:
6x+9y=36 ③
6x+8y=34 ④
同学们再观察,这两个方程中x、y的系数有什么关系?
方程①、②中未知数x、y的系数既不互为相反数,也不相等,所以不能直接通过加减来消元.
为了消元,我们可以在方程两边乘适当的数,使同一个未知数在两个方程中的系数相等或相反,比如我们对x的系数进行改造。
如果用加减法消去y,应如何解?解得结果一样吗?
方法总结:
同一未知数的系数
时,
我们可以通过等式的性质,
使未知数的系数
!
不相等也不互为相反数
相等或
互为相反数
小试牛刀
1、用加减法解下列方程组:
小试牛刀
2、已知 , 则a+b等于_____.
3
①
②
知识点拨:方法一:直接解方程组,求出a与b的值,然后就可以求出a+b.
方法二:?+?得 :4a+4b=12, a+b=3.
变式训练:已知x、y满足方程组 求代数式x-y的值.
解: ②-①得:2x-2y=-1-5,
得:x-y=-3.
总结归纳
变形后加减消元法解方程组的主要步骤有哪些?
变形
变同一个未知数的系数相同或互为相反数
加减
求解
写解
写出方程组的解
消去一个未知数化为一元一次方程
求出一个未知数的值
回代
代入原方程求出另一个未知数的解
消元先看相同未知数系数的最小公倍数
用加减法解决实际问题
分析:题目中存在的两个等量关系:
2×(2台大收割量+5台小收割量)=______
5×(3台大收割量+2台小收割量)=______
例4 2台大收割机和5台小收割机均工作2h共收割小麦3.6 hm2,3台大收割机和2台小收割机同时工作5h共收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
3.6hm2
8hm2
用加减法解决实际问题
解:设一台大收割机和一台小收割机每小时各收割小麦x hm2和y hm2.根据题意,得
②-①,得 ______
解得 x=_______
把x=_____ 代入①,得y=______
所以方程组的解为:
答:一台大收割机和一台小收割
机每小时分别收割小麦0.4hm2
和0.2hm2
11x=4.4
0.4
0.4
0.2
①
②
小试牛刀
1、某停车场的收费标准如下:中型汽车的停车费为12元/辆,小型汽车的停车费为8元/辆,现在停车场共有50辆中、小型汽车,这些车共缴纳停车费480元,中、小型汽车各有多少辆?
归纳总结
思考:我们现在已经学习了两种解二元一次方程组的方法,那么如何合理的选择消元法来解二元一次方程组?
(1)代入消元法:当存在未知数的系数的绝对值是1 的时候我们优先
选择代入法;
(2)加减消元法:当未知数的系数相等或者互为相反数又或者存在整
倍数关系时我们优先选择加减法。
课堂小结
畅谈收获:本节课你有哪些收获?
1、什么叫加减消元法?
2、加减消元法的步骤是什么?
分层演练
1. 用加减法解方程组
6x+7y=-19①
6x-5y=17②
应用( )
A.①-②消去y
B.①-②消去x
C. ②- ①消去常数项
D. 以上都不对
B
知识点拨:未知数x的系数相等,两个方程组相减即可消去x。
2.已知方程组 解为 ,则2a-3b的值为( )
A、4 B、6 C、-6 D、-4
ax-by=4
ax+by=2
x=2
y=1
B
知识点拨:将解分别带入方程组,问题就转化为一组关于a、b的二元一次方程组。
分层演练
3、若 ,则x+2y= ______
-3
1
-1
4.已知2ayb3x+1与-3ax-2b2-2y是同类项,则x = ,y=__ _
知识点拨:根据算术平方根和绝对值的非负性可得x+y+2=0,x-y=0.
知识点拨:所含字母形同,并且相同字母的指数也相同的项叫做同类项。
分层演练
分层演练
①
②
6、用较为简便的方法解方程组:
解:由① + ②,得 4(x+y)=36
所以 x+y=9 ③
由① - ②,得 6(x-y)=24
所以 x-y=4 ④
解由③④组成的方程组
解得
课后作业
课本教材第98页:3、4、5题
https://www.21cnjy.com/help/help_extract.php
人教版 七年级数学下
8.2加减消元法
---解二元一次方程组
学习目标
1.掌握加减消元法的意义;
2.会用加减法解二元一次方程组.(重点)
回顾旧知
10-x
2x+(10-x)=16
同学们观察,这两个方程中y的系数有什么关系?利用这种关系你能发现新的消元法吗?
x+y=10 ①
2x+y=16 ②
1.用代入法解二元一次方程组
解:由①得:y= ③
把③代入②得:
解得:x=6
将x=6代入③得:y=4
所以这个方程组的解是:
x=6
y=4
我们发现两个方程中y的系数相等,进而想到利用等式的性质将两个方程相减就可以消去y, ①- ②或②- ①都行,具体分析如下。
合作探究---加减消元法
1.用解二元一次方程组
①
②
分析: ②- ①
② 左边 - ①左边 = ②右边 - ① 右边
2x+y -x-y=6
x=6
(2x+y)
- (x+y)
= 16
-10
x+y=10 ①
2x+y=16 ②
1.解二元一次方程组:
合作探究---加减消元法
所以这个方程组的解是:
解:由②-①得: x=6
把x=6代入①得: 6+y=10
解得: y=4
方法总结:
同一未知数的系数
时,
把两个方程的两边分别 !
相等
相减
合作探究---加减消元法
3x +10 y=2.8 ①
15x -10 y=8 ②
解:把 ①+②得: 18x=10.8
x=0.6
把x=0.6代入①,得:
3×0.6+10y=2.8
解得:y=0.1
2、解方程组:
所以这个方程组的解是
x=0.6
y=0.1
同学们观察,这两个方程中y的系数有什么关系?
方程①、②中未知数y的系数互为相反数,可以利用两个方程相加消去未知数y.
方法总结:
同一未知数的系数
时,
把两个方程的两边分别 !
互为相反数
相加
将x=0.6代入②可以吗?
合作探究---加减消元法
归纳总结:
像上面这种解二元一次方程组的方法,叫做加减消元法,
简称加减法.
当方程组中两个方程的同一未知数的系数互为相反数或相等时,把这两个方程的两边分别相加(系数互为相反数)或相减(系数相等)来消去这个未知数,得到一个一元一次方程,进而求得二元一次方程组的解.
合作探究---加减消元法
3、用加减法解方程组:
①
②
①×3得:
所以原方程组的解是
解:
③-④得: y=2
把y=2代入①,
解得: x=3
②×2得:
6x+9y=36 ③
6x+8y=34 ④
同学们再观察,这两个方程中x、y的系数有什么关系?
方程①、②中未知数x、y的系数既不互为相反数,也不相等,所以不能直接通过加减来消元.
为了消元,我们可以在方程两边乘适当的数,使同一个未知数在两个方程中的系数相等或相反,比如我们对x的系数进行改造。
如果用加减法消去y,应如何解?解得结果一样吗?
方法总结:
同一未知数的系数
时,
我们可以通过等式的性质,
使未知数的系数
!
不相等也不互为相反数
相等或
互为相反数
小试牛刀
1、用加减法解下列方程组:
小试牛刀
2、已知 , 则a+b等于_____.
3
①
②
知识点拨:方法一:直接解方程组,求出a与b的值,然后就可以求出a+b.
方法二:?+?得 :4a+4b=12, a+b=3.
变式训练:已知x、y满足方程组 求代数式x-y的值.
解: ②-①得:2x-2y=-1-5,
得:x-y=-3.
总结归纳
变形后加减消元法解方程组的主要步骤有哪些?
变形
变同一个未知数的系数相同或互为相反数
加减
求解
写解
写出方程组的解
消去一个未知数化为一元一次方程
求出一个未知数的值
回代
代入原方程求出另一个未知数的解
消元先看相同未知数系数的最小公倍数
用加减法解决实际问题
分析:题目中存在的两个等量关系:
2×(2台大收割量+5台小收割量)=______
5×(3台大收割量+2台小收割量)=______
例4 2台大收割机和5台小收割机均工作2h共收割小麦3.6 hm2,3台大收割机和2台小收割机同时工作5h共收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
3.6hm2
8hm2
用加减法解决实际问题
解:设一台大收割机和一台小收割机每小时各收割小麦x hm2和y hm2.根据题意,得
②-①,得 ______
解得 x=_______
把x=_____ 代入①,得y=______
所以方程组的解为:
答:一台大收割机和一台小收割
机每小时分别收割小麦0.4hm2
和0.2hm2
11x=4.4
0.4
0.4
0.2
①
②
小试牛刀
1、某停车场的收费标准如下:中型汽车的停车费为12元/辆,小型汽车的停车费为8元/辆,现在停车场共有50辆中、小型汽车,这些车共缴纳停车费480元,中、小型汽车各有多少辆?
归纳总结
思考:我们现在已经学习了两种解二元一次方程组的方法,那么如何合理的选择消元法来解二元一次方程组?
(1)代入消元法:当存在未知数的系数的绝对值是1 的时候我们优先
选择代入法;
(2)加减消元法:当未知数的系数相等或者互为相反数又或者存在整
倍数关系时我们优先选择加减法。
课堂小结
畅谈收获:本节课你有哪些收获?
1、什么叫加减消元法?
2、加减消元法的步骤是什么?
分层演练
1. 用加减法解方程组
6x+7y=-19①
6x-5y=17②
应用( )
A.①-②消去y
B.①-②消去x
C. ②- ①消去常数项
D. 以上都不对
B
知识点拨:未知数x的系数相等,两个方程组相减即可消去x。
2.已知方程组 解为 ,则2a-3b的值为( )
A、4 B、6 C、-6 D、-4
ax-by=4
ax+by=2
x=2
y=1
B
知识点拨:将解分别带入方程组,问题就转化为一组关于a、b的二元一次方程组。
分层演练
3、若 ,则x+2y= ______
-3
1
-1
4.已知2ayb3x+1与-3ax-2b2-2y是同类项,则x = ,y=__ _
知识点拨:根据算术平方根和绝对值的非负性可得x+y+2=0,x-y=0.
知识点拨:所含字母形同,并且相同字母的指数也相同的项叫做同类项。
分层演练
分层演练
①
②
6、用较为简便的方法解方程组:
解:由① + ②,得 4(x+y)=36
所以 x+y=9 ③
由① - ②,得 6(x-y)=24
所以 x-y=4 ④
解由③④组成的方程组
解得
课后作业
课本教材第98页:3、4、5题
https://www.21cnjy.com/help/help_extract.php
