第九章 几何图形初步单元测试卷(含解析)
文档属性
| 名称 | 第九章 几何图形初步单元测试卷(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 504.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览




文档简介
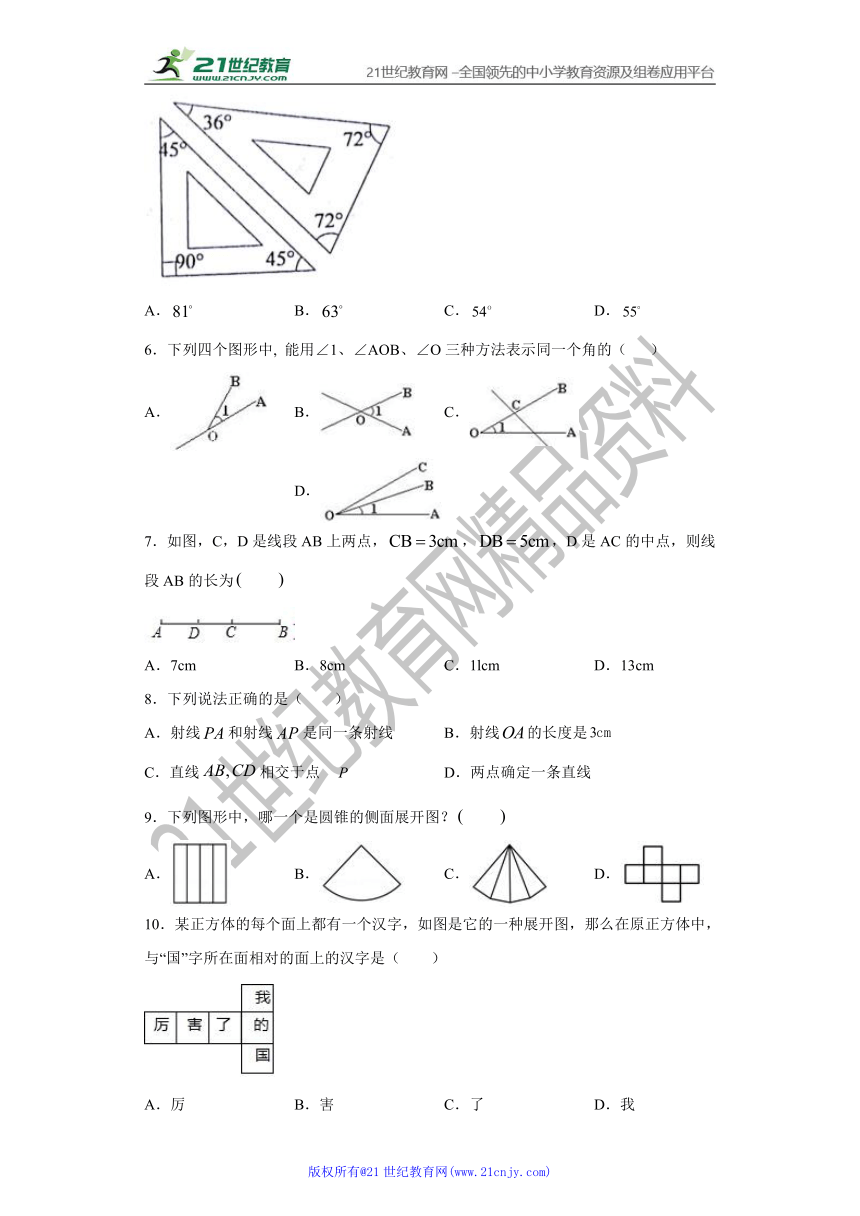
第九章几何图形初步单元测试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共10小题,满分30分,每小题3分)
1.下列语句正确的有(?? )
(1)线段AB就是 A、B两点间的距离;(2)画射线 AB=10cm;(3)A,B两点之间的所有连线中,线段AB最短;(4)在直线上取 A,B,C 三点,使得 AB=5cm,BC=2cm,则 AC=7cm.
A.1 个 B.2 个 C.3 个 D.4 个
2.把一根木条固定在墙面上,至少需要两枚钉子,这样做的数学依据是( )
A.两点之间线段最短 B.两点确定一条直线
C.垂线段最短 D.两点之间直线最短
3.如图,钟表上10点整时,时针与分针所成的角是( )
A. B. C. D.
4.如图,点C、O、B在同一条直线上,∠AOB=90°,∠AOE=∠DOB,则下列结论:①∠EOD=90°;②∠COE=∠AOD;③∠COE=∠DOB;④∠COE+∠BOD=90°.其中正确的个数是( )
A.1 B.2 C.3 D.4
5.如图,用一副特制的三角板可以画出一些特殊角.在下列选项中,不能画出的角度是( )
A. B. C. D.
6.下列四个图形中, 能用∠1、∠AOB、∠O三种方法表示同一个角的( )
A. B. C. D.
7.如图,C,D是线段AB上两点,,,D是AC的中点,则线段AB的长为
A.7cm B.8cm C.1lcm D.13cm
8.下列说法正确的是( )
A.射线和射线是同一条射线 B.射线的长度是
C.直线相交于点 D.两点确定一条直线
9.下列图形中,哪一个是圆锥的侧面展开图?
A. B. C. D.
10.某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“国”字所在面相对的面上的汉字是( )
A.厉 B.害 C.了 D.我
二、填空题(共7小题,满分28分,每小题4分)
11.有5个面的棱柱是______棱柱.
12.如图,AB=10cm,O为线段AB上的任意一点,C为AO的中点,D为OB的中点,则线段CD长_____.
13.计算, ________
14.线段AB=6,点C在直线AB上,BC=4,则AC的长度为________.
15.如图,线段,,则______用含a,b的式子表示
16.直线a上有5个不同的点A、B、C、D、E,则该直线上共有______ 条线段.
17.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是_____.
三、解答题(共6小题,满分42分,每题7分)
18.将图中的图形按要求分类:
(1)若按柱、锥、球划分;(2)若按组成面的曲或平划分.
19.如图,已知∠AOC=∠BOD=90°,∠COD=38°,求∠AOB的度数.
20.如图,是平角,, ,平分;
如图所示,图中小于平角的角有______个.
(1)求的度数;
(2)是的平分线吗?为什么?
21.用尺规作图按下列语句画图:
(1)画射线BC,连接AC,AB;
(2)反向延长线段AB至点D,使得DA=AB.
22.如图,延长AB至D,使B为AD的中点,点C在BD上,CD=2BC.
(1)AB= AD,AB﹣CD= ;
(2)若BC=3,求AD的长.
23.图1所示的三棱柱,高为8cm,底面是一个边长为5cm的等边三角形.
(1)这个三棱柱有 条棱,有 个面;
(2)图2框中的图形是该三棱柱的一种表面展开图的一部分,请将它补全(一种即可);
(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,至少需剪开 条棱,需剪开棱的棱长的和的最大值为 cm.
参考答案
1.A
【解析】
【分析】
根据线段和射线的定义进行分析、判断即可.
【详解】
(1)线段 AB的长度就是 A、B 两点间的距离;故(1)错误;
(2)线段的长度能够度量,而直线、射线的长度不能度量,故(2)错误;
(3)两点之间,线段最短,故(3)正确;
(4)因为C点的位置没有确定,所以AC的长度也不能确定,故(4)错误.
故答案选:A.
【点睛】
本题考查了两点间的距离及线段、射线的定义.解答该题时,需要熟练掌握它们的概念,才能做出正确的判断与选择.
2.B
【解析】因为两点确定一条直线,所以把一根木条固定在墙面上,至少需要两枚钉子故选B.
3.B
【解析】
【分析】
根据钟面分成12个大格,每格的度数为30°即可解答.
【详解】
解:∵钟面分成12个大格,每格的度数为30°,
∴钟表上10点整时,时针与分针所成的角是60°
故选:B.
【点睛】
考核知识点:钟面角.了解钟面特点是关键.
4.C
【解析】
∵∠AOB=90° ∴∠AOD+∠BOD=90° ∵∠AOE=∠DOB ∴∠AOE+∠AOD=90°,即∠EOD=90° ∴∠COE=∠AOD,∠COE+∠BOD=90° ∴①②④正确. 故选C.
【点睛】解题时注意运用余角的性质:同角的余角相等.
5.D
【解析】
【分析】
一副三角板中的度数,用三角板画出角,无非是用角度加减,逐一分析即可.
【详解】
解:A、,则角能画出;
B、,则角能画出;
C、,则可以画出;
D、55°不能写成36°、72°、45°、90°的和或差的形式,不能画出;
故选:D.
【点睛】
此题考查的知识点是角的计算,关键是用三角板直接画特殊角的步骤:先画一条射线,再把三角板所画角的一边与射线重合,顶点与射线端点重合,最后沿另一边画一条射线,标出角的度数.
6.C
【解析】
【分析】
根据角的三种表示方法,可得正确答案.
【详解】
A、∠O有歧义,故不是,与题意不符;
B、∠O有歧义,故不是,与题意不符;
C、∠1、∠AOB、∠O三种方法表示同一个角,故是,与题意相符;
D、∠O有歧义,故不是,与题意不符;
故选:C.
【点睛】
本题考查了角的概念,熟记角的表示方法是解题关键.在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角.
7.A
【解析】
【分析】
先根据,求出CD的长,再根据D是AC的中点得出AC的长,进而可得出结论.
【详解】
,,
,
是AC的中点,
,
.
故选:A.
【点睛】
本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.
8.D
【解析】
【分析】
根据直线、射线、线段的性质对各选项分析判断后利用排除法.
【详解】
解:A、射线PA和射线AP不是同一条射线,故本选项错误;
B、射线是无限长的,故本选项错误;
C、直线AB、CD可能平行,没有交点,故本选项错误;
D、两点确定一条直线是正确的.
故选:D.
【点睛】
本题主要考查了直线、射线、线段的特性,是基础题,需熟练掌握.
9.B
【解析】
【分析】
根据圆锥的侧面展开图的特点作答.
【详解】
A选项:是长方体展开图.
B选项:是圆锥展开图.
C选项:是棱锥展开图.
D选项:是正方体展开图.
故选B.
【点睛】
考查了几何体的展开图,注意圆锥的侧面展开图是扇形.
10.D
【解析】
分析:正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
详解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“的”与“害”是相对面,
“了”与“厉”是相对面,
“我”与“国”是相对面.
故选:D.
点睛:本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
11.三
【解析】
【分析】
去掉棱柱的上下底面知侧面有3个面,据此可得.
【详解】
解:有5个面的棱柱是三棱柱,
故答案为:三.
【点睛】
考查认识立体图形,解题的关键是掌握n棱柱有2n个顶点,有(n+2)个面,有3n条棱.
12.5cm.
【解析】
【分析】
依据C为AO的中点,D为OB的中点,即可得到
再根据AB=10cm,即可得到CD的长.
【详解】
∵C为AO的中点,D为OB的中点,
∴
∴
故答案为:5cm.
【点睛】
考查了两点间的距离,掌握中点的定义是解题的关键.
13.
【解析】
解:39′+31′=70′=1°10′,故48°39′+67°31′=116°10'.故答案为:116°10'.
14.2或10
【解析】点C在AB内,有AC=6-4=2,点C在AB右侧,AC=4+6=10.
故答案为2或10.
15.
【解析】
【分析】
观察图形可知AD+BC=AC+CD+BD+CD=AB+CD,再代入计算即可求解.
【详解】
∵AB=a,CD=b,∴AD+BC=AC+CD+BD+CD=AB+CD=a+b.
故答案为:a+b.
【点睛】
本题考查了两点间的距离,列代数式,关键是根据图形得到AD+BC=AB+CD.
16.10
【解析】
解:根据题意画图:
由图可知有AB、AC、AD、AE、BC、BD、BE、CD、CE、DE,共10条.故答案为:10.
17.两点之间线段最短
【解析】
田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,
能正确解释这一现象的数学知识是:两点之间线段最短,
故答案为:两点之间线段最短.
18.(1)柱:①③④⑤⑦;椎:②;球:⑥.(2)曲面:②⑥⑦;平面:①③④⑤.
【解析】
【分析】
(1)首先要明确柱、锥、球的概念,然后根据图示进行解答;
(2)观察图形是否有曲面进行解答.
【详解】
解:(1)柱:①③④⑤⑦;椎:②;球:⑥.
(2)曲面:②⑥⑦;平面:①③④⑤.
【点睛】
本题考查了立体图形的定义,注意几何体的分类,一般分为柱体、锥体、球,注意球和圆的区别,球是立体图形,圆是平面图形.
19.∠AOB=142°
【解析】
【分析】
先求出,代入,即可求出答案.
【详解】
解:,,
,
【点睛】
本题考查了角的计算及余角和补角的概念,熟悉图形是解题的关键.
20.(1)∠DOE=90°;(2)是,理由见解析.
【解析】
【分析】
(1)根据角平分线的定义,即可求出∠DOC,从而求出的度数;
(2)先求出∠AOE,然后根据平角的定义即可求出∠EOB,从而得出∠EOB=∠COE,根据角平分线的定义即可证出结论.
【详解】
解:(1)∠AOC=80°,OD平分∠AOC
∠AOD=∠DOC=40°,
∠COE=50°,
∠DOE=∠DOC +∠COE =40°+50°=90°
(2)是,理由如下
∠AOE=∠AOC+∠COE=80°+50°=130°,
∠EOB=180°-∠AOE=50°,
∠COE=50°,
∠EOB=∠COE,
OE是∠BOC的平分线.
【点睛】
此题考查的是角的和与差,掌握各个角的关系和角平分线的定义是解决此题的关键.
21.(1)见详解;(2)见详解.
【解析】
【分析】
(1)根据尺规作图过程画射线BC,连接AC,AB即可;
(2)根据尺规作图过程反向延长线段AB至点D,使得DA=AB即可.
【详解】
解:如图所示:
(1)(1)射线BC,连接AC,AB即为所求作的图形;
(2)如图所示即为所求作的图形.
【点睛】
本题考查了作图??复杂作图、直线、射线、线段,解决本题的关键是根据语句准确画图.
22.(1),BC;(2)答案见解析.
【解析】
【分析】
(1)根据线段中点的定义、线段的和差可得;(2)根据BC=3求出CD,根据线段中点定义求出AB,再根据AD=AB+BD即可解决问题.
【详解】
解:(1)因为B为AD的中点,
所以AB=BD=AD,
所以AB﹣CD=BD﹣CD=BC,
故答案为:,BC.
(2)因为BC=3,CD=2BC,
所以CD=2BC=6,
所以BD=BC+CD=3+6=9
因为B是AD中点,
∴AB=BD=9,
∴AD=AB+BD=9+9=18,
即AD的长是18.
【点睛】
本题考查两点间距离,线段的和差定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
23.(1)9,5;(2)见解析;(3)5,34
【解析】
【分析】
(1) n棱柱有n个侧面,2个庭面,3n条棱,2n个顶点;
(2)利用三棱柱及其表面展开图的特点解题;
(3)三棱柱有9条棱,观察三棱柱的展开图可知没有剪开的棱的条数星条,相减即可求出需要剪开的棱的条数;
【详解】
(1)这个三棱柱有条9棱,有个5面;故答家为:9,5;
(2)
(3)由图形可知:没有剪开的棱的条数是4条则至少需要剪开的棱的条数是:9﹣4=5(余)故至少需要开的楼的条数是5条,需开棱的棱长的和的最大值为:8×3+5×2=34(cm)
故答案为:5,34
【点睛】
本题主要考查的是认识立体图形,明确m棱柱有n个面,2个底面,3n条棱,2n个顶点;能够数出三棱柱没有开的棱的条数是解答此的关量
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共10小题,满分30分,每小题3分)
1.下列语句正确的有(?? )
(1)线段AB就是 A、B两点间的距离;(2)画射线 AB=10cm;(3)A,B两点之间的所有连线中,线段AB最短;(4)在直线上取 A,B,C 三点,使得 AB=5cm,BC=2cm,则 AC=7cm.
A.1 个 B.2 个 C.3 个 D.4 个
2.把一根木条固定在墙面上,至少需要两枚钉子,这样做的数学依据是( )
A.两点之间线段最短 B.两点确定一条直线
C.垂线段最短 D.两点之间直线最短
3.如图,钟表上10点整时,时针与分针所成的角是( )
A. B. C. D.
4.如图,点C、O、B在同一条直线上,∠AOB=90°,∠AOE=∠DOB,则下列结论:①∠EOD=90°;②∠COE=∠AOD;③∠COE=∠DOB;④∠COE+∠BOD=90°.其中正确的个数是( )
A.1 B.2 C.3 D.4
5.如图,用一副特制的三角板可以画出一些特殊角.在下列选项中,不能画出的角度是( )
A. B. C. D.
6.下列四个图形中, 能用∠1、∠AOB、∠O三种方法表示同一个角的( )
A. B. C. D.
7.如图,C,D是线段AB上两点,,,D是AC的中点,则线段AB的长为
A.7cm B.8cm C.1lcm D.13cm
8.下列说法正确的是( )
A.射线和射线是同一条射线 B.射线的长度是
C.直线相交于点 D.两点确定一条直线
9.下列图形中,哪一个是圆锥的侧面展开图?
A. B. C. D.
10.某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“国”字所在面相对的面上的汉字是( )
A.厉 B.害 C.了 D.我
二、填空题(共7小题,满分28分,每小题4分)
11.有5个面的棱柱是______棱柱.
12.如图,AB=10cm,O为线段AB上的任意一点,C为AO的中点,D为OB的中点,则线段CD长_____.
13.计算, ________
14.线段AB=6,点C在直线AB上,BC=4,则AC的长度为________.
15.如图,线段,,则______用含a,b的式子表示
16.直线a上有5个不同的点A、B、C、D、E,则该直线上共有______ 条线段.
17.如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是_____.
三、解答题(共6小题,满分42分,每题7分)
18.将图中的图形按要求分类:
(1)若按柱、锥、球划分;(2)若按组成面的曲或平划分.
19.如图,已知∠AOC=∠BOD=90°,∠COD=38°,求∠AOB的度数.
20.如图,是平角,, ,平分;
如图所示,图中小于平角的角有______个.
(1)求的度数;
(2)是的平分线吗?为什么?
21.用尺规作图按下列语句画图:
(1)画射线BC,连接AC,AB;
(2)反向延长线段AB至点D,使得DA=AB.
22.如图,延长AB至D,使B为AD的中点,点C在BD上,CD=2BC.
(1)AB= AD,AB﹣CD= ;
(2)若BC=3,求AD的长.
23.图1所示的三棱柱,高为8cm,底面是一个边长为5cm的等边三角形.
(1)这个三棱柱有 条棱,有 个面;
(2)图2框中的图形是该三棱柱的一种表面展开图的一部分,请将它补全(一种即可);
(3)要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,至少需剪开 条棱,需剪开棱的棱长的和的最大值为 cm.
参考答案
1.A
【解析】
【分析】
根据线段和射线的定义进行分析、判断即可.
【详解】
(1)线段 AB的长度就是 A、B 两点间的距离;故(1)错误;
(2)线段的长度能够度量,而直线、射线的长度不能度量,故(2)错误;
(3)两点之间,线段最短,故(3)正确;
(4)因为C点的位置没有确定,所以AC的长度也不能确定,故(4)错误.
故答案选:A.
【点睛】
本题考查了两点间的距离及线段、射线的定义.解答该题时,需要熟练掌握它们的概念,才能做出正确的判断与选择.
2.B
【解析】因为两点确定一条直线,所以把一根木条固定在墙面上,至少需要两枚钉子故选B.
3.B
【解析】
【分析】
根据钟面分成12个大格,每格的度数为30°即可解答.
【详解】
解:∵钟面分成12个大格,每格的度数为30°,
∴钟表上10点整时,时针与分针所成的角是60°
故选:B.
【点睛】
考核知识点:钟面角.了解钟面特点是关键.
4.C
【解析】
∵∠AOB=90° ∴∠AOD+∠BOD=90° ∵∠AOE=∠DOB ∴∠AOE+∠AOD=90°,即∠EOD=90° ∴∠COE=∠AOD,∠COE+∠BOD=90° ∴①②④正确. 故选C.
【点睛】解题时注意运用余角的性质:同角的余角相等.
5.D
【解析】
【分析】
一副三角板中的度数,用三角板画出角,无非是用角度加减,逐一分析即可.
【详解】
解:A、,则角能画出;
B、,则角能画出;
C、,则可以画出;
D、55°不能写成36°、72°、45°、90°的和或差的形式,不能画出;
故选:D.
【点睛】
此题考查的知识点是角的计算,关键是用三角板直接画特殊角的步骤:先画一条射线,再把三角板所画角的一边与射线重合,顶点与射线端点重合,最后沿另一边画一条射线,标出角的度数.
6.C
【解析】
【分析】
根据角的三种表示方法,可得正确答案.
【详解】
A、∠O有歧义,故不是,与题意不符;
B、∠O有歧义,故不是,与题意不符;
C、∠1、∠AOB、∠O三种方法表示同一个角,故是,与题意相符;
D、∠O有歧义,故不是,与题意不符;
故选:C.
【点睛】
本题考查了角的概念,熟记角的表示方法是解题关键.在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角.
7.A
【解析】
【分析】
先根据,求出CD的长,再根据D是AC的中点得出AC的长,进而可得出结论.
【详解】
,,
,
是AC的中点,
,
.
故选:A.
【点睛】
本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.
8.D
【解析】
【分析】
根据直线、射线、线段的性质对各选项分析判断后利用排除法.
【详解】
解:A、射线PA和射线AP不是同一条射线,故本选项错误;
B、射线是无限长的,故本选项错误;
C、直线AB、CD可能平行,没有交点,故本选项错误;
D、两点确定一条直线是正确的.
故选:D.
【点睛】
本题主要考查了直线、射线、线段的特性,是基础题,需熟练掌握.
9.B
【解析】
【分析】
根据圆锥的侧面展开图的特点作答.
【详解】
A选项:是长方体展开图.
B选项:是圆锥展开图.
C选项:是棱锥展开图.
D选项:是正方体展开图.
故选B.
【点睛】
考查了几何体的展开图,注意圆锥的侧面展开图是扇形.
10.D
【解析】
分析:正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
详解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“的”与“害”是相对面,
“了”与“厉”是相对面,
“我”与“国”是相对面.
故选:D.
点睛:本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
11.三
【解析】
【分析】
去掉棱柱的上下底面知侧面有3个面,据此可得.
【详解】
解:有5个面的棱柱是三棱柱,
故答案为:三.
【点睛】
考查认识立体图形,解题的关键是掌握n棱柱有2n个顶点,有(n+2)个面,有3n条棱.
12.5cm.
【解析】
【分析】
依据C为AO的中点,D为OB的中点,即可得到
再根据AB=10cm,即可得到CD的长.
【详解】
∵C为AO的中点,D为OB的中点,
∴
∴
故答案为:5cm.
【点睛】
考查了两点间的距离,掌握中点的定义是解题的关键.
13.
【解析】
解:39′+31′=70′=1°10′,故48°39′+67°31′=116°10'.故答案为:116°10'.
14.2或10
【解析】点C在AB内,有AC=6-4=2,点C在AB右侧,AC=4+6=10.
故答案为2或10.
15.
【解析】
【分析】
观察图形可知AD+BC=AC+CD+BD+CD=AB+CD,再代入计算即可求解.
【详解】
∵AB=a,CD=b,∴AD+BC=AC+CD+BD+CD=AB+CD=a+b.
故答案为:a+b.
【点睛】
本题考查了两点间的距离,列代数式,关键是根据图形得到AD+BC=AB+CD.
16.10
【解析】
解:根据题意画图:
由图可知有AB、AC、AD、AE、BC、BD、BE、CD、CE、DE,共10条.故答案为:10.
17.两点之间线段最短
【解析】
田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,
能正确解释这一现象的数学知识是:两点之间线段最短,
故答案为:两点之间线段最短.
18.(1)柱:①③④⑤⑦;椎:②;球:⑥.(2)曲面:②⑥⑦;平面:①③④⑤.
【解析】
【分析】
(1)首先要明确柱、锥、球的概念,然后根据图示进行解答;
(2)观察图形是否有曲面进行解答.
【详解】
解:(1)柱:①③④⑤⑦;椎:②;球:⑥.
(2)曲面:②⑥⑦;平面:①③④⑤.
【点睛】
本题考查了立体图形的定义,注意几何体的分类,一般分为柱体、锥体、球,注意球和圆的区别,球是立体图形,圆是平面图形.
19.∠AOB=142°
【解析】
【分析】
先求出,代入,即可求出答案.
【详解】
解:,,
,
【点睛】
本题考查了角的计算及余角和补角的概念,熟悉图形是解题的关键.
20.(1)∠DOE=90°;(2)是,理由见解析.
【解析】
【分析】
(1)根据角平分线的定义,即可求出∠DOC,从而求出的度数;
(2)先求出∠AOE,然后根据平角的定义即可求出∠EOB,从而得出∠EOB=∠COE,根据角平分线的定义即可证出结论.
【详解】
解:(1)∠AOC=80°,OD平分∠AOC
∠AOD=∠DOC=40°,
∠COE=50°,
∠DOE=∠DOC +∠COE =40°+50°=90°
(2)是,理由如下
∠AOE=∠AOC+∠COE=80°+50°=130°,
∠EOB=180°-∠AOE=50°,
∠COE=50°,
∠EOB=∠COE,
OE是∠BOC的平分线.
【点睛】
此题考查的是角的和与差,掌握各个角的关系和角平分线的定义是解决此题的关键.
21.(1)见详解;(2)见详解.
【解析】
【分析】
(1)根据尺规作图过程画射线BC,连接AC,AB即可;
(2)根据尺规作图过程反向延长线段AB至点D,使得DA=AB即可.
【详解】
解:如图所示:
(1)(1)射线BC,连接AC,AB即为所求作的图形;
(2)如图所示即为所求作的图形.
【点睛】
本题考查了作图??复杂作图、直线、射线、线段,解决本题的关键是根据语句准确画图.
22.(1),BC;(2)答案见解析.
【解析】
【分析】
(1)根据线段中点的定义、线段的和差可得;(2)根据BC=3求出CD,根据线段中点定义求出AB,再根据AD=AB+BD即可解决问题.
【详解】
解:(1)因为B为AD的中点,
所以AB=BD=AD,
所以AB﹣CD=BD﹣CD=BC,
故答案为:,BC.
(2)因为BC=3,CD=2BC,
所以CD=2BC=6,
所以BD=BC+CD=3+6=9
因为B是AD中点,
∴AB=BD=9,
∴AD=AB+BD=9+9=18,
即AD的长是18.
【点睛】
本题考查两点间距离,线段的和差定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
23.(1)9,5;(2)见解析;(3)5,34
【解析】
【分析】
(1) n棱柱有n个侧面,2个庭面,3n条棱,2n个顶点;
(2)利用三棱柱及其表面展开图的特点解题;
(3)三棱柱有9条棱,观察三棱柱的展开图可知没有剪开的棱的条数星条,相减即可求出需要剪开的棱的条数;
【详解】
(1)这个三棱柱有条9棱,有个5面;故答家为:9,5;
(2)
(3)由图形可知:没有剪开的棱的条数是4条则至少需要剪开的棱的条数是:9﹣4=5(余)故至少需要开的楼的条数是5条,需开棱的棱长的和的最大值为:8×3+5×2=34(cm)
故答案为:5,34
【点睛】
本题主要考查的是认识立体图形,明确m棱柱有n个面,2个底面,3n条棱,2n个顶点;能够数出三棱柱没有开的棱的条数是解答此的关量
