第十七章 三角形单元测试卷(含解析)
文档属性
| 名称 | 第十七章 三角形单元测试卷(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 515.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览



文档简介
第十七章三角形单元测试卷
学校:___________姓名:___________班级:___________考号:___________
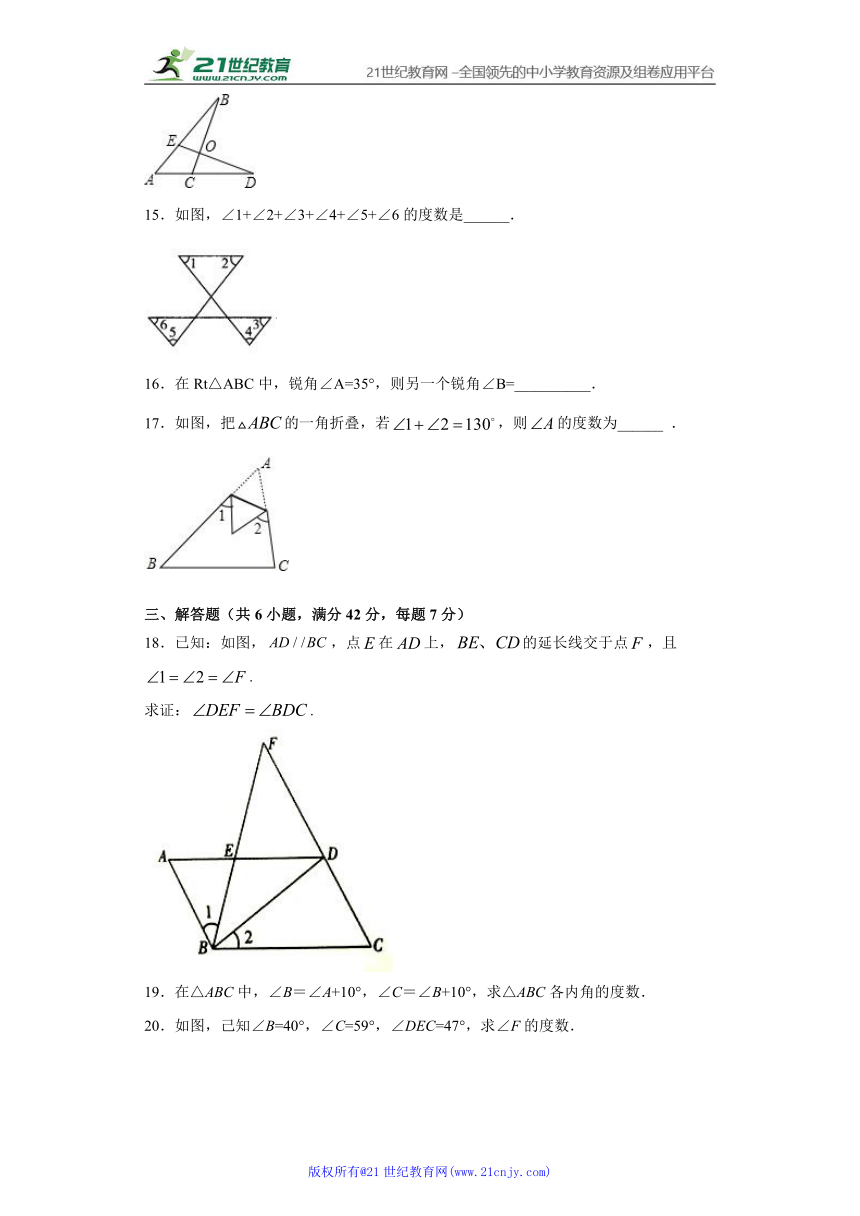
一、选择题(共10小题,满分30分,每小题3分)
1.小晶有两根长度为 5cm、8cm 的木条,她想钉一个三角形的木框,现在有长度分别为 2cm 、3cm、 8cm 、15cm 的木条供她选择,那她第三根应选择( )
A.2cm B.3cm C.8cm D.15cm
2.如图,一副三角板叠在一起,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,AC与DE交于点M,如果,则的度数为( )
A.80 B.85 C.90 D.95
3.如果一个多边形从一个顶点出发最多能画四条对角线,则这个多边形的边数为
A.5 B.6 C.7 D.8
4.若n边形的内角和等于外角和的3倍,则边数n为( )
A.n=6 B.n=7
C.n=8 D.n=9
5.在△ABC中,∠A==∠C,则这个三角形是( )
A.锐角三角形 B.等腰三角形
C.钝角三角形 D.含30°角的直角三角形
6.如图,点D在△ABC内,且∠BDC=120°,∠1+∠2=55°,则∠A的度数为( )
A.50° B.60° C.65° D.75°
7.一个多边形的内角和与它的外角和相等,这个多边形的边数是( )
A.3 B.4 C.5 D.6
8.如图,在中,平分,,且分别交,,及的延长线于点,,,,若,,则的度数为( )
A. B. C. D.
9.如图所示,∠的度数是( )
A.10° B.20° C.30° D.40°
10.如图AD⊥BC于点D,那么图中以AD为高的三角形有 个( )
A.3 B.4 C.5 D.6
二、填空题(共7小题,满分28分,每小题4分)
11.若正多边形的每一个内角为,则这个正多边形的边数是__________.
12.将一副三角板如图叠放,则图中∠α的度数为______.
13.从3cm、4cm、5cm、7cm的四根小棒中任取三根,能围成_____个三角形.
14.如图,于点,,,则____________.
15.如图,∠1+∠2+∠3+∠4+∠5+∠6的度数是______.
16.在Rt△ABC中,锐角∠A=35°,则另一个锐角∠B=__________.
17.如图,把的一角折叠,若,则的度数为______ .
三、解答题(共6小题,满分42分,每题7分)
18.已知:如图,,点在上,的延长线交于点,且.
求证:.
19.在△ABC中,∠B=∠A+10°,∠C=∠B+10°,求△ABC各内角的度数.
20.如图,己知∠B=40°,∠C=59°,∠DEC=47°,求∠F的度数.
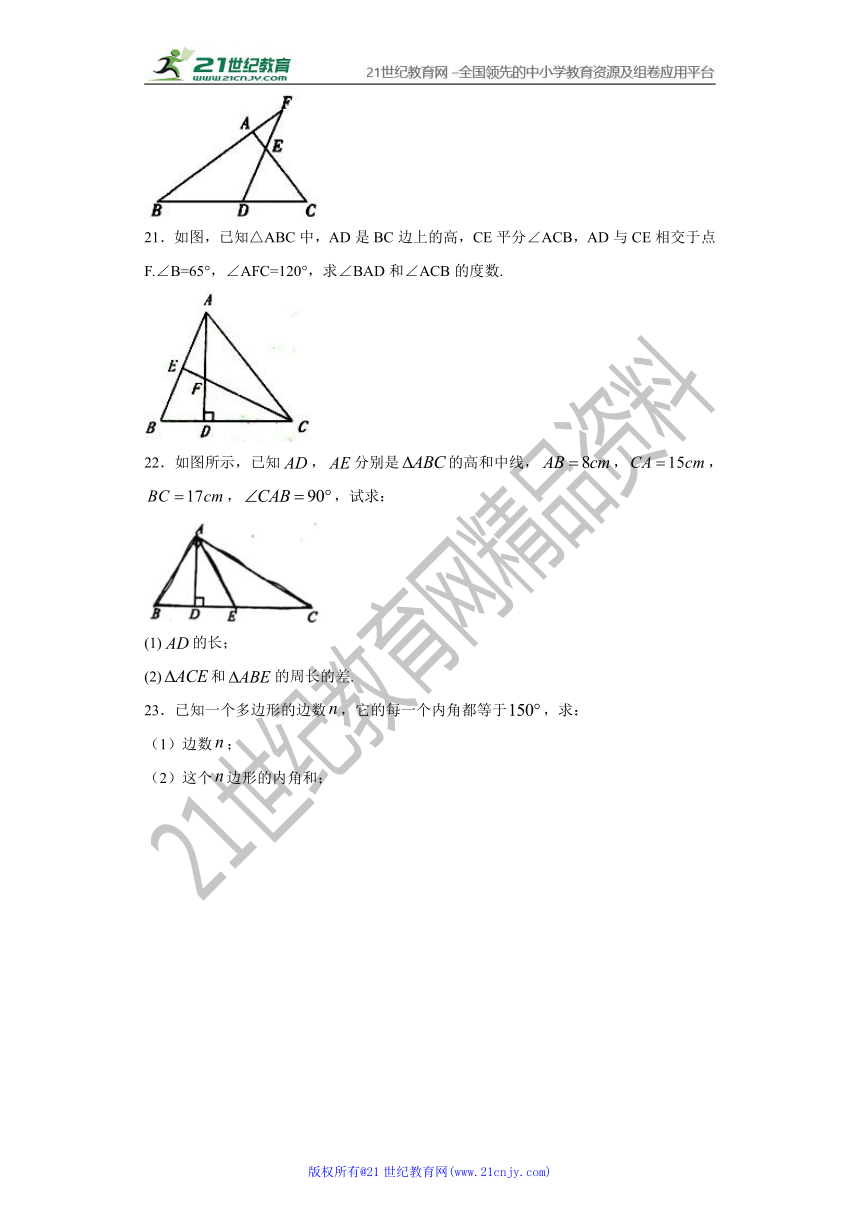
21.如图,已知△ABC中,AD是BC边上的高,CE平分∠ACB,AD与CE相交于点F.∠B=65°,∠AFC=120°,求∠BAD和∠ACB的度数.
22.如图所示,已知,分别是的高和中线,,,,,试求:
(1)的长;
(2)和的周长的差.
23.已知一个多边形的边数,它的每一个内角都等于,求:
(1)边数;
(2)这个边形的内角和;
参考答案
1.C
【解析】
【分析】
在三角形中,任意两边之和大于第三边,任意两边之差小于第三边.
【详解】
∵5+8=13,8-5=3
∴根据三角形三边关系,第三条边应在3cm~13cm之间(不包含3和13).
故选C
【点睛】
本题考查三角形三边关系,较为简单,熟练掌握三角形三边关系即可解题.
2.C
【解析】
【分析】
先根据平角的概念求出的度数,然后利用三角形内角和定理即可得出答案.
【详解】
故选:C.
【点睛】
本题主要考查三角形内角和定理及平角的概念,掌握三角形内角和定理是解题的关键.
3.C
【解析】
【分析】
根据从n边形的一个顶点可以作对角线的条数公式(n-3),求出边数即可.
【详解】
解:∵从一个多边形的一个顶点出发可以引4条对角线,设多边形边数为n,
∴n-3=4,
解得n=7.
故选:C.
【点睛】
本题考查了多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.熟知n边形从一个顶点出发可引出(n-3)条对角线是解题的关键.
4.C
【解析】
【分析】
根据n边形的内角和等于外角和的3倍,可得方程180(n-2)=360×3,再解方程即可.
【详解】
解:由题意得:180(n-2)=360×3, 解得:n=8, 故选:C.
【点睛】
此题主要考查了多边形内角和与外角和,要结合多边形的内角和公式与外角和的关系来寻求等量关系,构建方程即可求解.
5.D
【解析】
【分析】
先由∠A==∠C,可得∠B=2∠A,∠C=3∠A,再根据三角形的内角和是180°,列方程求得三个内角的度数,即可判断三角形的形状.
【详解】
解:∵∠A==∠C, ∴∠B=2∠A,∠C=3∠A, 又∵∠A+∠B+∠C=180°, ∴∠A+2∠A+3∠A=180°, ∴∠A=30°, ∴∠B=60°,∠C=90°, ∴△ABC是直角三角形. 故选D.
【点睛】
此题考查了三角形的内角和定理以及三角形的分类.解题关键在于利用内角和定理进行计算.
6.C
【解析】
【分析】
根据三角形的内角和即可求出.
【详解】
在△BCD中,∠BDC=120°,∴∠DBC+∠DCB=180°-∠BDC=60°,
∵∠1+∠2=55°,∴∠ABC+∠ACB=∠1+∠2+∠DBC+∠DCB=115°,
∴∠A=180°-(∠ABC+∠ACB)=65°.
故选C.
【点睛】
此题主要考查三角形的内角和,解题的关键是熟知三角形的内角和的性质.
7.B
【解析】
【分析】
根据多边形的内角和公式(n-2)?180°与多边形的外角和定理列式进行计算即可得解.
【详解】
设多边形的边数为n,根据题意得
(n-2)?180°=360°,
解得n=4.
故这个多边形是四边形.
故选B.
【点睛】
本题考查了多边形的内角和公式与外角和定理,熟记公式与定理是解题的关键.
8.A
【解析】
【分析】
根据三角形内角和及角平分线的定义可得∠DAC=30°,由可求出∠AFE的度数,根据对顶角相等可得∠GFC=∠AFE,利用外角性质求出∠G的度数即可.
【详解】
∵,,
∴∠BAC=180°-45°-75°=60°,
∵平分,
∴∠DAC=∠BAC=30°,
∵,
∴∠AFE=90°-∠DAC=60°,
∴∠GFC=∠AFE=60°,
∴∠G=∠ACB-∠GFC=75°-60°=15°,
故选:A.
【点睛】
本题考查三角形内角和定理及三角形外角的性质,任意三角形的内角和为180°;三角形的一个外角等于和它不相邻的两个内角的和;熟练掌握三角形内角和定理及外角性质是解题关键.
9.A
【解析】
如图:
∠1=30°+20°=40+∠,则∠=10°,
故选:A.
10.D
【解析】
结合三角形高的定义可知,以AD为高的三角形有:△ABD,△ABE,△ABC,△ADE,△ADC,△AEC,共6个.
故选:D.
11.八(或8)
【解析】
分析:根据正多边形的每一个内角为,求出正多边形的每一个外角,根据多边形的外角和,即可求出正多边形的边数.
详解:根据正多边形的每一个内角为,
正多边形的每一个外角为:
多边形的边数为:
故答案为八.
点睛:考查多边形的外角和,掌握多边形的外角和是解题的关键.
12.15°.
【解析】
解:由三角形的外角的性质可知,∠α=60°﹣45°=15°,故答案为:15°.
13.3
【解析】
【分析】
三角形三条边的特性:任意两边的长度和大于第三边,任意两边的长度差小于第三边.根据此特性,进行判断.
【详解】
解:3cm、4cm、5cm和7cm的四根木棒中,其中共有以下方案可组成三角形:
取3cm,4cm,5cm;由于5﹣3<4<5+3,能构成三角形;
取3cm,5cm,7cm;由于7﹣3<5<7+3,能构成三角形;
取4cm,5cm,7cm;由于7﹣4<5<7+4,能构成三角形.
所以有3种方法符合要求.
故答案为:3.
【点睛】
本题主要考查三角形三条边的关系:任意两边的长度和大于第三边,任意两边的长度差小于第三边.
14.20
【解析】
【分析】
已知∠A=50°,∠D=20°,根据三角形的一个外角等于与其不相邻的两内角和,可知∠BED=70°,又BC⊥ED于点O,根据直角三角形两锐角互余即可得出∠B的度数.
【详解】
根据题意,在△AED中,∠A=50°,∠D=20°,
∴∠BEO=∠A+∠D=70°,
∵BC⊥ED于点O,
∴∠BOE=90°,
∴∠B=90°-∠BEO=20°,
故答案为20°.
【点睛】
本题考查了三角形外角的性质以及直角三角形两锐角互余的性质,熟练掌握相关性质是解题的关键.
15.360°
【解析】
试题解析:由三角形外角性质得:∠8=∠1+∠2,∠7=∠3+∠4,∠9=∠6+∠5,
∴∠8+∠7+∠9=∠1+∠2+∠3+∠4+∠5+∠6,
∵△ABC的外角和等于360°,
∴∠1+∠2+∠3+∠4+∠5+∠6=∠7+∠8+∠9=360°.
点睛:本题考查了三角形外角和定理,三角形外角性质的应用,注意:三角形的外角和等于360°.
16.55°
【解析】
试题分析:∠B=90°-∠A=90°-35°=55°.
考点:直角三角形的两个锐角互余.
17.65°
【解析】
【分析】
根据折叠的性质得到∠3=∠5,∠4=∠6,利用平角的定义有∠3+∠5+∠1+∠2+∠4+∠6=360°,则2∠3+2∠4+∠1+∠2=360°,而∠1+∠2=130°,可计算出∠3+∠4=115°,然后根据三角形内角和定理即可得到∠A的度数.
【详解】
如图,∵△ABC的一角折叠,∴∠3=∠5,∠4=∠6,而∠3+∠5+∠1+∠2+∠4+∠6=360°,∴2∠3+2∠4+∠1+∠2=360°.
∵∠1+∠2=130°,∴∠3+∠4=115°,∴∠A=180°﹣∠3﹣∠4=65°.
故答案为:65°.
【点睛】
本题考查了三角形的内角和定理:三角形的内角和为180°.也考查了折叠的性质.作出辅助线,把图形补充完整是解题的关键.
18.见详解.
【解析】
【分析】
由平行线的性质及三角形外角的性质可证结论.
【详解】
解:
是的一个外角
是的一个外角
【点睛】
本题考查了平行线的性质及三角形外角的性质,灵活利用三角形的一个外角等于与它不相邻的两个内角和是解题的关键.
19.∠A=50°,∠B=60°,∠C=70°.
【解析】
【分析】
根据三角形的内角和定理,结合已知条件解方程即可.
【详解】
∵∠B=∠A+10°,∠C=∠B+10°,
又∵∠A+∠B+∠C=180°,
∴∠A+(∠A+10°)+(∠A+10°+10°)=180°,
3∠A+30°=180°,
3∠A=150°,
∠A=50°.
∴∠B=60°,∠C=70°.
【点睛】
此题主要考查利用三角形内角和定理,列出方程,即可解题.
20.∠F=34°.
【解析】
【分析】
先由外角的性质求∠CAF的度数,再利用对顶角相等得∠AEF的度数,最后运用三角形内角和定理求得∠F的度数.
【详解】
解:∵∠CAF=∠B+∠C=99°, 又∵∠AEF=∠DEC=47°(对顶角相等), ∴在△AEF中,∠F=180°-∠CAF-∠AEF=180°-99°-47°=34°.
【点睛】
本题考查三角形外角的性质及三角形的内角和定理,解题的关键是利用外角和内角的关系.
21.∠BAD的度数是25°,∠ACB的度数是60°
【解析】
【分析】
在△ABD中根据∠B和∠ADB的度数即可求出∠BAD的度数;根据外角性质可得∠FCD的度数,利用角平分线的性质即可得出∠ACB的度数.
【详解】
解:∵AD是BC边上的高
∴∠ADB=90°
在Rt△ABD中,∠BAD=90°-∠B=90°-65°=25°
∠AFC是ΔCDF的外角
即∠AFC=∠FDC+∠FCD
∴∠FCD=∠AFC-∠FDC=120°-90°=30°
∴CE平分∠ACB
∴∠ACB=2∠FCD=2×30°=60°
答:∠BAD的度数是25°,∠ACB的度数是60°.
【点睛】
本题考查的是三角形,需要熟练掌握三角形的相关性质与定理.
22.(1)长为;(2)周长差.
【解析】
【分析】
(1)利用直角三角形的面积法求线段AD的长度; (2)由于AE是中线,那么BE=CE,再表示△ACE的周长和△ABE的周长,化简可得△ACE的周长-△ABE的周长=AC-AB,即可求解.
【详解】
解:(1)∵∠BAC=90°,AD是边BC上的高, ∴S△ACB=AB?AC=BC?AD, ∵,,, ∴AD=8×15÷17= (cm), 即AD的长度为cm; (2)∵AE为BC边上的中线, ∴BE=CE, ∴△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=15-8=7(cm), 即△ACE和△ABE的周长的差是7cm.
【点睛】
本题考查中线的定义、三角形的面积,三角形周长的计算,解题的关键是利用三角形面积的两个表达式相等,求出AD.
23.(1)12;(2)1800o
【解析】
【分析】
(1) 先求出这个多边形的每一个外角的度数,再用360°除以一个外角的度数即可得到边数;
(2)根据内角和公式求解.
【详解】
(1)∵它的每一个内角都等于150o,
∴每个外角都等于30o,
∴n=;
(2)内角和为:
【点睛】
考查了多边形的内角与外角的关系,求出每一个外角的度数是关键.
学校:___________姓名:___________班级:___________考号:___________
一、选择题(共10小题,满分30分,每小题3分)
1.小晶有两根长度为 5cm、8cm 的木条,她想钉一个三角形的木框,现在有长度分别为 2cm 、3cm、 8cm 、15cm 的木条供她选择,那她第三根应选择( )
A.2cm B.3cm C.8cm D.15cm
2.如图,一副三角板叠在一起,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,AC与DE交于点M,如果,则的度数为( )
A.80 B.85 C.90 D.95
3.如果一个多边形从一个顶点出发最多能画四条对角线,则这个多边形的边数为
A.5 B.6 C.7 D.8
4.若n边形的内角和等于外角和的3倍,则边数n为( )
A.n=6 B.n=7
C.n=8 D.n=9
5.在△ABC中,∠A==∠C,则这个三角形是( )
A.锐角三角形 B.等腰三角形
C.钝角三角形 D.含30°角的直角三角形
6.如图,点D在△ABC内,且∠BDC=120°,∠1+∠2=55°,则∠A的度数为( )
A.50° B.60° C.65° D.75°
7.一个多边形的内角和与它的外角和相等,这个多边形的边数是( )
A.3 B.4 C.5 D.6
8.如图,在中,平分,,且分别交,,及的延长线于点,,,,若,,则的度数为( )
A. B. C. D.
9.如图所示,∠的度数是( )
A.10° B.20° C.30° D.40°
10.如图AD⊥BC于点D,那么图中以AD为高的三角形有 个( )
A.3 B.4 C.5 D.6
二、填空题(共7小题,满分28分,每小题4分)
11.若正多边形的每一个内角为,则这个正多边形的边数是__________.
12.将一副三角板如图叠放,则图中∠α的度数为______.
13.从3cm、4cm、5cm、7cm的四根小棒中任取三根,能围成_____个三角形.
14.如图,于点,,,则____________.
15.如图,∠1+∠2+∠3+∠4+∠5+∠6的度数是______.
16.在Rt△ABC中,锐角∠A=35°,则另一个锐角∠B=__________.
17.如图,把的一角折叠,若,则的度数为______ .
三、解答题(共6小题,满分42分,每题7分)
18.已知:如图,,点在上,的延长线交于点,且.
求证:.
19.在△ABC中,∠B=∠A+10°,∠C=∠B+10°,求△ABC各内角的度数.
20.如图,己知∠B=40°,∠C=59°,∠DEC=47°,求∠F的度数.
21.如图,已知△ABC中,AD是BC边上的高,CE平分∠ACB,AD与CE相交于点F.∠B=65°,∠AFC=120°,求∠BAD和∠ACB的度数.
22.如图所示,已知,分别是的高和中线,,,,,试求:
(1)的长;
(2)和的周长的差.
23.已知一个多边形的边数,它的每一个内角都等于,求:
(1)边数;
(2)这个边形的内角和;
参考答案
1.C
【解析】
【分析】
在三角形中,任意两边之和大于第三边,任意两边之差小于第三边.
【详解】
∵5+8=13,8-5=3
∴根据三角形三边关系,第三条边应在3cm~13cm之间(不包含3和13).
故选C
【点睛】
本题考查三角形三边关系,较为简单,熟练掌握三角形三边关系即可解题.
2.C
【解析】
【分析】
先根据平角的概念求出的度数,然后利用三角形内角和定理即可得出答案.
【详解】
故选:C.
【点睛】
本题主要考查三角形内角和定理及平角的概念,掌握三角形内角和定理是解题的关键.
3.C
【解析】
【分析】
根据从n边形的一个顶点可以作对角线的条数公式(n-3),求出边数即可.
【详解】
解:∵从一个多边形的一个顶点出发可以引4条对角线,设多边形边数为n,
∴n-3=4,
解得n=7.
故选:C.
【点睛】
本题考查了多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.熟知n边形从一个顶点出发可引出(n-3)条对角线是解题的关键.
4.C
【解析】
【分析】
根据n边形的内角和等于外角和的3倍,可得方程180(n-2)=360×3,再解方程即可.
【详解】
解:由题意得:180(n-2)=360×3, 解得:n=8, 故选:C.
【点睛】
此题主要考查了多边形内角和与外角和,要结合多边形的内角和公式与外角和的关系来寻求等量关系,构建方程即可求解.
5.D
【解析】
【分析】
先由∠A==∠C,可得∠B=2∠A,∠C=3∠A,再根据三角形的内角和是180°,列方程求得三个内角的度数,即可判断三角形的形状.
【详解】
解:∵∠A==∠C, ∴∠B=2∠A,∠C=3∠A, 又∵∠A+∠B+∠C=180°, ∴∠A+2∠A+3∠A=180°, ∴∠A=30°, ∴∠B=60°,∠C=90°, ∴△ABC是直角三角形. 故选D.
【点睛】
此题考查了三角形的内角和定理以及三角形的分类.解题关键在于利用内角和定理进行计算.
6.C
【解析】
【分析】
根据三角形的内角和即可求出.
【详解】
在△BCD中,∠BDC=120°,∴∠DBC+∠DCB=180°-∠BDC=60°,
∵∠1+∠2=55°,∴∠ABC+∠ACB=∠1+∠2+∠DBC+∠DCB=115°,
∴∠A=180°-(∠ABC+∠ACB)=65°.
故选C.
【点睛】
此题主要考查三角形的内角和,解题的关键是熟知三角形的内角和的性质.
7.B
【解析】
【分析】
根据多边形的内角和公式(n-2)?180°与多边形的外角和定理列式进行计算即可得解.
【详解】
设多边形的边数为n,根据题意得
(n-2)?180°=360°,
解得n=4.
故这个多边形是四边形.
故选B.
【点睛】
本题考查了多边形的内角和公式与外角和定理,熟记公式与定理是解题的关键.
8.A
【解析】
【分析】
根据三角形内角和及角平分线的定义可得∠DAC=30°,由可求出∠AFE的度数,根据对顶角相等可得∠GFC=∠AFE,利用外角性质求出∠G的度数即可.
【详解】
∵,,
∴∠BAC=180°-45°-75°=60°,
∵平分,
∴∠DAC=∠BAC=30°,
∵,
∴∠AFE=90°-∠DAC=60°,
∴∠GFC=∠AFE=60°,
∴∠G=∠ACB-∠GFC=75°-60°=15°,
故选:A.
【点睛】
本题考查三角形内角和定理及三角形外角的性质,任意三角形的内角和为180°;三角形的一个外角等于和它不相邻的两个内角的和;熟练掌握三角形内角和定理及外角性质是解题关键.
9.A
【解析】
如图:
∠1=30°+20°=40+∠,则∠=10°,
故选:A.
10.D
【解析】
结合三角形高的定义可知,以AD为高的三角形有:△ABD,△ABE,△ABC,△ADE,△ADC,△AEC,共6个.
故选:D.
11.八(或8)
【解析】
分析:根据正多边形的每一个内角为,求出正多边形的每一个外角,根据多边形的外角和,即可求出正多边形的边数.
详解:根据正多边形的每一个内角为,
正多边形的每一个外角为:
多边形的边数为:
故答案为八.
点睛:考查多边形的外角和,掌握多边形的外角和是解题的关键.
12.15°.
【解析】
解:由三角形的外角的性质可知,∠α=60°﹣45°=15°,故答案为:15°.
13.3
【解析】
【分析】
三角形三条边的特性:任意两边的长度和大于第三边,任意两边的长度差小于第三边.根据此特性,进行判断.
【详解】
解:3cm、4cm、5cm和7cm的四根木棒中,其中共有以下方案可组成三角形:
取3cm,4cm,5cm;由于5﹣3<4<5+3,能构成三角形;
取3cm,5cm,7cm;由于7﹣3<5<7+3,能构成三角形;
取4cm,5cm,7cm;由于7﹣4<5<7+4,能构成三角形.
所以有3种方法符合要求.
故答案为:3.
【点睛】
本题主要考查三角形三条边的关系:任意两边的长度和大于第三边,任意两边的长度差小于第三边.
14.20
【解析】
【分析】
已知∠A=50°,∠D=20°,根据三角形的一个外角等于与其不相邻的两内角和,可知∠BED=70°,又BC⊥ED于点O,根据直角三角形两锐角互余即可得出∠B的度数.
【详解】
根据题意,在△AED中,∠A=50°,∠D=20°,
∴∠BEO=∠A+∠D=70°,
∵BC⊥ED于点O,
∴∠BOE=90°,
∴∠B=90°-∠BEO=20°,
故答案为20°.
【点睛】
本题考查了三角形外角的性质以及直角三角形两锐角互余的性质,熟练掌握相关性质是解题的关键.
15.360°
【解析】
试题解析:由三角形外角性质得:∠8=∠1+∠2,∠7=∠3+∠4,∠9=∠6+∠5,
∴∠8+∠7+∠9=∠1+∠2+∠3+∠4+∠5+∠6,
∵△ABC的外角和等于360°,
∴∠1+∠2+∠3+∠4+∠5+∠6=∠7+∠8+∠9=360°.
点睛:本题考查了三角形外角和定理,三角形外角性质的应用,注意:三角形的外角和等于360°.
16.55°
【解析】
试题分析:∠B=90°-∠A=90°-35°=55°.
考点:直角三角形的两个锐角互余.
17.65°
【解析】
【分析】
根据折叠的性质得到∠3=∠5,∠4=∠6,利用平角的定义有∠3+∠5+∠1+∠2+∠4+∠6=360°,则2∠3+2∠4+∠1+∠2=360°,而∠1+∠2=130°,可计算出∠3+∠4=115°,然后根据三角形内角和定理即可得到∠A的度数.
【详解】
如图,∵△ABC的一角折叠,∴∠3=∠5,∠4=∠6,而∠3+∠5+∠1+∠2+∠4+∠6=360°,∴2∠3+2∠4+∠1+∠2=360°.
∵∠1+∠2=130°,∴∠3+∠4=115°,∴∠A=180°﹣∠3﹣∠4=65°.
故答案为:65°.
【点睛】
本题考查了三角形的内角和定理:三角形的内角和为180°.也考查了折叠的性质.作出辅助线,把图形补充完整是解题的关键.
18.见详解.
【解析】
【分析】
由平行线的性质及三角形外角的性质可证结论.
【详解】
解:
是的一个外角
是的一个外角
【点睛】
本题考查了平行线的性质及三角形外角的性质,灵活利用三角形的一个外角等于与它不相邻的两个内角和是解题的关键.
19.∠A=50°,∠B=60°,∠C=70°.
【解析】
【分析】
根据三角形的内角和定理,结合已知条件解方程即可.
【详解】
∵∠B=∠A+10°,∠C=∠B+10°,
又∵∠A+∠B+∠C=180°,
∴∠A+(∠A+10°)+(∠A+10°+10°)=180°,
3∠A+30°=180°,
3∠A=150°,
∠A=50°.
∴∠B=60°,∠C=70°.
【点睛】
此题主要考查利用三角形内角和定理,列出方程,即可解题.
20.∠F=34°.
【解析】
【分析】
先由外角的性质求∠CAF的度数,再利用对顶角相等得∠AEF的度数,最后运用三角形内角和定理求得∠F的度数.
【详解】
解:∵∠CAF=∠B+∠C=99°, 又∵∠AEF=∠DEC=47°(对顶角相等), ∴在△AEF中,∠F=180°-∠CAF-∠AEF=180°-99°-47°=34°.
【点睛】
本题考查三角形外角的性质及三角形的内角和定理,解题的关键是利用外角和内角的关系.
21.∠BAD的度数是25°,∠ACB的度数是60°
【解析】
【分析】
在△ABD中根据∠B和∠ADB的度数即可求出∠BAD的度数;根据外角性质可得∠FCD的度数,利用角平分线的性质即可得出∠ACB的度数.
【详解】
解:∵AD是BC边上的高
∴∠ADB=90°
在Rt△ABD中,∠BAD=90°-∠B=90°-65°=25°
∠AFC是ΔCDF的外角
即∠AFC=∠FDC+∠FCD
∴∠FCD=∠AFC-∠FDC=120°-90°=30°
∴CE平分∠ACB
∴∠ACB=2∠FCD=2×30°=60°
答:∠BAD的度数是25°,∠ACB的度数是60°.
【点睛】
本题考查的是三角形,需要熟练掌握三角形的相关性质与定理.
22.(1)长为;(2)周长差.
【解析】
【分析】
(1)利用直角三角形的面积法求线段AD的长度; (2)由于AE是中线,那么BE=CE,再表示△ACE的周长和△ABE的周长,化简可得△ACE的周长-△ABE的周长=AC-AB,即可求解.
【详解】
解:(1)∵∠BAC=90°,AD是边BC上的高, ∴S△ACB=AB?AC=BC?AD, ∵,,, ∴AD=8×15÷17= (cm), 即AD的长度为cm; (2)∵AE为BC边上的中线, ∴BE=CE, ∴△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=15-8=7(cm), 即△ACE和△ABE的周长的差是7cm.
【点睛】
本题考查中线的定义、三角形的面积,三角形周长的计算,解题的关键是利用三角形面积的两个表达式相等,求出AD.
23.(1)12;(2)1800o
【解析】
【分析】
(1) 先求出这个多边形的每一个外角的度数,再用360°除以一个外角的度数即可得到边数;
(2)根据内角和公式求解.
【详解】
(1)∵它的每一个内角都等于150o,
∴每个外角都等于30o,
∴n=;
(2)内角和为:
【点睛】
考查了多边形的内角与外角的关系,求出每一个外角的度数是关键.
