沪科版九年级数学下册24.6 正多边形的性质课件(共16张PPT)
文档属性
| 名称 | 沪科版九年级数学下册24.6 正多边形的性质课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 447.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
第2课时
正多边形的性质
思 考
将一个圆n等分,就可以作出这个圆的内接或外切正n边形,反过来,是不是每个正多边形都有一个外接圆和一个内切圆呢?
我们仍然以五边形为例来进行研究.
如图,过正五边形ABCDE的顶点A,B,C作⊙O,连结OA,OB,OC,OD,OE.
∵ OB=OC,
∴ ∠OBC=∠OCB.
又 ∵ ∠ABC=∠BCD,
∴ ∠OBA=∠OCD.
A
B
C
D
E
O
新课推进
∵ AB=DC,
∴ △OAB≌△ODC.
∴ OA=OD,
即点D在⊙O上.
同理,得点E也在⊙O上.
所以正五边形ABCDE有一个以O为圆心的外接圆.
A
B
C
D
E
O
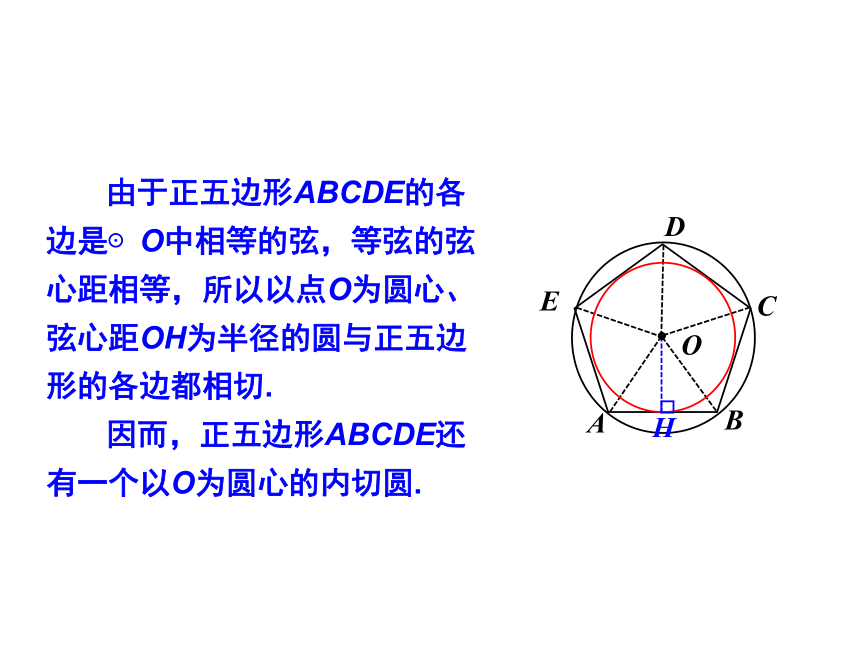
由于正五边形ABCDE的各边是⊙O中相等的弦,等弦的弦心距相等,所以以点O为圆心、弦心距OH为半径的圆与正五边形的各边都相切.
因而,正五边形ABCDE还有一个以O为圆心的内切圆.
A
B
C
D
E
O
H
任何正多边形都有一个外接圆和一个内切圆,并且这两个圆是同心圆.
正多边形的有关概念及相关计算
.
O
中心角
半径R
边心距r
正多边形的中心:该正多边形的外接圆和内切圆的公共圆心.
正多边形的半径:外接圆的半径.
正多边形的中心角:正多边形的每一条边所对的圆心角.
正多边形的边心距:内切圆的半径.
A
B
正n边形的一个内角的
度数是____________;
中心角是___________;
正多边形的中心角与外角的
大小关系是________.
相等
想一想:
正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心.
如果一个正多边形有偶数条边,那么它又是中心对称图形,它的中心就是对称中心.
例 求边长为a的正六边形的周长和面积.
解 如图,过正六边形的中心O作OG⊥BC,垂足是G,连接OB,OC,设该正六边形的周长和面积分别为C和S.
∵ 多边形ABCDEF是正六边形,
∴ ∠BOC=60°,△BOC是等边三角形.
∴ C=6BC=6a.
A
B
C
D
E
F
O
G
在△BOC中,有
1. 如图,要拧开一个边长为a=6mm的正六边形螺帽,扳手张开的开口b至少为多少?
解:如图,∠ABC=120°. AB=BC=a, AC=b.
过B作BD⊥AC于点D,
则AD=DC= b.
在Rt△ABD中,∠BAC=30°,
∴BD= AB=3mm.
∴b=2AD=6 mm.
即扳手张开的开口b至少要6 mm.
2. 求出半径为R的圆内接正三角形的边长,边心距和面积.
解:作等边△ABC的BC边上的高AD,垂足为D
·
A
B
C
D
O
连接OB,则OB=R
在Rt△OBD中∠OBD=30°,
边心距=OD=
在Rt△ABD中∠BAD=30°,
·
A
B
C
D
O
第2课时
正多边形的性质
思 考
将一个圆n等分,就可以作出这个圆的内接或外切正n边形,反过来,是不是每个正多边形都有一个外接圆和一个内切圆呢?
我们仍然以五边形为例来进行研究.
如图,过正五边形ABCDE的顶点A,B,C作⊙O,连结OA,OB,OC,OD,OE.
∵ OB=OC,
∴ ∠OBC=∠OCB.
又 ∵ ∠ABC=∠BCD,
∴ ∠OBA=∠OCD.
A
B
C
D
E
O
新课推进
∵ AB=DC,
∴ △OAB≌△ODC.
∴ OA=OD,
即点D在⊙O上.
同理,得点E也在⊙O上.
所以正五边形ABCDE有一个以O为圆心的外接圆.
A
B
C
D
E
O
由于正五边形ABCDE的各边是⊙O中相等的弦,等弦的弦心距相等,所以以点O为圆心、弦心距OH为半径的圆与正五边形的各边都相切.
因而,正五边形ABCDE还有一个以O为圆心的内切圆.
A
B
C
D
E
O
H
任何正多边形都有一个外接圆和一个内切圆,并且这两个圆是同心圆.
正多边形的有关概念及相关计算
.
O
中心角
半径R
边心距r
正多边形的中心:该正多边形的外接圆和内切圆的公共圆心.
正多边形的半径:外接圆的半径.
正多边形的中心角:正多边形的每一条边所对的圆心角.
正多边形的边心距:内切圆的半径.
A
B
正n边形的一个内角的
度数是____________;
中心角是___________;
正多边形的中心角与外角的
大小关系是________.
相等
想一想:
正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都通过n边形的中心.
如果一个正多边形有偶数条边,那么它又是中心对称图形,它的中心就是对称中心.
例 求边长为a的正六边形的周长和面积.
解 如图,过正六边形的中心O作OG⊥BC,垂足是G,连接OB,OC,设该正六边形的周长和面积分别为C和S.
∵ 多边形ABCDEF是正六边形,
∴ ∠BOC=60°,△BOC是等边三角形.
∴ C=6BC=6a.
A
B
C
D
E
F
O
G
在△BOC中,有
1. 如图,要拧开一个边长为a=6mm的正六边形螺帽,扳手张开的开口b至少为多少?
解:如图,∠ABC=120°. AB=BC=a, AC=b.
过B作BD⊥AC于点D,
则AD=DC= b.
在Rt△ABD中,∠BAC=30°,
∴BD= AB=3mm.
∴b=2AD=6 mm.
即扳手张开的开口b至少要6 mm.
2. 求出半径为R的圆内接正三角形的边长,边心距和面积.
解:作等边△ABC的BC边上的高AD,垂足为D
·
A
B
C
D
O
连接OB,则OB=R
在Rt△OBD中∠OBD=30°,
边心距=OD=
在Rt△ABD中∠BAD=30°,
·
A
B
C
D
O
