8.3.1 完全平方公式(要点测评+课后集训+答案)
文档属性
| 名称 | 8.3.1 完全平方公式(要点测评+课后集训+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览


文档简介
沪科版数学七年级下册同步课时训练
第8章 整式乘法与因式分解
8.3 完全平方公式与平方差公式
第1课时 完全平方公式
要点测评 基础达标
要点1 完全平方公式
1. 若4a2+kab+9b2是完全平方式,则常数k的值为( )
A. 6 B. 12 C. ±6 D. ±12
2. 下列各式中,与(-a+1)2相等的是( )
A. a2-1 B. a2+1 C. a2-2a+1 D. a2+2a+1
3. 计算:
(1)(4a+b)2; (2)(-2m-1)2.
要点2 完全平方公式的应用
4. 若a+b=3,a2+b2=7,则ab等于( )
A. 2 B. 1 C. -2 D. -1
5. 已知a+b=2,ab=1,求(a-b)2的值.
6. 运用公式简便计算:
(1)1032; (2)1982.
7. 先化简,再求值:(x+2)2+x(2-x),其中x=.
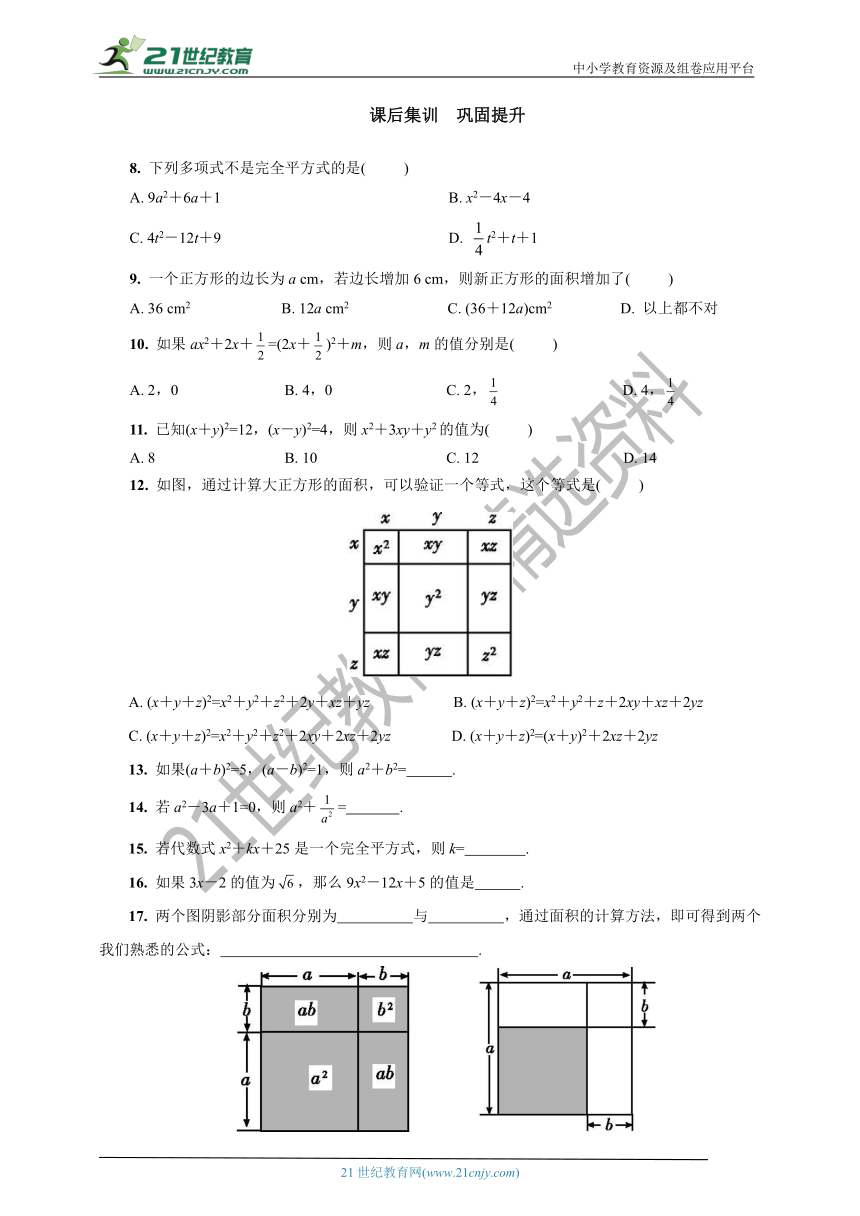
课后集训 巩固提升
8. 下列多项式不是完全平方式的是( )
A. 9a2+6a+1 B. x2-4x-4
C. 4t2-12t+9 D. t2+t+1
9. 一个正方形的边长为a cm,若边长增加6 cm,则新正方形的面积增加了( )
A. 36 cm2 B. 12a cm2 C. (36+12a)cm2 D. 以上都不对
10. 如果ax2+2x+=(2x+)2+m,则a,m的值分别是( )
A. 2,0 B. 4,0 C. 2, D. 4,
11. 已知(x+y)2=12,(x-y)2=4,则x2+3xy+y2的值为( )
A. 8 B. 10 C. 12 D. 14
12. 如图,通过计算大正方形的面积,可以验证一个等式,这个等式是( )
A. (x+y+z)2=x2+y2+z2+2y+xz+yz B. (x+y+z)2=x2+y2+z+2xy+xz+2yz
C. (x+y+z)2=x2+y2+z2+2xy+2xz+2yz D. (x+y+z)2=(x+y)2+2xz+2yz
13. 如果(a+b)2=5,(a-b)2=1,则a2+b2= .?
14. 若a2-3a+1=0,则a2+= .?
15. 若代数式x2+kx+25是一个完全平方式,则k= .
16. 如果3x-2的值为,那么9x2-12x+5的值是 .?
17. 两个图阴影部分面积分别为 与 ,通过面积的计算方法,即可得到两个我们熟悉的公式: .?
18. 已知x2-5x-14=0,求(x-1)(2x-1)-(x+1)2+1的值.
19. 在公式(a+b)2=a2+2ab+b2中,如果我们把a+b,a2+b2,ab分别看做一个整体,那么只要知道其中两项的值,就可以求出第三项的值.
已知a+b=6,ab=-27,求下列各式的值:
(1)a2+b2;(2)a2+b2-ab;(3)(a-b)2.
20. 有一系列等式:
1×2×3×4+1=52=(12+3×1+1)2
2×3×4×5+1=112=(22+3×2+1)2
3×4×5×6+1=192=(32+3×3+1)2
4×5×6×7+1=292=(42+3×4+1)2
…
(1)根据你的观察、归纳、发现的规律,写出8×9×10×11+1的结果 ;
(2)试猜想n(n+1)(n+2)(n+3)+1是哪一个数的平方,并予以证明.
参 考 答 案
1. D
2. C
3. 解:(1)原式=(4a)2+2·4a·b+b2=16a2+8ab+b2.
(2)原式=[-(2m+1)]2=(2m+1)2=4m2+4m+1.
4. B
5. 解:因为(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2,所以(a+b)2-(a-b)2=4ab,所以(a+b)2-4ab=(a-b)2. 因为a+b=2,ab=1,所以(a-b)2=22-4×1=0.
6. 解:(1)1032=(100+3)2=1002+2×100×3+32=10 000+600+9=10 609.
(2)1982=(200-2)2=2002-2×200×2+22=40 000-800+4=39 204.
7. 解:原式=x2+4x+4+2x-x2=6x+4,当x=时,原式=6×+4=6.
8. B
9. C
10. D
11. D
12. C
13. 3
14. 7
15. ±10
16. 7
17. (a+b)2 (a-b)2 (a+b)2=a2+2ab+b2与(a-b)2=a2-2ab+b2
18. 解:原式=2x2-3x+1-x2-2x-1+1=x2-5x+1. 由x2-5x-14=0得x2-5x=14. 故原式=14+1=15.
19. 解:(1)由a+b=6,得(a+b)2=36,即a2+b2+2ab=36. 因为ab=-27,所以a2+b2=36-2×(-27)=90.
(2)由(1)得a2+b2=90,因为ab=-27,所以a2+b2-ab=90-(-27)=117.
(3)(a-b)2=a2-2ab+b2=a2+b2-2ab=90-2×(-27)=144.
20. 解:(1)892 提示:根据观察、归纳、发现的规律,得到8×9×10×11+1=(82+3×8+1)2=892.
(2)依此类推n(n+1)(n+2)(n+3)+1=(n2+3n+1)2,理由如下:等式左边=(n2+3n)(n2+3n+2)+1=n4+6n3+9n2+2n2+6n+1=n4+6n3+11n2+6n+1,等式右边=(n2+3n+1)2=(n2+1)2+2·3n·(n2+1)+9n2=n4+2n2+1+6n3+6n+9n2=n4+6n3+11n2+6n+1,左边=右边.
第8章 整式乘法与因式分解
8.3 完全平方公式与平方差公式
第1课时 完全平方公式
要点测评 基础达标
要点1 完全平方公式
1. 若4a2+kab+9b2是完全平方式,则常数k的值为( )
A. 6 B. 12 C. ±6 D. ±12
2. 下列各式中,与(-a+1)2相等的是( )
A. a2-1 B. a2+1 C. a2-2a+1 D. a2+2a+1
3. 计算:
(1)(4a+b)2; (2)(-2m-1)2.
要点2 完全平方公式的应用
4. 若a+b=3,a2+b2=7,则ab等于( )
A. 2 B. 1 C. -2 D. -1
5. 已知a+b=2,ab=1,求(a-b)2的值.
6. 运用公式简便计算:
(1)1032; (2)1982.
7. 先化简,再求值:(x+2)2+x(2-x),其中x=.
课后集训 巩固提升
8. 下列多项式不是完全平方式的是( )
A. 9a2+6a+1 B. x2-4x-4
C. 4t2-12t+9 D. t2+t+1
9. 一个正方形的边长为a cm,若边长增加6 cm,则新正方形的面积增加了( )
A. 36 cm2 B. 12a cm2 C. (36+12a)cm2 D. 以上都不对
10. 如果ax2+2x+=(2x+)2+m,则a,m的值分别是( )
A. 2,0 B. 4,0 C. 2, D. 4,
11. 已知(x+y)2=12,(x-y)2=4,则x2+3xy+y2的值为( )
A. 8 B. 10 C. 12 D. 14
12. 如图,通过计算大正方形的面积,可以验证一个等式,这个等式是( )
A. (x+y+z)2=x2+y2+z2+2y+xz+yz B. (x+y+z)2=x2+y2+z+2xy+xz+2yz
C. (x+y+z)2=x2+y2+z2+2xy+2xz+2yz D. (x+y+z)2=(x+y)2+2xz+2yz
13. 如果(a+b)2=5,(a-b)2=1,则a2+b2= .?
14. 若a2-3a+1=0,则a2+= .?
15. 若代数式x2+kx+25是一个完全平方式,则k= .
16. 如果3x-2的值为,那么9x2-12x+5的值是 .?
17. 两个图阴影部分面积分别为 与 ,通过面积的计算方法,即可得到两个我们熟悉的公式: .?
18. 已知x2-5x-14=0,求(x-1)(2x-1)-(x+1)2+1的值.
19. 在公式(a+b)2=a2+2ab+b2中,如果我们把a+b,a2+b2,ab分别看做一个整体,那么只要知道其中两项的值,就可以求出第三项的值.
已知a+b=6,ab=-27,求下列各式的值:
(1)a2+b2;(2)a2+b2-ab;(3)(a-b)2.
20. 有一系列等式:
1×2×3×4+1=52=(12+3×1+1)2
2×3×4×5+1=112=(22+3×2+1)2
3×4×5×6+1=192=(32+3×3+1)2
4×5×6×7+1=292=(42+3×4+1)2
…
(1)根据你的观察、归纳、发现的规律,写出8×9×10×11+1的结果 ;
(2)试猜想n(n+1)(n+2)(n+3)+1是哪一个数的平方,并予以证明.
参 考 答 案
1. D
2. C
3. 解:(1)原式=(4a)2+2·4a·b+b2=16a2+8ab+b2.
(2)原式=[-(2m+1)]2=(2m+1)2=4m2+4m+1.
4. B
5. 解:因为(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2,所以(a+b)2-(a-b)2=4ab,所以(a+b)2-4ab=(a-b)2. 因为a+b=2,ab=1,所以(a-b)2=22-4×1=0.
6. 解:(1)1032=(100+3)2=1002+2×100×3+32=10 000+600+9=10 609.
(2)1982=(200-2)2=2002-2×200×2+22=40 000-800+4=39 204.
7. 解:原式=x2+4x+4+2x-x2=6x+4,当x=时,原式=6×+4=6.
8. B
9. C
10. D
11. D
12. C
13. 3
14. 7
15. ±10
16. 7
17. (a+b)2 (a-b)2 (a+b)2=a2+2ab+b2与(a-b)2=a2-2ab+b2
18. 解:原式=2x2-3x+1-x2-2x-1+1=x2-5x+1. 由x2-5x-14=0得x2-5x=14. 故原式=14+1=15.
19. 解:(1)由a+b=6,得(a+b)2=36,即a2+b2+2ab=36. 因为ab=-27,所以a2+b2=36-2×(-27)=90.
(2)由(1)得a2+b2=90,因为ab=-27,所以a2+b2-ab=90-(-27)=117.
(3)(a-b)2=a2-2ab+b2=a2+b2-2ab=90-2×(-27)=144.
20. 解:(1)892 提示:根据观察、归纳、发现的规律,得到8×9×10×11+1=(82+3×8+1)2=892.
(2)依此类推n(n+1)(n+2)(n+3)+1=(n2+3n+1)2,理由如下:等式左边=(n2+3n)(n2+3n+2)+1=n4+6n3+9n2+2n2+6n+1=n4+6n3+11n2+6n+1,等式右边=(n2+3n+1)2=(n2+1)2+2·3n·(n2+1)+9n2=n4+2n2+1+6n3+6n+9n2=n4+6n3+11n2+6n+1,左边=右边.
