北师大版八年级下册数学1.3《线段的垂直平分线 》同步习题(解析版)
文档属性
| 名称 | 北师大版八年级下册数学1.3《线段的垂直平分线 》同步习题(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 338.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览



文档简介
北师大版八年级下册1.3《线段的垂直平分线 》同步习题
一.选择题(共9小题)
1.如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线DE分别交AB、BC于点D、E,则∠BAE=( )
A.80° B.60° C.50° D.40°
2.如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
A.4cm B.3cm C.2cm D.1cm
3.如图,在△ABC中,∠C=90°,AB的垂直平分线交AB于D,交BC于E,连接AE,若CE=5,AC=12,则BE的长是( )
A.5 B.10 C.12 D.13
4.如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )
A.10cm B.12cm C.15cm D.17cm
5.如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为( )
A.1cm B.2cm C.3cm D.4cm
6.如图,在△ABC中,DE是边AC的垂直平分线,AE=5cm,△ABD的周长为26cm,则△ABC的周长为( )
A.32 B.29 C.38 D.36
7.如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为( )
A.48° B.36° C.30° D.24°
8.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E.△ABC的周长为19,△ACE的周长为13,则AB的长为( )
A.3 B.6 C.12 D.16
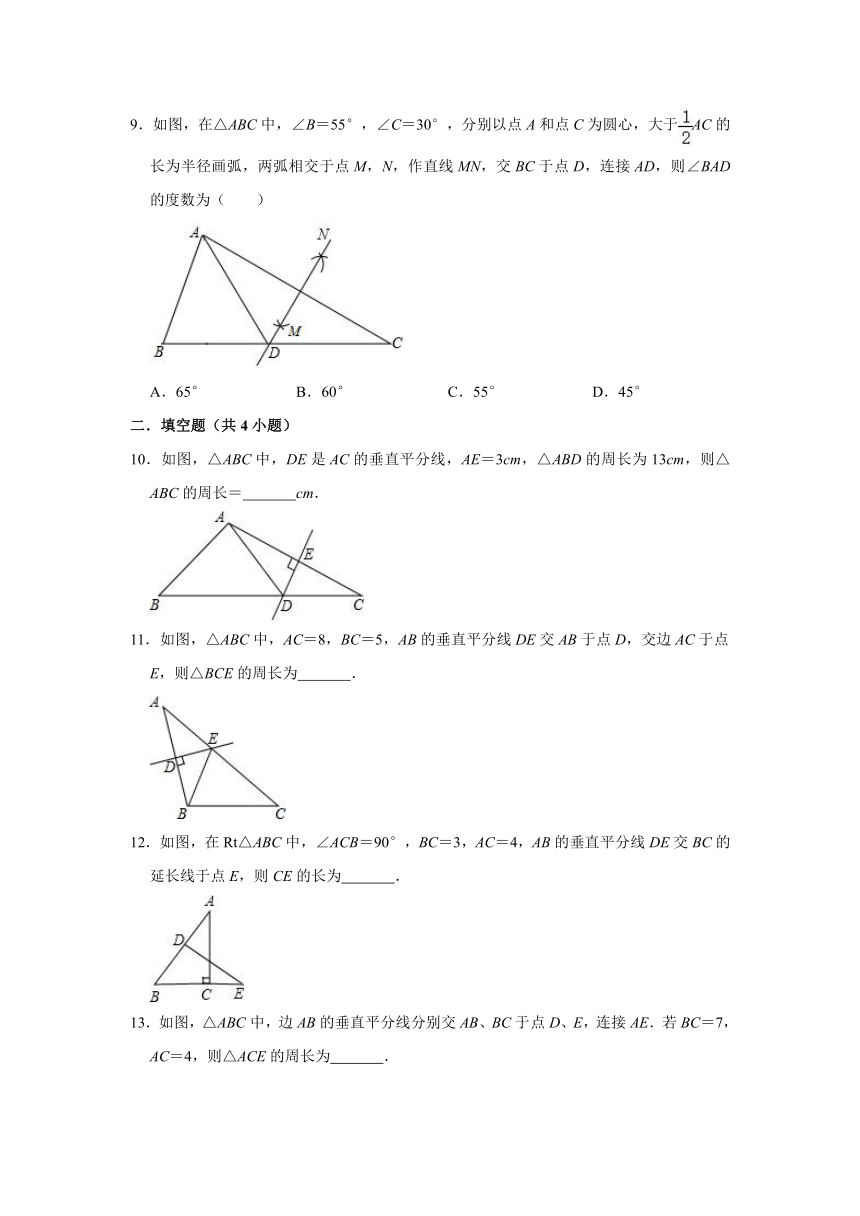
9.如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
A.65° B.60° C.55° D.45°
二.填空题(共4小题)
10.如图,△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长= cm.
11.如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为 .
12.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为 .
13.如图,△ABC中,边AB的垂直平分线分别交AB、BC于点D、E,连接AE.若BC=7,AC=4,则△ACE的周长为 .
三.解答题(共7小题)
14.已知:如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BE=CF,求证:AD是BC的中垂线.
15.如图,在△ABC中,AB的垂直平分线MN交AB于点E,交AC于点D,且AC=15cm,△BCD的周长等于25cm.
(1)求BC的长;
(2)若∠A=36°,并且AB=AC,求证:BC=BD.
16.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
17.如图,Rt△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过点D作AB的垂线交AC于点E,求证:BE垂直平分CD.
18.如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
19.如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
20.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=5,求△ADE的周长.
(2)若∠BAC=120°,求∠DAE的度数.
参考答案与试题解析
一.选择题(共9小题)
1.如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线DE分别交AB、BC于点D、E,则∠BAE=( )
A.80° B.60° C.50° D.40°
【分析】首先利用三角形的内角和定理和等腰三角形的性质∠B,利用线段垂直平分线的性质易得AE=BE,∠BAE=∠B.
【解答】解:∵AB=AC,∠BAC=100°,
∴∠B=∠C=(180°﹣100°)÷2=40°,
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠BAE=∠B=40°,
故选:D.
2.如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
A.4cm B.3cm C.2cm D.1cm
【分析】连接AM、AN、过A作AD⊥BC于D,求出AB、AC值,求出BE、CF值,求出BM、CN值,代入MN=BC﹣BM﹣CN求出即可.
【解答】解:
连接AM、AN、过A作AD⊥BC于D,
∵在△ABC中,AB=AC,∠A=120°,BC=6cm,
∴∠B=∠C=30°,BD=CD=3cm,
∴AB==2cm=AC,
∵AB的垂直平分线EM,
∴BE=AB=cm
同理CF=cm,
∴BM==2cm,
同理CN=2cm,
∴MN=BC﹣BM﹣CN=2cm,
故选:C.
3.如图,在△ABC中,∠C=90°,AB的垂直平分线交AB于D,交BC于E,连接AE,若CE=5,AC=12,则BE的长是( )
A.5 B.10 C.12 D.13
【分析】根据勾股定理,可得AE的长,再根据线段垂直平分线的性质,可得答案.
【解答】解:在Rt△ACE中,由勾股定理,得
AE==13.
由线段的垂直平分线的性质,得
BE=AE=13,
故选:D.
4.如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )
A.10cm B.12cm C.15cm D.17cm
【分析】由△ABC中,边AB的中垂线分别交BC、AB于点D、E,AE=3cm,根据线段垂直平分线的性质,即可求得AD=BD,AB=2AE,又由△ADC的周长为9cm,即可求得AC+BC的值,继而求得△ABC的周长.
【解答】解:∵△ABC中,边AB的中垂线分别交BC、AB于点D、E,AE=3cm,
∴BD=AD,AB=2AE=6cm,
∵△ADC的周长为9cm,
∴AC+AD+CD=AC+BD+CD=AC+BC=9cm,
∴△ABC的周长为:AB+AC+BC=15cm.
故选:C.
5.如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为( )
A.1cm B.2cm C.3cm D.4cm
【分析】首先根据MN是线段AB的垂直平分线,可得AN=BN,然后根据△BCN的周长是7cm,以及AN+NC=AC,求出BC的长为多少即可.
【解答】解:∵MN是线段AB的垂直平分线,
∴AN=BN,
∵△BCN的周长是7cm,
∴BN+NC+BC=7(cm),
∴AN+NC+BC=7(cm),
∵AN+NC=AC,
∴AC+BC=7(cm),
又∵AC=4cm,
∴BC=7﹣4=3(cm).
故选:C.
6.如图,在△ABC中,DE是边AC的垂直平分线,AE=5cm,△ABD的周长为26cm,则△ABC的周长为( )
A.32 B.29 C.38 D.36
【分析】根据线段的垂直平分线的性质得到DA=DC,AC=2AE=10,根据三角形的周长公式计算,得到答案.
【解答】解:∵DE是边AC的垂直平分线,
∴DA=DC,AC=2AE=10,
∵△ABD的周长为26,
∴AB+BD+AD=AB+BD+CD=AB+BC=26,
∴△ABC的周长=AB+BC+AC=26+10=36(cm),
故选:D.
7.如图,△ABC中,BD平分∠ABC,BC的中垂线交BC于点E,交BD于点F,连接CF.若∠A=60°,∠ABD=24°,则∠ACF的度数为( )
A.48° B.36° C.30° D.24°
【分析】根据角平分线的性质可得∠DBC=∠ABD=24°,然后再计算出∠ACB的度数,再根据线段垂直平分线的性质可得BF=CF,进而可得∠FCB=24°,然后可算出∠ACF的度数.
【解答】解:∵BD平分∠ABC,
∴∠DBC=∠ABD=24°,
∵∠A=60°,
∴∠ACB=180°﹣60°﹣24°×2=72°,
∵BC的中垂线交BC于点E,
∴BF=CF,
∴∠FCB=24°,
∴∠ACF=72°﹣24°=48°,
故选:A.
8.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E.△ABC的周长为19,△ACE的周长为13,则AB的长为( )
A.3 B.6 C.12 D.16
【分析】根据线段垂直平分线的性质和等腰三角形的性质即可得到结论.
【解答】解:∵AB的垂直平分线交AB于点D,
∴AE=BE,
∵△ACE的周长=AC+AE+CE=AC+BC=13,△ABC的周长=AC+BC+AB=19,
∴AB=△ABC的周长﹣△ACE的周长=19﹣13=6,
故选:B.
9.如图,在△ABC中,∠B=55°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为( )
A.65° B.60° C.55° D.45°
【分析】根据线段垂直平分线的性质得到AD=DC,根据等腰三角形的性质得到∠C=∠DAC,求得∠DAC=30°,根据三角形的内角和得到∠BAC=95°,即可得到结论.
【解答】解:由题意可得:MN是AC的垂直平分线,
则AD=DC,故∠C=∠DAC,
∵∠C=30°,
∴∠DAC=30°,
∵∠B=55°,
∴∠BAC=95°,
∴∠BAD=∠BAC﹣∠CAD=65°,
故选:A.
二.填空题(共4小题)
10.如图,△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长= 19 cm.
【分析】由已知条件,利用线段的垂直平分线的性质,得到AD=CD,AC=2AE,结合周长,进行线段的等量代换可得答案.
【解答】解:∵DE是AC的垂直平分线,
∴AD=CD,AC=2AE=6cm,
又∵△ABD的周长=AB+BD+AD=13cm,
∴AB+BD+CD=13cm,
即AB+BC=13cm,
∴△ABC的周长=AB+BC+AC=13+6=19(cm).
故答案为:19.
11.如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为 13 .
【分析】根据线段的垂直平分线的性质得到EA=EB,根据三角形的周长公式计算即可.
【解答】解:∵DE是AB的垂直平分线,
∴EA=EB,
则△BCE的周长=BC+EC+EB=BC+EC+EA=BC+AC=13,
故答案为:13.
12.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为 .
【分析】设CE=x,连接AE,由线段垂直平分线的性质可知AE=BE=BC+CE,在Rt△ACE中,利用勾股定理即可求出CE的长度.
【解答】解:设CE=x,连接AE,
∵DE是线段AB的垂直平分线,
∴AE=BE=BC+CE=3+x,
∴在Rt△ACE中,AE2=AC2+CE2,即(3+x)2=42+x2,
解得x=.
故答案为:.
13.如图,△ABC中,边AB的垂直平分线分别交AB、BC于点D、E,连接AE.若BC=7,AC=4,则△ACE的周长为 11 .
【分析】根据线段垂直平分线的性质得到EB=EA,根据三角形的周长公式计算即可.
【解答】解:∵DE是AB的垂直平分线,
∴EB=EA,
∴△ACE的周长=AE+EC+AC=BE+EC+AC=BC+AC=11,
故答案为:11.
三.解答题(共7小题)
14.已知:如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,BE=CF,求证:AD是BC的中垂线.
【分析】由AD是△ABC的角平分线,DE⊥AB,DF⊥AC,根据角平分线的性质,可得DE=DF,∠BED=∠CFD=90°,继而证得Rt△BED≌Rt△CFD,则可得∠B=∠C,证得AB=AC,然后由三线合一,证得AD是BC的中垂线.
【解答】证明:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
在Rt△BED和Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(SAS),
∴∠B=∠C,
∴AB=AC,
∵AD是△ABC的角平分线,
∴AD是BC的中垂线.
15.如图,在△ABC中,AB的垂直平分线MN交AB于点E,交AC于点D,且AC=15cm,△BCD的周长等于25cm.
(1)求BC的长;
(2)若∠A=36°,并且AB=AC,求证:BC=BD.
【分析】(1)由AB的垂直平分线MN交AB于点E,交AC于点D,可得AD=BD,又由△BCD的周长等于25cm,可得AC+BC=25cm,继而求得答案;
(2)由∠A=36°,并且AB=AC,易求得∠BDC=∠C=72°,即可证得BC=BD.
【解答】(1)解:∵MN是AB的垂直平分线,
∴AD=BD,
∵AC=15cm,△BCD的周长等于25cm,
∴BC+CD+BD=BC+CD+AD=BC+AC=25cm,
∴BC=10cm.
(2)证明:∵∠A=36°,AB=AC,
∴∠ABC=∠C==72°,
∵BD=AD,
∴∠ABD=∠A=36°,
∴∠DBC=∠ABC﹣∠ABD=36°,
∴∠BDC=180°﹣∠DBC﹣∠C=72°,
∴∠C=∠BDC,
∴BC=BD.
16.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
【分析】(1)根据线段的垂直平分线到线段两端点的距离相等即可得证;
(2)首先利用三角形内角和求得∠ABC的度数,然后减去∠ABD的度数即可得到答案;
(3)将△ABC的周长转化为AB+AC+BC的长即可求得.
【解答】解:(1)证明:∵AB的垂直平分线MN交AC于点D,
∴DB=DA,
∴△ABD是等腰三角形;
(2)∵△ABD是等腰三角形,∠A=40°,
∴∠ABD=∠A=40°,∠ABC=∠C=(180°﹣40°)÷2=70°
∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°;
(3)∵AB的垂直平分线MN交AC于点D,AE=6,
∴AB=2AE=12,
∵△CBD的周长为20,
∴AC+BC=20,
∴△ABC的周长=AB+AC+BC=12+20=32.
17.如图,Rt△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过点D作AB的垂线交AC于点E,求证:BE垂直平分CD.
【分析】证明Rt△BDE≌Rt△BCE,根据全等三角形的性质得到ED=EC,根据线段垂直平分线的判定定理证明.
【解答】证明:∵∠ACB=90°,DE⊥AB,
∴∠ACB=∠BDE=90°,
在Rt△BDE和Rt△BCE中,
,
∴Rt△BDE≌Rt△BCE,
∴ED=EC,
∵ED=EC,BD=BC,
∴BE垂直平分CD.
18.如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
【分析】(1)先根据E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA得出△ODE≌△OCE,可得出OD=OC,DE=CE,OE=OE,可得出△DOC是等腰三角形,由等腰三角形的性质即可得出OE是CD的垂直平分线;
(2)先根据E是∠AOB的平分线,∠AOB=60°可得出∠AOE=∠BOE=30°,由直角三角形的性质可得出OE=2DE,同理可得出DE=2EF即可得出结论.
【解答】解:(1)∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴DE=CE,OE=OE,
∴Rt△ODE≌Rt△OCE,
∴OD=OC,
∴△DOC是等腰三角形,
∵OE是∠AOB的平分线,
∴OE是CD的垂直平分线;
(2)∵OE是∠AOB的平分线,∠AOB=60°,
∴∠AOE=∠BOE=30°,
∵EC⊥OB,ED⊥OA,
∴OE=2DE,∠ODF=∠OED=60°,
∴∠EDF=30°,
∴DE=2EF,
∴OE=4EF.
19.如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
【分析】(1)根据线段垂直平分线得出AF=DF,根据等腰三角形的性质推出∠FAD=∠FDA,
(2)根据角平分线得出∠BAD=∠CAD,根据三角形外角性质推出即可.
【解答】解:(1)∵AD的垂直平分线交BC的延长线于点F,
∴AF=DF,
∴∠FAD=∠FDA;
(2)∵∠FAD=∠FAC+∠CAD,∠FDA=∠B+∠BAD,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠FAC=∠B=50°.
故答案为:50°.
20.如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=5,求△ADE的周长.
(2)若∠BAC=120°,求∠DAE的度数.
【分析】(1)根据线段垂直平分线的性质得到DA=DB,EA=EC,根据三角形的周长公式计算;
(2)根据三角形内角和定理求出∠B+∠C=60°,根据等边对等角、结合图形计算即可.
【解答】解:(1)∵边AB、AC的垂直平分线分别交BC于D、E,
∴DA=DB,EA=EC,
∴△ADE的周长=AD+DE+AE=DB+DE+EC=BC=5;
(2)∵∠BAC=120°,
∴∠B+∠C=60°,
∵DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
∴∠DAE=∠BAC﹣(∠DAB+∠EAC)=∠BAC﹣(∠B+∠C)=60°.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
