8.3.2 平方差公式(要点测评+课后集训+答案)
文档属性
| 名称 | 8.3.2 平方差公式(要点测评+课后集训+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览


文档简介
沪科版数学七年级下册同步课时训练
第8章 整式乘法与因式分解
8.3 完全平方公式与平方差公式
第2课时 平方差公式
要点测评 基础达标
要点1 平方差公式
1. 下列各式中不能用平方差公式计算的是( )
A. (x-y)(-x+y) B. (-x+y)(-x-y)
C. (-x-y)(x-y) D. (x+y)(-x+y)
2. 计算:
(1)(5x2+3y2)(5x2-3y2); (2)(-2x2-5)(2x2-5);
(3)(1-a)(a+1)(a2+1)(a4+1).
3. 运用平方差公式计算:
(1)1 007×993; (2)12×11;
(3)-19×20.
要点2 平方差公式的应用
4. 计算:852-152= .
5. 已知a+b=3,a-b=5,则代数式a2-b2的值是 . ?
6. 广场内有一块边长为2a米的正方形草坪,经统一规划后,南北方向要缩短3米,东西方向要加长3米,则改造后的长方形草坪的面积是多少?
要点3 乘法公式的应用
7. (3x+4y-6)2展开式的常数项是( )
A. -12 B. -6 C. 9 D. 36
8. 运用乘法公式计算:
(1)(a-b+c)(a+b-c); (2)(2x-y+1)(-y-1+2x);
(3)(a+3)3.
课后集训 巩固提升
9. (x+2)(x-2)(x2+4)的计算结果是( )
A. x4+16 B. -x4-16 C. x4-16 D. 16-x4
10. 如果用平方差公式计算(x-y+5)(x+y+5),则可将原式变形为( )
A. [(x-y)+5][(x+y)+5] B. [(x-y)+5][(x-y)-5]
C. [(x+5)-y][(x+5)+y] D. [x-(y+5)][x+(y+5)]
11. 若x2-y2=30,且x-y=-5,则x+y的值是( )
A. 5 B. 6 C. -6 D. -5
12. 对于任意的正整数n,能整除代数式(3n+1)(3n-1)-(3-n)(3+n)的整数是( )
A. 3 B. 6 C. 10 D. 9
13. 下列计算中,错误的有( )
①(3a+4)(3a-4)=9a2-4;②(2a2-b)(2a2+b)=4a2-b2; ③(3-x)(x+3)=x2-9;④(-x+y)·(x+y)=-(x-y)(x+y)=-x2-y2.
A. 1个 B. 2个 C. 3个 D. 4个
14. 算式(2+1)×(22+1)×(24+1)×…×(232+1)+1计算结果的个位数字是( )
A. 4 B. 2 C. 8 D. 6
15. (a+b-1)(a-b+1)=( )2-( )2.?
16. (1)(a+2b-c)2= ;?
(2)(a+b-2c)2= .?
17. 两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是 .?
18. 计算:
(1)(2x+3)(2x-3); (2)(b+2a)(2a-b);
(3)(-x+2y)(-x-2y); (4)(a+2)(a-2)+a(1-a).
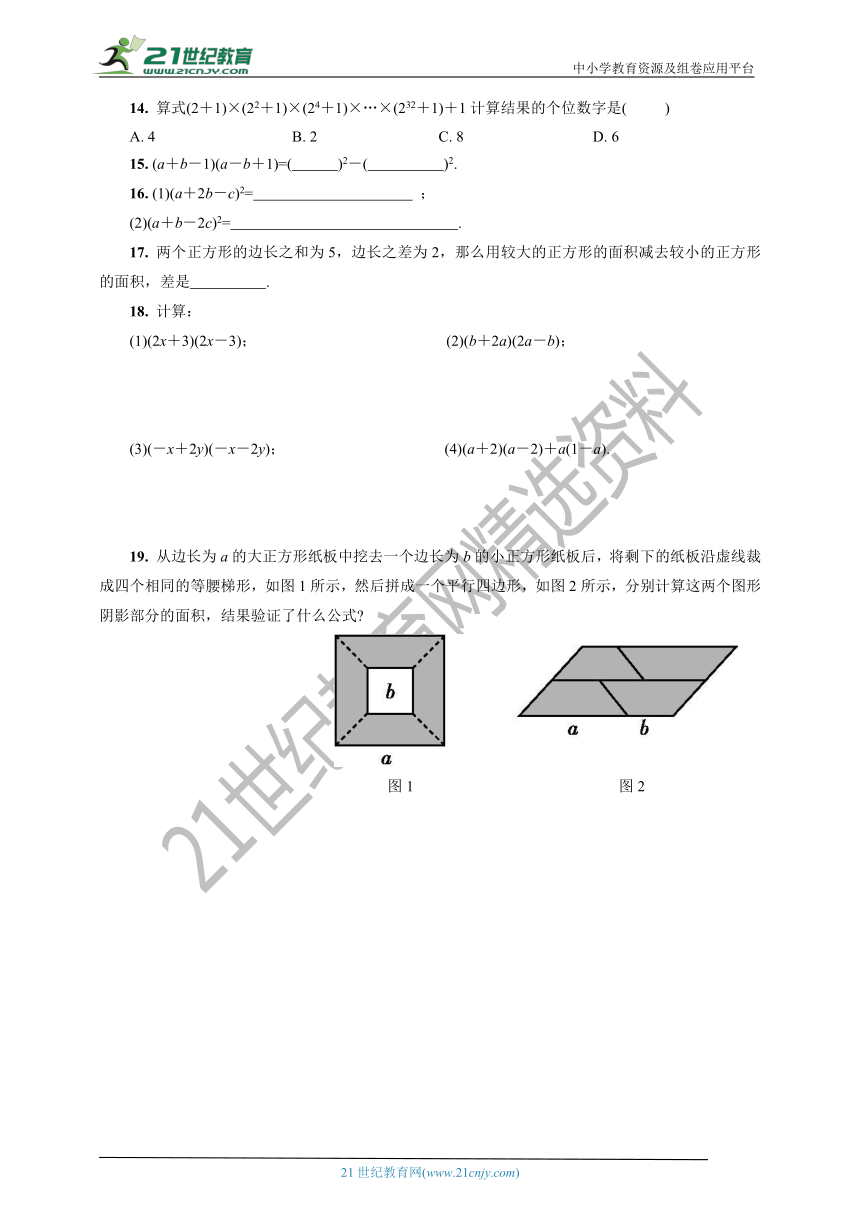
19. 从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将剩下的纸板沿虚线裁成四个相同的等腰梯形,如图1所示,然后拼成一个平行四边形,如图2所示,分别计算这两个图形阴影部分的面积,结果验证了什么公式?
图1 图2
参 考 答 案
1. A
2. 解:(1)原式=(5x2)2-(3y2)2=25x4-9y4.
(2)原式=(-5-2x2)(-5+2x2)=(-5)2-(2x2)2=25-4x4.
(3)原式=(1-a2)(1+a2)(1+a4)=(1-a4)(1+a4)=1-a8.
3. 解:(1)1 007×993=(1 000+7)(1 000-7)=1 0002-72=999 951.
(2)12×11=(12+)(12-)=122-()2=144-=.
(3)-19×20=-(20-)(20+)=-[202-()2]=-399.96.
4. 7 000
5. 15
6. 解:(2a+3)(2a-3)=(2a)2-32=(4a2-9)(平方米). 答:改造后的长方形草坪的面积是(4a2-9)平方米.
7. D
8. 解:(1)(a-b+c)(a+b-c)=[a-(b-c)][a+(b-c)]=a2-(b-c)2=a2-(b2-2bc+c2)=a2-b2+2bc-c2.
(2)(2x-y+1)(-y-1+2x)=(2x-y+1)(2x-y-1)=[(2x-y)+1][(2x-y)-1]=(2x-y)2-1=4x2-4xy+y2-1.
(3)(a+3)3=(a+3)(a+3)2=(a+3)(a2+6a+9)=a3+6a2+9a+3a2+18a+27=a3+9a2+27a+27.
9. C
10. C
11. C
12. C
13. D
14. D
15. a b-1
16. (1)a2+4ab+4b2-2ac-4bc+c2 (2)a2+2ab+b2-4ac-4bc+4c2
17. 10
18. 解:(1)原式=(2x)2-32=4x2-9.
(2)原式=(2a+b)(2a-b)=(2a)2-b2=4a2-b2.
(3)原式=(-x)2-(2y)2=x2-4y2.
(4)原式=a2-4+a-a2=a-4.
19. 解:题图1中的阴影部分(四个等腰梯形)的面积为a2-b2,题图2中的阴影部分(平行四边形)的底为(a+b),这个底上的高为(a-b),故它的面积为(a+b)(a-b),由此可验证:(a+b)(a-b)=a2-b2.
第8章 整式乘法与因式分解
8.3 完全平方公式与平方差公式
第2课时 平方差公式
要点测评 基础达标
要点1 平方差公式
1. 下列各式中不能用平方差公式计算的是( )
A. (x-y)(-x+y) B. (-x+y)(-x-y)
C. (-x-y)(x-y) D. (x+y)(-x+y)
2. 计算:
(1)(5x2+3y2)(5x2-3y2); (2)(-2x2-5)(2x2-5);
(3)(1-a)(a+1)(a2+1)(a4+1).
3. 运用平方差公式计算:
(1)1 007×993; (2)12×11;
(3)-19×20.
要点2 平方差公式的应用
4. 计算:852-152= .
5. 已知a+b=3,a-b=5,则代数式a2-b2的值是 . ?
6. 广场内有一块边长为2a米的正方形草坪,经统一规划后,南北方向要缩短3米,东西方向要加长3米,则改造后的长方形草坪的面积是多少?
要点3 乘法公式的应用
7. (3x+4y-6)2展开式的常数项是( )
A. -12 B. -6 C. 9 D. 36
8. 运用乘法公式计算:
(1)(a-b+c)(a+b-c); (2)(2x-y+1)(-y-1+2x);
(3)(a+3)3.
课后集训 巩固提升
9. (x+2)(x-2)(x2+4)的计算结果是( )
A. x4+16 B. -x4-16 C. x4-16 D. 16-x4
10. 如果用平方差公式计算(x-y+5)(x+y+5),则可将原式变形为( )
A. [(x-y)+5][(x+y)+5] B. [(x-y)+5][(x-y)-5]
C. [(x+5)-y][(x+5)+y] D. [x-(y+5)][x+(y+5)]
11. 若x2-y2=30,且x-y=-5,则x+y的值是( )
A. 5 B. 6 C. -6 D. -5
12. 对于任意的正整数n,能整除代数式(3n+1)(3n-1)-(3-n)(3+n)的整数是( )
A. 3 B. 6 C. 10 D. 9
13. 下列计算中,错误的有( )
①(3a+4)(3a-4)=9a2-4;②(2a2-b)(2a2+b)=4a2-b2; ③(3-x)(x+3)=x2-9;④(-x+y)·(x+y)=-(x-y)(x+y)=-x2-y2.
A. 1个 B. 2个 C. 3个 D. 4个
14. 算式(2+1)×(22+1)×(24+1)×…×(232+1)+1计算结果的个位数字是( )
A. 4 B. 2 C. 8 D. 6
15. (a+b-1)(a-b+1)=( )2-( )2.?
16. (1)(a+2b-c)2= ;?
(2)(a+b-2c)2= .?
17. 两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是 .?
18. 计算:
(1)(2x+3)(2x-3); (2)(b+2a)(2a-b);
(3)(-x+2y)(-x-2y); (4)(a+2)(a-2)+a(1-a).
19. 从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将剩下的纸板沿虚线裁成四个相同的等腰梯形,如图1所示,然后拼成一个平行四边形,如图2所示,分别计算这两个图形阴影部分的面积,结果验证了什么公式?
图1 图2
参 考 答 案
1. A
2. 解:(1)原式=(5x2)2-(3y2)2=25x4-9y4.
(2)原式=(-5-2x2)(-5+2x2)=(-5)2-(2x2)2=25-4x4.
(3)原式=(1-a2)(1+a2)(1+a4)=(1-a4)(1+a4)=1-a8.
3. 解:(1)1 007×993=(1 000+7)(1 000-7)=1 0002-72=999 951.
(2)12×11=(12+)(12-)=122-()2=144-=.
(3)-19×20=-(20-)(20+)=-[202-()2]=-399.96.
4. 7 000
5. 15
6. 解:(2a+3)(2a-3)=(2a)2-32=(4a2-9)(平方米). 答:改造后的长方形草坪的面积是(4a2-9)平方米.
7. D
8. 解:(1)(a-b+c)(a+b-c)=[a-(b-c)][a+(b-c)]=a2-(b-c)2=a2-(b2-2bc+c2)=a2-b2+2bc-c2.
(2)(2x-y+1)(-y-1+2x)=(2x-y+1)(2x-y-1)=[(2x-y)+1][(2x-y)-1]=(2x-y)2-1=4x2-4xy+y2-1.
(3)(a+3)3=(a+3)(a+3)2=(a+3)(a2+6a+9)=a3+6a2+9a+3a2+18a+27=a3+9a2+27a+27.
9. C
10. C
11. C
12. C
13. D
14. D
15. a b-1
16. (1)a2+4ab+4b2-2ac-4bc+c2 (2)a2+2ab+b2-4ac-4bc+4c2
17. 10
18. 解:(1)原式=(2x)2-32=4x2-9.
(2)原式=(2a+b)(2a-b)=(2a)2-b2=4a2-b2.
(3)原式=(-x)2-(2y)2=x2-4y2.
(4)原式=a2-4+a-a2=a-4.
19. 解:题图1中的阴影部分(四个等腰梯形)的面积为a2-b2,题图2中的阴影部分(平行四边形)的底为(a+b),这个底上的高为(a-b),故它的面积为(a+b)(a-b),由此可验证:(a+b)(a-b)=a2-b2.
