沪科版数学七年级下册 8.2.1 第1课时 单项式乘单项式课件(共18张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 8.2.1 第1课时 单项式乘单项式课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 49.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-04 00:00:00 | ||
图片预览


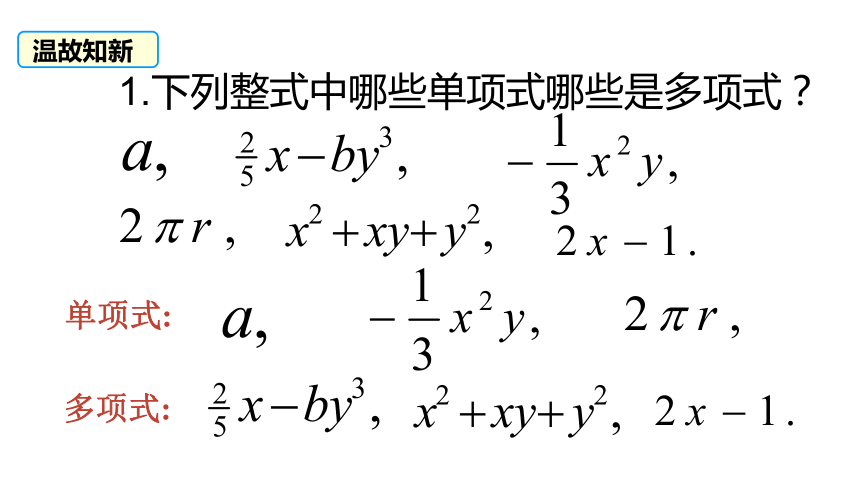




文档简介
(共18张PPT)
8.2 整式乘法
8.2.1 单项式与单项式相乘
第1课时 单项式乘单项式
学习目标:
经历探究单项式与单项式运算法则的过程,发展观察、归纳、猜测、验证等能力,会进行单项式与单项式相乘的运算;
理解单项式乘法算理,体会乘法运算律的作用和转化思想;
培养学生的语言表达能力、逻辑思维能力。
单项式:
多项式:
1.下列整式中哪些单项式哪些是多项式?
温故知新
2、利用乘法的交换律,结合律计算:
6×4×13×25
解:原式= (6 ×13) ×(4×25)
=78 ×100
=7800
3.前面学习了哪些幂的运算?运算法则分别是什么?
4.计算下列各题:
(1)(-a5)3; (2)(-a2b)3 ;
=a15
(3) (-2a)2(-3a2)3 ;
=-4a2(-27a6)=108a8
(4) (-y n)2 ÷y n-1.
am÷an=am-n
(am)n= amn
(ab)n= anbn
=-a6b3
=y2n÷y n-1
=y2n-n+1
=y n+1
情境
北京天安门
天安门广场
天安门广场
有一位外国记者用步长测量天安门广场的面积:他从北走到南,记下所走的步数为1100步;再从东走到西,记下所走的步数为625步,然后根据自己的步长来估算广场的面积
(1)如果用字母a表示该记者的步长,你能用含a的代数式表示广场的面积吗?
考一考
(2)假设这位记者的步长为0.8m,那么广场的面积大约是多少?
(3)通过解决上述问题,你认为两个单项式相乘应怎样运算?运算依据是什么?
探究尝试
(1)2c5?5c2=(2×5)(c5?c2)=10c7
(2)(-5a2b3)?(-4b2c)=[-5×(-4)]a2(b3?b2)c
各单项式的相同字母相乘
各单项式的系数相乘
各单项式的系数相乘
各单项式的相同字母相乘
只在一个单项式里含有的字母连
同它的指数作为积的一个因式
从以上的计算过程中,你能归纳出单项式乘法的法则吗
单项式与单项式相乘
单项式×单项式
=(系数×系数)(同底数幂相乘)(单独的幂)
单项式的乘法法则
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
简记为:
归纳结论
典例
例1 计算:
(1)2xy2? xy; (2) (-2a2b3?(-3a);
(3)7xy2z?(2xyz)2.
解:(1)原式=(2× )?(x?x)?(y2?y)=
(2)原式=[(-2)×(-3)]?(a2a)?b3 =6a3b3.
(3)原式=7xy2z?4x2y2z2
=(7×4)?(xx2)?(y2y2)?(zz2)
=28x3y4z3.
跟踪练习
1.计算:①3x · 5x2
②(-2y)·(3xy5)
③(-2.5x)·(-4x)
④x2yz · xyz3·z2
⑤(2×105)(2×105)
⑥(-2x)3(-4x2)
⑦xm+1y · 6xym-1
15x3
-6xy6
10x2
x3 y2 z6
4×1010
=(-8x3)·(-4x2)
=32x5
6xm+2ym
对于它们的计算过程和结果你有什么发现呢?
注意:
单项式乘单项式的结果仍是单项式,只是系数和指数发生了变化,对于三个和三个以上单项式相乘,此法则仍然使用;
单项式乘法中,若有乘方、乘法混合运算,要按“先乘方,再乘法”的顺序进行。
4a2?2a4=8a8 ( )
6a3?5a2=11a5 ( )
(-7a)?(-3a3)=-21a4 ( )
3a2b?4a3=12a5 ( )
×
×
×
×
同底数幂的乘法,底数不变,指数相加
系数相乘
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏。
求系数的积,应注意符号
2.判断正误
例2 判断下题的解答过程是否正确,若不正确,说明错误原因并改正。
乘方与乘法运算顺序错误
幂的乘方与幂的乘法混淆错误
3.如图,阴影部分的面积是多少?
2y
3x
0.5x
y
解:
答:阴影部分的面积为 。
4.已知单项式 与单项式 的积与
是同类项,求m,n的值。
单项式乘单项式中的“一、二、三”
一个不变
单项式与单项式相乘时,对于只在一个单项式里含有的字母,连同它的指数不变,作为积的因式.
二个相乘
把各个单项式中的系数、相同字母的幂分别相乘.
三个检验
单项式乘单项式的结果是否正确,可从以下三个方面来检验:
①结果仍是单项式;
②结果中含有单项式中的所有字母;
③结果中每一个字母的指数都等于前面单项式中同一字母的指数和.
归纳总结:
课后作业:
第57页的练习。
8.2 整式乘法
8.2.1 单项式与单项式相乘
第1课时 单项式乘单项式
学习目标:
经历探究单项式与单项式运算法则的过程,发展观察、归纳、猜测、验证等能力,会进行单项式与单项式相乘的运算;
理解单项式乘法算理,体会乘法运算律的作用和转化思想;
培养学生的语言表达能力、逻辑思维能力。
单项式:
多项式:
1.下列整式中哪些单项式哪些是多项式?
温故知新
2、利用乘法的交换律,结合律计算:
6×4×13×25
解:原式= (6 ×13) ×(4×25)
=78 ×100
=7800
3.前面学习了哪些幂的运算?运算法则分别是什么?
4.计算下列各题:
(1)(-a5)3; (2)(-a2b)3 ;
=a15
(3) (-2a)2(-3a2)3 ;
=-4a2(-27a6)=108a8
(4) (-y n)2 ÷y n-1.
am÷an=am-n
(am)n= amn
(ab)n= anbn
=-a6b3
=y2n÷y n-1
=y2n-n+1
=y n+1
情境
北京天安门
天安门广场
天安门广场
有一位外国记者用步长测量天安门广场的面积:他从北走到南,记下所走的步数为1100步;再从东走到西,记下所走的步数为625步,然后根据自己的步长来估算广场的面积
(1)如果用字母a表示该记者的步长,你能用含a的代数式表示广场的面积吗?
考一考
(2)假设这位记者的步长为0.8m,那么广场的面积大约是多少?
(3)通过解决上述问题,你认为两个单项式相乘应怎样运算?运算依据是什么?
探究尝试
(1)2c5?5c2=(2×5)(c5?c2)=10c7
(2)(-5a2b3)?(-4b2c)=[-5×(-4)]a2(b3?b2)c
各单项式的相同字母相乘
各单项式的系数相乘
各单项式的系数相乘
各单项式的相同字母相乘
只在一个单项式里含有的字母连
同它的指数作为积的一个因式
从以上的计算过程中,你能归纳出单项式乘法的法则吗
单项式与单项式相乘
单项式×单项式
=(系数×系数)(同底数幂相乘)(单独的幂)
单项式的乘法法则
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
简记为:
归纳结论
典例
例1 计算:
(1)2xy2? xy; (2) (-2a2b3?(-3a);
(3)7xy2z?(2xyz)2.
解:(1)原式=(2× )?(x?x)?(y2?y)=
(2)原式=[(-2)×(-3)]?(a2a)?b3 =6a3b3.
(3)原式=7xy2z?4x2y2z2
=(7×4)?(xx2)?(y2y2)?(zz2)
=28x3y4z3.
跟踪练习
1.计算:①3x · 5x2
②(-2y)·(3xy5)
③(-2.5x)·(-4x)
④x2yz · xyz3·z2
⑤(2×105)(2×105)
⑥(-2x)3(-4x2)
⑦xm+1y · 6xym-1
15x3
-6xy6
10x2
x3 y2 z6
4×1010
=(-8x3)·(-4x2)
=32x5
6xm+2ym
对于它们的计算过程和结果你有什么发现呢?
注意:
单项式乘单项式的结果仍是单项式,只是系数和指数发生了变化,对于三个和三个以上单项式相乘,此法则仍然使用;
单项式乘法中,若有乘方、乘法混合运算,要按“先乘方,再乘法”的顺序进行。
4a2?2a4=8a8 ( )
6a3?5a2=11a5 ( )
(-7a)?(-3a3)=-21a4 ( )
3a2b?4a3=12a5 ( )
×
×
×
×
同底数幂的乘法,底数不变,指数相加
系数相乘
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏。
求系数的积,应注意符号
2.判断正误
例2 判断下题的解答过程是否正确,若不正确,说明错误原因并改正。
乘方与乘法运算顺序错误
幂的乘方与幂的乘法混淆错误
3.如图,阴影部分的面积是多少?
2y
3x
0.5x
y
解:
答:阴影部分的面积为 。
4.已知单项式 与单项式 的积与
是同类项,求m,n的值。
单项式乘单项式中的“一、二、三”
一个不变
单项式与单项式相乘时,对于只在一个单项式里含有的字母,连同它的指数不变,作为积的因式.
二个相乘
把各个单项式中的系数、相同字母的幂分别相乘.
三个检验
单项式乘单项式的结果是否正确,可从以下三个方面来检验:
①结果仍是单项式;
②结果中含有单项式中的所有字母;
③结果中每一个字母的指数都等于前面单项式中同一字母的指数和.
归纳总结:
课后作业:
第57页的练习。
