17.4 一元二次方程的根与系数的关系课件 (共21张PPT)
文档属性
| 名称 | 17.4 一元二次方程的根与系数的关系课件 (共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 20:11:05 | ||
图片预览








文档简介
(共21张PPT)
17.4一元二次方程根与系数的关系
沪科版 八年级下
新知导入
问题:1.一元二次方程根的情况如何确定?
答:①当 >0时,一元二次方程有两个不相等的实数根;
②当 =0时,一元二次方程有两个相等的实数根;
③当 <0时,一元二次方程没有实数根。
2.一元二次方程根与根之间有什么关系呢?
新知讲解
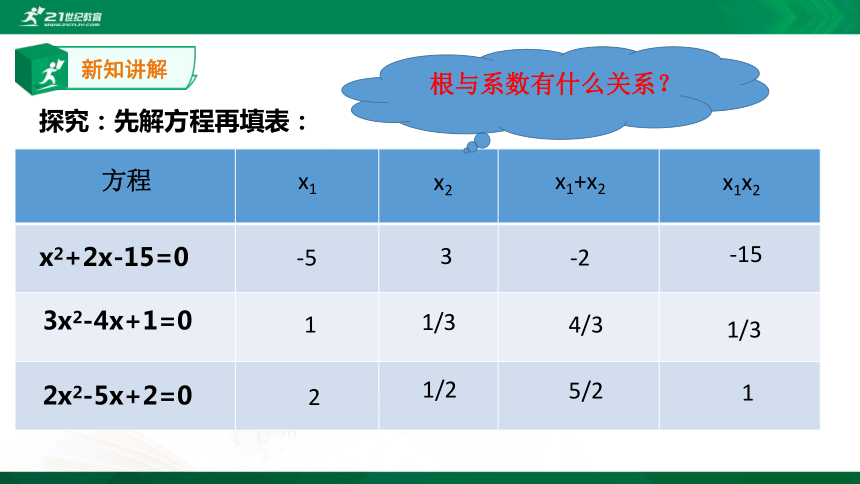
探究:先解方程再填表:
根与系数有什么关系?
方程
x1
x2
x1+x2
x1x2
x2+2x-15=0
-5
3
-2
-15
3x2-4x+1=0
1
1/3
4/3
1/3
2x2-5x+2=0
2
1/2
5/2
1
新知讲解
根据你的观察,猜想:方程ax2+bx+c=0 (a≠0)的根如果是x1,x2,那么x1+x2=——,x1x2=———.
你能证明上面的猜想吗?
我们知道,一元二次方程ax2+bx+c=0 (a≠0)的两根为:
x1= x2 =
所以x1+x2= + =
新知讲解
x1x2= . =
由此得出,一元二次方程根与系数之间存在下列关系:
如果一元二次方程ax2+bx+c=0 (a≠0)的根是x1,x2,
那么x1+x2=——————,x1x2=———————.
这个关系通常称为韦达定理。
当一元二次方程的二次项系数为1时,它的标准形式为x2+px+q=0设两根是x1,x2,这时韦达定理应是:x1+x2=- p, x1x2=q.
新知讲解
例1.已知关于X的一元二次方程2x2+kx-4=0的一个根是-4,求另一个根及k的值.
解:设方程的另一根是x2,则
解得:
答:方程的另一根是1/2,k=7
-4+x2=-k/2
-4x2=-4/2
x2=1/2
k=7
新知讲解
例2.方程x2-3x-4=0的两个根记作x1,x2,不解方程,求下列各式的值。
(1)x12+x22 (2)(x1+1)(x2+1)
(3)1/ x2+1/x1 (4)x12x2+x1x22
(5) x1-x2 (6)x12-x22
解:由韦达定理得:x1+x2= 3 x1x2=-4
(1)x12+x22=(x1+x2)2-2 x1x2=32-2×(-4)=17
新知讲解
(2)(x1+1)(x2+1)=x1x2+x1+x2+1=-4+3+1=0
(3)1/ x2+1/x1 =(x12+x22)/x1x2=-17/4
(4)x12x2+x1x22=x1x2(x1+x2)=-4×3=-12
(5) x1-x2
(x1-x2)2=(x1+x2)2-4x1x2=9+16=25,故x1-x2=±5
(6)x12-x22 =(x1+x2)(x1-x2)=3×(±5)=±15
新知讲解
例3.若长方形的长和宽是方程4x2-12x+3=0的两个根,求该长方形的周长和面积。
解:设长方形的长和宽分别是a,b.
根据韦达定理得:
故长方形的周长为C=2(a+b)=2×3=6
长方形的面积为S=ab=3/4
a+b=3
ab=3/4
新知讲解
例4.已知两数的和为2,积为-2,求这两个数。
解:设这两个数分别为a,b.
由题意得:
所以a,b是一元二次方程x2-2x-2=0的两个根.
解这个方程得:
所以这两个数分别为1+ 和1-
a+b=2
ab=-2
课堂练习
1.一元二次方程x2+x-2=0的两根之积是( )
A. -1 B. -2 C. 1 D.2
2.一元二次方程x2+4x-3=0的两根为x1,x2,则x1x2的值为( )
A. 4 B. -4 C. 3 D.-3
3.已知方程2x2+4x-3=0的两根为x1,x2,则x1+x2的值为————.
B
D
-2
课堂练习
4.已知-1是方程x2+bx+1=4的一个根,求它的另一个根及b的值.
解:设另一个根为a,原方程可化为x2+bx-3=0
根据韦达定理得:
解得:a=3,b=-2
所以原方程的另一个根a=3及b的值为-2.
-1+a=-b
-1×a=-3
课堂练习
5.若x1,x2是一元二次方程x2+2x-2017=0的两根,求下列各式的值:
(1)x12+x22 (2)(x1-5)(x2-5) (3)│x1-x2│
解:根据韦达定理得:x1+x2=-2, x1x2=-2017
(1)x12+x22=(x1+x2)2-2 x1x2=(-2)2-2×(-2017)=4038
(2)(x1-5)(x2-5)=x1x2-5(x1+x2)+25=-2017-5×(-2)+25=-1982
(3)(x1-x2)2=(x1+x2)2-4x1x2=4-4×(-2017)=8072,
故│x1-x2│=8072
拓展提高
6.已知x1,x2是关于X的方程x2-2(m+1)x+m2+5=0的两个实数根.
(1)(x1-1)(x2-1)=28,求m的值.
(2)已知等腰 ABC的一边长为7,若x1,x2恰好是 ABC另外两边的长求这个三角形的周长。
解:根据韦达定理得:x1+x2=2(m+1), x1x2=m2+5
(1)(x1-1)(x2-1)=x1x2-(x1+x2)+1=m2+5-2(m+1)+1=28
原式可化为:m2-2m-24=0
拓展提高
解方程得m1=6,m2=-4
∵原方程有两个实数根,
∴ =4(m+1)2-4(m2+5)=4m2+8m+4-4m2-20
=8m-16≥0
∴m≥2 ∴m=6
(2)当m=6时,原方程可化为x2-14x+41=0
由题意得:x1+x2=14
∴这个三角形的周长为C=7+14=21
中考链接
7.(湘潭.中考)已知关于X方程x2-3x+m=0有两个不相等实数根x1,x2.
(1)求m的取值范围;
(2)当x1=1时,求另一个根x2的值.
解:(1)∵原方程有两个不相等的实数根
∴ =(-3)2-4m=9-4m>0
∴m<9/4.
(2)根据韦达定理得:x1+x2=3,
当x1=1时,另一个根x2的值为2
课堂总结
本节课你有什么收获?
韦达定理:
1.如果一元二次方程ax2+bx+c=0 (a≠0)的根是x1,x2,
那么x1+x2=——————,x1x2=———————.
2.当一元二次方程的二次项系数为1时,它的标准形式为x2+px+q=0设两根是x1,x2,这时韦达定理应是:
x1+x2=- p, x1x2=q.
板书设计
17.4一元二次方程根与系数的关系
1.韦达定理:
2.例1... 例2.... 例3.... 例4...
作业布置
课本 P40 页
习题17.4第1----5题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
17.4一元二次方程根与系数的关系
沪科版 八年级下
新知导入
问题:1.一元二次方程根的情况如何确定?
答:①当 >0时,一元二次方程有两个不相等的实数根;
②当 =0时,一元二次方程有两个相等的实数根;
③当 <0时,一元二次方程没有实数根。
2.一元二次方程根与根之间有什么关系呢?
新知讲解
探究:先解方程再填表:
根与系数有什么关系?
方程
x1
x2
x1+x2
x1x2
x2+2x-15=0
-5
3
-2
-15
3x2-4x+1=0
1
1/3
4/3
1/3
2x2-5x+2=0
2
1/2
5/2
1
新知讲解
根据你的观察,猜想:方程ax2+bx+c=0 (a≠0)的根如果是x1,x2,那么x1+x2=——,x1x2=———.
你能证明上面的猜想吗?
我们知道,一元二次方程ax2+bx+c=0 (a≠0)的两根为:
x1= x2 =
所以x1+x2= + =
新知讲解
x1x2= . =
由此得出,一元二次方程根与系数之间存在下列关系:
如果一元二次方程ax2+bx+c=0 (a≠0)的根是x1,x2,
那么x1+x2=——————,x1x2=———————.
这个关系通常称为韦达定理。
当一元二次方程的二次项系数为1时,它的标准形式为x2+px+q=0设两根是x1,x2,这时韦达定理应是:x1+x2=- p, x1x2=q.
新知讲解
例1.已知关于X的一元二次方程2x2+kx-4=0的一个根是-4,求另一个根及k的值.
解:设方程的另一根是x2,则
解得:
答:方程的另一根是1/2,k=7
-4+x2=-k/2
-4x2=-4/2
x2=1/2
k=7
新知讲解
例2.方程x2-3x-4=0的两个根记作x1,x2,不解方程,求下列各式的值。
(1)x12+x22 (2)(x1+1)(x2+1)
(3)1/ x2+1/x1 (4)x12x2+x1x22
(5) x1-x2 (6)x12-x22
解:由韦达定理得:x1+x2= 3 x1x2=-4
(1)x12+x22=(x1+x2)2-2 x1x2=32-2×(-4)=17
新知讲解
(2)(x1+1)(x2+1)=x1x2+x1+x2+1=-4+3+1=0
(3)1/ x2+1/x1 =(x12+x22)/x1x2=-17/4
(4)x12x2+x1x22=x1x2(x1+x2)=-4×3=-12
(5) x1-x2
(x1-x2)2=(x1+x2)2-4x1x2=9+16=25,故x1-x2=±5
(6)x12-x22 =(x1+x2)(x1-x2)=3×(±5)=±15
新知讲解
例3.若长方形的长和宽是方程4x2-12x+3=0的两个根,求该长方形的周长和面积。
解:设长方形的长和宽分别是a,b.
根据韦达定理得:
故长方形的周长为C=2(a+b)=2×3=6
长方形的面积为S=ab=3/4
a+b=3
ab=3/4
新知讲解
例4.已知两数的和为2,积为-2,求这两个数。
解:设这两个数分别为a,b.
由题意得:
所以a,b是一元二次方程x2-2x-2=0的两个根.
解这个方程得:
所以这两个数分别为1+ 和1-
a+b=2
ab=-2
课堂练习
1.一元二次方程x2+x-2=0的两根之积是( )
A. -1 B. -2 C. 1 D.2
2.一元二次方程x2+4x-3=0的两根为x1,x2,则x1x2的值为( )
A. 4 B. -4 C. 3 D.-3
3.已知方程2x2+4x-3=0的两根为x1,x2,则x1+x2的值为————.
B
D
-2
课堂练习
4.已知-1是方程x2+bx+1=4的一个根,求它的另一个根及b的值.
解:设另一个根为a,原方程可化为x2+bx-3=0
根据韦达定理得:
解得:a=3,b=-2
所以原方程的另一个根a=3及b的值为-2.
-1+a=-b
-1×a=-3
课堂练习
5.若x1,x2是一元二次方程x2+2x-2017=0的两根,求下列各式的值:
(1)x12+x22 (2)(x1-5)(x2-5) (3)│x1-x2│
解:根据韦达定理得:x1+x2=-2, x1x2=-2017
(1)x12+x22=(x1+x2)2-2 x1x2=(-2)2-2×(-2017)=4038
(2)(x1-5)(x2-5)=x1x2-5(x1+x2)+25=-2017-5×(-2)+25=-1982
(3)(x1-x2)2=(x1+x2)2-4x1x2=4-4×(-2017)=8072,
故│x1-x2│=8072
拓展提高
6.已知x1,x2是关于X的方程x2-2(m+1)x+m2+5=0的两个实数根.
(1)(x1-1)(x2-1)=28,求m的值.
(2)已知等腰 ABC的一边长为7,若x1,x2恰好是 ABC另外两边的长求这个三角形的周长。
解:根据韦达定理得:x1+x2=2(m+1), x1x2=m2+5
(1)(x1-1)(x2-1)=x1x2-(x1+x2)+1=m2+5-2(m+1)+1=28
原式可化为:m2-2m-24=0
拓展提高
解方程得m1=6,m2=-4
∵原方程有两个实数根,
∴ =4(m+1)2-4(m2+5)=4m2+8m+4-4m2-20
=8m-16≥0
∴m≥2 ∴m=6
(2)当m=6时,原方程可化为x2-14x+41=0
由题意得:x1+x2=14
∴这个三角形的周长为C=7+14=21
中考链接
7.(湘潭.中考)已知关于X方程x2-3x+m=0有两个不相等实数根x1,x2.
(1)求m的取值范围;
(2)当x1=1时,求另一个根x2的值.
解:(1)∵原方程有两个不相等的实数根
∴ =(-3)2-4m=9-4m>0
∴m<9/4.
(2)根据韦达定理得:x1+x2=3,
当x1=1时,另一个根x2的值为2
课堂总结
本节课你有什么收获?
韦达定理:
1.如果一元二次方程ax2+bx+c=0 (a≠0)的根是x1,x2,
那么x1+x2=——————,x1x2=———————.
2.当一元二次方程的二次项系数为1时,它的标准形式为x2+px+q=0设两根是x1,x2,这时韦达定理应是:
x1+x2=- p, x1x2=q.
板书设计
17.4一元二次方程根与系数的关系
1.韦达定理:
2.例1... 例2.... 例3.... 例4...
作业布置
课本 P40 页
习题17.4第1----5题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
