华师大版八年级数学下册17.5实践与探索作业设计含答案
文档属性
| 名称 | 华师大版八年级数学下册17.5实践与探索作业设计含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 309.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 21:06:17 | ||
图片预览


文档简介
17.5 实践与探索
一、选择题
1.直线过点和点,则方程的解是( ).
A. B. C. D.
2.如图,直线y=﹣x+c与直线y=ax+b的交点坐标为(3,﹣1),关于x的不等式﹣x+c≥ax+b的解集为( )
(第2题图)
A. x≥﹣1 B. x≤﹣1??? ?C. x≥3???? D. x≤3
3.在平面直角坐标系中,方程2x+3y=4所对应的直线为a,方程3x+2y=4所对应的直线为b,直线a与b的交点为P(m,n),下列说法错误的是( )
A. 是方程2x+3y=4的解 B. 是方程3x+2y=4的解
C. 是方程组的解 D. 以上说法均错误
4.若直线y=3x+6与直线y=2x+4的交点坐标为(a,b),则解为的方程组是( )
A. B.
C. D.
5.如图,以两条直线l1,l2的交点坐标为解的方程组是( )
(第5题图)
A. B.
C. D.
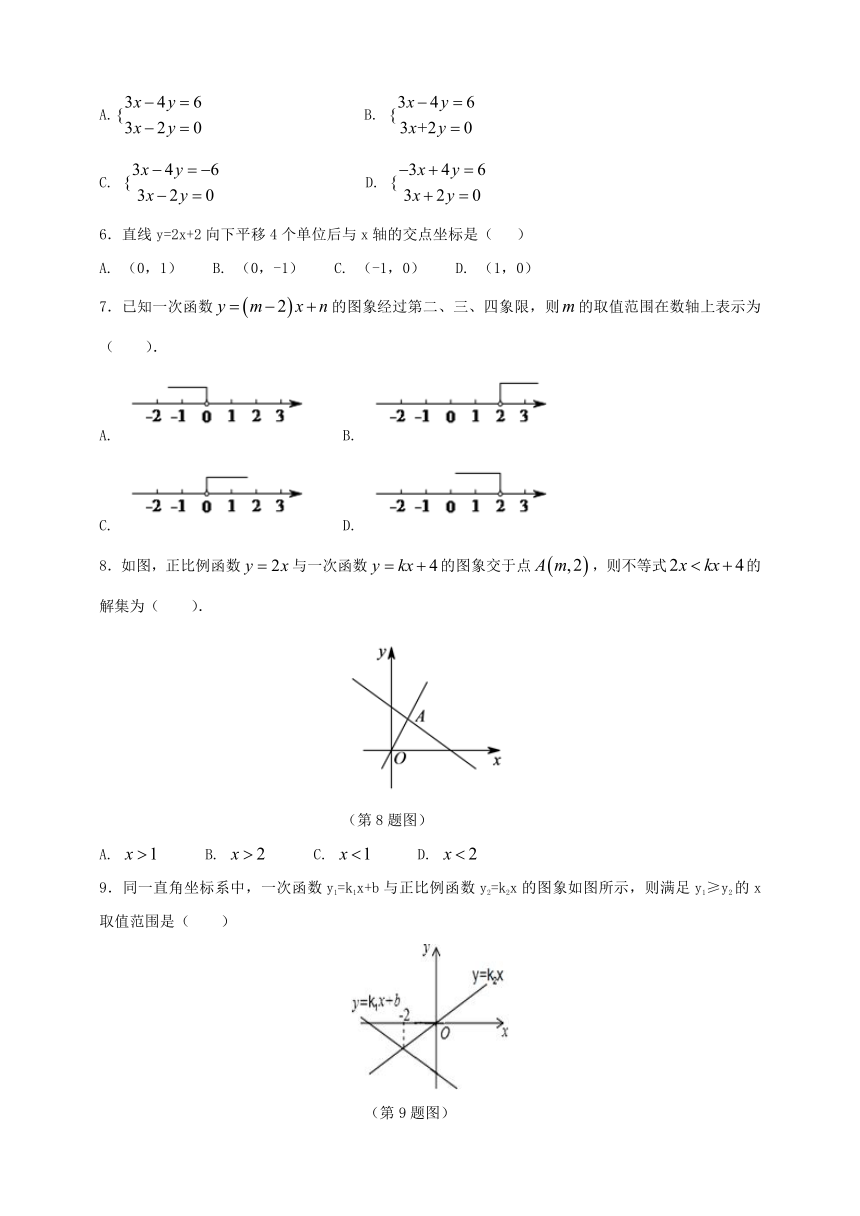
6.直线y=2x+2向下平移4个单位后与x轴的交点坐标是( )
A. (0,1) B. (0,-1) C. (-1,0) D. (1,0)
7.已知一次函数的图象经过第二、三、四象限,则的取值范围在数轴上表示为( ).
A. B.
C. D.
8.如图,正比例函数与一次函数的图象交于点,则不等式的解集为( ).
(第8题图)
A. B. C. D.
9.同一直角坐标系中,一次函数y1=k1x+b与正比例函数y2=k2x的图象如图所示,则满足y1≥y2的x取值范围是( )
(第9题图)
A. x≤﹣2 B. x≥﹣2 C. x<﹣2 D. x>﹣2
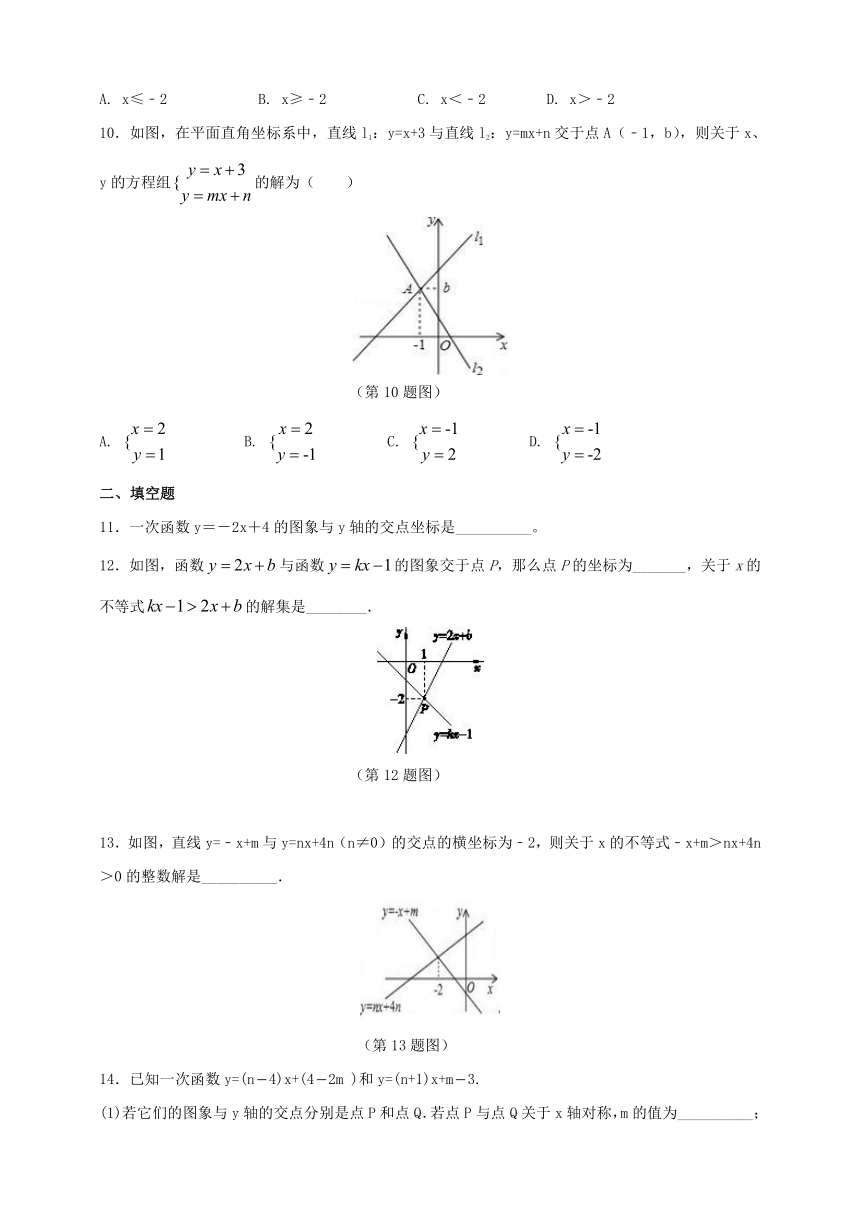
10.如图,在平面直角坐标系中,直线l1:y=x+3与直线l2:y=mx+n交于点A(﹣1,b),则关于x、y的方程组的解为( )
(第10题图)
A. B. C. D.
二、填空题
11.一次函数y=-2x+4的图象与y轴的交点坐标是__________。
12.如图,函数与函数的图象交于点P,那么点P的坐标为_______,关于x的不等式的解集是________.
(第12题图)
13.如图,直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2,则关于x的不等式﹣x+m>nx+4n>0的整数解是__________.
(第13题图)
14.已知一次函数y=(n4)x+(42m )和y=(n+1)x+m3.
(1)若它们的图象与y轴的交点分别是点P和点Q.若点P与点Q关于x轴对称,m的值为__________;
(2)若这两个一次函数的图象交于点(1,2),则m,n的值为__________.
15.一次函数y=kx+b的图象经过点(0,4),且与两坐标轴所围成的三角形的面积为8,则k=________,b=__________.
三、解答题
16.如图,在直角坐标系中,A(﹣1,3),B(3,﹣2).
(1)求△AOB的面积;
(2)设AB交y轴于点C,求C点的坐标.
(第16题图)
17.如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:
(1)方程kx+b=0的解;
(2)式子k+b的值;
(3)方程kx+b=-3的解.
(第17题图)
18.如图,直线y=﹣x+b与反比例函数的图象相交于点A(a,3),且与x轴相交于点B.
(1)求a、b的值;
(2)若点P在x轴上,且△AOP的面积是△AOB的面积的,求点P的坐标.
(第18题图)
19.在平面直角坐标系中,直线y= -x+2与y轴交于点A,点A关于x轴的对称点为B,过点B作y轴的垂线l,直线l与直线y= -x+2交于点C.
(1)求点B、C的坐标;
(2)若直线y=2x+b与△ABC有两个公共点,求b的取值范围.
(第19题图)
参考答案
一、1.D【解析】∵方程ax+b=0的解是直线y=ax+b与x轴的交点横坐标,∴方程ax+b=0的解是x=-3.故选D.
2.D【解析】当x≤3时,-x+c≥ax+b,即x的不等式-x+c≥ax+b的解集为x≤3.故选D.
3.D【解析】∵直线a与b的交点为P(m,n),∴是方程2x+3y=4、3x+2y=4的解,也是方程组的解,∴A、B、C均正确,D错误.故选D.
4.C【解析】∵直线y=3x+6与直线y=2x+4的交点坐标为(a,b),∴解为的方程组是,即.故选C.
5.C【解析】利用待定系数法分别求出两个一次函数的解析式为和,则所组成的二元一次方程组为.故选C.
6.D【解析】∵直线y=2x+2沿y轴向下平移4个单位,∴平移后解析式为y=2x?2.
当y=0时,0=2x?2,解得x=1.故新直线与x轴的交点坐标是 (1,0).故选D.
7.C【解析】因为的解析式是,为一函数表达式,且直线经过第二、三、四象限,所以根据一次函数的性质,可得, ,即, ;根据数轴的基本概念可知, 项符合题意.故选.
8.C【解析】把代入的,计算得出,则点坐标为,
所以当时, ,即不等式的解集为.故选C.
9.A【解析】当x=?2时,直线y1=k1x+b都在直线y2=k2x的上方,即y1≥y2.故选A.
10.C【解析】∵直线l1:y=x+3与直线l2:y=mx+n交于点A(-1,b),∴当x=-1时,b=-1+3=2,
∴点A的坐标为(-1,2),∴关于x、y的方程组的解是.故选C.
二、11.(0,4)【解析】∵当x=0时,y=4, ∴图象与y轴的交点坐标是(0,4).
12. x<1【解析】由图像可得点P的坐标为(1,-2);不等式的解集是x<1.
13.﹣3【解析】令时,解得,故与轴的交点为.由函数图象可得,当时,函数的图象在轴上方,且其函数图象在函数图象的下方,故解集是,所以关于的不等式的整数解为.
14.(1)1 (2)m=, n=【解析】(1)由题意知,P(0,4-2m),Q(0,m-3) ,所以4-2m+m-3=0,所以m=1.(2)由题意知,(1,2)在两个一次函数上,代入函数有,
解得.
15. ±1 4【解析】一次函数过点(0,4),所以 b=4,一次函数与x轴的交点是(-)则,解得k=±1.
三、16.(1)3.5;(2)(0, ).【解析】由A(﹣1,3),B(3,﹣2)可以求出直线AB的方程,再根据直线方程来求解即可.
解:过AB两点的直线方程为,即4y+5x﹣7=0.
当y=0时,x=,即该直线与x轴的交点是D(,0).
(1)S△AOB=S△AOD+S△BOD
=OD×3+OD×2
=OD×(3+2)
=×5 .即S△AOB=;
(2)当x=0时,y=,即直线4y+5x﹣7=0与x轴的交点C的坐标是(0, ).
(第16题答图)
17.解:(1)如图所示,当y=0时,x=2.故方程kx+b=0的解是x=2;
(2)根据图示知,该直线经过点(2,0)和点(0,-2),则,
解得,
故k+b=1-2=-1,即k+b=-1.
(3)根据图示知,当y=-3时,x=-1.
故方程kx+b=-3的解是x=-1.
18.解:(1)∵直线与反比例函数的图象相交于点A(,3),
∴=-1.∴A(﹣1,3).∴2.
(2)直线与轴相交于点B.∴B(2,0),∵点P在轴上,△AOP的面积是△AOB的面积的,∴OB=2PO,∴P的坐标为(1,0 )或(-1,0 ).
19.解:(1)在y=-x+2中,令x=0得y=2,所以A(0,2),
由此得出点A关于y轴对称点为B(0,-2) .
把y=-2代入y=-x+2中得x=4,所以C(4,2)
(2)-10
一、选择题
1.直线过点和点,则方程的解是( ).
A. B. C. D.
2.如图,直线y=﹣x+c与直线y=ax+b的交点坐标为(3,﹣1),关于x的不等式﹣x+c≥ax+b的解集为( )
(第2题图)
A. x≥﹣1 B. x≤﹣1??? ?C. x≥3???? D. x≤3
3.在平面直角坐标系中,方程2x+3y=4所对应的直线为a,方程3x+2y=4所对应的直线为b,直线a与b的交点为P(m,n),下列说法错误的是( )
A. 是方程2x+3y=4的解 B. 是方程3x+2y=4的解
C. 是方程组的解 D. 以上说法均错误
4.若直线y=3x+6与直线y=2x+4的交点坐标为(a,b),则解为的方程组是( )
A. B.
C. D.
5.如图,以两条直线l1,l2的交点坐标为解的方程组是( )
(第5题图)
A. B.
C. D.
6.直线y=2x+2向下平移4个单位后与x轴的交点坐标是( )
A. (0,1) B. (0,-1) C. (-1,0) D. (1,0)
7.已知一次函数的图象经过第二、三、四象限,则的取值范围在数轴上表示为( ).
A. B.
C. D.
8.如图,正比例函数与一次函数的图象交于点,则不等式的解集为( ).
(第8题图)
A. B. C. D.
9.同一直角坐标系中,一次函数y1=k1x+b与正比例函数y2=k2x的图象如图所示,则满足y1≥y2的x取值范围是( )
(第9题图)
A. x≤﹣2 B. x≥﹣2 C. x<﹣2 D. x>﹣2
10.如图,在平面直角坐标系中,直线l1:y=x+3与直线l2:y=mx+n交于点A(﹣1,b),则关于x、y的方程组的解为( )
(第10题图)
A. B. C. D.
二、填空题
11.一次函数y=-2x+4的图象与y轴的交点坐标是__________。
12.如图,函数与函数的图象交于点P,那么点P的坐标为_______,关于x的不等式的解集是________.
(第12题图)
13.如图,直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2,则关于x的不等式﹣x+m>nx+4n>0的整数解是__________.
(第13题图)
14.已知一次函数y=(n4)x+(42m )和y=(n+1)x+m3.
(1)若它们的图象与y轴的交点分别是点P和点Q.若点P与点Q关于x轴对称,m的值为__________;
(2)若这两个一次函数的图象交于点(1,2),则m,n的值为__________.
15.一次函数y=kx+b的图象经过点(0,4),且与两坐标轴所围成的三角形的面积为8,则k=________,b=__________.
三、解答题
16.如图,在直角坐标系中,A(﹣1,3),B(3,﹣2).
(1)求△AOB的面积;
(2)设AB交y轴于点C,求C点的坐标.
(第16题图)
17.如图,根据函数y=kx+b(k,b是常数,且k≠0)的图象,求:
(1)方程kx+b=0的解;
(2)式子k+b的值;
(3)方程kx+b=-3的解.
(第17题图)
18.如图,直线y=﹣x+b与反比例函数的图象相交于点A(a,3),且与x轴相交于点B.
(1)求a、b的值;
(2)若点P在x轴上,且△AOP的面积是△AOB的面积的,求点P的坐标.
(第18题图)
19.在平面直角坐标系中,直线y= -x+2与y轴交于点A,点A关于x轴的对称点为B,过点B作y轴的垂线l,直线l与直线y= -x+2交于点C.
(1)求点B、C的坐标;
(2)若直线y=2x+b与△ABC有两个公共点,求b的取值范围.
(第19题图)
参考答案
一、1.D【解析】∵方程ax+b=0的解是直线y=ax+b与x轴的交点横坐标,∴方程ax+b=0的解是x=-3.故选D.
2.D【解析】当x≤3时,-x+c≥ax+b,即x的不等式-x+c≥ax+b的解集为x≤3.故选D.
3.D【解析】∵直线a与b的交点为P(m,n),∴是方程2x+3y=4、3x+2y=4的解,也是方程组的解,∴A、B、C均正确,D错误.故选D.
4.C【解析】∵直线y=3x+6与直线y=2x+4的交点坐标为(a,b),∴解为的方程组是,即.故选C.
5.C【解析】利用待定系数法分别求出两个一次函数的解析式为和,则所组成的二元一次方程组为.故选C.
6.D【解析】∵直线y=2x+2沿y轴向下平移4个单位,∴平移后解析式为y=2x?2.
当y=0时,0=2x?2,解得x=1.故新直线与x轴的交点坐标是 (1,0).故选D.
7.C【解析】因为的解析式是,为一函数表达式,且直线经过第二、三、四象限,所以根据一次函数的性质,可得, ,即, ;根据数轴的基本概念可知, 项符合题意.故选.
8.C【解析】把代入的,计算得出,则点坐标为,
所以当时, ,即不等式的解集为.故选C.
9.A【解析】当x=?2时,直线y1=k1x+b都在直线y2=k2x的上方,即y1≥y2.故选A.
10.C【解析】∵直线l1:y=x+3与直线l2:y=mx+n交于点A(-1,b),∴当x=-1时,b=-1+3=2,
∴点A的坐标为(-1,2),∴关于x、y的方程组的解是.故选C.
二、11.(0,4)【解析】∵当x=0时,y=4, ∴图象与y轴的交点坐标是(0,4).
12. x<1【解析】由图像可得点P的坐标为(1,-2);不等式的解集是x<1.
13.﹣3【解析】令时,解得,故与轴的交点为.由函数图象可得,当时,函数的图象在轴上方,且其函数图象在函数图象的下方,故解集是,所以关于的不等式的整数解为.
14.(1)1 (2)m=, n=【解析】(1)由题意知,P(0,4-2m),Q(0,m-3) ,所以4-2m+m-3=0,所以m=1.(2)由题意知,(1,2)在两个一次函数上,代入函数有,
解得.
15. ±1 4【解析】一次函数过点(0,4),所以 b=4,一次函数与x轴的交点是(-)则,解得k=±1.
三、16.(1)3.5;(2)(0, ).【解析】由A(﹣1,3),B(3,﹣2)可以求出直线AB的方程,再根据直线方程来求解即可.
解:过AB两点的直线方程为,即4y+5x﹣7=0.
当y=0时,x=,即该直线与x轴的交点是D(,0).
(1)S△AOB=S△AOD+S△BOD
=OD×3+OD×2
=OD×(3+2)
=×5 .即S△AOB=;
(2)当x=0时,y=,即直线4y+5x﹣7=0与x轴的交点C的坐标是(0, ).
(第16题答图)
17.解:(1)如图所示,当y=0时,x=2.故方程kx+b=0的解是x=2;
(2)根据图示知,该直线经过点(2,0)和点(0,-2),则,
解得,
故k+b=1-2=-1,即k+b=-1.
(3)根据图示知,当y=-3时,x=-1.
故方程kx+b=-3的解是x=-1.
18.解:(1)∵直线与反比例函数的图象相交于点A(,3),
∴=-1.∴A(﹣1,3).∴2.
(2)直线与轴相交于点B.∴B(2,0),∵点P在轴上,△AOP的面积是△AOB的面积的,∴OB=2PO,∴P的坐标为(1,0 )或(-1,0 ).
19.解:(1)在y=-x+2中,令x=0得y=2,所以A(0,2),
由此得出点A关于y轴对称点为B(0,-2) .
把y=-2代入y=-x+2中得x=4,所以C(4,2)
(2)-10
