华师大版八年级数学下册19.3正方形作业设计含答案
文档属性
| 名称 | 华师大版八年级数学下册19.3正方形作业设计含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 150.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览


文档简介
19.3 正方形
一、选择题(12个题,共48分)
1、正方形具有而矩形不具有的性质是( )
A、四个角相等 B、对角线相等 C、对角线垂直 D、对角线互相平分
2、正方形具有而菱形不具有的性质是( )
A、四条边相等 B、是轴对称图形 C、是中心对称图形 D、对角线相等
3、下列叙述中,错误的是( )
A、有一组邻边相等的矩形是正方形 B、有一个角是直角的菱形是正方形
C、对角线垂直平分且相等的四边形是正方形
D、是轴对称也是中心对称是四边形是正方形
4、正方形的周长为12cm,则对角线的长为( )
A、3 cm B、3 cm C、6 cm D、6 cm
5、将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
(第5题图)
A.2 cm2 B.4 cm2 C.6 cm2 D.8 cm2
6、如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,则正方形ABCD的边长为( )
(第6题图)
A.2 B.3 C.4 D.5
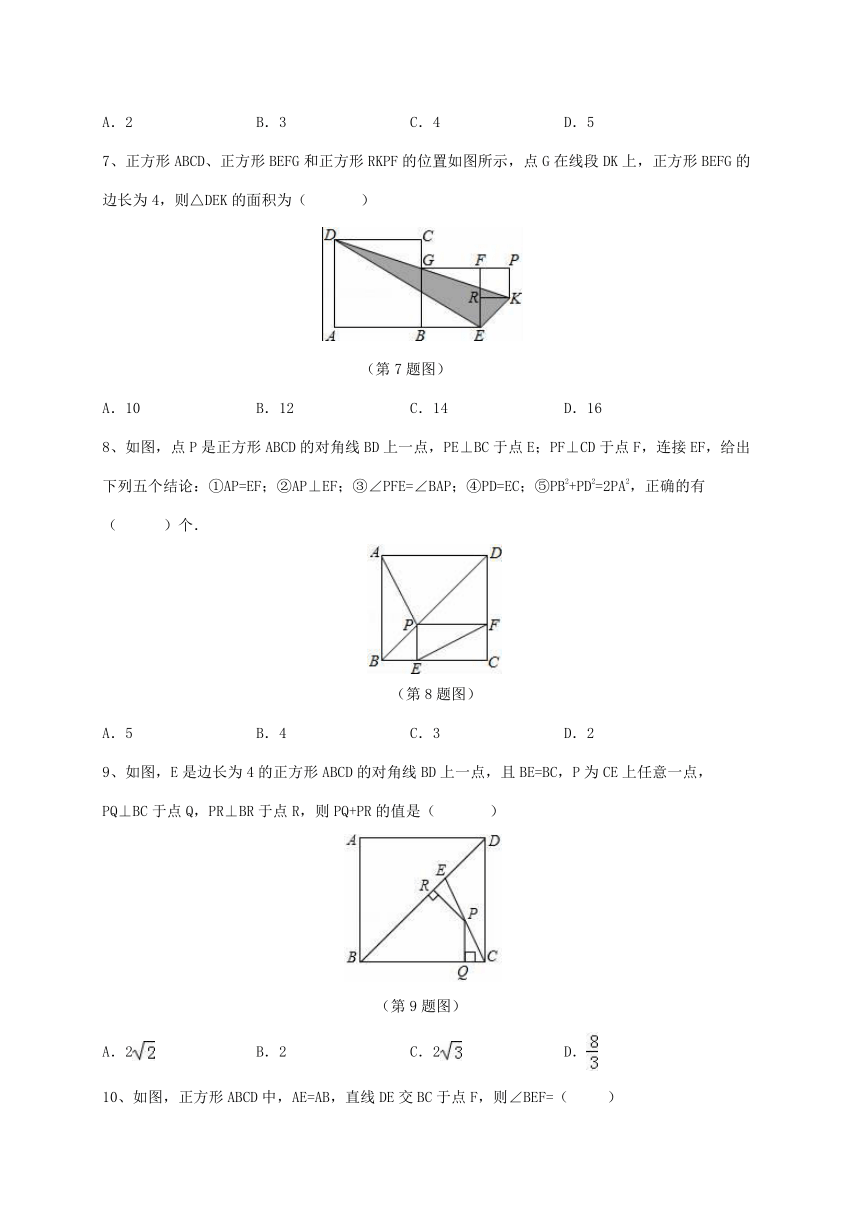
7、正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为( )
(第7题图)
A.10 B.12 C.14 D.16
8、如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E;PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC;⑤PB2+PD2=2PA2,正确的有( )个.
(第8题图)
A.5 B.4 C.3 D.2
9、如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )
(第9题图)
A.2 B.2 C.2 D.
10、如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
(第10题图)
A.35° B.45° C.55° D.60°
11、如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y=(x>0)的图象上,已知点B的坐标是(,),则k的值为( )
(第11题图)
A.4 B.6 C.8 D.10
12、(2014宜兴市校级模拟)如图,在平面直角坐标系中,A(1,0),B(0,3),以AB为边在第一象限作正方形ABCD,点D在双曲线y=(k≠0)上,将正方形沿x轴负方向平移m个单位长度后,点C恰好落在双曲线上,则m的值是( )
(第12题图)
A.2 B.3 C. D.
二、填空题(6个题,共24分)
13、正方形的对角线长为10cm,则正方形的面积为 ;
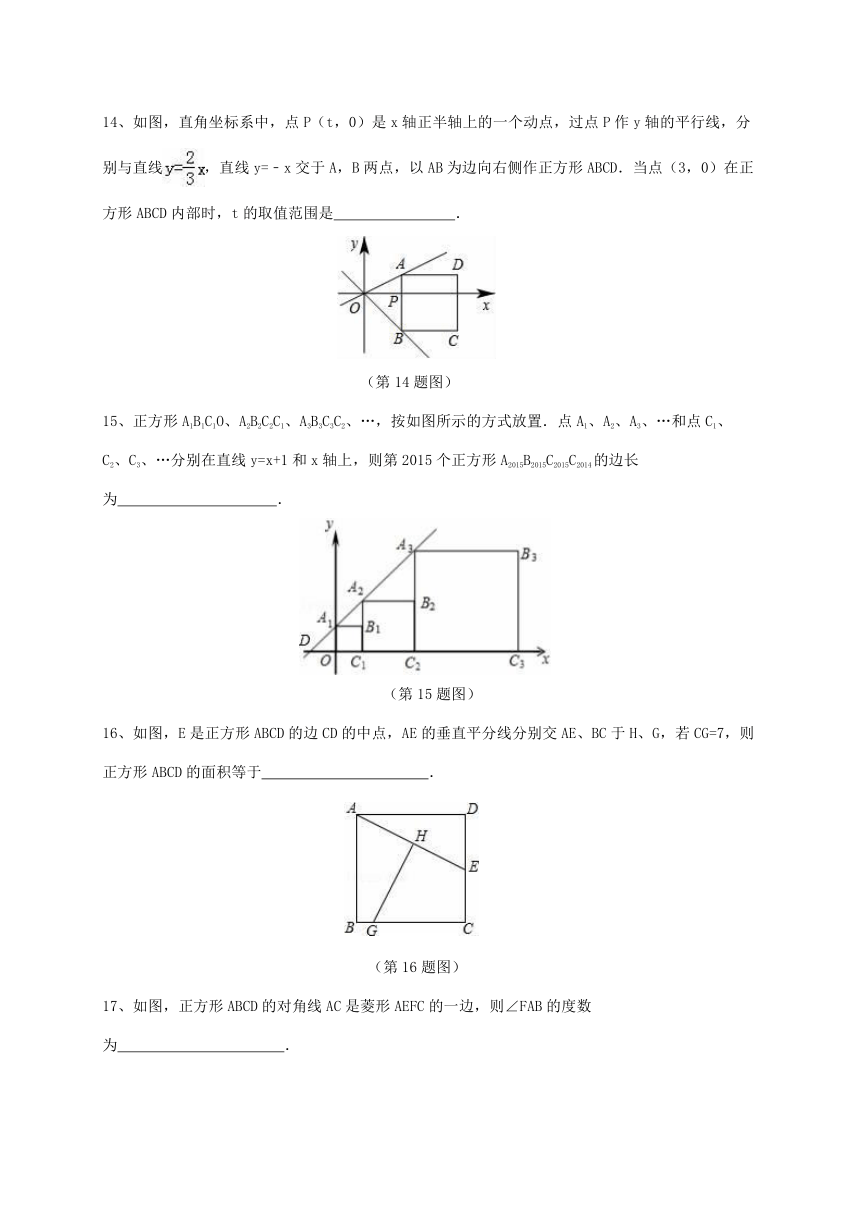
14、如图,直角坐标系中,点P(t,0)是x轴正半轴上的一个动点,过点P作y轴的平行线,分别与直线,直线y=﹣x交于A,B两点,以AB为边向右侧作正方形ABCD.当点(3,0)在正方形ABCD内部时,t的取值范围是 .
(第14题图)
15、正方形A1B1C1O、A2B2C2C1、A3B3C3C2、…,按如图所示的方式放置.点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=x+1和x轴上,则第2015个正方形A2015B2015C2015C2014的边长为 .
(第15题图)
16、如图,E是正方形ABCD的边CD的中点,AE的垂直平分线分别交AE、BC于H、G,若CG=7,则正方形ABCD的面积等于 .
(第16题图)
17、如图,正方形ABCD的对角线AC是菱形AEFC的一边,则∠FAB的度数为 .
(第17题图)
18、如图,在正方形ABCD中,△AEF的顶点E,F分别在BC、CD边上,高AG与正方形的边长相等,连BD分别交AE、AF于点M、N,若EG=4,GF=6,BM=,则MN的长为 .
(第18题图)
三、解答题(5个题,共57分)
19、如图,正方形ABCD中,点E是BC上一点,直线AE交BD于点M,交DC的延长线于点F,G是EF的中点,连结CG.求证:
①△ABM≌△CBM;
②CG⊥CM.
(第19题图)
20、如图,正方形ABCD的边长为6,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G、与对角线BD相交于点H.
(1)若BD=BF,求BE的长;
(2)若∠2=2∠1,求证:HF=HE+HD.
(第20题图)
参考答案
一、1.C 2.D 3.D 4.B 5.B 6.A 7.D 8.B 9.A 10.B 11.C 12.A
二、13. 50cm2 14. <t<3 15.22014 16. 64 17.22.5° 18.
三、19. 证明:①∵四边形ABCD是正方形,
∴AB=CB,∠ABM=∠CBM.
在△ABM和△CBM中,
,
∴△ABM≌△CBM(SAS).
②∵△ABM≌△CBM,
∴∠BAM=∠BCM.
∵∠ECF=90°,G是EF的中点,
∴GC=GF,
∴∠GCF=∠F.
又∵AB∥DF,
∴∠BAM=∠F,
∴∠BCM=∠GCF,
∴∠BCM+∠GCE=∠GCF+∠GCE=90°,
∴GC⊥CM.
(第19题答图)
20. (1)解:∵四边形ABCD是正方形,且FD⊥DE,
∴∠ADE=90°﹣∠EDC=∠CDF,AD=DC,∠A=∠DCF=90°,
在△DAE和△DCF中,
,
∴Rt△DAE≌Rt△DCF(AAS),
∴AE=CF,
∵CF=BF﹣BC=BD﹣BC=6﹣6,
∴BE=AB﹣AE=AB﹣CF=6﹣(6﹣6)=12﹣6;
(2)证明:在HF上取一点P,使FP=EH,连接DP.
由(1)Rt△DAE≌Rt△DCF得△EDF是等腰直角三角形,
∴DE=DF,∠DEF=∠DFE=45°,
∴△DEH≌△DFP(SAS),
∴DH=DP,∠EDH=∠FDP.
在△DHE和△FHB中,
∵∠DEF=∠HBF=45°,∠EHD=∠BHF(对顶角),
∴∠EDH=∠1=∠2=(45°﹣∠EDH),
∴∠EDH=15°,∠FDP=15°,
∴∠HDP=90°﹣15°﹣15°=60°,
∴△DHP是等边三角形,
∴HD=HP,HF=HE+HD.
(第20题图)
一、选择题(12个题,共48分)
1、正方形具有而矩形不具有的性质是( )
A、四个角相等 B、对角线相等 C、对角线垂直 D、对角线互相平分
2、正方形具有而菱形不具有的性质是( )
A、四条边相等 B、是轴对称图形 C、是中心对称图形 D、对角线相等
3、下列叙述中,错误的是( )
A、有一组邻边相等的矩形是正方形 B、有一个角是直角的菱形是正方形
C、对角线垂直平分且相等的四边形是正方形
D、是轴对称也是中心对称是四边形是正方形
4、正方形的周长为12cm,则对角线的长为( )
A、3 cm B、3 cm C、6 cm D、6 cm
5、将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
(第5题图)
A.2 cm2 B.4 cm2 C.6 cm2 D.8 cm2
6、如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为4,则正方形ABCD的边长为( )
(第6题图)
A.2 B.3 C.4 D.5
7、正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为( )
(第7题图)
A.10 B.12 C.14 D.16
8、如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E;PF⊥CD于点F,连接EF,给出下列五个结论:①AP=EF;②AP⊥EF;③∠PFE=∠BAP;④PD=EC;⑤PB2+PD2=2PA2,正确的有( )个.
(第8题图)
A.5 B.4 C.3 D.2
9、如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )
(第9题图)
A.2 B.2 C.2 D.
10、如图,正方形ABCD中,AE=AB,直线DE交BC于点F,则∠BEF=( )
(第10题图)
A.35° B.45° C.55° D.60°
11、如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y=(x>0)的图象上,已知点B的坐标是(,),则k的值为( )
(第11题图)
A.4 B.6 C.8 D.10
12、(2014宜兴市校级模拟)如图,在平面直角坐标系中,A(1,0),B(0,3),以AB为边在第一象限作正方形ABCD,点D在双曲线y=(k≠0)上,将正方形沿x轴负方向平移m个单位长度后,点C恰好落在双曲线上,则m的值是( )
(第12题图)
A.2 B.3 C. D.
二、填空题(6个题,共24分)
13、正方形的对角线长为10cm,则正方形的面积为 ;
14、如图,直角坐标系中,点P(t,0)是x轴正半轴上的一个动点,过点P作y轴的平行线,分别与直线,直线y=﹣x交于A,B两点,以AB为边向右侧作正方形ABCD.当点(3,0)在正方形ABCD内部时,t的取值范围是 .
(第14题图)
15、正方形A1B1C1O、A2B2C2C1、A3B3C3C2、…,按如图所示的方式放置.点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=x+1和x轴上,则第2015个正方形A2015B2015C2015C2014的边长为 .
(第15题图)
16、如图,E是正方形ABCD的边CD的中点,AE的垂直平分线分别交AE、BC于H、G,若CG=7,则正方形ABCD的面积等于 .
(第16题图)
17、如图,正方形ABCD的对角线AC是菱形AEFC的一边,则∠FAB的度数为 .
(第17题图)
18、如图,在正方形ABCD中,△AEF的顶点E,F分别在BC、CD边上,高AG与正方形的边长相等,连BD分别交AE、AF于点M、N,若EG=4,GF=6,BM=,则MN的长为 .
(第18题图)
三、解答题(5个题,共57分)
19、如图,正方形ABCD中,点E是BC上一点,直线AE交BD于点M,交DC的延长线于点F,G是EF的中点,连结CG.求证:
①△ABM≌△CBM;
②CG⊥CM.
(第19题图)
20、如图,正方形ABCD的边长为6,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G、与对角线BD相交于点H.
(1)若BD=BF,求BE的长;
(2)若∠2=2∠1,求证:HF=HE+HD.
(第20题图)
参考答案
一、1.C 2.D 3.D 4.B 5.B 6.A 7.D 8.B 9.A 10.B 11.C 12.A
二、13. 50cm2 14. <t<3 15.22014 16. 64 17.22.5° 18.
三、19. 证明:①∵四边形ABCD是正方形,
∴AB=CB,∠ABM=∠CBM.
在△ABM和△CBM中,
,
∴△ABM≌△CBM(SAS).
②∵△ABM≌△CBM,
∴∠BAM=∠BCM.
∵∠ECF=90°,G是EF的中点,
∴GC=GF,
∴∠GCF=∠F.
又∵AB∥DF,
∴∠BAM=∠F,
∴∠BCM=∠GCF,
∴∠BCM+∠GCE=∠GCF+∠GCE=90°,
∴GC⊥CM.
(第19题答图)
20. (1)解:∵四边形ABCD是正方形,且FD⊥DE,
∴∠ADE=90°﹣∠EDC=∠CDF,AD=DC,∠A=∠DCF=90°,
在△DAE和△DCF中,
,
∴Rt△DAE≌Rt△DCF(AAS),
∴AE=CF,
∵CF=BF﹣BC=BD﹣BC=6﹣6,
∴BE=AB﹣AE=AB﹣CF=6﹣(6﹣6)=12﹣6;
(2)证明:在HF上取一点P,使FP=EH,连接DP.
由(1)Rt△DAE≌Rt△DCF得△EDF是等腰直角三角形,
∴DE=DF,∠DEF=∠DFE=45°,
∴△DEH≌△DFP(SAS),
∴DH=DP,∠EDH=∠FDP.
在△DHE和△FHB中,
∵∠DEF=∠HBF=45°,∠EHD=∠BHF(对顶角),
∴∠EDH=∠1=∠2=(45°﹣∠EDH),
∴∠EDH=15°,∠FDP=15°,
∴∠HDP=90°﹣15°﹣15°=60°,
∴△DHP是等边三角形,
∴HD=HP,HF=HE+HD.
(第20题图)
