人教版数学七年级下册 5.2.2 平行线的判定 同步课时练习题 含答案
文档属性
| 名称 | 人教版数学七年级下册 5.2.2 平行线的判定 同步课时练习题 含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 188.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览


文档简介
第五章 相交线与平行线 5.2 平行线及其判定 5.2.2 平行线的判定
1. 如图,下列推理错误的是( )
A.∵∠1=∠3,∴a∥b B.∵∠3=∠4,∴c∥d
C.∵∠1=∠2,∴c∥d D.∵∠1=∠4,∴a∥b
2. 如图,下列说法中,正确的是( )
A.因为∠A+∠D=180°,所以AD∥BC
B.因为∠C+∠D=180°,所以AB∥CD
C.因为∠A+∠D=180°,所以AB∥CD
D.因为∠A+∠C=180°,所以AB∥CD
3. 如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠5=180°,则a∥c
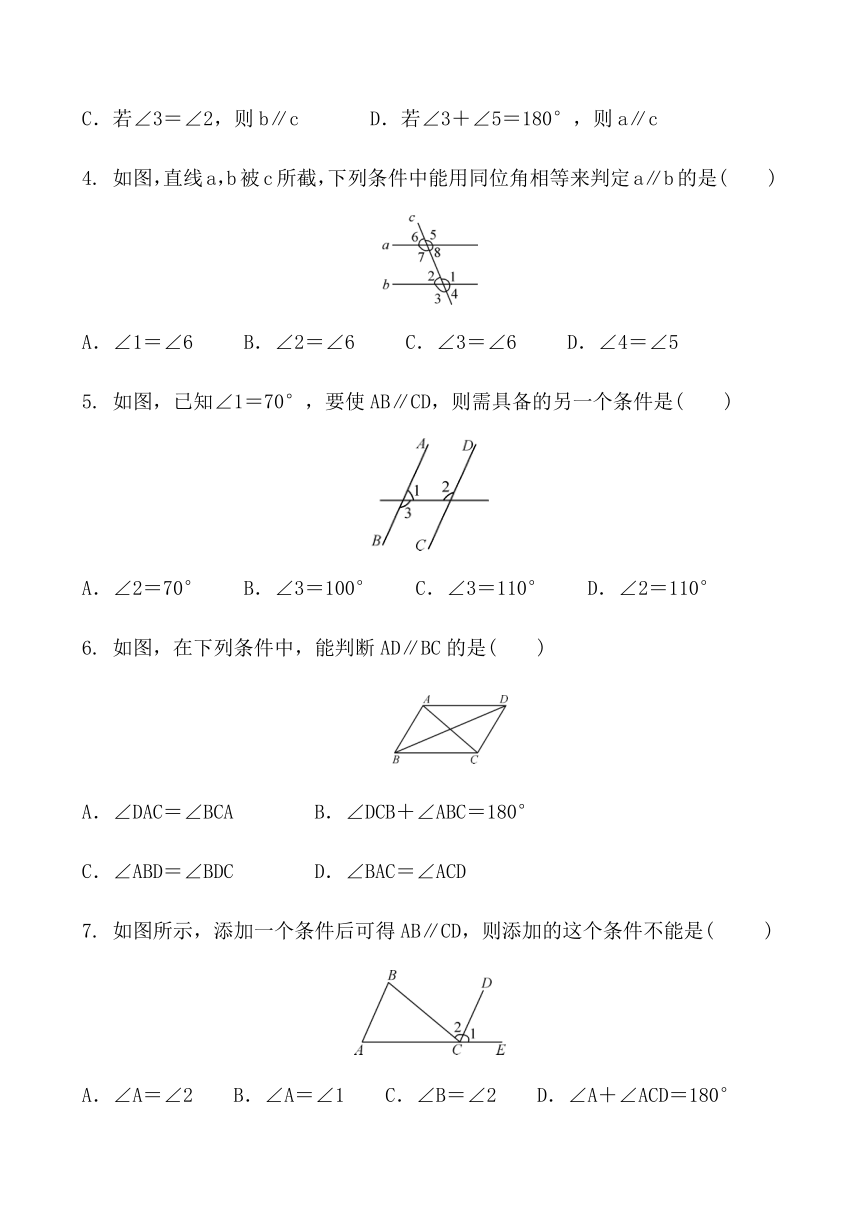
4. 如图,直线a,b被c所截,下列条件中能用同位角相等来判定a∥b的是( )
A.∠1=∠6 B.∠2=∠6 C.∠3=∠6 D.∠4=∠5
5. 如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是( )
A.∠2=70° B.∠3=100° C.∠3=110° D.∠2=110°
6. 如图,在下列条件中,能判断AD∥BC的是( )
A.∠DAC=∠BCA B.∠DCB+∠ABC=180°
C.∠ABD=∠BDC D.∠BAC=∠ACD
7. 如图所示,添加一个条件后可得AB∥CD,则添加的这个条件不能是( )
A.∠A=∠2 B.∠A=∠1 C.∠B=∠2 D.∠A+∠ACD=180°
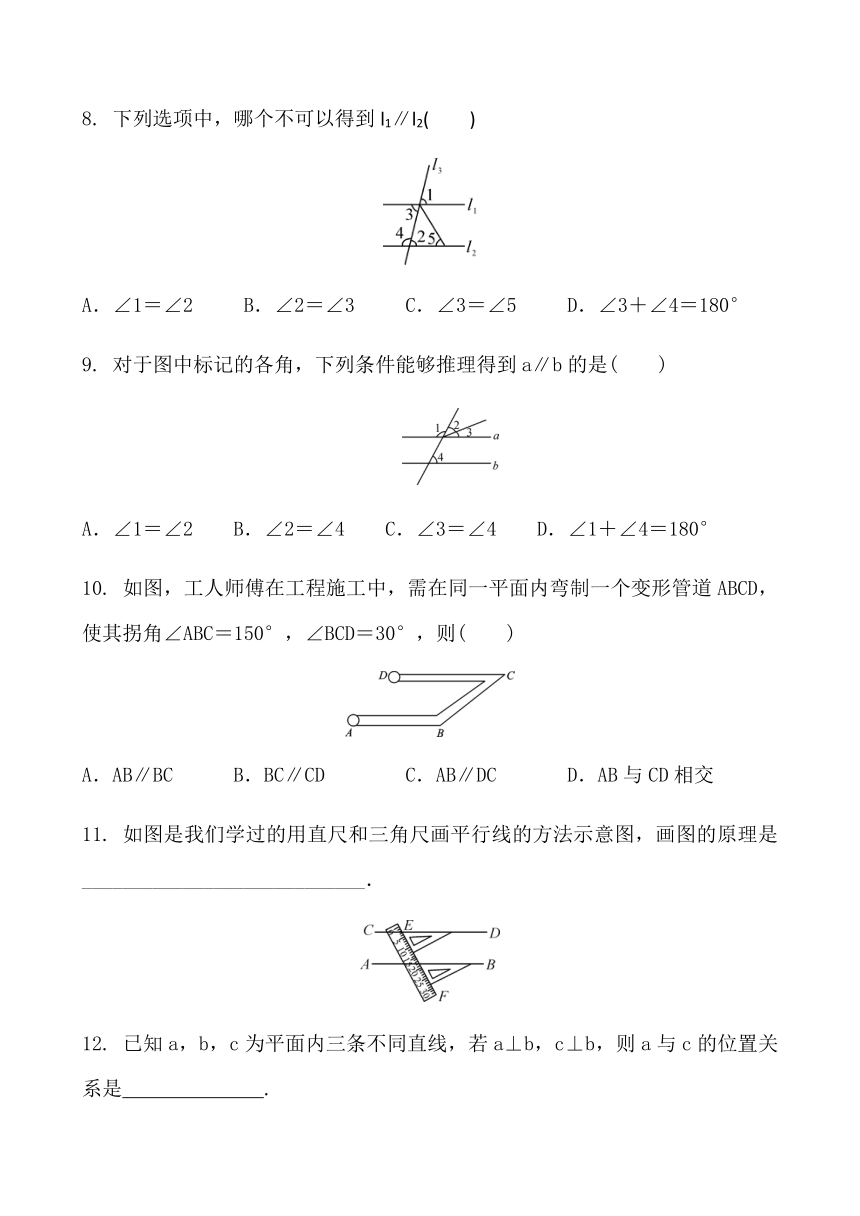
8. 下列选项中,哪个不可以得到l1∥l2( )
A.∠1=∠2 B.∠2=∠3 C.∠3=∠5 D.∠3+∠4=180°
9. 对于图中标记的各角,下列条件能够推理得到a∥b的是( )
A.∠1=∠2 B.∠2=∠4 C.∠3=∠4 D.∠1+∠4=180°
10. 如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
A.AB∥BC B.BC∥CD C.AB∥DC D.AB与CD相交
11. 如图是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是____________________________.
12. 已知a,b,c为平面内三条不同直线,若a⊥b,c⊥b,则a与c的位置关系是 .
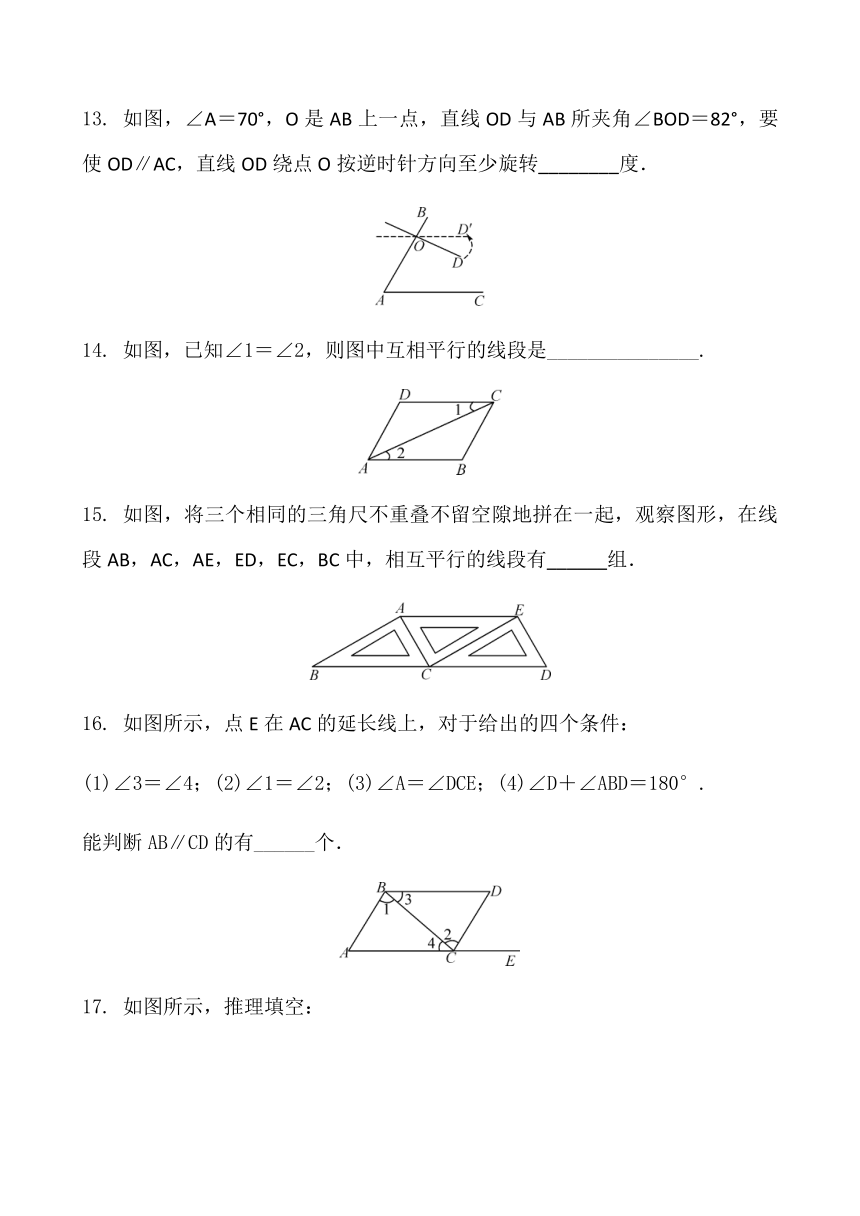
13. 如图,∠A=70°,O是AB上一点,直线OD与AB所夹角∠BOD=82°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转________度.
14. 如图,已知∠1=∠2,则图中互相平行的线段是_______________.
15. 如图,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB,AC,AE,ED,EC,BC中,相互平行的线段有______组.
16. 如图所示,点E在AC的延长线上,对于给出的四个条件:
(1)∠3=∠4;(2)∠1=∠2;(3)∠A=∠DCE;(4)∠D+∠ABD=180°.
能判断AB∥CD的有______个.
17. 如图所示,推理填空:
(1)∵∠1= (已知),
∴AC∥ED(同位角相等,两直线平行).
(2)∵∠2= (已知),
∴AB∥FD(内错角相等,两直线平行).
(3)∵∠2+ =180°(已知),
∴AC∥ED(同旁内角互补,两直线平行).
18. 如图,∠1=120°,∠C=60°,判断AB与CD是否平行?为什么?
19. 如图,已知∠ACD=70°,∠ACB=60°,∠ABC=50°,试说明:AB∥CD.
20. 如图,已知CD平分∠ACB,∠1=∠2,试判断AC与DE的位置关系,并说明理由.
21. 如图所示,回答下列问题:
(1)∠1=∠2,能得到哪两条直线平行?说明理由;
(2)能否得到BF∥DE?若不能,还需要添加一个什么条件?
22. 如图,∠B=45°,∠BED=75°,∠D=30°,猜想AB与CD有怎样的位置关系?并说明理由.
23. 如图,直线EF分别与直线AB,CD相交于点P和点Q,PG平分∠APQ,QH平分∠DQP,并且∠1=∠2,说出图中哪些直线平行,并说明理由.
答案:
1—10 ACCBD AACDC
11. 同位角相等,两直线平行
12. 平行
13. 12
14. AB∥CD
15. 3
16. 3
17. (1)∠C
(2)∠BED
(3)∠AFD
18. 解:AB∥CD.理由:∵∠1=120°,∴∠2=∠1=120°.∵∠C=60°,∴∠2+∠C=180°,∴AB∥CD.
19. 解:∵∠ACD=70°,∠ACB=60°,∴∠BCD=∠ACD+∠ACB=70°+60°=130°.∵∠ABC=50°,∴∠BCD+∠ABC=130°+50°=180°,∴AB∥CD.
20. 解:AC∥DE,理由:∵CD平分∠ACB,∴∠1=∠ACD.∵∠1=∠2,∴∠ACD=∠2,∴AC∥DE.
21. 解:(1)能得到AB∥CD.理由:由∠1=∠2,内错角相等,两直线平行,得到AB∥CD
.(2)不能得到BF∥DE.需添加的条件是∠1=∠EDF(答案不唯一).
22. 解:AB∥CD.理由:在∠BED内作∠BEF=45°,则∠B=∠BEF=45°,∴AB∥EF.∵∠BED=75°,∴∠FED=∠BED-∠BEF=75°-45°=30°,∴∠FED=∠D=30°,∴EF∥CD,∴AB∥CD.
23. 解:PG∥QH,AB∥CD.
∵PG平分∠APQ,QH平分∠DQP,∴∠1=∠GPQ=∠APQ,∠PQH=∠2=∠PQD.
又∵∠1=∠2,∴∠GPQ=∠PQH,∠APQ=∠PQD.∴PG∥QH,AB∥CD.
