(新版)青岛版八年级数学下册第11章图形的平移与旋转检测卷(含答案)
文档属性
| 名称 | (新版)青岛版八年级数学下册第11章图形的平移与旋转检测卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 390.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 21:56:34 | ||
图片预览

文档简介
第11章 单元检测卷
(时间:90分钟 满分:100分)
一、选择题(共10小题,每小题3分,共30分)
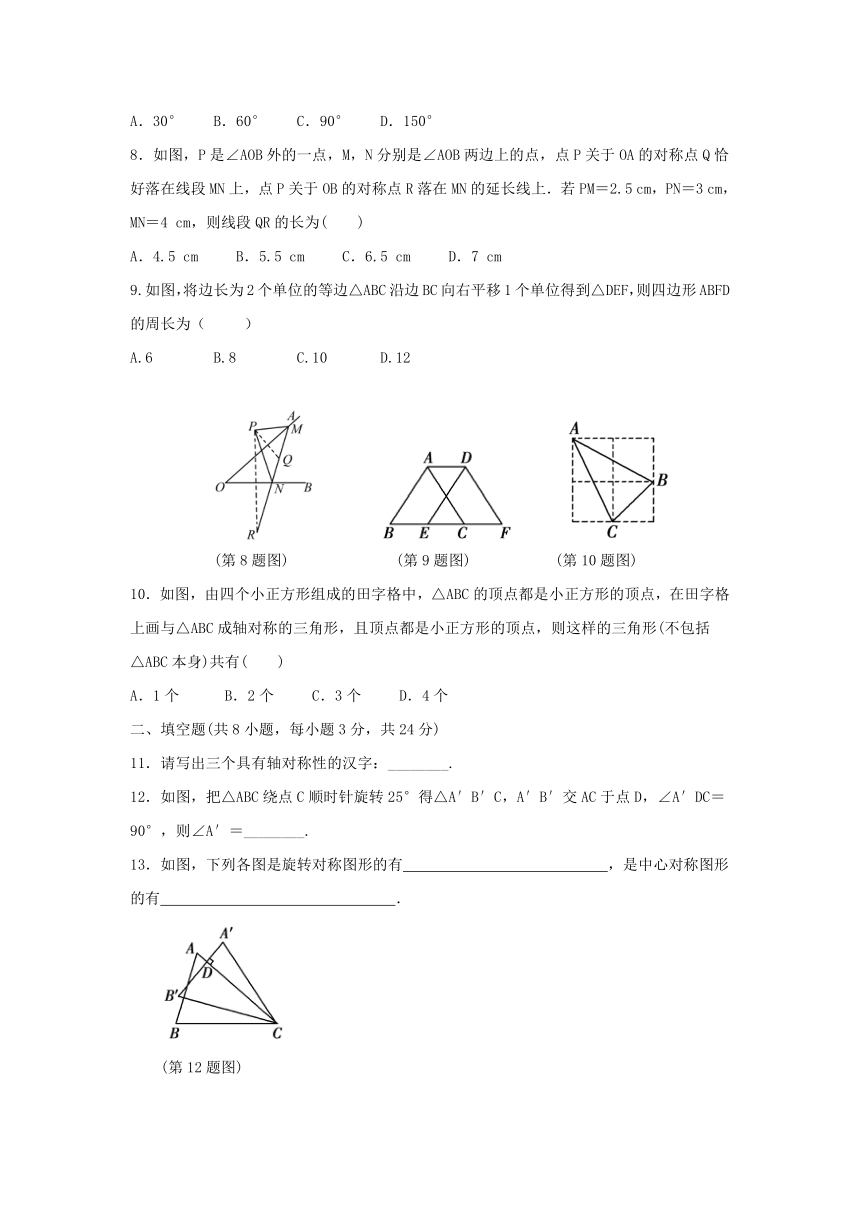
1.下列图形,既是轴对称图形,又是中心对称图形的是( )
2.下列各网格中的图形是用其图形中的一部分平移得到的是( )
3.如图,△ABC经过平移到达△DEF的位置,则下列四个说法,正确的有( )
①AB∥DE,AB=DE;②AD∥BE∥CF,AD=BE=CF;
③AC∥DF,AC=DF;④BC∥EF,BC=EF.
A.1个 B.2个 C.3个 D.4个
4.如图,是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A.150° B.180° C.210° D.120°
5.如图,在下列四种图形变换中,该图案不包含的变换是( )
A.平移 B.轴对称 C.旋转 D.中心对称
(第4题图) (第5题图) (第7题图)
6.如图,如果甲、乙两图关于点O成中心对称,则乙图不符合题意的一块是( )
7.如图,在直角三角形△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为( )
A.30° B.60° C.90° D.150°
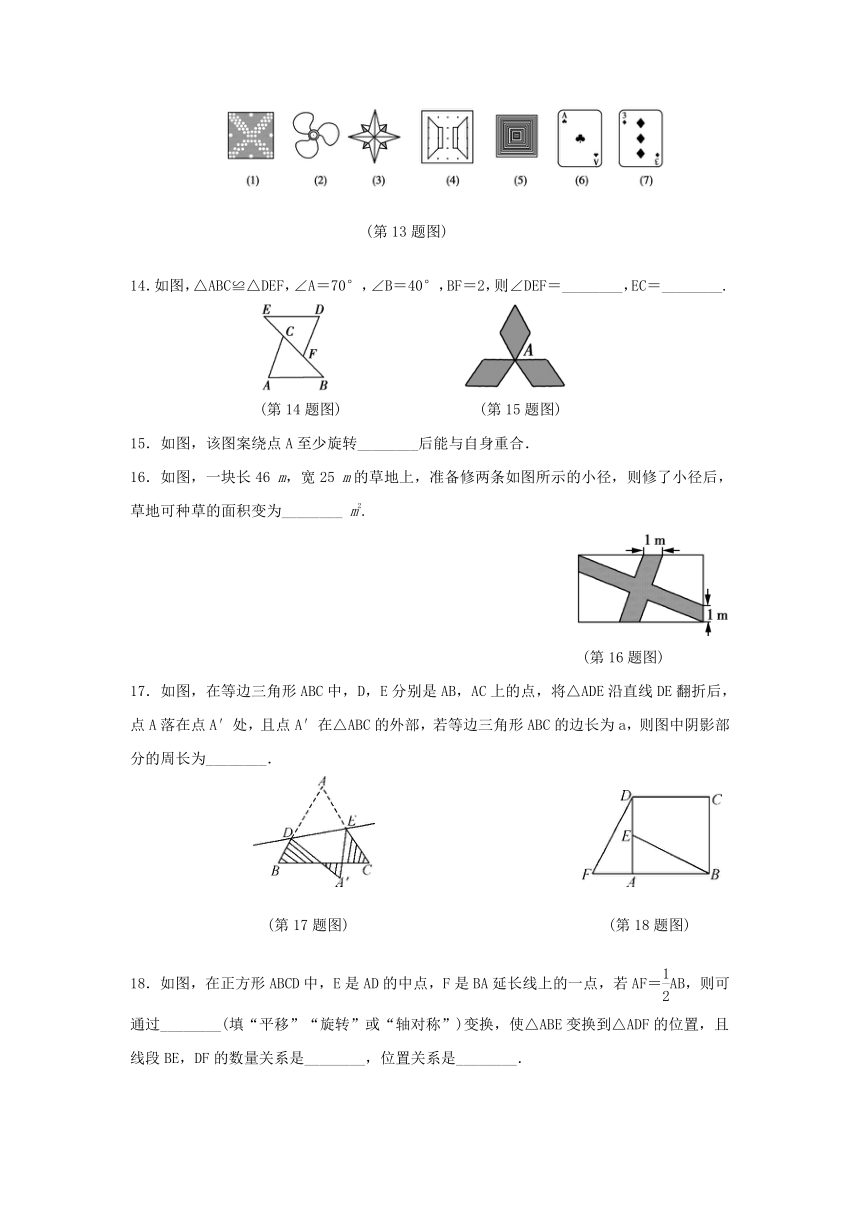
8.如图,P是∠AOB外的一点,M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若PM=2.5 cm,PN=3 cm,MN=4 cm,则线段QR的长为( )
A.4.5 cm B.5.5 cm C.6.5 cm D.7 cm
9.如图,将边长为2个单位的等边△ABC沿边BC向右平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12
(第8题图) (第9题图) (第10题图)
10.如图,由四个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点,在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包括△ABC本身)共有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共8小题,每小题3分,共24分)
11.请写出三个具有轴对称性的汉字:________.
12.如图,把△ABC绕点C顺时针旋转25°得△A′B′C,A′B′交AC于点D,∠A′DC=90°,则∠A′=________.
13.如图,下列各图是旋转对称图形的有 ,是中心对称图形的有 .
(第12题图)
(第13题图)
14.如图,△ABC≌△DEF,∠A=70°,∠B=40°,BF=2,则∠DEF=________,EC=________.
(第14题图) (第15题图)
15.如图,该图案绕点A至少旋转________后能与自身重合.
16.如图,一块长46 m,宽25 m的草地上,准备修两条如图所示的小径,则修了小径后,草地可种草的面积变为________ m2.
(第16题图)
17.如图,在等边三角形ABC中,D,E分别是AB,AC上的点,将△ADE沿直线DE翻折后,点A落在点A′处,且点A′在△ABC的外部,若等边三角形ABC的边长为a,则图中阴影部分的周长为________.
(第17题图) (第18题图)
18.如图,在正方形ABCD中,E是AD的中点,F是BA延长线上的一点,若AF=AB,则可通过________(填“平移”“旋转”或“轴对称”)变换,使△ABE变换到△ADF的位置,且线段BE,DF的数量关系是________,位置关系是________.
三、解答题(共6小题,共46分)
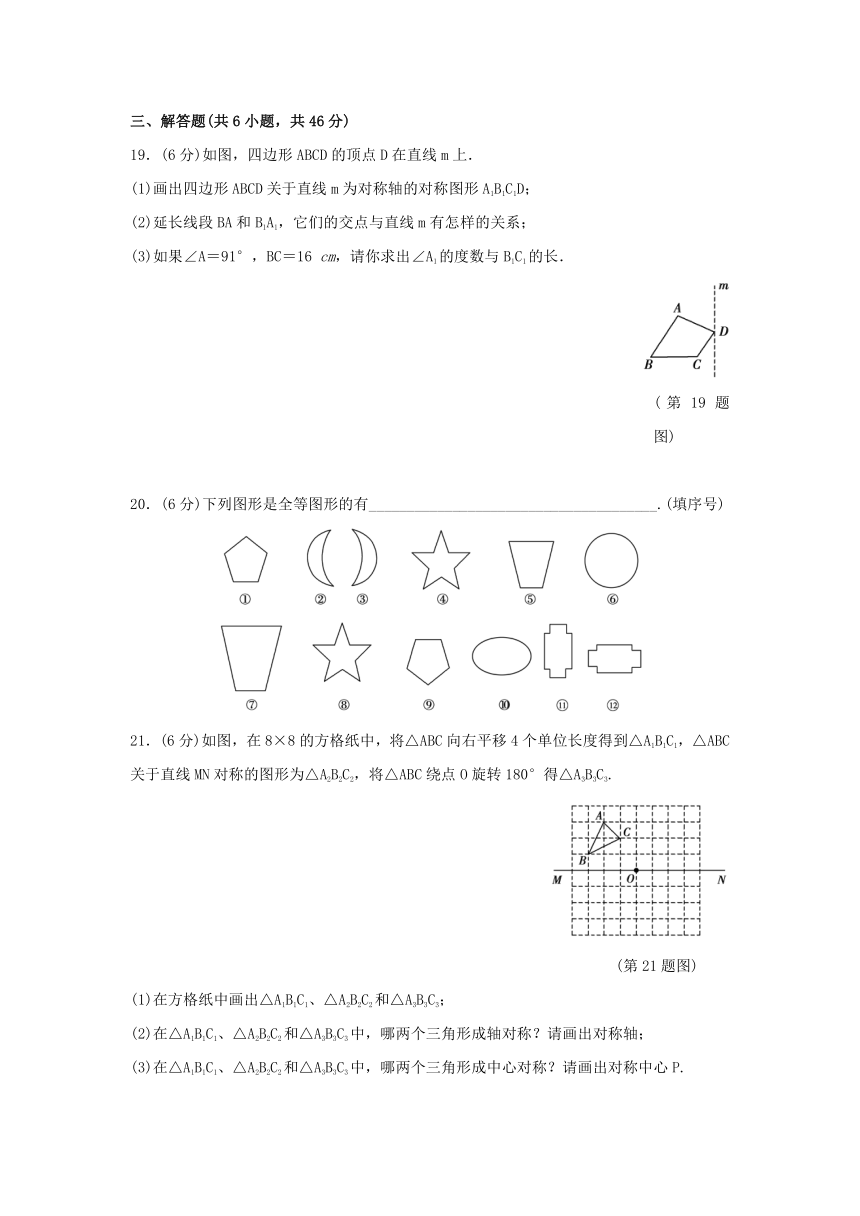
19.(6分)如图,四边形ABCD的顶点D在直线m上.
(1)画出四边形ABCD关于直线m为对称轴的对称图形A1B1C1D;
(2)延长线段BA和B1A1,它们的交点与直线m有怎样的关系;
(3)如果∠A=91°,BC=16 cm,请你求出∠A1的度数与B1C1的长.
(第19题图)
20.(6分)下列图形是全等图形的有______________________________________.(填序号)
21.(6分)如图,在8×8的方格纸中,将△ABC向右平移4个单位长度得到△A1B1C1,△ABC关于直线MN对称的图形为△A2B2C2,将△ABC绕点O旋转180°得△A3B3C3.
(第21题图)
(1)在方格纸中画出△A1B1C1、△A2B2C2和△A3B3C3;
(2)在△A1B1C1、△A2B2C2和△A3B3C3中,哪两个三角形成轴对称?请画出对称轴;
(3)在△A1B1C1、△A2B2C2和△A3B3C3中,哪两个三角形成中心对称?请画出对称中心P.
22.(8分)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
(第22题图)
(1)画出一个格点△A1B1C1,使它与△ABC全等且点A与点A1是对应点;
(2)画出点B关于直线AC的对称点D,并指出AD可以看作由AB绕A点经过怎样的旋转而得到的.
23.(8分)认真观察前四个图中阴影部分构成的图案(每个小正方形的边长都为1),回答下列问题:
(第23题图)
(1)请写出这四个图案都具有的三个共同特征:
特征1:_________________________________;
特征2:_____________________________________________;
特征3:___________________________________________.
(2)请在第五个图中设计出你心中最美丽的图案,使它也具备你所写出的上述特征.
24.(12分)学完图形的全等后,数学老师出了一道题:“如图,已知△ABC≌△ADE,∠BAD=40°,∠C=50°,问DE与AC有何位置关系,并说明理由.”请你完成这道题.
(第24题图)
参考答案
一、1---10 CCDBA CBABC
二、11. 甲、由、中、田、日等
12. 65°
13. (1)(2)(3)(4)(5)(7) (1)(3)(4)(5)(7)
14. 40° 2
15. 120°
16. 1 080
17. 3a
18. 旋转 BE=DF BE⊥DF
三、19. (1)画图略;
(2)交点在直线m上;
(3)∠A1=91°,B1C1=16 cm.
20. ①与⑨,②与③,④与⑧,?与?.
21. (1)画图略;
(2)△A2B2C2与△A3B3C3成轴对称;
(3)△A1B1C1与△A3B3C3成中心对称,对称中心点P为A1A3的垂直平分线与B1B3的垂直平分线的交点.
22.
(第22题答图)
(1) 本题是开放题,答案不唯一,图中给出了两个满足条件的三角形,其他解答只要正确即可;
(2) D点如图所示,AD是由AB绕A点逆时针旋转90°而得到的,或AD是由AB绕A点顺时针旋转270°而得到的
23. (1) 都是中心对称图形,都是轴对称图形,面积都是4.
(2) 画图略.
24. DE⊥AC.
理由:∵△ABC≌△ADE,∴∠BAC=∠DAE,∠E=∠C=50°,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,∴∠CAE=40°,∴∠AFE=180°-∠CAE-∠E=90°.
(时间:90分钟 满分:100分)
一、选择题(共10小题,每小题3分,共30分)
1.下列图形,既是轴对称图形,又是中心对称图形的是( )
2.下列各网格中的图形是用其图形中的一部分平移得到的是( )
3.如图,△ABC经过平移到达△DEF的位置,则下列四个说法,正确的有( )
①AB∥DE,AB=DE;②AD∥BE∥CF,AD=BE=CF;
③AC∥DF,AC=DF;④BC∥EF,BC=EF.
A.1个 B.2个 C.3个 D.4个
4.如图,是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A.150° B.180° C.210° D.120°
5.如图,在下列四种图形变换中,该图案不包含的变换是( )
A.平移 B.轴对称 C.旋转 D.中心对称
(第4题图) (第5题图) (第7题图)
6.如图,如果甲、乙两图关于点O成中心对称,则乙图不符合题意的一块是( )
7.如图,在直角三角形△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为( )
A.30° B.60° C.90° D.150°
8.如图,P是∠AOB外的一点,M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若PM=2.5 cm,PN=3 cm,MN=4 cm,则线段QR的长为( )
A.4.5 cm B.5.5 cm C.6.5 cm D.7 cm
9.如图,将边长为2个单位的等边△ABC沿边BC向右平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12
(第8题图) (第9题图) (第10题图)
10.如图,由四个小正方形组成的田字格中,△ABC的顶点都是小正方形的顶点,在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包括△ABC本身)共有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共8小题,每小题3分,共24分)
11.请写出三个具有轴对称性的汉字:________.
12.如图,把△ABC绕点C顺时针旋转25°得△A′B′C,A′B′交AC于点D,∠A′DC=90°,则∠A′=________.
13.如图,下列各图是旋转对称图形的有 ,是中心对称图形的有 .
(第12题图)
(第13题图)
14.如图,△ABC≌△DEF,∠A=70°,∠B=40°,BF=2,则∠DEF=________,EC=________.
(第14题图) (第15题图)
15.如图,该图案绕点A至少旋转________后能与自身重合.
16.如图,一块长46 m,宽25 m的草地上,准备修两条如图所示的小径,则修了小径后,草地可种草的面积变为________ m2.
(第16题图)
17.如图,在等边三角形ABC中,D,E分别是AB,AC上的点,将△ADE沿直线DE翻折后,点A落在点A′处,且点A′在△ABC的外部,若等边三角形ABC的边长为a,则图中阴影部分的周长为________.
(第17题图) (第18题图)
18.如图,在正方形ABCD中,E是AD的中点,F是BA延长线上的一点,若AF=AB,则可通过________(填“平移”“旋转”或“轴对称”)变换,使△ABE变换到△ADF的位置,且线段BE,DF的数量关系是________,位置关系是________.
三、解答题(共6小题,共46分)
19.(6分)如图,四边形ABCD的顶点D在直线m上.
(1)画出四边形ABCD关于直线m为对称轴的对称图形A1B1C1D;
(2)延长线段BA和B1A1,它们的交点与直线m有怎样的关系;
(3)如果∠A=91°,BC=16 cm,请你求出∠A1的度数与B1C1的长.
(第19题图)
20.(6分)下列图形是全等图形的有______________________________________.(填序号)
21.(6分)如图,在8×8的方格纸中,将△ABC向右平移4个单位长度得到△A1B1C1,△ABC关于直线MN对称的图形为△A2B2C2,将△ABC绕点O旋转180°得△A3B3C3.
(第21题图)
(1)在方格纸中画出△A1B1C1、△A2B2C2和△A3B3C3;
(2)在△A1B1C1、△A2B2C2和△A3B3C3中,哪两个三角形成轴对称?请画出对称轴;
(3)在△A1B1C1、△A2B2C2和△A3B3C3中,哪两个三角形成中心对称?请画出对称中心P.
22.(8分)如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
(第22题图)
(1)画出一个格点△A1B1C1,使它与△ABC全等且点A与点A1是对应点;
(2)画出点B关于直线AC的对称点D,并指出AD可以看作由AB绕A点经过怎样的旋转而得到的.
23.(8分)认真观察前四个图中阴影部分构成的图案(每个小正方形的边长都为1),回答下列问题:
(第23题图)
(1)请写出这四个图案都具有的三个共同特征:
特征1:_________________________________;
特征2:_____________________________________________;
特征3:___________________________________________.
(2)请在第五个图中设计出你心中最美丽的图案,使它也具备你所写出的上述特征.
24.(12分)学完图形的全等后,数学老师出了一道题:“如图,已知△ABC≌△ADE,∠BAD=40°,∠C=50°,问DE与AC有何位置关系,并说明理由.”请你完成这道题.
(第24题图)
参考答案
一、1---10 CCDBA CBABC
二、11. 甲、由、中、田、日等
12. 65°
13. (1)(2)(3)(4)(5)(7) (1)(3)(4)(5)(7)
14. 40° 2
15. 120°
16. 1 080
17. 3a
18. 旋转 BE=DF BE⊥DF
三、19. (1)画图略;
(2)交点在直线m上;
(3)∠A1=91°,B1C1=16 cm.
20. ①与⑨,②与③,④与⑧,?与?.
21. (1)画图略;
(2)△A2B2C2与△A3B3C3成轴对称;
(3)△A1B1C1与△A3B3C3成中心对称,对称中心点P为A1A3的垂直平分线与B1B3的垂直平分线的交点.
22.
(第22题答图)
(1) 本题是开放题,答案不唯一,图中给出了两个满足条件的三角形,其他解答只要正确即可;
(2) D点如图所示,AD是由AB绕A点逆时针旋转90°而得到的,或AD是由AB绕A点顺时针旋转270°而得到的
23. (1) 都是中心对称图形,都是轴对称图形,面积都是4.
(2) 画图略.
24. DE⊥AC.
理由:∵△ABC≌△ADE,∴∠BAC=∠DAE,∠E=∠C=50°,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,∴∠CAE=40°,∴∠AFE=180°-∠CAE-∠E=90°.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
