北师大版七年级数学下册第二章 相交线与平行线 专题练习(含答案)
文档属性
| 名称 | 北师大版七年级数学下册第二章 相交线与平行线 专题练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 456.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览



文档简介
第二章 相交线与平行线 专题练习
一、选择题
1.下列说法中正确的个数有( )
①两点之间的所有连线中,线段最短;
②相等的角叫对顶角;
③过一点有且只有一条直线与已知直线平行;
④过一点有且只有一条直线与已知直线垂直;
⑤两点之间的距离是两点间的线段;
⑥在同一平面内,两条直线的位置关系只有两种:平行或相交.
A.1个 B.2个 C.3个 D.4个
2.如图,AB∥CD,AD=CD,∠1=50°,则∠2的度数是( )
A.55° B.60° C.65° D.70°
3.如图,直线a∥b,将一块含30°角(∠BAC=30°)的直角三角尺按图中方式放置,其中A和C两点分别落在直线a和b上.若∠1=20°,则∠2的度数为( )
A.20° B.30° C.40° D.50°
4.如图,直线AB,CD相交于点O,OD平分∠BOF,OE⊥CD于点O.若∠EOF=α,下列说法:①∠AOC=α-90° ②∠EOB=180°-α ③∠AOF=360°-2α,其中正确的是( )
A.①② B.①③
C.②③ D.①②③
5.如图,AB∥CD,∠B=75°,∠E=27°,则∠D的度数为( )
A.45° B.48° C.50° D.58°
6.如图,点E是BA延长线上一点,在下列条件中:①∠1=∠3 ②∠2=∠4 ③∠5=∠D ④∠BAD=∠BCD ⑤∠B+∠BCD=180°,能判定AB∥DC的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,小明从A处出发,沿北偏东40°方向行走至B处,又从点B处沿东偏南20°方向行走至C处,则∠ABC等于( )
A.130° B.120° C.110° D.100°
二、填空题
8.如图,∠AOB的一边OA为平面镜,∠AOB=37°,在OB上有一点E,从点E射出一束光线经OA上一点D反射,此时∠ODE=∠ADC,且反射光线DC恰好与OB平行,则∠DEB的度数是__________.
,
9.如图,将一条直的等宽纸带按如图的方式折叠时,则图中∠α=____________.
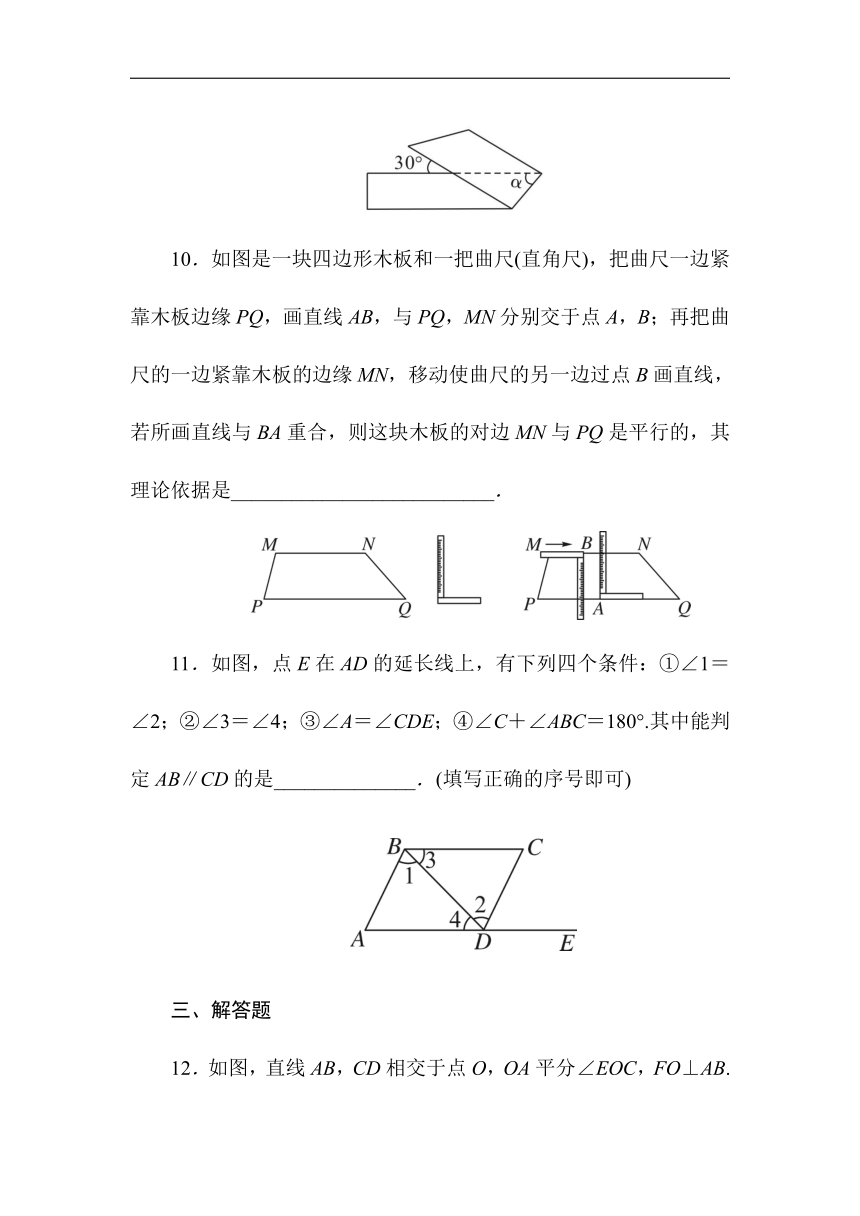
10.如图是一块四边形木板和一把曲尺(直角尺),把曲尺一边紧靠木板边缘PQ,画直线AB,与PQ,MN分别交于点A,B;再把曲尺的一边紧靠木板的边缘MN,移动使曲尺的另一边过点B画直线,若所画直线与BA重合,则这块木板的对边MN与PQ是平行的,其理论依据是__________________________.
11.如图,点E在AD的延长线上,有下列四个条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠C+∠ABC=180°.其中能判定AB∥CD的是______________.(填写正确的序号即可)
三、解答题
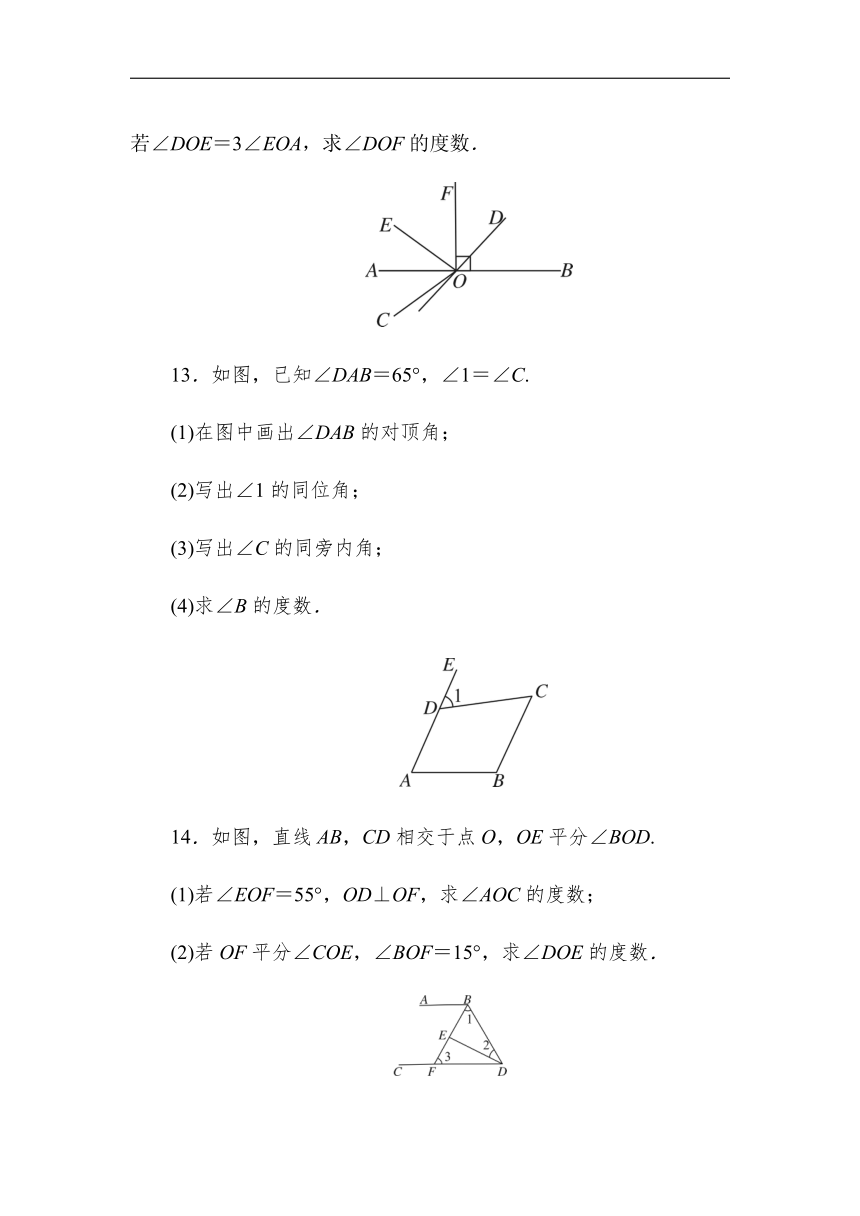
12.如图,直线AB,CD相交于点O,OA平分∠EOC,FO⊥AB.若∠DOE=3∠EOA,求∠DOF的度数.
13.如图,已知∠DAB=65°,∠1=∠C.
(1)在图中画出∠DAB的对顶角;
(2)写出∠1的同位角;
(3)写出∠C的同旁内角;
(4)求∠B的度数.
14.如图,直线AB,CD相交于点O,OE平分∠BOD.
(1)若∠EOF=55°,OD⊥OF,求∠AOC的度数;
(2)若OF平分∠COE,∠BOF=15°,求∠DOE的度数.
15.如图:已知∠1+∠2=180°,∠3=∠B,问AB与DE是否平行?并说明理由.
16.
【阅读材料】在“相交线与平行线”的学习中,有这样一道典型问题:
如图①,AB∥CD,点P在AB与CD之间,可得结论:∠BAP+∠APC+∠PCD=360°.
理由如下:
过点P作PQ∥AB.
∴∠BAP+∠APQ=180°.
∵AB∥CD,
∴PQ∥CD.
∴∠PCD+∠CPQ=180°.
∴∠BAP+∠APC+∠PCD
=∠BAP+∠APQ+∠CPQ+∠PCD
=180°+180°
=360°.
【问题解决】
(1)如图②,AB∥CD,点P在AB与CD之间,可得∠BAP,∠APC,∠PCD间的等量关系是______________________(只写结论);
(2)如图③,AB∥CD,点P,E在AB与CD之间,AE平分∠BAP,CE平分∠DCP.写出∠AEC与∠APC间的等量关系,并写出理由;
结论:∠APC=2∠AEC.
理由:图③中,设∠EAB=∠EAP=x,∠ECD=∠ECP=y.
由(1)可知:∠AEC=x+y,∠APC=2x+2y,
∴∠APC=2∠AEC.
(3)如图④,AB∥CD,点P,E在AB与CD之间,∠BAE=∠BAP,∠DCE=∠DCP,可得∠AEC与∠APC间的等量关系是__________________________(只写结论).
参考答案
一、选择题
1. A
提示:①正确,②③④⑤⑥错误.
2. C
3. C
4. D
5. B
6. C
7. C
二、填空题
8. 74°
9. 75°
10. 内错角相等,两直线平行
11. ①③④
三、解答题
12.
解: 设∠AOE=x°.
∵OA平分∠EOC,∴∠AOC=∠AOE=x°.
∵∠DOE=3∠EOA,∴∠DOE=3x°.
∵∠BOD=∠AOC=x°,
∴由∠AOE+∠DOE+∠BOD=180°,
得x+3x+x=180,解得x=36,
∴∠BOD=36°.
∵FO⊥AB,∴∠BOF=90°,
∴∠DOF=∠BOF-∠BOD=54°.
13.
解: (1)如答图,∠GAH即为所求.
(2)∠1的同位角是∠DAB.
(3)∠C的同旁内角是∠B和∠ADC.
(4)∵∠1=∠C,∴AE∥BC,
∴∠DAB+∠B=180°.
又∵∠DAB=65°,∴∠B=115°.
14.
解: (1)∵OE平分∠BOD,
∴∠BOE=∠DOE.
∵∠EOF=55°,OD⊥OF,
∴∠DOE=35°,
∴∠BOD=70°,
∴∠AOC=70°.
(2)∵OF平分∠COE,∴∠COF=∠EOF.
设∠DOE=∠BOE=x.
∵∠BOF=15°,∴∠COF=∠EOF=x+15°.
∵∠COD=∠COF+∠EOF+∠DOE=180°,
∴x+15°+x+15°+x=180°,解得x=50°,
故∠DOE的度数为50°.
15.
解: AB∥DE.
理由:∵∠1+∠ADC=180°(平角的定义),
且∠1+∠2=180°(已知),
∴∠ADC=∠2(等量代换),
∴EF∥DC(同位角相等,两直线平行).
∴∠3=∠EDC(两直线平行,内错角相等),
又∵∠3=∠B(已知),
∴∠EDC=∠B(等量代换),
∴AB∥DE(同位角相等,两直线平行).
16.
(1) ∠APC=∠A+∠C
(2)
结论:∠APC=2∠AEC.
理由:图③中,设∠EAB=∠EAP=x,∠ECD=∠ECP=y.
由(1)可知:∠AEC=x+y,∠APC=2x+2y,
∴∠APC=2∠AEC.
(3) ∠APC+3∠AEC=360°
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
