(新版)青岛版八年级数学下册第6章平行四边形检测卷含答案
文档属性
| 名称 | (新版)青岛版八年级数学下册第6章平行四边形检测卷含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 22:04:24 | ||
图片预览




文档简介
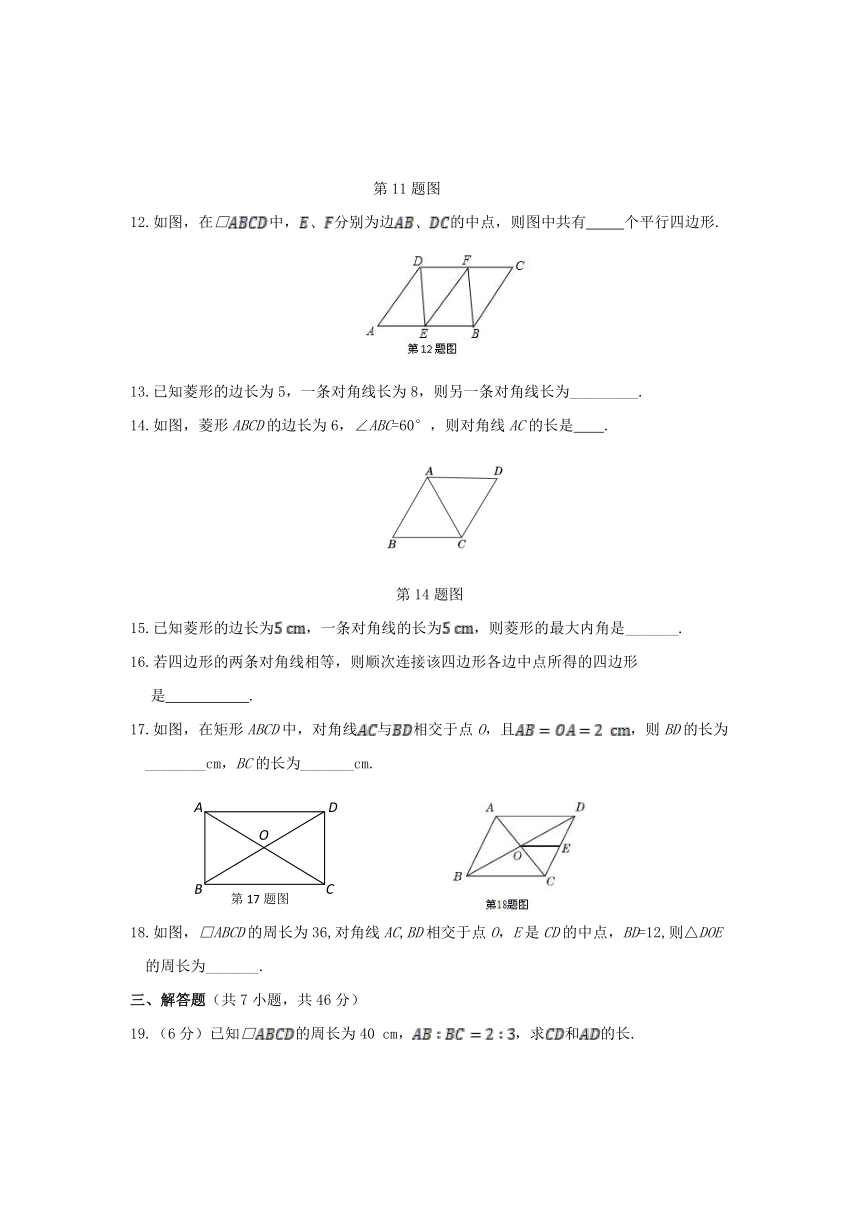
第6章 单元检测卷
(时间:90分钟 满分:100分)
一、选择题(每小题3分,共10小题,共30分)
1.如图,在平行四边形中,,,的垂直平分线交于点,则△的周长是( )
A.6 B.8 C.9 D.10
2.如图,已知□的周长是,△ABC的周长是,则的长为( )
A. B. C. D.
3.如图,在□ABCD中,AD=2AB,CE平分∠BCD交AD边于点E, 且AE=3,则AB的长为( )
A.4 B.3 C. D.2
4.如图,将矩形ABCD沿对角线BD折叠,使点C与点C′重合.若AB=2,则C′D的长为( )
A.1 B.2 C.3 D.4
5.如图,在矩形中,分别为边的中点.若,
,则图中阴影部分的面积为( )
A.3 B.4 C.6 D.8
6.如图为菱形与△重叠的情形,其中在上.若,,,则( )
A.8 B.9 C.11 D.12
7.下列命题中,真命题的个数是( )
①对角线互相平分的四边形是平行四边形.
②两组对角分别相等的四边形是平行四边形.
③一组对边平行,另一组对边相等的四边形是平行四边形.
A.3 B.2 C.1 D.0
8.如图,在□ABCD中,下列结论一定正确的是( )
A.AC⊥BD B.∠A+∠B=180° C.AB=AD D.∠A≠∠C
9.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF.添加一个条件,仍不能证明四边形BECF为正方形的是( )
A.BC=AC B.CF⊥BF C.BD=DF D.AC=BF
10.如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化.下列判断错误的是( )
A.四边形ABCD由矩形变为平行四边形
B. BD的长度增大
C.四边形ABCD的面积不变
D.四边形ABCD的周长不变
二、填空题(每小题3分,共8小题,共24分)
11.如图,在等腰梯形ABCD中,AD∥BC, BC=50,AB=20,∠B=60°,则AD=_______.
第11题图
12.如图,在□中,分别为边的中点,则图中共有 个平行四边形.
13.已知菱形的边长为5,一条对角线长为8,则另一条对角线长为_________.
14.如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长是 .
第14题图
15.已知菱形的边长为,一条对角线的长为,则菱形的最大内角是_______.
16.若四边形的两条对角线相等,则顺次连接该四边形各边中点所得的四边形是 .
17.如图,在矩形ABCD中,对角线与相交于点O,且 ,则BD的长为________cm,BC的长为_______cm.
18.如图,□ABCD的周长为36,对角线AC,BD相交于点O,E是CD的中点,BD=12,则△DOE的周长为_______.
三、解答题(共7小题,共46分)
19.(6分)已知□的周长为40 cm,,求和的长.
20.(6分)已知,在□中,∠的平分线分成和两条线段,求□的周长.
21. (6分)嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图的四边形ABCD,并写出了如下不完整的已知和求证.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇的想法写出证明;
(3)用文字叙述所证命题的逆命题为_______________________________
第21题图
22.(6分)如图,在矩形中,相交于点,平分交于点.若,求∠的度数.
23.(6分)如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.
(1)求证:△ABG≌△AFG;
(2)求BG的长.
第23题图
24.(7分)如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
25.(9分)已知:如图,四边形是菱形,过的中点作的垂线,交于点,
交的延长线于点.
(1)求证:.
(2)若,求菱形的周长.
参考答案
一、1.B 解析:
2.D 解析:因为□的周长是28 cm,所以 .因为△的周长是,所以 .
3.B 解析:∵ CE平分∠BCD,∴ ∠BCE=∠DCE.∵ 四边形ABCD是平行四边形,∴ AD∥BC.∴ ∠DEC=∠BCE.∴ ∠DCE=∠DEC.∴ CD=DE. ∴ AD=2AB=2CD=2DE. ∴ DE=AE=3.∴ AB=CD=DE=3.
4.B 解析:因为四边形ABCD是矩形,所以CD=AB=2.由于沿BD折叠后点C与点C′重合,所以C′D=CD=2.
5.B 解析:因为矩形ABCD的面积为2×4=8,S△BEH=×1×2=1,所以阴影部分的面积为,故选B.
6.D 解析:连接,设交于点.因为四边形为菱形,所以,且.在△中,因为,所以.在△中,因为,所以.又因为,所以.故选D.
7. B 解析:因为对角线互相平分的四边形是平行四边形,所以①正确;因为两组对角分别相等的四边形是平行四边形,所以②正确;因为一组对边平行且相等的四边形是平行四边形,所以③错误.故正确的是①②.
8.B 解析:平行四边形的对角线互相平分但不一定垂直,所以选项A错误;平行四边形的邻角互补,所以选项B正确;平行四边形的对边相等但邻边不一定相等,所以选项C错误;平行四边形的对角相等,所以∠A=∠C,所以选项D错误.
9.D 解析:因为EF垂直平分BC,所以BE=EC,BF=FC.又BE=BF,所以BE=EC=CF=FB,所以四边形BECF为菱形.如果BC=AC,那么∠ABC=90°÷2=45°,则∠EBF=90°,能证明四边形BECF为正方形.如果CF⊥BF,那么∠BFC=90°,能证明四边形BECF为正方形.如果BD=DF,那么BC=EF,能证明四边形BECF为正方形.当AC=BF时,可得AC=BE=EC=AE,此时∠ABC=30°,则∠EBF=60°,不能证明四边形BECF为正方形.
10. C 解析:在向右扭动框架的过程中,AB与BC不再垂直,但始终有AD=BC,AB=CD,所以四边形ABCD会由矩形变为平行四边形,BD的长度会增大.因为四边形的边长不变,所以四边形周长不变.BC的长不变,但四边形的高将逐渐变小,所以四边形的面积将会变小.
二、11. 30 解析:如图,过点D作DE∥AB交BC于点E,因为AD∥BC,
所以四边形ABED为平行四边形,所以AD=BE,DE=AB.
因为梯形ABCD为等腰梯形,所以AB=DC.所以DE=DC.
因为DE∥AB,所以∠DEC=∠B=60°,
所以△DEC为等边三角形,
所以EC=DC=20.
因为BC=50,所以AD=BE=30. 第11题答图
12.4 解析:因为 在□ABCD中,E、F分别为边AB、DC的中点,
所以 .又因为AB∥CD,所以四边形AEFD,CFEB,DFBE都是平行四边形,再加上□ABCD本身,共有4个平行四边形,故答案为4.
13.6 解析:因为菱形的两条对角线互相垂直平分,根据勾股定理,可求得另一条对角线的一半为3,则另一条对角线长为6.
14. 6 解析:因为四边形ABCD是菱形,所以AB=BC=6.又因为∠ABC=60°,
所以△ABC是等边三角形,所以AC=AB=BC=6..
15.120° 解析:已知菱形的边长为5 cm,一条对角线的长为5 cm,则菱形的相邻两条边与它的一条对角线构成的三角形是等边三角形,即长为5 cm的对角线所对的角是60°,根据菱形的性质得到菱形的另一个内角是120°,即菱形的最大内角是120°.
16.菱形 解析:由四边形的两条对角线相等,知顺次连接该四边形各边中点所得的四边形的四条边相等,即所得四边形是菱形.
17.4 解析:因为 cm,所以 cm.
又因为 ,所以 cm.
,所以(cm).
18.15 解析:∵ E,O分别是CD,BD的中点,∴ OE是△DBC的一条中位线,∴ OE=BC,∴ △DOE的周长为OE+DE+OD=BC+CD+BD= (BC+CD)+6=□ABCD的周长+6=15.
三、19.解:因为四边形是平行四边形,所以,.
设 cm, cm,
又因为平行四边形的周长为40 cm,
所以,解得,
所以 , .
20.解:设∠的平分线交于点,如图.
因为∥,所以∠∠.
又因为∠∠,所以∠∠,所以.
而.
①当时,,
□的周长为;
②当时,
□的周长为.
所以□的周长为或.
21. 解:(1)CD 平行
(2)证明:连接BD.
在△ABD和△CDB中,
∵ AB=CD,AD=CB,BD=DB,
∴ △ABD≌△CDB. 第21题答图
∴ ∠1=∠2,∠3=∠4.
∴ AB∥CD,AD∥CB.
∴ 四边形ABCD是平行四边形.
(3)平行四边形的对边相等.
22.解:因为 平分,所以.
又因为,所以
因为,所以△为等边三角形,所以
因为,
所以△为等腰直角三角形,所以.
所以,,,此时.
23. (1)证明:∵ 四边形ABCD是正方形,∴ ∠B=∠D=90°,AD=AB.
由折叠的性质可知AD=AF,∠AFE=∠D=90°,∴ ∠AFG=90°,AB=AF,
∴ ∠AFG=∠B=90°.又∵AG=AG,∴ △ABG≌△AFG(HL).
(2)解:∵ △ABG≌△AFG,∴ BG=FG.
设BG=FG=x,则GC=6-x.
∵ E为CD的中点,∴ CE=DE=EF=3,∴ EG=x+3.
在Rt△ECG中,,
即,解得x=2.
∴ BG的长为2.
24.证明:(1)∵ BD平分∠ABC,∴ ∠ABD=∠CBD.
又∵ BA=BC,BD=BD,∴ △ABD≌△CBD.
∴ ∠ADB=∠CDB.
(2)∵ PM⊥AD,PN⊥CD,∴ ∠PMD=∠PND=90°.
又∵ ∠ADC=90°,∴ 四边形MPND是矩形.
由(1)知∠ADB=∠CDB,又∵PM⊥AD,PN⊥CD,∴ PM=PN.
∴ 四边形MPND是正方形.
25.(1)证明:因为四边形是菱形,所以.
又因为,所以是的垂直平分线,所以.
因为,所以.
(2)解:因为∥,所以.
因为所以.
又因为,所以,所以△是等腰三角形,
所以,所以,
所以菱形的周长是.
第2题图
A
B
C
D
第1题图
A
B
C
D
E
A
B
C
D
O
第17题图
已知:如图,在四边形ABCD中,BC=AD,
AB=_________.
求证:四边形ABCD是________四边形.
第25题图
A
B
E
D
C
F
M
E
第20题答图
A
D
C
B
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
