冀教版八年级数学下册第十九章平面直角坐标系检测卷含答案
文档属性
| 名称 | 冀教版八年级数学下册第十九章平面直角坐标系检测卷含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 260.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览



文档简介
第十九章 单元检测卷
一.选择题
1.如图,正方形ABCD的边长为4,点A的坐标为(﹣1,1),AB平行于x轴,则点C的坐标为( )
(第1题图)
A.(3,1) B.(﹣1,1) C.(3,5) D.(﹣1,5)
2.若点A(3﹣m,n+2)关于原点的对称点B的坐标是(﹣3,2),则m,n的值为( )
A.m=﹣6,n=﹣4 B.m=0,n=﹣4 C.m=6,n=4 D.m=6,n=﹣4
3.P1(x1,y1),P2(x2,y2)是平面直角坐标系中的任意两点,我们把|x1﹣x2|+|y1﹣y2|叫做P1,P2两点间的“直角距离”,记作d(P1,P2).比如:点P(2,﹣4),Q(1,0),则d(P,Q)=|2﹣1|+|﹣4﹣0|=5,已知Q(2,1),动点P(x,y)满足d(P,Q)=3,且x、y均为整数,则满足条件的点P有( )个.
A.4 B.8 C.10 D.12
4.平面直角坐标系中,点A(﹣3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )
A.6,(﹣3,4) B.2,(3,2) C.2,(3,0) D.1,(4,2)
5.平面直角坐标系中,将三角形各点的纵坐标都减去﹣3,横坐标保持不变,所得图形与原图形相比( )
A.向上平移了3个单位 B.向下平移了3个单位
C.向右平移了3个单位 D.向左平移了3个单位
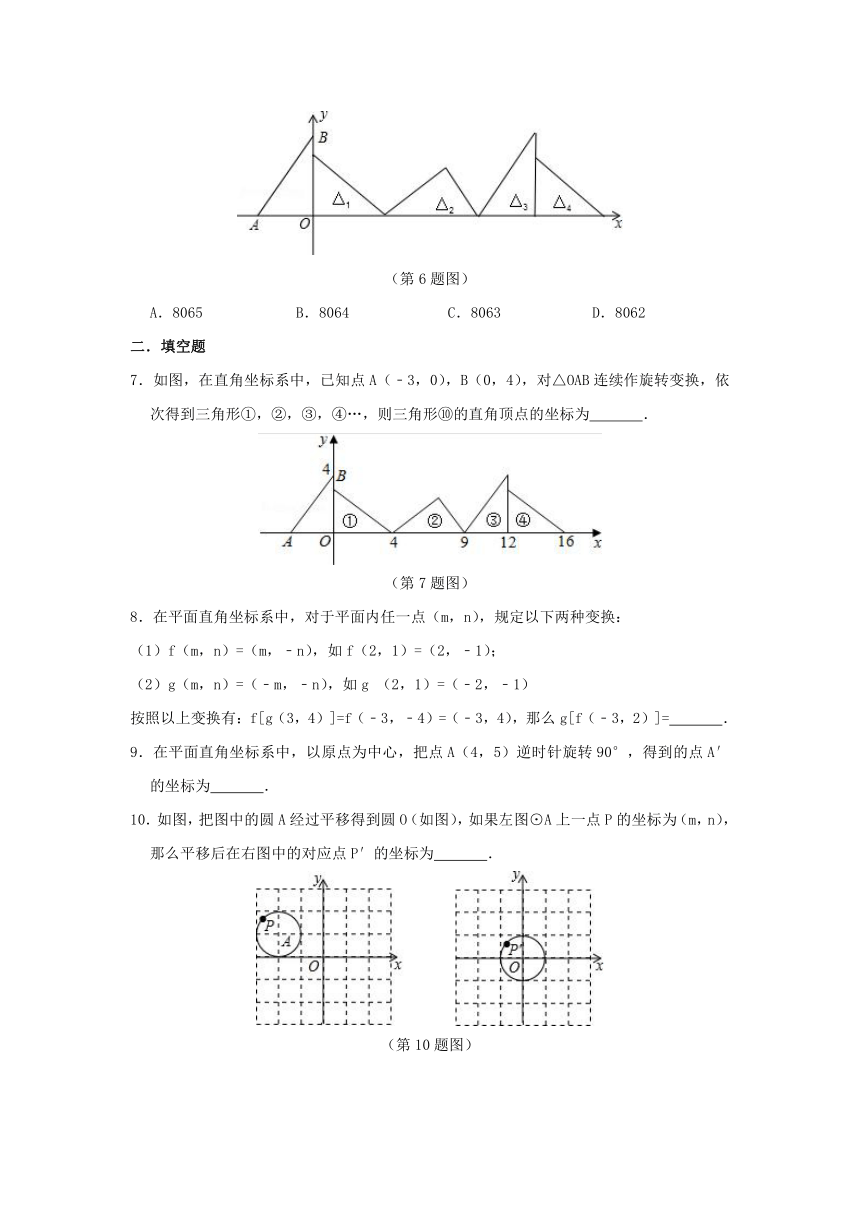
6.如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2016的直角顶点的横坐标为( )
(第6题图)
A.8065 B.8064 C.8063 D.8062
二.填空题
7.如图,在直角坐标系中,已知点A(﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到三角形①,②,③,④…,则三角形⑩的直角顶点的坐标为 .
(第7题图)
8.在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:
(1)f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);
(2)g(m,n)=(﹣m,﹣n),如g (2,1)=(﹣2,﹣1)
按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣3,2)]= .
9.在平面直角坐标系中,以原点为中心,把点A(4,5)逆时针旋转90°,得到的点A′的坐标为 .
10.如图,把图中的圆A经过平移得到圆O(如图),如果左图⊙A上一点P的坐标为(m,n),那么平移后在右图中的对应点P′的坐标为 .
(第10题图)
11.如图,△ABO是关于x轴对称的轴对称图形,点A的坐标为(1,﹣2),则点B的坐标为 .
(第11题图)
12.如图是一组密码的一部分,为了保密,许多情况下课采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“正做数学”的真实意思是“祝你成功”.若“正”所处的位置为(x,y),你找到的密码钥匙是 ,破译的“今天考试”真实意思是 .
(第12题图)
13.在平面直角坐标系xOy中,已知点A(2,﹣2),在y轴上确定点P,使△AOP为等腰三角形,则符合条件的有 个.
三.解答题
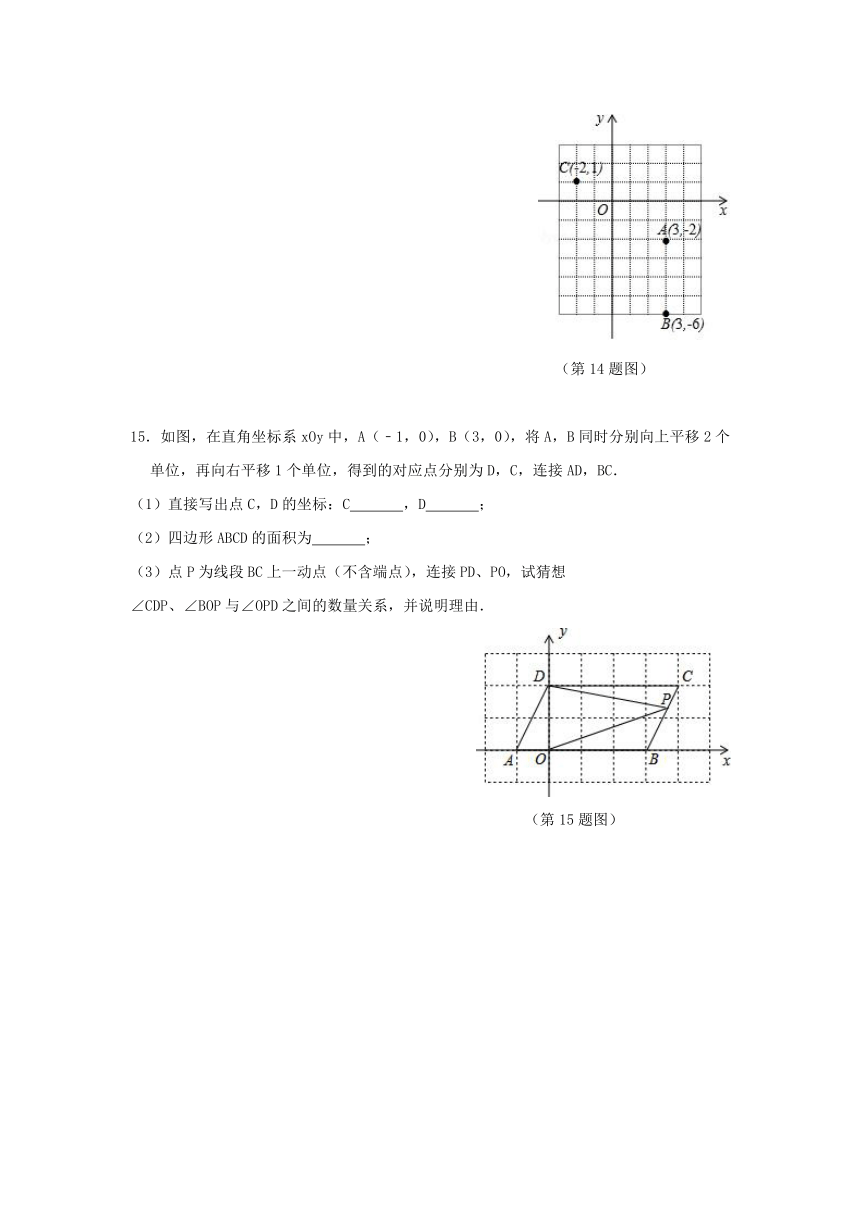
14.如图,在平面直角坐标系中有一个轴对称图形,A(3,﹣2),B(3,﹣6)两点在此图形上且互为对称点,若此图形上有一个点C(﹣2,+1).
(1)求点C的对称点的坐标.
(2)求△ABC的面积.
(第14题图)
15.如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.
(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD、PO,试猜想
∠CDP、∠BOP与∠OPD之间的数量关系,并说明理由.
(第15题图)
16.如图是学校的平面示意图,已知旗杆的位置是(﹣2,3),实验室的位置是(1,4).
(1)根据所给条件建立适当的平面直角坐标系,并用坐标表示食堂、图书馆的位置;
(2)已知办公楼的位置是(﹣2,1),教学楼的位置是(2,2),在图中标出办公楼和教学楼的位置;
(3)如果一个单位长度表示30米,请求出宿舍楼到教学楼的实际距离.
、
(第16题图)
17.在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)分别写出△ABC各个顶点的坐标;
(2)分别写出顶点A关于x轴对称的点A′的坐标、顶点B关于y轴对称的点B′的坐标及顶点C关于原点对称的点C′的坐标;
(3)求线段BC的长.
(第17题图)
18.已知:△ABC与△A'B'C在平面直角坐标系中的位置如图.
(1)分别写出B、B'的坐标:B ;B′ ;
(2)若点P(a,b)是△ABC内部一点,则平移后△A'B'C内的对应点P′的坐标为 ;
(3)求△ABC的面积.
(第18题图)
19.在平面直角坐标系中,已知点P(2m+4,m﹣1),试分别根据下列条件,求出点P的坐标.
求:(1)点P在y轴上;
(2)点P的纵坐标比横坐标大3;
(3)点P在过A(2,﹣5)点,且与x轴平行的直线上.
20.如图是一个平面直角坐标系.
(1)请在图中描出以下6个点:A(0,2)、B(4,2)、C(3,4)
A′(﹣4,﹣4)、B'(0,﹣4)、C′(﹣1,﹣2)
(2)分别顺次连接A、B、C和A′、B'、C',得到三角形ABC和三角形A′B′C′;
(3)观察所画的图形,判断三角形A′B′C′能否由三角形ABC平移得到,如果能,请说出三角形A′B′C′是由三角形ABC怎样平移得到的;如果不能,说明理由.
(第20题图)
参考答案
一.1.C【解析】∵正方形ABCD的边长为4,点A的坐标为(﹣1,1),AB平行于x轴,
∴点B的横坐标为﹣1+4=3,纵坐标为1.∴点B的坐标为(3,1).∴点C的横坐标为3,纵坐标为1+4=5.∴点C的坐标为(3,5).故选项A错误,选项B错误,选项C正确,选项D错误.故选C.
2.B【解析】∵点A(3﹣m,n+2)关于原点的对称点B的坐标是(﹣3,2),∴3﹣m=3,n+2=﹣2,m=0,n=﹣4.故选B.
3.D【解析】依题意有|x﹣2|+|y﹣1|=3,①x﹣2=±3,y﹣1=0,解得,;
②x﹣2=±2,y﹣1=±1,解得,,,;③x﹣2=±1,y﹣1=±2,解得,,,;④x﹣2=0,y﹣1=±3,解得,.故满足条件的点P有12个.故选D.
4.B【解析】如图所示.
由垂线段最短可知:当BC⊥AC时,BC有最小值.∴点C的坐标为(3,2),线段的最小值为2.故选B.
5.A【解析】各点的纵坐标都减去﹣3,也就是纵坐标加上3,上下移动改变点的纵坐标,下减,上加,而点的横坐标保持不变,故所得图形与原图形相比向上平移了3个单位.故选A.
6.B【解析】∵A(﹣3,0),B(0,4),∴OA=3,OB=4,∴AB==5,∴△ABC的周长=3+4+5=12.∵△OAB每连续3次后与原来的状态一样,2016=3×672,∴三角形2016与三角形1的状态一样,∴三角形2016的直角顶点的横坐标=672×12=8064,∴三角形2016的直角顶点坐标为(8064,0).∴△2016的直角顶点的横坐标为8064.故选B.
二.7.(36,0)【解析】由原图到图③,相当于向右平移了12个单位长度,象这样平移三次直角顶点是(36,0),再旋转一次到三角形⑩,直角顶点仍然是(36,0),则三角形⑩的直角顶点的坐标为(36,0).
8.(3,2)【解析】∵f(﹣3,2)=(﹣3,﹣2),∴g[f(﹣3,2)]=g(﹣3,﹣2)=(3,2).
9.(﹣5,4)【解析】如图,过点A作AC⊥y轴于点C,作AB⊥x轴于点B,过A′作A′E⊥y轴于点E,作A′D⊥x轴于点D.∵点A(4,5),∴AC=4,AB=5.∵点A(4,5)绕原点逆时针旋转90°得到点A′,∴A′E=AB=5,A′D=AC=4,∴点A′的坐标是(﹣5,4).
10.(m+2,n﹣1)【解析】由点A的平移规律可知,此题点的移动规律是(x+2,y﹣1),照此规律计算可知P’的坐标为(m+2,n﹣1).
11.(1,2)【解析】∵△ABO是关于x轴对称的轴对称图形,∴点A和点B的横坐标相同,纵坐标互为相反数,即点B的坐标为(1,2).
12.对应文字横坐标加1,纵坐标加2;“努力发挥”【解析】∵“正”所处的位置为(x,y),对应文字“祝”的位置是(x+1,y+2),∴找到的密码钥匙是对应文字横坐标加1,纵坐标加2,∴“今天考试”真实意思是“努力发挥”.
13.4【解析】分二种情况进行讨论:当OA为等腰三角形的腰时,以O为圆心OA为半径的圆弧与y轴有两个交点,以A为圆心AO为半径的圆弧与y轴有一个交点;当OA为等腰三角形的底时,作线段OA的垂直平分线,与y轴有一个交点.∴符合条件的点一共4个.
三.14.解:∵A、B关于某条直线对称,且A、B的横坐标相同,
∴对称轴平行于x轴.
又∵A的纵坐标为2,B的纵坐标为﹣6,
∴故对称轴为y==﹣2,
∴y=﹣2.
则设C(﹣2,1)关于y=﹣2的对称点为(﹣2,m),
于是=﹣2,
解得m=﹣5.
则C的对称点坐标为(﹣2,﹣5).
(2)如图所示,S△ABC=×(﹣2+6)×(3+2)=10.
(第14题答图)
15.解:(1)由图可知,C(4,2),D(0,2).
(2)∵线段CD由线段BA平移而成,
∴AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴S平行四边形ABCD=4×2=8.
(3)结论:∠CDP+∠BOP=∠OPD.
理由:如图,过点P作PQ∥AB,
∵CD∥AB,
∴CD∥PQ,AB∥PQ,
∴∠CDP=∠1,∠BOP=∠2,
∴∠CDP+∠BOP=∠1+∠2=∠OPD.
(第15题答图)
16.解:(1)如答图,食堂(﹣5,5)、图书馆的位置(2,5);
(2)如答图,办公楼和教学楼的位置即为所求;
(3)宿舍楼到教学楼的实际距离为8×30=240(m).
(第16题答图)
17.解:(1)A(﹣4,3),C(﹣2,5),B(3,0);
(2)如答图,点A′的坐标为:(﹣4,3),B′的坐标为:(﹣3,0),点C′的坐标为:(2,﹣5);
(3)线段BC的长为:=5.
(第17题答图)
18.解:(1)由图知,点B′的坐标为(2,0)、点B坐标为(﹣2,﹣2),
(2)由图知△ABC向左平移4个单位,再向下平移2个单位可得到△A'B'C′,
则平移后△A'B'C内的对应点P′的坐标为(a﹣4,b﹣2),
(3)△ABC的面积为2×3﹣×1×3﹣×1×1﹣×2×2=2.
19.解:(1)令2m+4=0,解得m=﹣2,所以P点的坐标为(0,﹣3);
(2)令m﹣1﹣(2m+4)=3,解得m=﹣8,所以P点的坐标为(﹣12,﹣9);
(3)令m﹣1=﹣5,解得m=﹣4.所以P点的坐标为(﹣4,﹣5).
20.解:(1)如答图.
(第20题答图)
(2)如图所示,△ABC和△A′B′C′即为所求;
(3)△A′B′C′是由△ABC向左平移4个单位,向下平移6个单位得到.
一.选择题
1.如图,正方形ABCD的边长为4,点A的坐标为(﹣1,1),AB平行于x轴,则点C的坐标为( )
(第1题图)
A.(3,1) B.(﹣1,1) C.(3,5) D.(﹣1,5)
2.若点A(3﹣m,n+2)关于原点的对称点B的坐标是(﹣3,2),则m,n的值为( )
A.m=﹣6,n=﹣4 B.m=0,n=﹣4 C.m=6,n=4 D.m=6,n=﹣4
3.P1(x1,y1),P2(x2,y2)是平面直角坐标系中的任意两点,我们把|x1﹣x2|+|y1﹣y2|叫做P1,P2两点间的“直角距离”,记作d(P1,P2).比如:点P(2,﹣4),Q(1,0),则d(P,Q)=|2﹣1|+|﹣4﹣0|=5,已知Q(2,1),动点P(x,y)满足d(P,Q)=3,且x、y均为整数,则满足条件的点P有( )个.
A.4 B.8 C.10 D.12
4.平面直角坐标系中,点A(﹣3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )
A.6,(﹣3,4) B.2,(3,2) C.2,(3,0) D.1,(4,2)
5.平面直角坐标系中,将三角形各点的纵坐标都减去﹣3,横坐标保持不变,所得图形与原图形相比( )
A.向上平移了3个单位 B.向下平移了3个单位
C.向右平移了3个单位 D.向左平移了3个单位
6.如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2016的直角顶点的横坐标为( )
(第6题图)
A.8065 B.8064 C.8063 D.8062
二.填空题
7.如图,在直角坐标系中,已知点A(﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到三角形①,②,③,④…,则三角形⑩的直角顶点的坐标为 .
(第7题图)
8.在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:
(1)f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);
(2)g(m,n)=(﹣m,﹣n),如g (2,1)=(﹣2,﹣1)
按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣3,2)]= .
9.在平面直角坐标系中,以原点为中心,把点A(4,5)逆时针旋转90°,得到的点A′的坐标为 .
10.如图,把图中的圆A经过平移得到圆O(如图),如果左图⊙A上一点P的坐标为(m,n),那么平移后在右图中的对应点P′的坐标为 .
(第10题图)
11.如图,△ABO是关于x轴对称的轴对称图形,点A的坐标为(1,﹣2),则点B的坐标为 .
(第11题图)
12.如图是一组密码的一部分,为了保密,许多情况下课采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“正做数学”的真实意思是“祝你成功”.若“正”所处的位置为(x,y),你找到的密码钥匙是 ,破译的“今天考试”真实意思是 .
(第12题图)
13.在平面直角坐标系xOy中,已知点A(2,﹣2),在y轴上确定点P,使△AOP为等腰三角形,则符合条件的有 个.
三.解答题
14.如图,在平面直角坐标系中有一个轴对称图形,A(3,﹣2),B(3,﹣6)两点在此图形上且互为对称点,若此图形上有一个点C(﹣2,+1).
(1)求点C的对称点的坐标.
(2)求△ABC的面积.
(第14题图)
15.如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.
(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD、PO,试猜想
∠CDP、∠BOP与∠OPD之间的数量关系,并说明理由.
(第15题图)
16.如图是学校的平面示意图,已知旗杆的位置是(﹣2,3),实验室的位置是(1,4).
(1)根据所给条件建立适当的平面直角坐标系,并用坐标表示食堂、图书馆的位置;
(2)已知办公楼的位置是(﹣2,1),教学楼的位置是(2,2),在图中标出办公楼和教学楼的位置;
(3)如果一个单位长度表示30米,请求出宿舍楼到教学楼的实际距离.
、
(第16题图)
17.在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)分别写出△ABC各个顶点的坐标;
(2)分别写出顶点A关于x轴对称的点A′的坐标、顶点B关于y轴对称的点B′的坐标及顶点C关于原点对称的点C′的坐标;
(3)求线段BC的长.
(第17题图)
18.已知:△ABC与△A'B'C在平面直角坐标系中的位置如图.
(1)分别写出B、B'的坐标:B ;B′ ;
(2)若点P(a,b)是△ABC内部一点,则平移后△A'B'C内的对应点P′的坐标为 ;
(3)求△ABC的面积.
(第18题图)
19.在平面直角坐标系中,已知点P(2m+4,m﹣1),试分别根据下列条件,求出点P的坐标.
求:(1)点P在y轴上;
(2)点P的纵坐标比横坐标大3;
(3)点P在过A(2,﹣5)点,且与x轴平行的直线上.
20.如图是一个平面直角坐标系.
(1)请在图中描出以下6个点:A(0,2)、B(4,2)、C(3,4)
A′(﹣4,﹣4)、B'(0,﹣4)、C′(﹣1,﹣2)
(2)分别顺次连接A、B、C和A′、B'、C',得到三角形ABC和三角形A′B′C′;
(3)观察所画的图形,判断三角形A′B′C′能否由三角形ABC平移得到,如果能,请说出三角形A′B′C′是由三角形ABC怎样平移得到的;如果不能,说明理由.
(第20题图)
参考答案
一.1.C【解析】∵正方形ABCD的边长为4,点A的坐标为(﹣1,1),AB平行于x轴,
∴点B的横坐标为﹣1+4=3,纵坐标为1.∴点B的坐标为(3,1).∴点C的横坐标为3,纵坐标为1+4=5.∴点C的坐标为(3,5).故选项A错误,选项B错误,选项C正确,选项D错误.故选C.
2.B【解析】∵点A(3﹣m,n+2)关于原点的对称点B的坐标是(﹣3,2),∴3﹣m=3,n+2=﹣2,m=0,n=﹣4.故选B.
3.D【解析】依题意有|x﹣2|+|y﹣1|=3,①x﹣2=±3,y﹣1=0,解得,;
②x﹣2=±2,y﹣1=±1,解得,,,;③x﹣2=±1,y﹣1=±2,解得,,,;④x﹣2=0,y﹣1=±3,解得,.故满足条件的点P有12个.故选D.
4.B【解析】如图所示.
由垂线段最短可知:当BC⊥AC时,BC有最小值.∴点C的坐标为(3,2),线段的最小值为2.故选B.
5.A【解析】各点的纵坐标都减去﹣3,也就是纵坐标加上3,上下移动改变点的纵坐标,下减,上加,而点的横坐标保持不变,故所得图形与原图形相比向上平移了3个单位.故选A.
6.B【解析】∵A(﹣3,0),B(0,4),∴OA=3,OB=4,∴AB==5,∴△ABC的周长=3+4+5=12.∵△OAB每连续3次后与原来的状态一样,2016=3×672,∴三角形2016与三角形1的状态一样,∴三角形2016的直角顶点的横坐标=672×12=8064,∴三角形2016的直角顶点坐标为(8064,0).∴△2016的直角顶点的横坐标为8064.故选B.
二.7.(36,0)【解析】由原图到图③,相当于向右平移了12个单位长度,象这样平移三次直角顶点是(36,0),再旋转一次到三角形⑩,直角顶点仍然是(36,0),则三角形⑩的直角顶点的坐标为(36,0).
8.(3,2)【解析】∵f(﹣3,2)=(﹣3,﹣2),∴g[f(﹣3,2)]=g(﹣3,﹣2)=(3,2).
9.(﹣5,4)【解析】如图,过点A作AC⊥y轴于点C,作AB⊥x轴于点B,过A′作A′E⊥y轴于点E,作A′D⊥x轴于点D.∵点A(4,5),∴AC=4,AB=5.∵点A(4,5)绕原点逆时针旋转90°得到点A′,∴A′E=AB=5,A′D=AC=4,∴点A′的坐标是(﹣5,4).
10.(m+2,n﹣1)【解析】由点A的平移规律可知,此题点的移动规律是(x+2,y﹣1),照此规律计算可知P’的坐标为(m+2,n﹣1).
11.(1,2)【解析】∵△ABO是关于x轴对称的轴对称图形,∴点A和点B的横坐标相同,纵坐标互为相反数,即点B的坐标为(1,2).
12.对应文字横坐标加1,纵坐标加2;“努力发挥”【解析】∵“正”所处的位置为(x,y),对应文字“祝”的位置是(x+1,y+2),∴找到的密码钥匙是对应文字横坐标加1,纵坐标加2,∴“今天考试”真实意思是“努力发挥”.
13.4【解析】分二种情况进行讨论:当OA为等腰三角形的腰时,以O为圆心OA为半径的圆弧与y轴有两个交点,以A为圆心AO为半径的圆弧与y轴有一个交点;当OA为等腰三角形的底时,作线段OA的垂直平分线,与y轴有一个交点.∴符合条件的点一共4个.
三.14.解:∵A、B关于某条直线对称,且A、B的横坐标相同,
∴对称轴平行于x轴.
又∵A的纵坐标为2,B的纵坐标为﹣6,
∴故对称轴为y==﹣2,
∴y=﹣2.
则设C(﹣2,1)关于y=﹣2的对称点为(﹣2,m),
于是=﹣2,
解得m=﹣5.
则C的对称点坐标为(﹣2,﹣5).
(2)如图所示,S△ABC=×(﹣2+6)×(3+2)=10.
(第14题答图)
15.解:(1)由图可知,C(4,2),D(0,2).
(2)∵线段CD由线段BA平移而成,
∴AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴S平行四边形ABCD=4×2=8.
(3)结论:∠CDP+∠BOP=∠OPD.
理由:如图,过点P作PQ∥AB,
∵CD∥AB,
∴CD∥PQ,AB∥PQ,
∴∠CDP=∠1,∠BOP=∠2,
∴∠CDP+∠BOP=∠1+∠2=∠OPD.
(第15题答图)
16.解:(1)如答图,食堂(﹣5,5)、图书馆的位置(2,5);
(2)如答图,办公楼和教学楼的位置即为所求;
(3)宿舍楼到教学楼的实际距离为8×30=240(m).
(第16题答图)
17.解:(1)A(﹣4,3),C(﹣2,5),B(3,0);
(2)如答图,点A′的坐标为:(﹣4,3),B′的坐标为:(﹣3,0),点C′的坐标为:(2,﹣5);
(3)线段BC的长为:=5.
(第17题答图)
18.解:(1)由图知,点B′的坐标为(2,0)、点B坐标为(﹣2,﹣2),
(2)由图知△ABC向左平移4个单位,再向下平移2个单位可得到△A'B'C′,
则平移后△A'B'C内的对应点P′的坐标为(a﹣4,b﹣2),
(3)△ABC的面积为2×3﹣×1×3﹣×1×1﹣×2×2=2.
19.解:(1)令2m+4=0,解得m=﹣2,所以P点的坐标为(0,﹣3);
(2)令m﹣1﹣(2m+4)=3,解得m=﹣8,所以P点的坐标为(﹣12,﹣9);
(3)令m﹣1=﹣5,解得m=﹣4.所以P点的坐标为(﹣4,﹣5).
20.解:(1)如答图.
(第20题答图)
(2)如图所示,△ABC和△A′B′C′即为所求;
(3)△A′B′C′是由△ABC向左平移4个单位,向下平移6个单位得到.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
