湘教版八年级下册数学第一章《直角三角形》同步检测含答案
文档属性
| 名称 | 湘教版八年级下册数学第一章《直角三角形》同步检测含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 79.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-03 00:00:00 | ||
图片预览


文档简介
直角三角形
一、填空题
1、如图,为测得池塘两岸点A和点B间的距离,一个观测者在C点设桩,使∠ABC=90°,并测得AC长50m,BC长40m,则A、B两点间的距离是 。
2、将一根长为15cm的筷子置于底面直径为5cm,高12cm的圆柱形水杯中,设筷子露在杯子外面的长度为h cm,则h的取值范围是 。
3、在△ABC中,AB=AC,BD⊥AC于D,若BD=3,DC=1,则AD= 。
4、如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=1,则EF= .
5、如图,点M、A、N在一条直线上,△ABC为等腰三角形,AB=AC,BM⊥MN,CN⊥MN,垂足分别是M、N,且BM=AN,则MN与BM、CN之间的数量关系是 。
6、如图,已知△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,CE和BD交于点O,AO的延长线交BC于点F,则图中全等三角形的对数是 。
7、如图,△ABC的三边AB、BC、CA的长分别是12、10、6,其三条角平分线的交点为O,则S△ABO ︰S△BCO ︰S△CAO= .
8、如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于 。
9.到一个角的两边距离相等的点都在_________.
10.∠AOB的平分线上一点M ,M到 OA的距离为1.5 cm,则M到OB的距离为_______.
11.如图1,∠AOB=60°,CD⊥OA于D,CE⊥OB于E,且CD=CE,则∠DOC=____.
图1 图2
12.如图2,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于E,且DE=3 cm,BD=5 cm,则BC=_________ cm.
13.如图3,已知AB、CD相交于点E,过E作∠AEC及∠AED的平分线PQ与MN,则直线MN与PQ的关系是_________.
二、选择题
1.下列各语句中,不是真命题的是( )
A.直角都相等
B.等角的补角相等
C.点P在角的平分线上
D.对顶角相等
2.下列命题中是真命题的是( )
A.有两角及其中一角的平分线对应相等的两个三角形全等
B.相等的角是对顶角
C.余角相等的角互余
D.两直线被第三条直线所截,截得的同位角相等
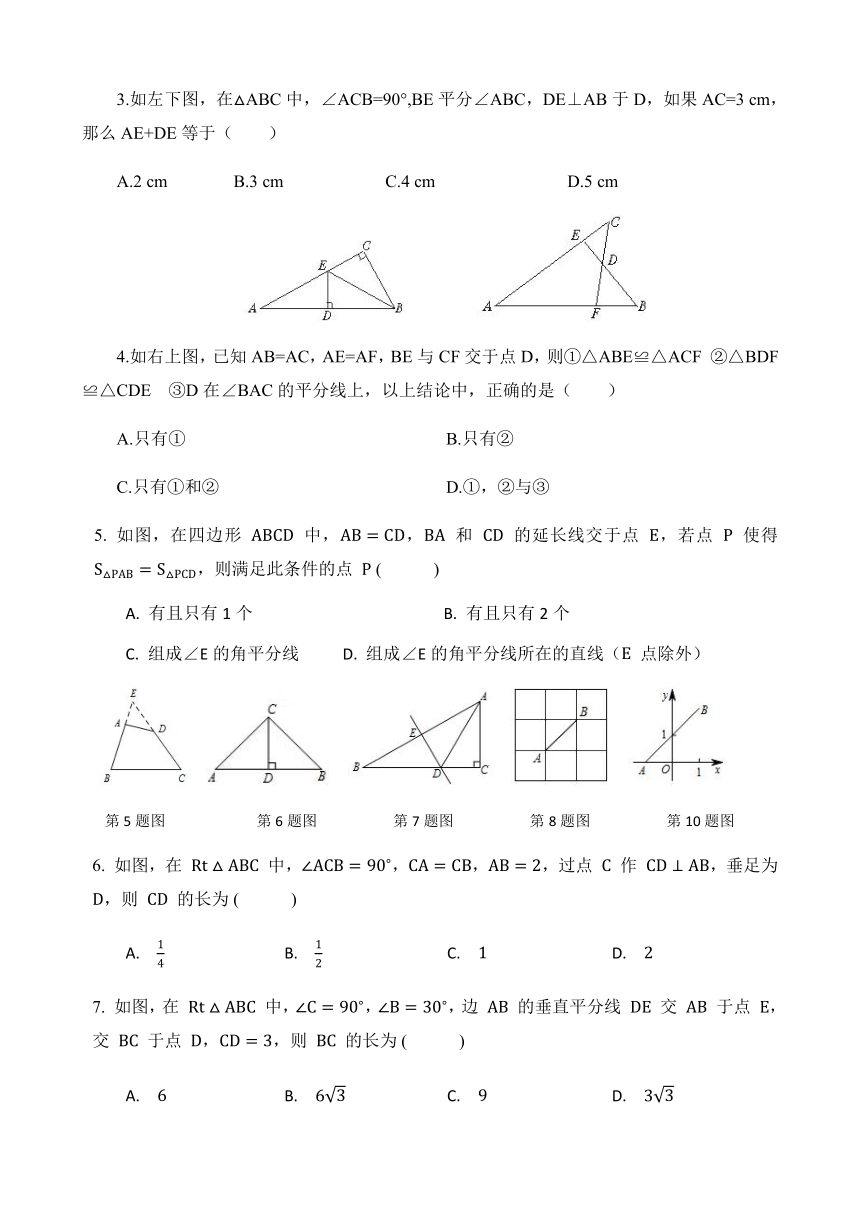
3.如左下图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3 cm,那么AE+DE等于( )
A.2 cm B.3 cm C.4 cm D.5 cm
4.如右上图,已知AB=AC,AE=AF,BE与CF交于点D,则①△ABE≌△ACF ②△BDF≌△CDE ③D在∠BAC的平分线上,以上结论中,正确的是( )
A.只有① B.只有②
C.只有①和② D.①,②与③
5. 如图,在四边形 中,, 和 的延长线交于点 ,若点 使得 ,则满足此条件的点 ?( )
A. 有且只有1个 B. 有且只有2个
C. 组成∠E的角平分线 D. 组成∠E的角平分线所在的直线( 点除外)
第5题图 第6题图 第7题图 第8题图 第10题图
6. 如图,在 中,,,,过点 作 ,垂足为 ,则 的长为?( )
A. B. C. D.
7. 如图,在 中,,,边 的垂直平分线 交 于点 ,交 于点 ,,则 的长为?( )
A. B. C. D.
8. 如图所示的正方形网格中,网格线的交点称为格点.已知 , 是两格点,如果 也是图中的格点,且使得 为等腰三角形,则点 的个数是?( )
A. B. C. D.
9. 下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
10. 如图,已知点 和点 ,在坐标轴上确定点 ,使得 为直角三角形,则满足这样条件的点 共有?( )
A. 个 B. 个 C. 个 D. 个
三、解答题
1.如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
求证:△ADE≌△BEC.
2.如图,AD是△ABC的高,E为AC上一点,BE交AD于点F,若有BF=AC,FD=CD,试探究BE与AC的位置关系.
3.用尺规作一个直角三角形,使其中一条边长为a,这条边所对的角为30°.
4、“交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h,如图,一辆小汽车在一条城街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A点正前方30m处的C点,过了2s后,测得小汽车与车速检测仪间的距离为50m,这辆小汽车超速了吗?
5、如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,E、F是垂足,AE=AF,求证:(1)PE=PF;(2)点P在∠BAC的角平分线上;
参考答案
一、1、30;2、;3、4;4、2;5、MN=BM+CN;
6、7对;7、6︰5︰3;8、6;
10.这个角的平分线上 11.1.5cm 3.30° 12.8 13.MN⊥PQ
二、1.C 2.A 3.B 4. D 5.D 6.C 7.C 8.C 9.C 10.C
三、1.证明:∵∠1=∠2,∴DE=CE.
∵AD∥BC,∠A=90°,
∴∠B=90°.
∴△ADE和△EBC是直角三角形.
而AD=BE,DE=CE,
∴△ADE≌△BEC(HL).
2.BE与AC垂直.
理由:∵AD是△ABC的高,
∴∠BDF=∠ADC=90°.
∴在Rt△BDF和Rt△ADC中,BF=AC,FD=CD.
∴Rt△BDF≌△Rt△ADC(HL).
∴∠DBF=∠DAC.
∵∠ADC=90°,
∴∠DAC+∠ACD=90°.
∴∠DBF+∠ACD=90°.
∴∠BEC=90°.
∴BE⊥AC.
3.已知:线段a,
求作:Rt△ABC,使BC=a,∠ACB=90°,∠A=30°.
作法:(1)作∠MCN=90°.
(2)在CN上截取CB,使CB=a.
(3)以B为圆心,以2a为半径画弧,交CM于点A,连接AB.
则△ABC为所求作的直角三角形.
4、由题意知AC=30m,AB=50m,∵AC⊥BC,
∴,∴BC=40m,
∴,这辆小汽车超速了。
5、证明:(1)连接AP并延长,∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=90°,又∵AE=AF,AP=AP;
∴Rt△AEP≌Rt△AFP(HL);∴PE=PF;
(2)∵Rt△AEP≌Rt△AFP(HL);∴∠EAP=∠FAP,
∴AP是∠BAC的角平分线;即:点P在∠BAC的角平分线上;
一、填空题
1、如图,为测得池塘两岸点A和点B间的距离,一个观测者在C点设桩,使∠ABC=90°,并测得AC长50m,BC长40m,则A、B两点间的距离是 。
2、将一根长为15cm的筷子置于底面直径为5cm,高12cm的圆柱形水杯中,设筷子露在杯子外面的长度为h cm,则h的取值范围是 。
3、在△ABC中,AB=AC,BD⊥AC于D,若BD=3,DC=1,则AD= 。
4、如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=1,则EF= .
5、如图,点M、A、N在一条直线上,△ABC为等腰三角形,AB=AC,BM⊥MN,CN⊥MN,垂足分别是M、N,且BM=AN,则MN与BM、CN之间的数量关系是 。
6、如图,已知△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,CE和BD交于点O,AO的延长线交BC于点F,则图中全等三角形的对数是 。
7、如图,△ABC的三边AB、BC、CA的长分别是12、10、6,其三条角平分线的交点为O,则S△ABO ︰S△BCO ︰S△CAO= .
8、如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于 。
9.到一个角的两边距离相等的点都在_________.
10.∠AOB的平分线上一点M ,M到 OA的距离为1.5 cm,则M到OB的距离为_______.
11.如图1,∠AOB=60°,CD⊥OA于D,CE⊥OB于E,且CD=CE,则∠DOC=____.
图1 图2
12.如图2,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于E,且DE=3 cm,BD=5 cm,则BC=_________ cm.
13.如图3,已知AB、CD相交于点E,过E作∠AEC及∠AED的平分线PQ与MN,则直线MN与PQ的关系是_________.
二、选择题
1.下列各语句中,不是真命题的是( )
A.直角都相等
B.等角的补角相等
C.点P在角的平分线上
D.对顶角相等
2.下列命题中是真命题的是( )
A.有两角及其中一角的平分线对应相等的两个三角形全等
B.相等的角是对顶角
C.余角相等的角互余
D.两直线被第三条直线所截,截得的同位角相等
3.如左下图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3 cm,那么AE+DE等于( )
A.2 cm B.3 cm C.4 cm D.5 cm
4.如右上图,已知AB=AC,AE=AF,BE与CF交于点D,则①△ABE≌△ACF ②△BDF≌△CDE ③D在∠BAC的平分线上,以上结论中,正确的是( )
A.只有① B.只有②
C.只有①和② D.①,②与③
5. 如图,在四边形 中,, 和 的延长线交于点 ,若点 使得 ,则满足此条件的点 ?( )
A. 有且只有1个 B. 有且只有2个
C. 组成∠E的角平分线 D. 组成∠E的角平分线所在的直线( 点除外)
第5题图 第6题图 第7题图 第8题图 第10题图
6. 如图,在 中,,,,过点 作 ,垂足为 ,则 的长为?( )
A. B. C. D.
7. 如图,在 中,,,边 的垂直平分线 交 于点 ,交 于点 ,,则 的长为?( )
A. B. C. D.
8. 如图所示的正方形网格中,网格线的交点称为格点.已知 , 是两格点,如果 也是图中的格点,且使得 为等腰三角形,则点 的个数是?( )
A. B. C. D.
9. 下列每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
10. 如图,已知点 和点 ,在坐标轴上确定点 ,使得 为直角三角形,则满足这样条件的点 共有?( )
A. 个 B. 个 C. 个 D. 个
三、解答题
1.如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
求证:△ADE≌△BEC.
2.如图,AD是△ABC的高,E为AC上一点,BE交AD于点F,若有BF=AC,FD=CD,试探究BE与AC的位置关系.
3.用尺规作一个直角三角形,使其中一条边长为a,这条边所对的角为30°.
4、“交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h,如图,一辆小汽车在一条城街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A点正前方30m处的C点,过了2s后,测得小汽车与车速检测仪间的距离为50m,这辆小汽车超速了吗?
5、如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,E、F是垂足,AE=AF,求证:(1)PE=PF;(2)点P在∠BAC的角平分线上;
参考答案
一、1、30;2、;3、4;4、2;5、MN=BM+CN;
6、7对;7、6︰5︰3;8、6;
10.这个角的平分线上 11.1.5cm 3.30° 12.8 13.MN⊥PQ
二、1.C 2.A 3.B 4. D 5.D 6.C 7.C 8.C 9.C 10.C
三、1.证明:∵∠1=∠2,∴DE=CE.
∵AD∥BC,∠A=90°,
∴∠B=90°.
∴△ADE和△EBC是直角三角形.
而AD=BE,DE=CE,
∴△ADE≌△BEC(HL).
2.BE与AC垂直.
理由:∵AD是△ABC的高,
∴∠BDF=∠ADC=90°.
∴在Rt△BDF和Rt△ADC中,BF=AC,FD=CD.
∴Rt△BDF≌△Rt△ADC(HL).
∴∠DBF=∠DAC.
∵∠ADC=90°,
∴∠DAC+∠ACD=90°.
∴∠DBF+∠ACD=90°.
∴∠BEC=90°.
∴BE⊥AC.
3.已知:线段a,
求作:Rt△ABC,使BC=a,∠ACB=90°,∠A=30°.
作法:(1)作∠MCN=90°.
(2)在CN上截取CB,使CB=a.
(3)以B为圆心,以2a为半径画弧,交CM于点A,连接AB.
则△ABC为所求作的直角三角形.
4、由题意知AC=30m,AB=50m,∵AC⊥BC,
∴,∴BC=40m,
∴,这辆小汽车超速了。
5、证明:(1)连接AP并延长,∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=90°,又∵AE=AF,AP=AP;
∴Rt△AEP≌Rt△AFP(HL);∴PE=PF;
(2)∵Rt△AEP≌Rt△AFP(HL);∴∠EAP=∠FAP,
∴AP是∠BAC的角平分线;即:点P在∠BAC的角平分线上;
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
