8.4.4 分组分解法(要点测评+课后集训+答案)
文档属性
| 名称 | 8.4.4 分组分解法(要点测评+课后集训+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-04 00:00:00 | ||
图片预览

文档简介
沪科版数学七年级下册同步课时训练
第8章 整式乘法与因式分解
8.4 因式分解
2.公式法
第3课时 分组分解法
要点测评 基础达标
要点1 分组分解法
1. 若x2-y2-x+y=(x-y)·A,则A= .?
2. 分解因式:
(1)x2-y2+ax+ay;
(2)c2-a2-2ab-b2.
要点2 x2+(p+q)x+pq型二次三项式的因式分解
3. 多项式ax2-4ax-12a因式分解正确的是( )
A. a(x-6)(x+2) B. a(x-3)(x+4)
C. a(x2-4x-12) D. a(x+6)(x-2)
4. 分解因式:
(1)x2-3x+2;
(2)x2+3x+2.
要点3 因式分解的综合应用
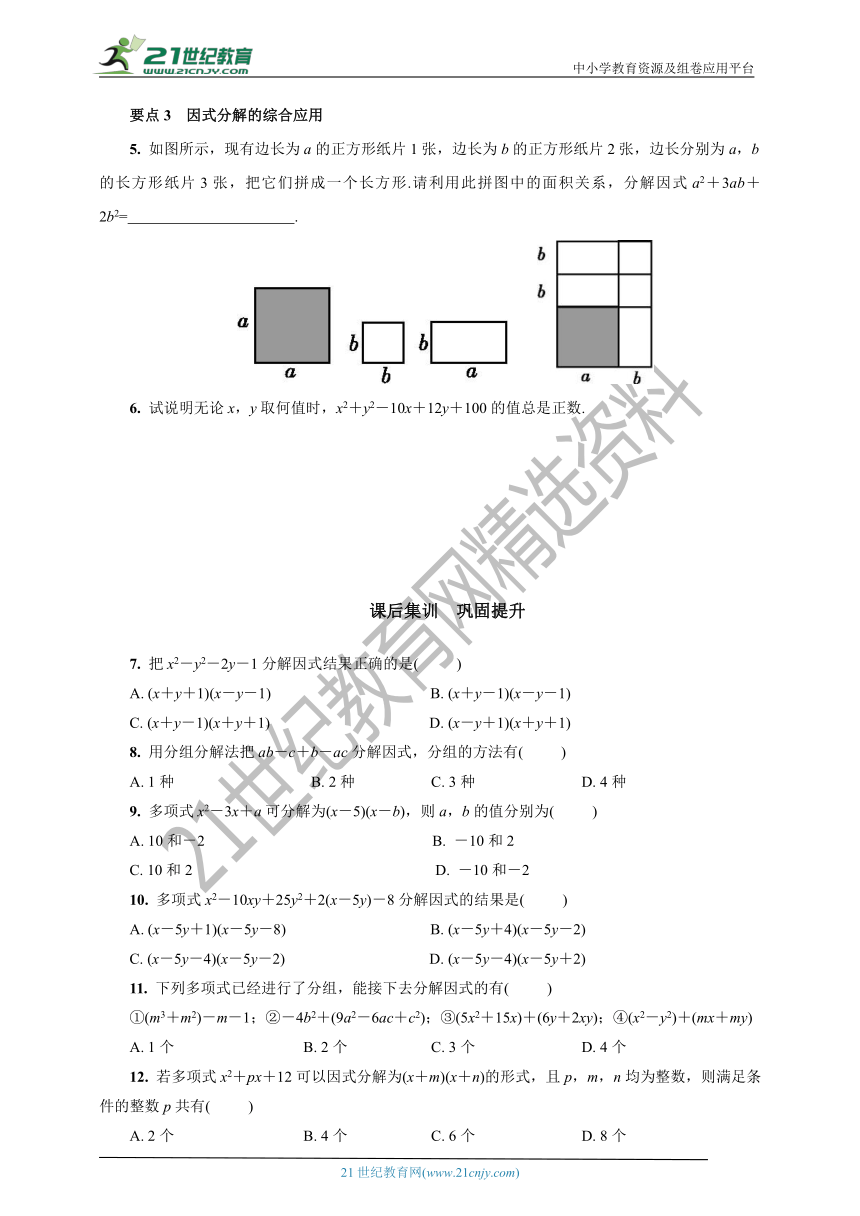
5. 如图所示,现有边长为a的正方形纸片1张,边长为b的正方形纸片2张,边长分别为a,b的长方形纸片3张,把它们拼成一个长方形.请利用此拼图中的面积关系,分解因式a2+3ab+2b2= .
6. 试说明无论x,y取何值时,x2+y2-10x+12y+100的值总是正数.
课后集训 巩固提升
7. 把x2-y2-2y-1分解因式结果正确的是( )
A. (x+y+1)(x-y-1) B. (x+y-1)(x-y-1)
C. (x+y-1)(x+y+1) D. (x-y+1)(x+y+1)
8. 用分组分解法把ab-c+b-ac分解因式,分组的方法有( )
A. 1种 B. 2种 C. 3种 D. 4种
9. 多项式x2-3x+a可分解为(x-5)(x-b),则a,b的值分别为( )
A. 10和-2 B. -10和2
C. 10和2 D. -10和-2
10. 多项式x2-10xy+25y2+2(x-5y)-8分解因式的结果是( )
A. (x-5y+1)(x-5y-8) B. (x-5y+4)(x-5y-2)
C. (x-5y-4)(x-5y-2) D. (x-5y-4)(x-5y+2)
11. 下列多项式已经进行了分组,能接下去分解因式的有( )
①(m3+m2)-m-1;②-4b2+(9a2-6ac+c2);③(5x2+15x)+(6y+2xy);④(x2-y2)+(mx+my)
A. 1个 B. 2个 C. 3个 D. 4个
12. 若多项式x2+px+12可以因式分解为(x+m)(x+n)的形式,且p,m,n均为整数,则满足条件的整数p共有( )
A. 2个 B. 4个 C. 6个 D. 8个
13. 分解因式:(x+2)(x+4)+x2-4= .?
14. 分解因式:(x2+x+1)(x2+x+2)-12= .?
15. 已知2a+b+c=6,2a+b-c=4,则4a2+4ab+b2-c2= .?
16. 甲、乙两个同学分解因式x2+ax+b时,甲看错了b,分解结果为(x+2)(x+4);乙看错了a,分解结果为(x+1)(x+9),则a= ,b= .?
17. 分解因式:
(1)x3+x2y-xy2-y3; (2)a2-4b2+12bc-9c2;
(3)2x2-5x-3; (4)x4-10x2+9.
18. 已知x2-2xy-3y2=5,求整数x和y的值.
参 考 答 案
1. x+y-1
2. 解:(1)x2-y2+ax+ay=(x2-y2)+(ax+ay)=(x+y)(x-y)+a(x+y)=(x+y)[(x-y)+a]=(x+y)(x-y+a).
(2)c2-a2-2ab-b2=c2-(a2+2ab+b2)=c2-(a+b)2=(c+a+b)(c-a-b).
3. A
4. 解:(1)x2-3x+2=(x-2)(x-1).
(2)x2+3x+2=(x+1)(x+2).
5. (a+b)(a+2b)
6. 解:x2+y2-10x+12y+100=(x2-10x+25)+(y2+12y+36)+39=(x-5)2+(y+6)2+39,因为(x-5)2≥0,(y+6)2≥0,所以(x-5)2+(y+6)2+39≥39. 所以无论x,y取何值时,x2+y2-10x+12y+100的值总是正数.
7. A
8. B
9. D
10. B
11. D
12. C
13. 2(x+2)(x+1)
14. (x2+x+5)(x+2)(x-1)
15. 24
16. 6 9
17. 解:(1)x3+x2y-xy2-y3=(x3+x2y)-(xy2+y3)=x2(x+y)-y2(x+y)=(x+y)(x2-y2)=(x+y)(x+y)(x-y)=(x+y)2(x-y).
(2)a2-4b2+12bc-9c2=a2-(4b2-12bc+9c2)=a2-(2b-3c)2=[a+(2b-3c)][a-(2b-3c)]=(a+2b-3c)(a-2b+3c).
(3)2x2-5x-3=(2x+1)(x-3).
(4)x4-10x2+9=(x2-1)(x2-9)=(x+1)(x-1)(x+3)(x-3).
18. 解:因为x2-2xy-3y2=5,所以(x-3y)(x+y)=5. 依题意 x,y为整数,所以 x-3y和 x+y都是整数,于是有或或或 解上述方程组得或或或
第8章 整式乘法与因式分解
8.4 因式分解
2.公式法
第3课时 分组分解法
要点测评 基础达标
要点1 分组分解法
1. 若x2-y2-x+y=(x-y)·A,则A= .?
2. 分解因式:
(1)x2-y2+ax+ay;
(2)c2-a2-2ab-b2.
要点2 x2+(p+q)x+pq型二次三项式的因式分解
3. 多项式ax2-4ax-12a因式分解正确的是( )
A. a(x-6)(x+2) B. a(x-3)(x+4)
C. a(x2-4x-12) D. a(x+6)(x-2)
4. 分解因式:
(1)x2-3x+2;
(2)x2+3x+2.
要点3 因式分解的综合应用
5. 如图所示,现有边长为a的正方形纸片1张,边长为b的正方形纸片2张,边长分别为a,b的长方形纸片3张,把它们拼成一个长方形.请利用此拼图中的面积关系,分解因式a2+3ab+2b2= .
6. 试说明无论x,y取何值时,x2+y2-10x+12y+100的值总是正数.
课后集训 巩固提升
7. 把x2-y2-2y-1分解因式结果正确的是( )
A. (x+y+1)(x-y-1) B. (x+y-1)(x-y-1)
C. (x+y-1)(x+y+1) D. (x-y+1)(x+y+1)
8. 用分组分解法把ab-c+b-ac分解因式,分组的方法有( )
A. 1种 B. 2种 C. 3种 D. 4种
9. 多项式x2-3x+a可分解为(x-5)(x-b),则a,b的值分别为( )
A. 10和-2 B. -10和2
C. 10和2 D. -10和-2
10. 多项式x2-10xy+25y2+2(x-5y)-8分解因式的结果是( )
A. (x-5y+1)(x-5y-8) B. (x-5y+4)(x-5y-2)
C. (x-5y-4)(x-5y-2) D. (x-5y-4)(x-5y+2)
11. 下列多项式已经进行了分组,能接下去分解因式的有( )
①(m3+m2)-m-1;②-4b2+(9a2-6ac+c2);③(5x2+15x)+(6y+2xy);④(x2-y2)+(mx+my)
A. 1个 B. 2个 C. 3个 D. 4个
12. 若多项式x2+px+12可以因式分解为(x+m)(x+n)的形式,且p,m,n均为整数,则满足条件的整数p共有( )
A. 2个 B. 4个 C. 6个 D. 8个
13. 分解因式:(x+2)(x+4)+x2-4= .?
14. 分解因式:(x2+x+1)(x2+x+2)-12= .?
15. 已知2a+b+c=6,2a+b-c=4,则4a2+4ab+b2-c2= .?
16. 甲、乙两个同学分解因式x2+ax+b时,甲看错了b,分解结果为(x+2)(x+4);乙看错了a,分解结果为(x+1)(x+9),则a= ,b= .?
17. 分解因式:
(1)x3+x2y-xy2-y3; (2)a2-4b2+12bc-9c2;
(3)2x2-5x-3; (4)x4-10x2+9.
18. 已知x2-2xy-3y2=5,求整数x和y的值.
参 考 答 案
1. x+y-1
2. 解:(1)x2-y2+ax+ay=(x2-y2)+(ax+ay)=(x+y)(x-y)+a(x+y)=(x+y)[(x-y)+a]=(x+y)(x-y+a).
(2)c2-a2-2ab-b2=c2-(a2+2ab+b2)=c2-(a+b)2=(c+a+b)(c-a-b).
3. A
4. 解:(1)x2-3x+2=(x-2)(x-1).
(2)x2+3x+2=(x+1)(x+2).
5. (a+b)(a+2b)
6. 解:x2+y2-10x+12y+100=(x2-10x+25)+(y2+12y+36)+39=(x-5)2+(y+6)2+39,因为(x-5)2≥0,(y+6)2≥0,所以(x-5)2+(y+6)2+39≥39. 所以无论x,y取何值时,x2+y2-10x+12y+100的值总是正数.
7. A
8. B
9. D
10. B
11. D
12. C
13. 2(x+2)(x+1)
14. (x2+x+5)(x+2)(x-1)
15. 24
16. 6 9
17. 解:(1)x3+x2y-xy2-y3=(x3+x2y)-(xy2+y3)=x2(x+y)-y2(x+y)=(x+y)(x2-y2)=(x+y)(x+y)(x-y)=(x+y)2(x-y).
(2)a2-4b2+12bc-9c2=a2-(4b2-12bc+9c2)=a2-(2b-3c)2=[a+(2b-3c)][a-(2b-3c)]=(a+2b-3c)(a-2b+3c).
(3)2x2-5x-3=(2x+1)(x-3).
(4)x4-10x2+9=(x2-1)(x2-9)=(x+1)(x-1)(x+3)(x-3).
18. 解:因为x2-2xy-3y2=5,所以(x-3y)(x+y)=5. 依题意 x,y为整数,所以 x-3y和 x+y都是整数,于是有或或或 解上述方程组得或或或
