苏教版高中数学必修一教学讲义,复习补习资料(含典例分析,巩固练习):20分数指数幂(提高)
文档属性
| 名称 | 苏教版高中数学必修一教学讲义,复习补习资料(含典例分析,巩固练习):20分数指数幂(提高) |

|
|
| 格式 | zip | ||
| 文件大小 | 222.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 00:00:00 | ||
图片预览

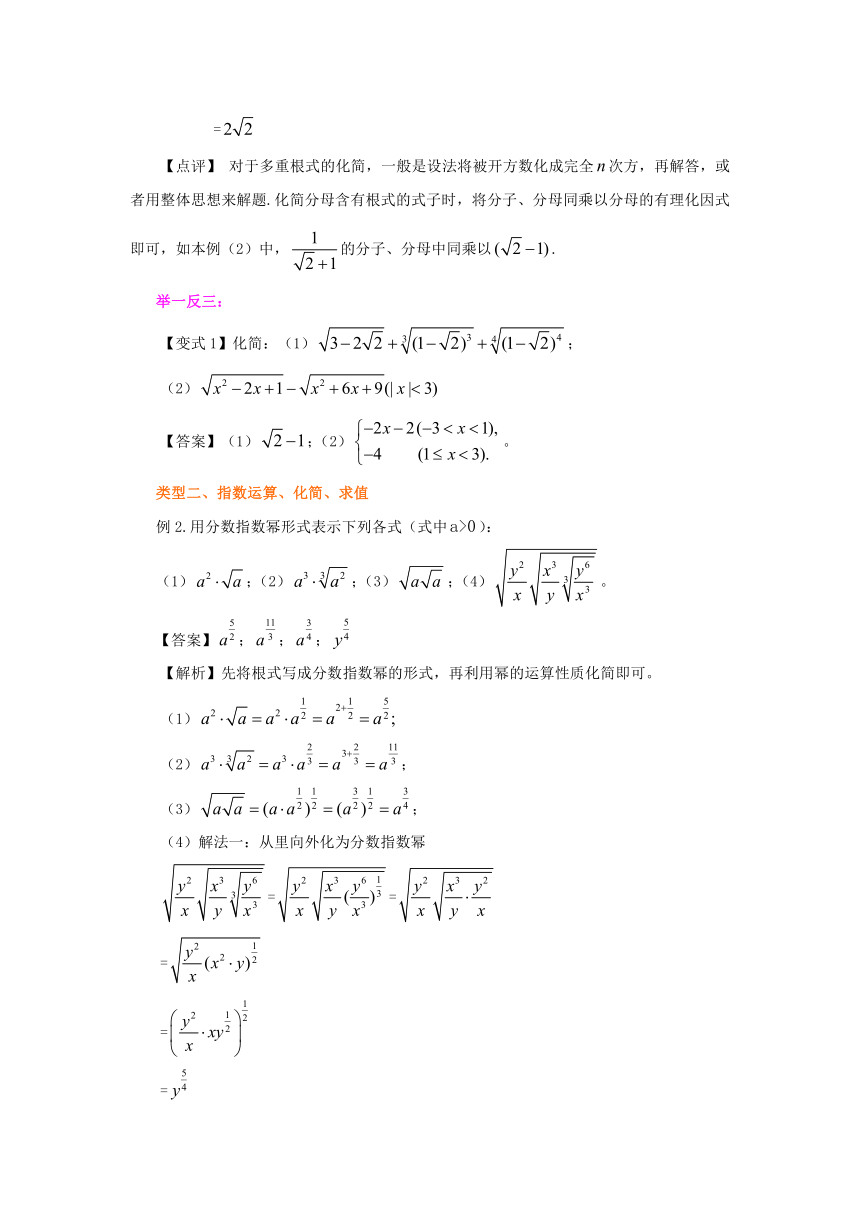



文档简介
分数指数幂
【学习目标】
理解分数指数的含义,了解实数指数幂的意义,理解n次方根,n次根式的概念,熟练掌握用根式与分数指数幂表示一个正实数的算术根;能运用有理指数幂的运算性质进行运算和化简,会进行根式与分数指数幂的相互转化。
【典型例题】
类型一、根式
例1.计算:(1);
(2).
【答案】
【解析】对于(1)需把各项被开方数变为完全平方形式,然后再利用根式运算性质求解.对于(2),则应分子、分母同乘以分母的有理化因式.
(1)
=+-
=
=||+||-||
=+-()
=2
(2)
=
=
=
【点评】 对于多重根式的化简,一般是设法将被开方数化成完全次方,再解答,或者用整体思想来解题.化简分母含有根式的式子时,将分子、分母同乘以分母的有理化因式即可,如本例(2)中,的分子、分母中同乘以.
举一反三:
【变式1】化简:(1);
(2)
【答案】(1);(2)。
类型二、指数运算、化简、求值
例2.用分数指数幂形式表示下列各式(式中):
(1);(2);(3);(4)。
【答案】;;;
【解析】先将根式写成分数指数幂的形式,再利用幂的运算性质化简即可。
(1)
(2);
(3);
(4)解法一:从里向外化为分数指数幂
==
=
=
=
解法二:从外向里化为分数指数幂。
=
==
=
=
【点评】此类问题应熟练应用。当所求根式含有多重根号时,要搞清被开方数,由里向外或由外向里,用分数指数幂写出,然后再用性质进行化简。
举一反三:
【变式1】把下列根式用指数形式表示出来,并化简
(1);
【答案】(1);(2)。
【变式2】把下列根式化成分数指数幂:
(1);(2);(3);(4)。
【答案】;;;
【解析】(1)=;
(2);
(3);
(4)=
=。
例3.计算:
(1);
(2)
(3)。
【答案】3;0;2
【解析】(1)原式=;
(2)原式=;
(3)原式=-5+6+4--(3-)=2;
【点评】(1)运算顺序(能否应用公式);(2)指数为负先化正;(3)根式化为分数指数幂.
举一反三:
【变式1】计算下列各式:
(1); (2).
【答案】(1)112 (2)
【解析】(1)原式=;
(2)原式.
例4.化简下列各式.
(1) ; (2); (3).
【答案】;;0.09
【解析】(1)即合并同类项的想法,常数与常数进行运算,同一字母的化为该字母的指数运算;(2)对字母运算的理解要求较高,即能够认出分数指数的完全平方关系;(3)具体数字的运算,学会如何简化运算.
(1)
(2)
(3)
举一反三:
【变式1】化简
【答案】
【解析】应注意到之间的关系,对分子使用乘法公式进行因式分解,
原式
.
【点评】根式的化简结果应写为最简根式.(1)被开方数的指数与根指数互质;(2)被开方数分母为1,且不含非正整数指数幂;(3)被开方数的每个因数的指数小于根指数.
【变式2】化简下列式子:
(1) (2) (3)
【答案】;;
【解析】(1)原式
(2)
∴由平方根的定义得:
(3)
.
例5.已知,求的值。
【答案】
【解析】从已知条件中解出的值,然后代入求值,这种方法是不可取的,而应设法从整体寻求结果与条件的联系,进而整体代入求值。
,,
,
=
=
【点评】对于“条件求值”问题一定要弄清已知与未知的联系,然后采用“整体代换”或“化简后代换”方法求值。本题的关键是先求及的值,然后整体代入。
举一反三:
【变式1】(1)已知2x+2-x=a(a为常数),求8x+8-x的值.
(2)已知x+y=12, xy=9,且x【答案】;
【解析】(1)8x+8-x=23x+2-3x=(2x)3+(2-x)3
(2)
又∵ x+y=12, xy=9, ∴(x-y)2=(x+y)2-4xy=122-4×9=108.
又 ∵ x【点评】(1)对幂值的计算,一般应尽可能把幂化为底数是质数的指数幂,再考虑同底幂的运算法则以及乘法公式.
(2)一般不采用分别把x, y, 2x的值求出来代入求值的方法,应先将原式进行分母有理化,并用乘法公式变形,把2x+2-x,x+y及xy整体代入后再求值.
例6.已知,求的值
【答案】
【解析】先把化成,然后利用“整体代换”的方法去求值.
由,所以
=
例7. 已知a=,b=9.求:
(1)
(2).
【解析】(1)原式=.÷[a·]?
= =a.?
∵a=,∴原式=3.?
(2)方法一 化去负指数后解.?
∵a=∴a+b=
方法二 利用运算性质解.?
∵a=∴a+b=
【巩固练习】
1.化简,结果是( )
A. B. C. D.
2. 计算的结果是( )
A.32 B.16 C. 64 D.128
3.若,且,则的值等于( )
A. B. C. D.2
4.下列各式中错误的是( )
A.
B.
C.
D.
5.、、这三个数的大小关系为( )
A. B. C. D.
6. 已知定义在上的奇函数和偶函数满足
,若,则( )
A. 2 B. C. D.
7. .
8.= .
9.若,则= .
10.已知,则= .
11.计算:
(1);
(2).
12.计算下列各式:
(1);
(2).
13. 计算: 14.已知.
求证:为定值.
15.(1)化简:;
(2)已知,求的值.
【答案与解析】
1. A 原式=
=
=
=
2. A ,故选A。
3. C 因为,所以,即.同理,又因为,所以,故.
4.D D中左边=
5. B ,,.,.
6.B 因为,又是奇函数,是偶函数,所以,所以,,两式联立解得,进一步求得.
7. 原式=.
8. 原式=.
9.-23 原式===4-27=-23.
10. 因为,所以.
11.解:(1)原式=.
(2)原式=
=
=
=
=
12.解:(1)原式=
=
=.
(2)原式=
=-()
=0
13. 原式=
=
=
=0
14.证明:
同理
原式=2,结论得证.
15.解:(1)原式==+
=
(2)因为,
所以 ,
所以
故当 a>b时, =a-b.当a=b时,=0.当a
【学习目标】
理解分数指数的含义,了解实数指数幂的意义,理解n次方根,n次根式的概念,熟练掌握用根式与分数指数幂表示一个正实数的算术根;能运用有理指数幂的运算性质进行运算和化简,会进行根式与分数指数幂的相互转化。
【典型例题】
类型一、根式
例1.计算:(1);
(2).
【答案】
【解析】对于(1)需把各项被开方数变为完全平方形式,然后再利用根式运算性质求解.对于(2),则应分子、分母同乘以分母的有理化因式.
(1)
=+-
=
=||+||-||
=+-()
=2
(2)
=
=
=
【点评】 对于多重根式的化简,一般是设法将被开方数化成完全次方,再解答,或者用整体思想来解题.化简分母含有根式的式子时,将分子、分母同乘以分母的有理化因式即可,如本例(2)中,的分子、分母中同乘以.
举一反三:
【变式1】化简:(1);
(2)
【答案】(1);(2)。
类型二、指数运算、化简、求值
例2.用分数指数幂形式表示下列各式(式中):
(1);(2);(3);(4)。
【答案】;;;
【解析】先将根式写成分数指数幂的形式,再利用幂的运算性质化简即可。
(1)
(2);
(3);
(4)解法一:从里向外化为分数指数幂
==
=
=
=
解法二:从外向里化为分数指数幂。
=
==
=
=
【点评】此类问题应熟练应用。当所求根式含有多重根号时,要搞清被开方数,由里向外或由外向里,用分数指数幂写出,然后再用性质进行化简。
举一反三:
【变式1】把下列根式用指数形式表示出来,并化简
(1);
【答案】(1);(2)。
【变式2】把下列根式化成分数指数幂:
(1);(2);(3);(4)。
【答案】;;;
【解析】(1)=;
(2);
(3);
(4)=
=。
例3.计算:
(1);
(2)
(3)。
【答案】3;0;2
【解析】(1)原式=;
(2)原式=;
(3)原式=-5+6+4--(3-)=2;
【点评】(1)运算顺序(能否应用公式);(2)指数为负先化正;(3)根式化为分数指数幂.
举一反三:
【变式1】计算下列各式:
(1); (2).
【答案】(1)112 (2)
【解析】(1)原式=;
(2)原式.
例4.化简下列各式.
(1) ; (2); (3).
【答案】;;0.09
【解析】(1)即合并同类项的想法,常数与常数进行运算,同一字母的化为该字母的指数运算;(2)对字母运算的理解要求较高,即能够认出分数指数的完全平方关系;(3)具体数字的运算,学会如何简化运算.
(1)
(2)
(3)
举一反三:
【变式1】化简
【答案】
【解析】应注意到之间的关系,对分子使用乘法公式进行因式分解,
原式
.
【点评】根式的化简结果应写为最简根式.(1)被开方数的指数与根指数互质;(2)被开方数分母为1,且不含非正整数指数幂;(3)被开方数的每个因数的指数小于根指数.
【变式2】化简下列式子:
(1) (2) (3)
【答案】;;
【解析】(1)原式
(2)
∴由平方根的定义得:
(3)
.
例5.已知,求的值。
【答案】
【解析】从已知条件中解出的值,然后代入求值,这种方法是不可取的,而应设法从整体寻求结果与条件的联系,进而整体代入求值。
,,
,
=
=
【点评】对于“条件求值”问题一定要弄清已知与未知的联系,然后采用“整体代换”或“化简后代换”方法求值。本题的关键是先求及的值,然后整体代入。
举一反三:
【变式1】(1)已知2x+2-x=a(a为常数),求8x+8-x的值.
(2)已知x+y=12, xy=9,且x
【解析】(1)8x+8-x=23x+2-3x=(2x)3+(2-x)3
(2)
又∵ x+y=12, xy=9, ∴(x-y)2=(x+y)2-4xy=122-4×9=108.
又 ∵ x
(2)一般不采用分别把x, y, 2x的值求出来代入求值的方法,应先将原式进行分母有理化,并用乘法公式变形,把2x+2-x,x+y及xy整体代入后再求值.
例6.已知,求的值
【答案】
【解析】先把化成,然后利用“整体代换”的方法去求值.
由,所以
=
例7. 已知a=,b=9.求:
(1)
(2).
【解析】(1)原式=.÷[a·]?
= =a.?
∵a=,∴原式=3.?
(2)方法一 化去负指数后解.?
∵a=∴a+b=
方法二 利用运算性质解.?
∵a=∴a+b=
【巩固练习】
1.化简,结果是( )
A. B. C. D.
2. 计算的结果是( )
A.32 B.16 C. 64 D.128
3.若,且,则的值等于( )
A. B. C. D.2
4.下列各式中错误的是( )
A.
B.
C.
D.
5.、、这三个数的大小关系为( )
A. B. C. D.
6. 已知定义在上的奇函数和偶函数满足
,若,则( )
A. 2 B. C. D.
7. .
8.= .
9.若,则= .
10.已知,则= .
11.计算:
(1);
(2).
12.计算下列各式:
(1);
(2).
13. 计算: 14.已知.
求证:为定值.
15.(1)化简:;
(2)已知,求的值.
【答案与解析】
1. A 原式=
=
=
=
2. A ,故选A。
3. C 因为,所以,即.同理,又因为,所以,故.
4.D D中左边=
5. B ,,.,.
6.B 因为,又是奇函数,是偶函数,所以,所以,,两式联立解得,进一步求得.
7. 原式=.
8. 原式=.
9.-23 原式===4-27=-23.
10. 因为,所以.
11.解:(1)原式=.
(2)原式=
=
=
=
=
12.解:(1)原式=
=
=.
(2)原式=
=-()
=0
13. 原式=
=
=
=0
14.证明:
同理
原式=2,结论得证.
15.解:(1)原式==+
=
(2)因为,
所以 ,
所以
故当 a>b时, =a-b.当a=b时,=0.当a
