青岛版八年级数学下册6.2平行四边形的判定教学课件(2课时 共33张)
文档属性
| 名称 | 青岛版八年级数学下册6.2平行四边形的判定教学课件(2课时 共33张) |

|
|
| 格式 | zip | ||
| 文件大小 | 409.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-04 00:00:00 | ||
图片预览






文档简介
(共33张PPT)
教学课件
数学 八年级下册 青岛版
6.2 平行四边形的判定
第1课时
平行四边形的定义:两组对边分别平行的四边形叫
做平行四边形.
平行四边形的性质:对边相等,对角相等,对角线
互相平分.
?
判定
性质
定义
D
A
B
C
创设情景 明确目标
判定
性质
定义
D
A
B
C
问题 如何寻找平行四边形的判定方法?
直角三角
形的性质
直角三角
形的判定
勾股定理
勾股定理
的逆定理
在过去的学习中,类似的情况还有吗?请举例说明.
这些经验可以给我们怎样的启示?
1.经历平行四边形判定定理的猜想与证明过程,体
会类比思想及探究图形判定的一般思路;
2.掌握平行四边形的三个判定定理,能根据不同条件灵活选取适当的判定定理进行推理.
学习目标
两组对边分别相等的
四边形是平行四边形
平行四边形的性质
猜想
对边相等
对角相等
对角线互相平分
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
思考:这些猜想正确吗?
探究点一 平行四边形的判定定理
证明:连接BD.
∵AB =CD,AD =BC,
BD是公共边,
∴△ABD≌△CDB.
∴∠1=∠2,∠3=∠4.
∴AB∥DC,AD∥BC.
∴四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
判定定理1
猜想1
D
A
B
C
1
2
3
4
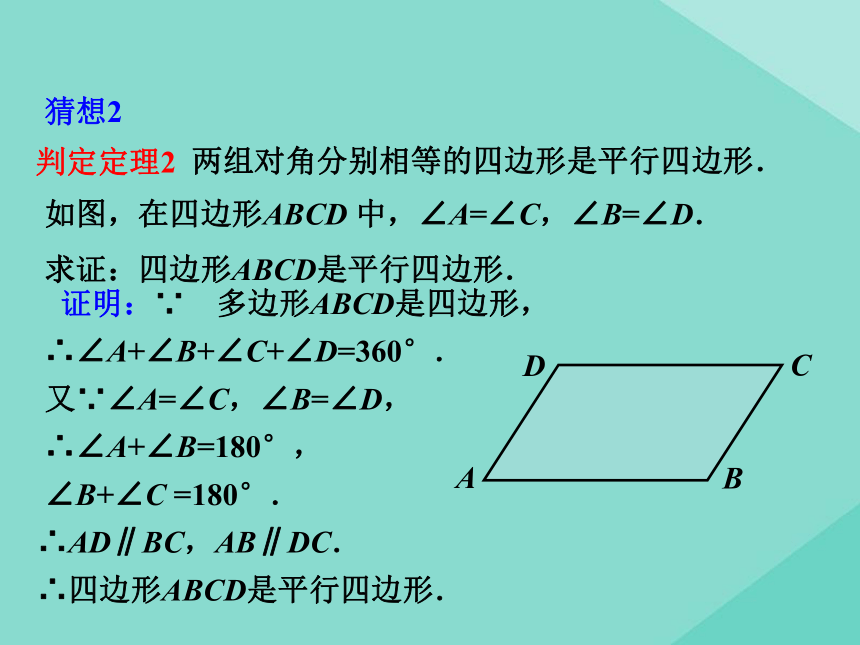
证明:∵ 多边形ABCD是四边形,
∴∠A+∠B+∠C+∠D=360°.
又∵∠A=∠C,∠B=∠D,
∴∠A+∠B=180°,
∠B+∠C =180°.
∴AD∥BC,AB∥DC.
∴四边形ABCD是平行四边形.
如图,在四边形ABCD 中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
两组对角分别相等的四边形是平行四边形.
判定定理2
猜想2
D
A
B
C
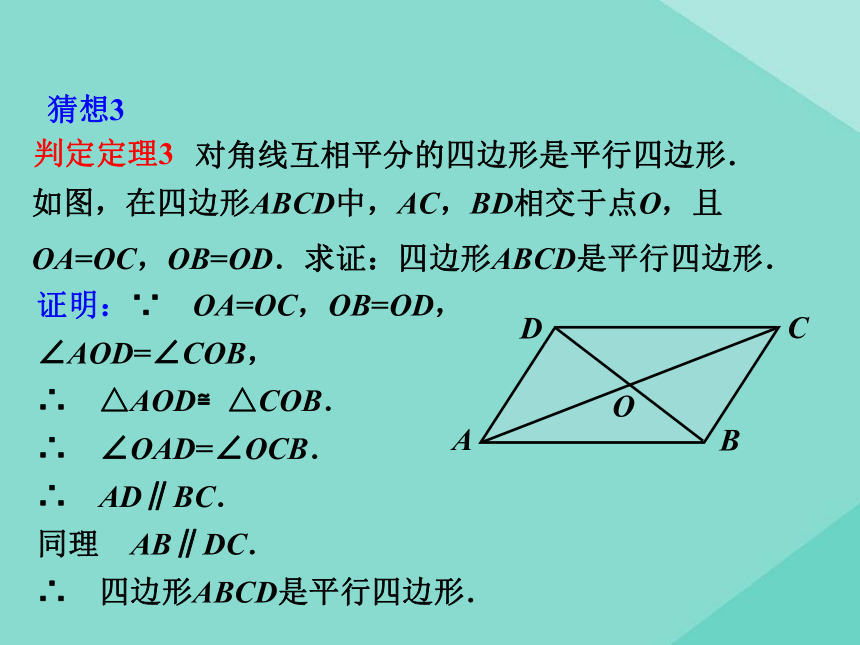
如图,在四边形ABCD中,AC,BD相交于点O,且
OA=OC,OB=OD.求证:四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
判定定理3
D
A
B
C
O
猜想3
证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴ △AOD≌△COB.
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形.
现在,我们一共有哪些判定平行四边形的方法呢?
定义:两组对边分别平行的四边形叫做平行四边形.
判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
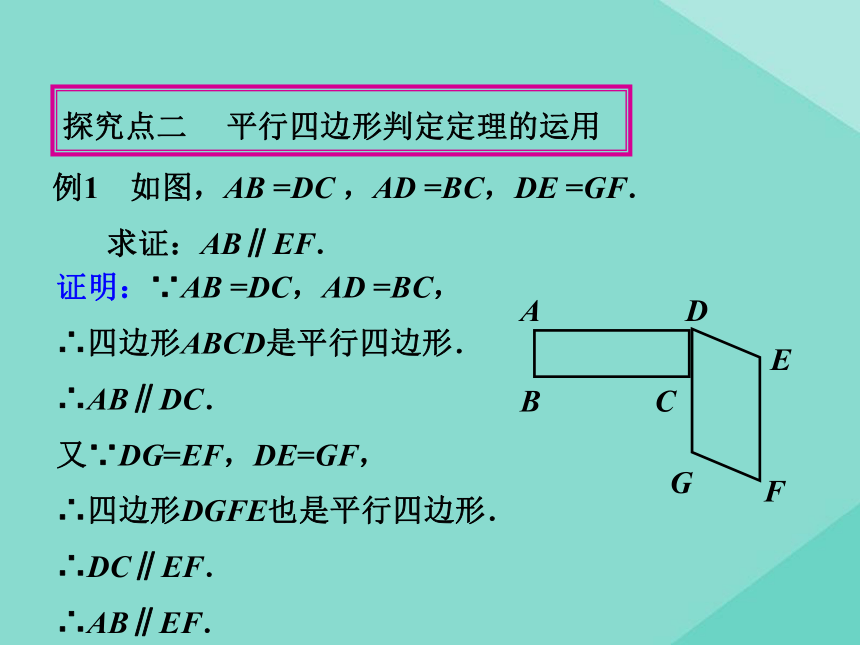
证明:∵AB =DC,AD =BC,
∴四边形ABCD是平行四边形.
∴AB∥DC.
又∵DG=EF,DE=GF,
∴四边形DGFE也是平行四边形.
∴DC∥EF.
∴AB∥EF.
探究点二 平行四边形判定定理的运用
例1 如图,AB =DC ,AD =BC,DE =GF.
求证:AB∥EF.
A
B
C
D
E
F
G
例2 如图,在 ABCD中,E,F分别是对角线AC 上的两点,并且 AE=CF.求证:四边形BFDE是平行四边形.
A
B
C
D
E
F
O
还有其他证明方法吗?
你更喜欢哪一种证法.
启示:
条件
对角线
简便的证明方法
边,角
A
B
C
D
E
F
变式练习
O
在上题中,若点E,F 分别在AC 两侧的延长线上,
如图,其他条件不变,结论还成立吗?请证明你的结论.
知识的角度:
平行四边形的判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
总结梳理 内化目标
过程与方法的角度:
研究图形的一般思路.
解题策略的角度:
证明平行四边形有多种方法,应根据条件灵活运用.
性质
定义
判定
逆向猜想
1、如图,在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,则当BC =___?cm,CD=___?cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,则当AO =__? _cm,DO=__? _cm时,四边形ABCD为平行四边形.
(1)
8
4
5
4
达标检测 反思目标
2、如图,口ABCD的对角线AC、BD相交于点O,E、F分别是OA,OC的中点.求证:BE=DF.
A
B
C
D
E
F
O
第2课时
如图,在下列各题中,再添上一个条件使结论成立:
(1)∵AB∥CD, ,
∴四边形ABCD是平行四边形.
(2)∵AB=CD, ,
∴四边形ABCD是平行四边形.
如果只考虑一组对边,它们满足
什么条件时,这个四边形能成为平行四边
形?
AD∥BC
AD=BC
A
B
C
D
创设情景 明确目标
1.掌握平行四边形的第四个判定定理,会综合运用
平行四边形的性质和判定进行推理和计算;
2.经历平行四边形判定定理的发现与证明过程,进
一步加深对平行四边形的认识.
学习目标
3.理解三角形中位线的概念,掌握三角形中位线定
理的内容;
探究点一 平行四边形的判定
猜想:一组对边平行且相等的四边形是平行四边形.
这个猜想正确吗?如何证明它?
定理:一组对边平行且相等的四边形是平行四边形.
现在你有多少种判定一个四边形是平行四边形的方法?
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(3)一组对边平行且相等的四边形是平行四边形;
(4)两组对角分别相等的四边形是平行四边形;
(5)对角线互相平分的四边形是平行四边形.
A
B
C
D
E
F
在上题中,将“E,F分别是AB,CD的中点”改为
“E,F分别是AB,CD上的点,且AE=CF”,结论是否
仍然成立?请说明理由.
练 习
例1 如图,在 ABCD中,E,F分别是AB,CD的
中点.求证:四边形EBFD是平行四边形.
如图,在△ABC中,D,E分别是边AB,AC 的中点,
连接DE. 像DE这样,连接三角形两边中点的线段叫做
三角形的中位线.
看一看,量一量,猜一猜:
DE与BC之间有什么位置关系和数量关系?
探究点二 三角形的中位线定理
我们在研究平行四边形时,经常采用把平行四边
形转化为三角形的问题,能否用平行四边形研究三角形呢?
A
B
C
D
E
A
B
C
D
E
你能对照图形写出已知、求证吗?
怎样分析证明思路?
请分别试一试,这些方案是否都可行.如可行,
说出辅助线的画法;如不可行,请说明原因.
请用适当的方法证明猜想.
请用自己的语言说出得到的结论,并比较证明方法
的异同.
三角形中位线定理:三角形的中位线平行于三角形
的第三边,并且等于第三边的一半.
在△ABC中,
∵ D,E分别是边AB,AC的中点,
∴ DE∥BC,且DE= BC .
证明猜想
A
B
C
D
E
如图,在△ABC中,∠C=90°,AC=8,CB=6,D,
E,F分别是BC,AC,AB的中点,则四边形AEDF的周
长为________;Rt△ABC的中位线分别是___________;
斜边上的中线是_______,其长为______.
18
DE,DF
CF
5
基础训练
A
B
C
D
E
F
1、判断题:
⑴相邻的两个角都互补的四边形是平行四边形. ( )
⑵两组对角分别相等的四边形是平行四边形. ( )
⑶一组对边平行,另一组对边相等的四边形是平行四边形 .( )
⑷一组对边平行且相等的四边形是平行四边形. ( )
⑸对角线相等的四边形是平行四边形. ( )
⑹对角线互相平分的四边形是平行四边形 . ( )
√
√
×
√
×
√
达标检测 反思目标
2、已知:如图,AC∥ED,点B在AC上,且AB=ED=BC, 找出图中的平行四边形,并说明理由 .
解:图中的平行四边形有 EDBA和 EDCB.
理由是:
同理可证四边形EDCB是平行四边形
∵ AC∥ED ( )
∴ ED ∥ ______
又∵ED = ______ ( )
∴四边形EDBA是平行四边形( )
已知
一组对边平行且相等的四边形是平行四边形
AB
AB
已知
3 如图,四边形AEFD和EBCF都是平行四边形.
求证:四边形ABCD是平行四边形.
A
B
C
D
E
F
4 如图,分别以Rt△ABC的直角边AC及斜边AB
向外作等边△ACD、等边△ABE.且∠BAC=30°,EF
⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
A
B
C
D
E
F
5 在四边形ABCD中,E,F,G,H分别是AB,
BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
A
B
C
D
E
F
H
G
两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形.
从角考虑 两组对角分别相等的四边形是平行四边形.
从对角线考虑 对角线互相平分的四边形是平行四边形.
从边
考虑
判定一个四边形是平行四边形可从哪些角度思考?
具体有哪些方法?
总结梳理 内化目标
教学课件
数学 八年级下册 青岛版
6.2 平行四边形的判定
第1课时
平行四边形的定义:两组对边分别平行的四边形叫
做平行四边形.
平行四边形的性质:对边相等,对角相等,对角线
互相平分.
?
判定
性质
定义
D
A
B
C
创设情景 明确目标
判定
性质
定义
D
A
B
C
问题 如何寻找平行四边形的判定方法?
直角三角
形的性质
直角三角
形的判定
勾股定理
勾股定理
的逆定理
在过去的学习中,类似的情况还有吗?请举例说明.
这些经验可以给我们怎样的启示?
1.经历平行四边形判定定理的猜想与证明过程,体
会类比思想及探究图形判定的一般思路;
2.掌握平行四边形的三个判定定理,能根据不同条件灵活选取适当的判定定理进行推理.
学习目标
两组对边分别相等的
四边形是平行四边形
平行四边形的性质
猜想
对边相等
对角相等
对角线互相平分
两组对角分别相等的
四边形是平行四边形
对角线互相平分的四
边形是平行四边形
思考:这些猜想正确吗?
探究点一 平行四边形的判定定理
证明:连接BD.
∵AB =CD,AD =BC,
BD是公共边,
∴△ABD≌△CDB.
∴∠1=∠2,∠3=∠4.
∴AB∥DC,AD∥BC.
∴四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
判定定理1
猜想1
D
A
B
C
1
2
3
4
证明:∵ 多边形ABCD是四边形,
∴∠A+∠B+∠C+∠D=360°.
又∵∠A=∠C,∠B=∠D,
∴∠A+∠B=180°,
∠B+∠C =180°.
∴AD∥BC,AB∥DC.
∴四边形ABCD是平行四边形.
如图,在四边形ABCD 中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
两组对角分别相等的四边形是平行四边形.
判定定理2
猜想2
D
A
B
C
如图,在四边形ABCD中,AC,BD相交于点O,且
OA=OC,OB=OD.求证:四边形ABCD是平行四边形.
对角线互相平分的四边形是平行四边形.
判定定理3
D
A
B
C
O
猜想3
证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴ △AOD≌△COB.
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形.
现在,我们一共有哪些判定平行四边形的方法呢?
定义:两组对边分别平行的四边形叫做平行四边形.
判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
证明:∵AB =DC,AD =BC,
∴四边形ABCD是平行四边形.
∴AB∥DC.
又∵DG=EF,DE=GF,
∴四边形DGFE也是平行四边形.
∴DC∥EF.
∴AB∥EF.
探究点二 平行四边形判定定理的运用
例1 如图,AB =DC ,AD =BC,DE =GF.
求证:AB∥EF.
A
B
C
D
E
F
G
例2 如图,在 ABCD中,E,F分别是对角线AC 上的两点,并且 AE=CF.求证:四边形BFDE是平行四边形.
A
B
C
D
E
F
O
还有其他证明方法吗?
你更喜欢哪一种证法.
启示:
条件
对角线
简便的证明方法
边,角
A
B
C
D
E
F
变式练习
O
在上题中,若点E,F 分别在AC 两侧的延长线上,
如图,其他条件不变,结论还成立吗?请证明你的结论.
知识的角度:
平行四边形的判定定理:
(1)两组对边分别相等的四边形是平行四边形;
(2)两组对角分别相等的四边形是平行四边形;
(3)对角线互相平分的四边形是平行四边形.
总结梳理 内化目标
过程与方法的角度:
研究图形的一般思路.
解题策略的角度:
证明平行四边形有多种方法,应根据条件灵活运用.
性质
定义
判定
逆向猜想
1、如图,在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,则当BC =___?cm,CD=___?cm时,四边形ABCD为平行四边形;
(2)若AC=10cm,BD=8cm,则当AO =__? _cm,DO=__? _cm时,四边形ABCD为平行四边形.
(1)
8
4
5
4
达标检测 反思目标
2、如图,口ABCD的对角线AC、BD相交于点O,E、F分别是OA,OC的中点.求证:BE=DF.
A
B
C
D
E
F
O
第2课时
如图,在下列各题中,再添上一个条件使结论成立:
(1)∵AB∥CD, ,
∴四边形ABCD是平行四边形.
(2)∵AB=CD, ,
∴四边形ABCD是平行四边形.
如果只考虑一组对边,它们满足
什么条件时,这个四边形能成为平行四边
形?
AD∥BC
AD=BC
A
B
C
D
创设情景 明确目标
1.掌握平行四边形的第四个判定定理,会综合运用
平行四边形的性质和判定进行推理和计算;
2.经历平行四边形判定定理的发现与证明过程,进
一步加深对平行四边形的认识.
学习目标
3.理解三角形中位线的概念,掌握三角形中位线定
理的内容;
探究点一 平行四边形的判定
猜想:一组对边平行且相等的四边形是平行四边形.
这个猜想正确吗?如何证明它?
定理:一组对边平行且相等的四边形是平行四边形.
现在你有多少种判定一个四边形是平行四边形的方法?
(1)两组对边分别平行的四边形是平行四边形;
(2)两组对边分别相等的四边形是平行四边形;
(3)一组对边平行且相等的四边形是平行四边形;
(4)两组对角分别相等的四边形是平行四边形;
(5)对角线互相平分的四边形是平行四边形.
A
B
C
D
E
F
在上题中,将“E,F分别是AB,CD的中点”改为
“E,F分别是AB,CD上的点,且AE=CF”,结论是否
仍然成立?请说明理由.
练 习
例1 如图,在 ABCD中,E,F分别是AB,CD的
中点.求证:四边形EBFD是平行四边形.
如图,在△ABC中,D,E分别是边AB,AC 的中点,
连接DE. 像DE这样,连接三角形两边中点的线段叫做
三角形的中位线.
看一看,量一量,猜一猜:
DE与BC之间有什么位置关系和数量关系?
探究点二 三角形的中位线定理
我们在研究平行四边形时,经常采用把平行四边
形转化为三角形的问题,能否用平行四边形研究三角形呢?
A
B
C
D
E
A
B
C
D
E
你能对照图形写出已知、求证吗?
怎样分析证明思路?
请分别试一试,这些方案是否都可行.如可行,
说出辅助线的画法;如不可行,请说明原因.
请用适当的方法证明猜想.
请用自己的语言说出得到的结论,并比较证明方法
的异同.
三角形中位线定理:三角形的中位线平行于三角形
的第三边,并且等于第三边的一半.
在△ABC中,
∵ D,E分别是边AB,AC的中点,
∴ DE∥BC,且DE= BC .
证明猜想
A
B
C
D
E
如图,在△ABC中,∠C=90°,AC=8,CB=6,D,
E,F分别是BC,AC,AB的中点,则四边形AEDF的周
长为________;Rt△ABC的中位线分别是___________;
斜边上的中线是_______,其长为______.
18
DE,DF
CF
5
基础训练
A
B
C
D
E
F
1、判断题:
⑴相邻的两个角都互补的四边形是平行四边形. ( )
⑵两组对角分别相等的四边形是平行四边形. ( )
⑶一组对边平行,另一组对边相等的四边形是平行四边形 .( )
⑷一组对边平行且相等的四边形是平行四边形. ( )
⑸对角线相等的四边形是平行四边形. ( )
⑹对角线互相平分的四边形是平行四边形 . ( )
√
√
×
√
×
√
达标检测 反思目标
2、已知:如图,AC∥ED,点B在AC上,且AB=ED=BC, 找出图中的平行四边形,并说明理由 .
解:图中的平行四边形有 EDBA和 EDCB.
理由是:
同理可证四边形EDCB是平行四边形
∵ AC∥ED ( )
∴ ED ∥ ______
又∵ED = ______ ( )
∴四边形EDBA是平行四边形( )
已知
一组对边平行且相等的四边形是平行四边形
AB
AB
已知
3 如图,四边形AEFD和EBCF都是平行四边形.
求证:四边形ABCD是平行四边形.
A
B
C
D
E
F
4 如图,分别以Rt△ABC的直角边AC及斜边AB
向外作等边△ACD、等边△ABE.且∠BAC=30°,EF
⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
A
B
C
D
E
F
5 在四边形ABCD中,E,F,G,H分别是AB,
BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
A
B
C
D
E
F
H
G
两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形.
从角考虑 两组对角分别相等的四边形是平行四边形.
从对角线考虑 对角线互相平分的四边形是平行四边形.
从边
考虑
判定一个四边形是平行四边形可从哪些角度思考?
具体有哪些方法?
总结梳理 内化目标
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
