青岛版八年级数学下册6.3特殊的平行四边形教学课件(2课时 共38张)
文档属性
| 名称 | 青岛版八年级数学下册6.3特殊的平行四边形教学课件(2课时 共38张) |

|
|
| 格式 | zip | ||
| 文件大小 | 881.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-04 00:00:00 | ||
图片预览






文档简介
(共38张PPT)
教学课件
数学 八年级下册 青岛版
6.3 特殊的平行四边形
第一课时 矩形
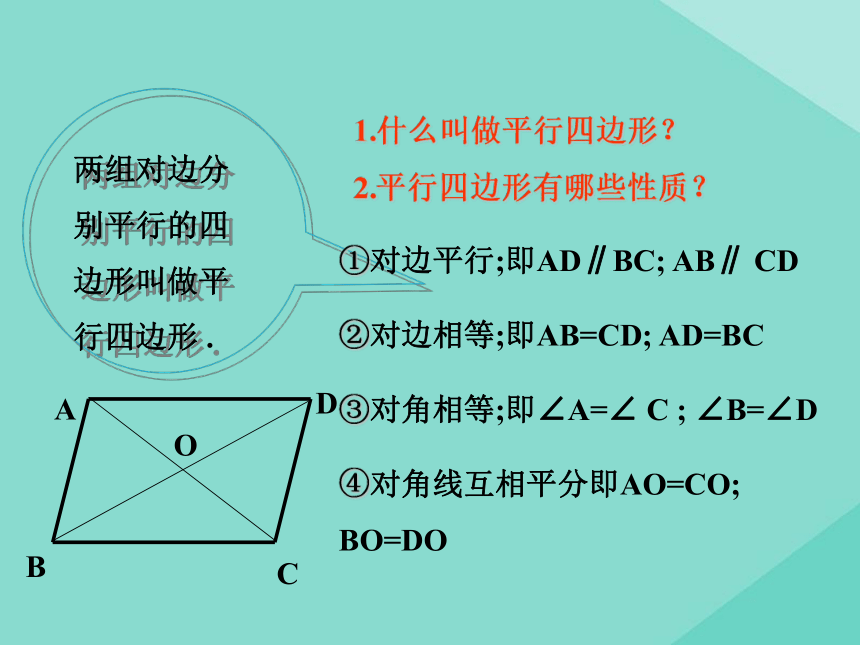
1.什么叫做平行四边形?
2.平行四边形有哪些性质?
A
B
C
D
两组对边分别平行的四边形叫做平行四边形 .
O
①对边平行;即AD∥BC; AB∥ CD
②对边相等;即AB=CD; AD=BC
③对角相等;即∠A=∠ C ; ∠B=∠D
④对角线互相平分即AO=CO; BO=DO
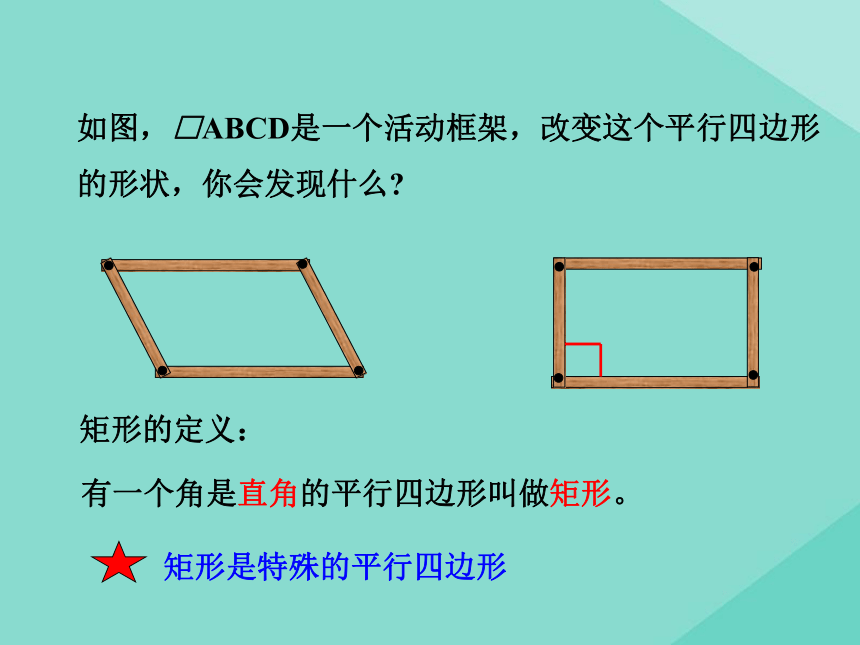
如图,□ABCD是一个活动框架,改变这个平行四边形的形状,你会发现什么?
有一个角是直角的平行四边形叫做矩形。
矩形的定义:
矩形是特殊的平行四边形
具备平行四边形所有的性质
A
B
C
D
O
角
边
对角线
对边平行且相等
对角相等 ,邻角互补
对角线互相平分
矩形的一般性质:
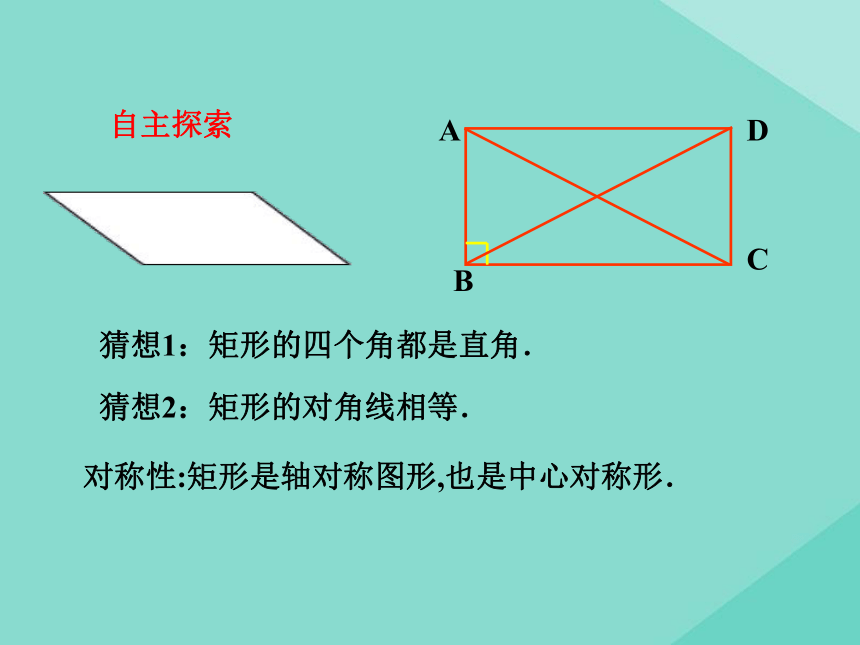
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
B
A
D
C
自主探索
对称性:矩形是轴对称图形,也是中心对称形.
A
B
C
D
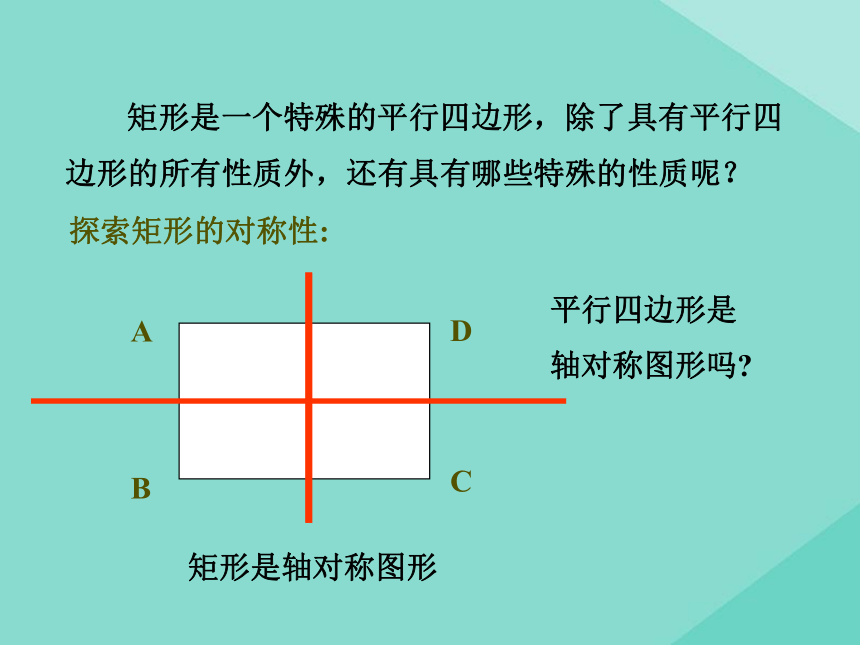
探索矩形的对称性:
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有具有哪些特殊的性质呢?
矩形是轴对称图形
平行四边形是轴对称图形吗?
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°.
A
B
C
D
证明: ∵四边形ABCD是矩形,
∴ ∠A=90°.
∵矩形ABCD是平行四边形,
∴ AD//BC, ∠A=∠C,∠B=∠D.
∵ ∠A +∠B =180°,
∴ ∠A=∠B=∠C=∠D=90°.
说明:矩形的四个角都是直角
已知:如图,四边形ABCD是矩形,
求证:AC = BD.
A
B
C
D
证明:∵四边形ABCD是矩形,
∴∠ABC = ∠DCB = 90°,
AB = DC .
又∵BC = CB,
∴△ABC≌△DCB,
∴AC = BD. 说明:矩形的对角线相等
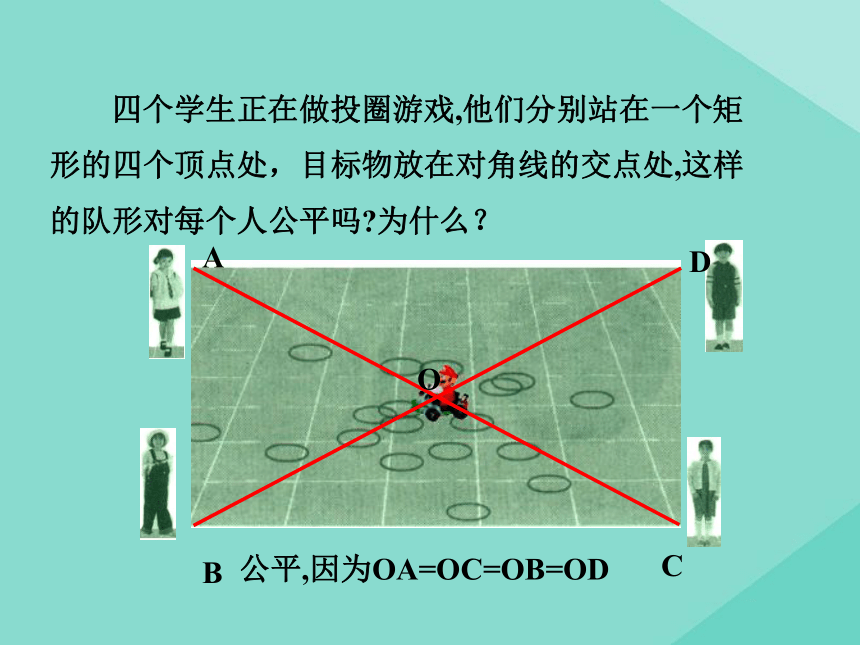
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
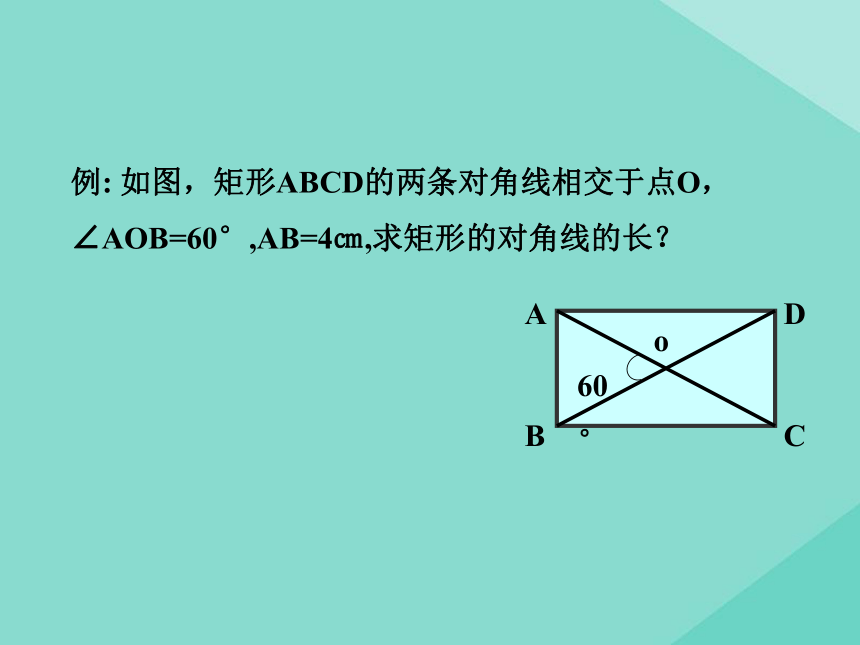
例: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形的对角线的长?
D
C
B
A
o
60°
方法小结: 如果矩形的两条对角 线的夹角是60°或120°, 那么其中必有等边三角形.
∴AC与BD相等且互相平分,
∴ OA=OB.
∵ ∠AOB=60°,
∴ △AOB是等边三角形,
∴ OA=AB=4(㎝),
∴ 矩形的对角线的长 AC=BD=2OA=8(㎝).
解:∵ 四边形ABCD是矩形,
D
C
B
A
o
60°
×
√
×
√
√
练习1 现在你能帮小明解决问题了吗?小明判定
相框为矩形的下列方法,哪些正确?为什么?
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都相等的四边形是矩形;( )
(3)对角线相等的四边形是矩形;( )
(4)对角线互相平分且相等的四边形是矩形;( )
(5)两组对边分别平行,且对角线相等的四边形是矩
形.( )
练习2 在“?”号处填上恰当的条件:
四边形
平行四边形
矩形
?
?
?
练习3.已知:四边形ABCD是矩形
(1).若AB=8㎝,AD=6㎝,则AC=_______ ㎝ ,
OB=_______ ㎝.
(2).若 ∠DOC=120°,AC=8㎝,则AD= _____cm,
AB= _____cm.
O
D
C
B
A
5
10
4
直角三角形斜边上的中线等于斜边的一半.
矩形是轴对称图形,连接对边中点的直线是它的两
条对称轴.
矩形
矩形的对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分.
矩形:有一个角是直角的平行四边形叫做矩形.
第二课时
学习目标:
1.理解菱形的概念,会用菱形的性质解决简单的问题;
2.经历类比矩形探究菱形性质的过程,通过观察、类比、
猜想、证明等活动,体会几何图形研究的一般步骤和
方法.
学习重点:
菱形性质的探索、证明和运用.
2000多年前……
一把埋藏在地下的古剑,出土时依然寒气逼人,毫无锈蚀,锋利无比,稍一用力,便可将多层白纸划破,剑身上整齐排列着黑色菱形暗纹——越王勾践剑
小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?从这个图形中你有什么发现?
如何利用折纸、剪切的方法,能够既快又准确地剪出一个菱形的纸片?
剪一剪
1、菱形是___ _的平行四边形,它具有
的所有性质.
2、菱形的特殊性质.
(1)边:菱形的四条边都 ;
(2)对角线:菱形的两条对角线 ,
并且每一条对角线 _______ ;
(3)对称性:菱形是 对称图形, 它的对称轴
就是对角线所在的直线.
特殊
平行四边形
相等
互相垂直平分
平分一组对角
轴
3、如下图,根据菱形的性质,在菱形ABCD中,
(1)AB= = = ;
(2)AC⊥ ,且AO= ,BO= ;
∠ABO= ,∠BCO= ,
∠CDO= ,∠DAO= .
O
思考 : 如何证明菱形的性质?说一说
你的证明思路.
BC
CD
DA
BD
CO
DO
∠CBO
∠DCO
∠ADO
∠BAO
已知:如图,四边形ABCD是菱形.
A
B
C
D
O
证明:(1)∵四边形ABCD是菱形,
∴DA=AB(菱形的定义),
OD=OB (平行四边形的对角线互相平分),
∴ AC ⊥ DB ,
AC平分∠DAB(三线合一).
同理: AC平分∠DCB ;
DB平分∠ADC和∠ABC.
AC⊥BD,
AC平分∠DAB和∠DCB,
BD平分∠ADC和∠ABC.
求证:
例:四边形ABCD是菱形,对角线AC、BD相交于
点O,且AB=5,AO=4.求AC和BD的长.
O
解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD, AC⊥BD.
∵在Rt△AOB中,OB2+OA2=AB2,
AB=5cm,AO=4cm,
∴OB=3cm.
∴BD=2OB=6cm, AC=2OA=8cm.
1、菱形具有而平行四边形不具有的性质是( )
(A)对角线互相平分
(B)对角线相等
(C)对角线互相垂直且相等
(D)对角线互相垂直,每一条对角线平分一组对角
2、已知菱形的周长是12cm,那么它的边长是________.
D
3cm
3 、如图,菱形花坛ABCD的边长为20 m,∠ABC=60°,
沿着菱形的对角线修建了两条小路AC和BD.求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
A
B
C
D
O
第三课时
矩形 菱形
性质 1.四个角都________ 1.四条边都_______
2.对角线__________ 2.对角线互相_________
且平分每组________
判定 1.有一个角是______的
___________ 1.有一组邻边______的
__________
2.有三个角是_____的
_________ 2.对角线互相______的
________
3.对角线________的
__________ 3.四条边_______的
________
相等
直角
相等
相等
平行四边形
直角
对角
互相平分
相等
垂直
平行四边形
相等
平行四边形
垂直
四边形
平行四边形
四边形
有一个角为直角
有一组邻边相等
有一组邻边
相等
有一个角是直角
问题提出
1.有一组邻边相等的矩形是一个什么样的图形?
2.有一个角是直角的菱形是一个什么样的图形?
1、四条边_______,四个角都是_______的四边形叫做正方形.
2、正方形既是_____形,又是_____形.即
(1)有一组________相等的矩形是正方形.
(2)有一个角是________的菱形是正方形.
相等
直角
矩
菱
直角
邻边
归纳:
1.正方形的定义:四个角都是直角,且四条边都相等的
四边形是正方形.
3.正方形既是矩形,也是菱形,同时也是特殊的平行四边形.
思考
正方形有什么样的性质,以及如何去判定一个正方形呢?
2.有一组邻边相等的矩形是正方形;
有一个角是直角的菱形是正方形.
例1 (1)把一张长方形纸片按如图的方式折一下,就可以裁出正方形纸片.为什么?
(2)如何从一块长方形木板中裁出一块最大的正方形木板呢?
解:由已知,对折后,所得的四边形有三个
直角,且一组邻边相等,所以可以裁出正方
形纸片.
解:在长方形最长的两边,截取长度等于“长方形的短边的长度”,这样就可以截出面积最大的正方形.
例2、 根据图形所具有的性质,在下表相应的空格中打“√”
平行四边形 矩形 菱形 正方形
对边平行且相等
四条边都相等
四个角都是直角
对角线互相平分 √
对角线互相垂直
对角线相等
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
作比较
请比较一般四边形,平行四边形,矩形,菱形,正方形的对角线的性质.
对边平行且相等
四边形
平行四边形
矩形
菱形
对角线平分且相等
对角线平分且垂直
正方形
对角线互
相平分
对角线相等
对角线互
相垂直
对角线相等且
垂直平分
对角线平分,相等且垂直(对角线法)
1、如图,ABCD是一块正方形场地.小华和小芳在AB边上取定了一点E,测量知,EC=30m,EB=10m.则这块场地的面积和对角线分别是多少?
解:根据勾股定理,得
BC2=EC2-EB2
=302-102
=800.
∴BC= .
∴这块场地的面积为 =800 ( ).
∴ 对角线 为40m.
2、满足下列条件的四边形是不是正方形?为什么?
(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分且相等的四边形.
解:(1)根据正方形的性质可知,该平行四边形是正方形.
(2)根据正方形的性质可知,该矩形是正方形.
(3)根据正方形的性质可知,该菱形是正方形.
(4)根据正方形的性质可知,该四边形是正方形.
已知:如图,在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC于点E,DF⊥AC于点F.求证:四边形CFDE是正方形.
解:∵∠ACB=90°,DE⊥BC于点E,
DF⊥AC于点F.
∴四边形CEDF有三个直角,它是矩形.
又∵CD平分∠ACB,根据角平分线上的点到两边的距离都相等可知,DE=DF,
∴矩形CEDF有一组邻边相等.
根据正方形的判定方法知,四边形CEDF是正方形.
现在,你对正方形有哪些新的认识?
正方形既是矩形又是菱形.
一个角是直角
一组邻边相等
平行四边
形
矩形
菱形
一组邻边相等
一个角是直角
正方形
教学课件
数学 八年级下册 青岛版
6.3 特殊的平行四边形
第一课时 矩形
1.什么叫做平行四边形?
2.平行四边形有哪些性质?
A
B
C
D
两组对边分别平行的四边形叫做平行四边形 .
O
①对边平行;即AD∥BC; AB∥ CD
②对边相等;即AB=CD; AD=BC
③对角相等;即∠A=∠ C ; ∠B=∠D
④对角线互相平分即AO=CO; BO=DO
如图,□ABCD是一个活动框架,改变这个平行四边形的形状,你会发现什么?
有一个角是直角的平行四边形叫做矩形。
矩形的定义:
矩形是特殊的平行四边形
具备平行四边形所有的性质
A
B
C
D
O
角
边
对角线
对边平行且相等
对角相等 ,邻角互补
对角线互相平分
矩形的一般性质:
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
B
A
D
C
自主探索
对称性:矩形是轴对称图形,也是中心对称形.
A
B
C
D
探索矩形的对称性:
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有具有哪些特殊的性质呢?
矩形是轴对称图形
平行四边形是轴对称图形吗?
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°.
A
B
C
D
证明: ∵四边形ABCD是矩形,
∴ ∠A=90°.
∵矩形ABCD是平行四边形,
∴ AD//BC, ∠A=∠C,∠B=∠D.
∵ ∠A +∠B =180°,
∴ ∠A=∠B=∠C=∠D=90°.
说明:矩形的四个角都是直角
已知:如图,四边形ABCD是矩形,
求证:AC = BD.
A
B
C
D
证明:∵四边形ABCD是矩形,
∴∠ABC = ∠DCB = 90°,
AB = DC .
又∵BC = CB,
∴△ABC≌△DCB,
∴AC = BD. 说明:矩形的对角线相等
四个学生正在做投圈游戏,他们分别站在一个矩形的四个顶点处,目标物放在对角线的交点处,这样的队形对每个人公平吗?为什么?
O
A
B
C
D
公平,因为OA=OC=OB=OD
例: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形的对角线的长?
D
C
B
A
o
60°
方法小结: 如果矩形的两条对角 线的夹角是60°或120°, 那么其中必有等边三角形.
∴AC与BD相等且互相平分,
∴ OA=OB.
∵ ∠AOB=60°,
∴ △AOB是等边三角形,
∴ OA=AB=4(㎝),
∴ 矩形的对角线的长 AC=BD=2OA=8(㎝).
解:∵ 四边形ABCD是矩形,
D
C
B
A
o
60°
×
√
×
√
√
练习1 现在你能帮小明解决问题了吗?小明判定
相框为矩形的下列方法,哪些正确?为什么?
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都相等的四边形是矩形;( )
(3)对角线相等的四边形是矩形;( )
(4)对角线互相平分且相等的四边形是矩形;( )
(5)两组对边分别平行,且对角线相等的四边形是矩
形.( )
练习2 在“?”号处填上恰当的条件:
四边形
平行四边形
矩形
?
?
?
练习3.已知:四边形ABCD是矩形
(1).若AB=8㎝,AD=6㎝,则AC=_______ ㎝ ,
OB=_______ ㎝.
(2).若 ∠DOC=120°,AC=8㎝,则AD= _____cm,
AB= _____cm.
O
D
C
B
A
5
10
4
直角三角形斜边上的中线等于斜边的一半.
矩形是轴对称图形,连接对边中点的直线是它的两
条对称轴.
矩形
矩形的对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且互相平分.
矩形:有一个角是直角的平行四边形叫做矩形.
第二课时
学习目标:
1.理解菱形的概念,会用菱形的性质解决简单的问题;
2.经历类比矩形探究菱形性质的过程,通过观察、类比、
猜想、证明等活动,体会几何图形研究的一般步骤和
方法.
学习重点:
菱形性质的探索、证明和运用.
2000多年前……
一把埋藏在地下的古剑,出土时依然寒气逼人,毫无锈蚀,锋利无比,稍一用力,便可将多层白纸划破,剑身上整齐排列着黑色菱形暗纹——越王勾践剑
小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?从这个图形中你有什么发现?
如何利用折纸、剪切的方法,能够既快又准确地剪出一个菱形的纸片?
剪一剪
1、菱形是___ _的平行四边形,它具有
的所有性质.
2、菱形的特殊性质.
(1)边:菱形的四条边都 ;
(2)对角线:菱形的两条对角线 ,
并且每一条对角线 _______ ;
(3)对称性:菱形是 对称图形, 它的对称轴
就是对角线所在的直线.
特殊
平行四边形
相等
互相垂直平分
平分一组对角
轴
3、如下图,根据菱形的性质,在菱形ABCD中,
(1)AB= = = ;
(2)AC⊥ ,且AO= ,BO= ;
∠ABO= ,∠BCO= ,
∠CDO= ,∠DAO= .
O
思考 : 如何证明菱形的性质?说一说
你的证明思路.
BC
CD
DA
BD
CO
DO
∠CBO
∠DCO
∠ADO
∠BAO
已知:如图,四边形ABCD是菱形.
A
B
C
D
O
证明:(1)∵四边形ABCD是菱形,
∴DA=AB(菱形的定义),
OD=OB (平行四边形的对角线互相平分),
∴ AC ⊥ DB ,
AC平分∠DAB(三线合一).
同理: AC平分∠DCB ;
DB平分∠ADC和∠ABC.
AC⊥BD,
AC平分∠DAB和∠DCB,
BD平分∠ADC和∠ABC.
求证:
例:四边形ABCD是菱形,对角线AC、BD相交于
点O,且AB=5,AO=4.求AC和BD的长.
O
解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD, AC⊥BD.
∵在Rt△AOB中,OB2+OA2=AB2,
AB=5cm,AO=4cm,
∴OB=3cm.
∴BD=2OB=6cm, AC=2OA=8cm.
1、菱形具有而平行四边形不具有的性质是( )
(A)对角线互相平分
(B)对角线相等
(C)对角线互相垂直且相等
(D)对角线互相垂直,每一条对角线平分一组对角
2、已知菱形的周长是12cm,那么它的边长是________.
D
3cm
3 、如图,菱形花坛ABCD的边长为20 m,∠ABC=60°,
沿着菱形的对角线修建了两条小路AC和BD.求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
A
B
C
D
O
第三课时
矩形 菱形
性质 1.四个角都________ 1.四条边都_______
2.对角线__________ 2.对角线互相_________
且平分每组________
判定 1.有一个角是______的
___________ 1.有一组邻边______的
__________
2.有三个角是_____的
_________ 2.对角线互相______的
________
3.对角线________的
__________ 3.四条边_______的
________
相等
直角
相等
相等
平行四边形
直角
对角
互相平分
相等
垂直
平行四边形
相等
平行四边形
垂直
四边形
平行四边形
四边形
有一个角为直角
有一组邻边相等
有一组邻边
相等
有一个角是直角
问题提出
1.有一组邻边相等的矩形是一个什么样的图形?
2.有一个角是直角的菱形是一个什么样的图形?
1、四条边_______,四个角都是_______的四边形叫做正方形.
2、正方形既是_____形,又是_____形.即
(1)有一组________相等的矩形是正方形.
(2)有一个角是________的菱形是正方形.
相等
直角
矩
菱
直角
邻边
归纳:
1.正方形的定义:四个角都是直角,且四条边都相等的
四边形是正方形.
3.正方形既是矩形,也是菱形,同时也是特殊的平行四边形.
思考
正方形有什么样的性质,以及如何去判定一个正方形呢?
2.有一组邻边相等的矩形是正方形;
有一个角是直角的菱形是正方形.
例1 (1)把一张长方形纸片按如图的方式折一下,就可以裁出正方形纸片.为什么?
(2)如何从一块长方形木板中裁出一块最大的正方形木板呢?
解:由已知,对折后,所得的四边形有三个
直角,且一组邻边相等,所以可以裁出正方
形纸片.
解:在长方形最长的两边,截取长度等于“长方形的短边的长度”,这样就可以截出面积最大的正方形.
例2、 根据图形所具有的性质,在下表相应的空格中打“√”
平行四边形 矩形 菱形 正方形
对边平行且相等
四条边都相等
四个角都是直角
对角线互相平分 √
对角线互相垂直
对角线相等
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
作比较
请比较一般四边形,平行四边形,矩形,菱形,正方形的对角线的性质.
对边平行且相等
四边形
平行四边形
矩形
菱形
对角线平分且相等
对角线平分且垂直
正方形
对角线互
相平分
对角线相等
对角线互
相垂直
对角线相等且
垂直平分
对角线平分,相等且垂直(对角线法)
1、如图,ABCD是一块正方形场地.小华和小芳在AB边上取定了一点E,测量知,EC=30m,EB=10m.则这块场地的面积和对角线分别是多少?
解:根据勾股定理,得
BC2=EC2-EB2
=302-102
=800.
∴BC= .
∴这块场地的面积为 =800 ( ).
∴ 对角线 为40m.
2、满足下列条件的四边形是不是正方形?为什么?
(1)对角线互相垂直且相等的平行四边形;
(2)对角线互相垂直的矩形;
(3)对角线相等的菱形;
(4)对角线互相垂直平分且相等的四边形.
解:(1)根据正方形的性质可知,该平行四边形是正方形.
(2)根据正方形的性质可知,该矩形是正方形.
(3)根据正方形的性质可知,该菱形是正方形.
(4)根据正方形的性质可知,该四边形是正方形.
已知:如图,在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC于点E,DF⊥AC于点F.求证:四边形CFDE是正方形.
解:∵∠ACB=90°,DE⊥BC于点E,
DF⊥AC于点F.
∴四边形CEDF有三个直角,它是矩形.
又∵CD平分∠ACB,根据角平分线上的点到两边的距离都相等可知,DE=DF,
∴矩形CEDF有一组邻边相等.
根据正方形的判定方法知,四边形CEDF是正方形.
现在,你对正方形有哪些新的认识?
正方形既是矩形又是菱形.
一个角是直角
一组邻边相等
平行四边
形
矩形
菱形
一组邻边相等
一个角是直角
正方形
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
