2019-2020学年江西省吉安市高一(上)期末数学试卷(Word版含答案)
文档属性
| 名称 | 2019-2020学年江西省吉安市高一(上)期末数学试卷(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 292.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-04 10:27:01 | ||
图片预览




文档简介
2019-2020学年江西省吉安市高一(上)期末数学试卷
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)已知A={x|﹣1<x<3},B={x|0<x﹣1<1},则A∪B=( )
A.(﹣∞,+∞) B.(1,2) C.(﹣1,3) D.(1,3)
2.(5分)函数的定义域为( )
A.(﹣2,1] B.(﹣∞,﹣2)∪(﹣2,1)
C.(﹣2,1) D.(﹣∞,﹣2)∪(﹣2,1]
3.(5分)设,b=log23,,则a,b,c的大小关系是( )
A.a<c<b B.c<a<b C.b<c<a D.c<b<a
4.(5分)已知角α的终边与单位圆交于点,则=( )
A. B.或 C.或 D.
5.(5分)函数f(x)=﹣2x2﹣(2a+1)x+3在区间[2,3]上是增函数,则a的取值范围是( )
A. B. C. D.
6.(5分)已知,,则=( )
A.1 B.2 C. D.
7.(5分)已知a>0,设函数(x∈[﹣a,a])的最大值为M,最小值为N,那么M+N+f(2020)+f(﹣2020)=( )
A.1 B.2 C.3 D.4
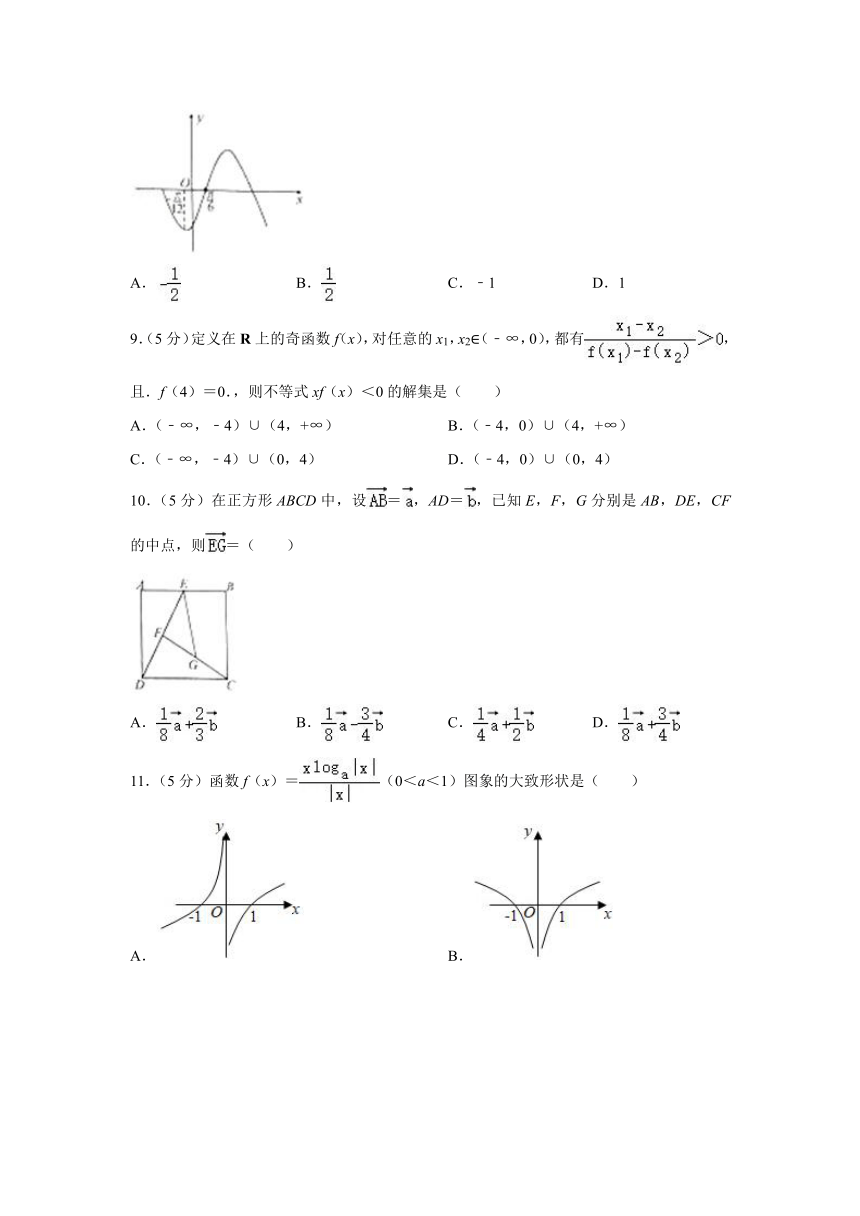
8.(5分)函数f(x)=2cos(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示,则=( )
A. B. C.﹣1 D.1
9.(5分)定义在R上的奇函数f(x),对任意的x1,x2∈(﹣∞,0),都有,且.f(4)=0.,则不等式xf(x)<0的解集是( )
A.(﹣∞,﹣4)∪(4,+∞) B.(﹣4,0)∪(4,+∞)
C.(﹣∞,﹣4)∪(0,4) D.(﹣4,0)∪(0,4)
10.(5分)在正方形ABCD中,设=,AD=,已知E,F,G分别是AB,DE,CF的中点,则=( )
A. B. C. D.
11.(5分)函数f(x)=(0<a<1)图象的大致形状是( )
A. B.
C. D.
12.(5分)已知f(x)是定义在R上的奇函数,且满足f(x+2)+f(x)=0,当x∈[0,1]时,f(x)=x2,则函数g(x)=xf(x)﹣1在区间[﹣6,6]上所有零点的个数为( )
A.0 B.2 C.4 D.6
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.(5分)已知||=2,||=3,,的夹角为60°,则|4﹣|= .
14.(5分)已知,且,则的值为 .
15.(5分)在矩形ABCD中,AB=1,BC=2,P是直线AD上的动点(端点可取),则的取值范围是 .
16.(5分)新能源汽车包括纯电动汽车、增程式电动汽车、混合动力汽车、燃料电池电动汽车、氢发动机汽车、其他新能源汽车等.它是未来汽车的发展方向.一个新能源汽车制造厂引进了一条新能源汽车整车装配流水线,这条流水线生产的新能源汽车数量x(辆)与创造的价值y(万元)之间满足二次函数关系.已知产量为0时,创造的价值也为0;当产量为40000辆时,创造的价值达到最大6000万元.若这家工厂希望利用这条流水线创收达到56250万元,则它可能生产的新能源汽车数量是 辆.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知全集U=R,A={x|3x≤9},B={x|a+x≤0},C={x|0<log2x≤2}.
(1)当a=1时,求A∩(?UB);
(2)若C?B,求实数a的取值范围.
18.已知函数.
(1)求f(x)的最小正周期;
(2)求f(x)的单调递减区间以及在区间上的最值.
19.定义在(﹣∞,0)∪(0,+∞)上的函数y=f(x)满足,且函数f(x)在(﹣∞,0)上是减函数.
(1)求f(﹣1),并证明函数y=f(x)是偶函数;
(2)若f(2)=1,解不等式.
20.第七届世界军人运动会(7thCISMMilitaryWorldGames),简称“武汉军运会”,于2019年10月18日至27日在中国武汉举行,共设置射击、游泳、田径篮球等27个大项、329个小项.来自100多个国家的近万名现役军人同台竞技.会议期间,某公司欲采购海南某水果种植基地的水果,公司王总经理与该种植基地的负责人张老板商定一次性采购一种水果的采购价y(千元/吨)与采购量x(吨)之间的函数关系的图象如图中的折线MNP所示(不包含端点M,但包含端点P).
(1)求y与x之间的函数关系式;
(2)已知该水果种植基地种植该水果的成本是8千元/吨,那么王总经理的采购量为多少时,该水果基地在这次买卖中所获得利润W最大?最大利润是多少?
21.已知函数f(x)=2sin(ωx+φ)(,)的图象的相邻两条对称轴之间的距离为4,且有一个零点为.
(1)求函数f(x)的解析式;
(2)若,且,求f(θ+3)的值;
(3)若在上恒成立,求实数m的取值范围.
22.已知函数(a∈R)且函数f(x)是奇函数.
(1)求a的值;
(2)是否存在这样的实数m,使f(3m﹣mcosθ)+f(cosθ﹣6)>f(0)对所有的均成立?若存在,求出适合条件的实数m的值或范围;若不存在,说明理由.
2019-2020学年江西省吉安市高一(上)期末数学试卷
参考答案与试题解析
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【分析】可以求出集合B,然后进行并集的运算即可.
【解答】解:∵A={x|﹣1<x<3},B={x|1<x<2},
∴A∪B=(﹣1,3).
故选:C.
2.【分析】由根式内部的代数式大于等于0,分式的分母不为0联立不等式组求解.
【解答】解:由,解得x≤1且x≠﹣2.
∴函数的定义域为(﹣∞,﹣2)∪(﹣2,1].
故选:D.
3.【分析】利用指数函数、对数函数的性质直接求解.
【解答】解:∵0<<20=1,
b=log23>log22=1,
<=0,
∴a,b,c的大小关系是c<a<b.
故选:B.
4.【分析】由题意利用任意角的三角函数的定义求得y0的值,可得tanα的值,再利用同角三角函数的基本关系,求得要求式子的值.
【解答】解:∵角α的终边与单位圆交于点,∴+=1,∴y0=±,∴tanα==±.
则当tanα=时,==;
当tanα=﹣时,==﹣;
故选:C.
5.【分析】函数f(x)=﹣2x2﹣(2a+1)x+3的对称轴x=﹣,从而﹣,由此能求出a的取值范围.
【解答】解:∵函数f(x)=﹣2x2﹣(2a+1)x+3在区间[2,3]上是增函数,
函数f(x)=﹣2x2﹣(2a+1)x+3的对称轴x=﹣,
∴﹣,
解得a≤﹣.
∴a的取值范围是(﹣∞,﹣].
故选:A.
6.【分析】直接利用角的关系式的变换的应用求出结果.
【解答】解:已知,,
所以:=tan[()﹣()]==.
故选:A.
7.【分析】解题的关键是发现f(x)+f(﹣x)=1,由此得解.
【解答】解:易知函数f(x)在[﹣a,a]上单调,且==,
∴M+N+f(2020)+f(﹣2020)=2.
故选:B.
8.【分析】由函数周期求出ω,由特殊点的坐标求出φ的值,可得f(x)的解析式,从而求得f()的值
【解答】解:∵T=﹣(﹣)=,
∴T=π=?ω=2.
由2×(﹣)+φ=2kπ+π,可得φ=2kπ+π+,
∵﹣π<φ<π,取k=﹣1可得:φ=﹣,
∴f(x)=2cos(2x﹣)
∴=2cos(2×﹣)=2cos=2×(﹣)=﹣1.
故选:C.
9.【分析】根据函数奇偶性和单调性之间的关系,即可得到结论.
【解答】解:由题意可得,奇函数f(x)在(﹣∞,0)上单调递增,根据奇函数的对称性可知f(x)在(0,+∞)上单调递增,
由f(4)=0可得f(﹣4)=0,
因为xf(x)<0,
则或,
解可得,0<x<4或﹣4<x<0.
故不等式的解集(﹣4,0)∪(0,4).
故选:D.
10.【分析】根据条件即可得出=,进行向量的数乘运算,并代入即可.
【解答】解:∵E,F,G分别是AB,DE,CF的中点,且ABCD是正方形,,
∴
=
=
=
=
=
=
=.
故选:D.
11.【分析】确定函数是奇函数,图象关于原点对称,x>0时,f(x)=logax(0<a<1)是单调减函数,即可得出结论.
【解答】解:由题意,f(﹣x)=﹣f(x),所以函数是奇函数,图象关于原点对称,排除B、D;
x>0时,f(x)=logax(0<a<1)是单调减函数,排除A.
故选:C.
12.【分析】本题先根据函数是奇函数及f(x+2)+f(x)=0可得f(x)关于x==1对称,然后将函数g(x)=xf(x)﹣1在区间[﹣6,6]上所有零点个数问题,转化为y=f(x)与y=两个函数图象在区间[﹣6,6]上交点个数问题.再结合图象可得到正确选项.
【解答】解:由题意,f(x)是定义在R上的奇函数,
f(x+2)=﹣f(x)=f(﹣x),则f(x)关于x==1对称,
函数g(x)=xf(x)﹣1在区间[﹣6,6]上所有零点个数问题,
可转化为y=f(x)与y=两个函数图象在区间[﹣6,6]上交点个数问题.
根据题意,可画出图象如下:
根据图象,可知y=f(x)与y=两个函数图象在区间[﹣6,6]上有6个交点.
故函数g(x)=xf(x)﹣1在区间[﹣6,6]上有6个零点.
故选:D.
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.【分析】根据题意,由向量、的模以及夹角计算可得?的值,进而由数量积的计算可得(4﹣)2=(4)2﹣8?+2,代入数据计算,再开方可得答案.
【解答】解:∵||=2,||=3,,的夹角为60°;
∴?=cos60°=2×3×=3;
∴(4﹣)2=(4)2﹣8?+2=16×4﹣24+9=49;
∴|4﹣|=7.
故答案为:7.
14.【分析】由题意利用同角三角函数的基本关系求得sinα的值,再利用诱导公式、二倍角公式,化简所给的式子,可得结果.
【解答】解:∵已知,且,∴sinα==,
则==
====,
故答案为:.
15.【分析】建立坐标系,结合二次函数的性质即可求解.
【解答】解:建立如图坐标系;
则B(0,0),C(2,0)P(x,1);
∴=(x,1),=(x﹣2,1);
∴=x(x﹣2)+1=(x﹣1)2≥0;
故答案为:[0,+∞)
16.【分析】设y=ax2+bx,(a≠0),由当产量为40000辆时,创造的价值达到最大6000万元,得,解得:,从而求出函数解析式,
令y=56250即可解得x的值.
【解答】解:设y=ax2+bx,(a≠0),
∵当产量为40000辆时,创造的价值达到最大6000万元,
∴,解得:,
∴,
令y=56250得:,
解得:x=30000或50000,
故答案为:30000或50000.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.【分析】(1)求出a=1时集合B,再求?UB,化简集合A,求出A∩(?UB);
(2)化简集合C和B,根据C?B列不等式求出a的取值范围.
【解答】解:(1)当a=1时,B={x|1+x≤0}={x|x≤﹣1},
则?UB={x|x>﹣1}.
又A={x|3x≤9}={x|x≤2},
所以A∩(?UB)={x|﹣1<x≤2};
(2)由C={x|0<log2x≤2}={x|1<x≤4},
B={x|a+x≤0}={x|x≤﹣a},
因为C?B,所以﹣a≥4,
解得a≤﹣4.
所以实数a的取值范围是(﹣∞,﹣4].
18.【分析】(1)首先利用三角函数关系式的变换,把函数的关系式变形成正弦型函数,进一步求出函数的最小正周期.
(2)利用函数的性质的应用求出结果.
【解答】解:(1)函数=2cosx(sinx)﹣==sin(2x+).
所以函数的最小正周期为.
(2)由(k∈Z),
整理得:(k∈Z),
所以f(x)的单调递减区间是[](k∈Z).
当时,.
则.
故f(x)在区间为[]上的最小值是﹣1,最大值是0.
19.【分析】(1)用赋值法令y=,得f(1)=f(x)﹣f(x)=0,令x=1,y=﹣1,可得f(﹣1)=0,令y=﹣1,可得f(﹣x)=f(x)﹣f(﹣1)=f(x),可得函数f(x)是偶函数.
(2)f(2﹣)﹣f()=f()=f(2x﹣4),所以不等式可变为f(2x﹣4)≤f(2),
【解答】解:(1)令y=,则f(x?)=f(x)﹣f(),
得f(1)=f(x)﹣f(x)=0,
再令x=1,y=﹣1,可得f(﹣1)=f(1)﹣f(﹣1),
得2f(﹣1)=f(1)=0,
所以f(﹣1)=0,
令y=﹣1,可得f(﹣x)=f(x)﹣f(﹣1)=f(x),
所以f(x)是偶函数.
(2)因为f(2)=1,所以f(﹣2)=1.
因为函数f(x)在(﹣∞,0)上是减函数,且是偶函数,
所以函数f(x)在(0,+∞)上是增函数.
又f(2﹣)﹣f()=f()=f(2x﹣4),
所以f(2x﹣4)≤f(2),
等价于或,
解得1<x≤3或1≤x<2.
所以不等式f(2﹣)﹣f()≤1的解集为[1,2)∪(2,3].
20.【分析】(1)利用待定系数法分段即可求出y与x之间的函数关系式;
(2)分段求出最大值,再比较即可.
【解答】解:(1)当0<x≤8时,y=16;
当8≤x≤16时,设NP满足的函数关系式为y=kx+b,
则,解得;
所以,
综上,;
(2)当0<x≤8 时,该水果种植基地获得的利润W=(16﹣8)x=8x≤64,此时该水果种植基地获得的最大利润为64千元;
当8<x≤16时,该水果种植基地获得的利润为W=(﹣﹣8)x=﹣=﹣,
所以当x=12 时,利润W取得最大值,最大值为72千元.
因为72千元>64千元,
所以当王总经理采购量为12吨时,该水果种植基地在这次买卖中所获得的利润最大,最大利润为72千元.
21.【分析】(1)由对称轴之间的距离求出ω代入零点求出φ;
(2)先由,求得sin(θ+)=,进而得cos(θ+)==.再结合f(θ+3)=2sin[(θ+3)+]=2sin[(θ+)+]展开即可求解;
(3)先由,x+∈[﹣,],求出f(x)min=2sin(﹣)=﹣1,进而求得结论
【解答】解:(1)因为函数f(x)图象的相邻两条对称轴之间的距离为4,
所以函数f(x)的最小正周期是8.
所以=8,解得ω=.
所以f(x)=2sin(x+φ).
因为函数f(x)有一个零点﹣,
所以f(x)=2sin[×)+φ]=0,得﹣+φ=kπ(k∈Z).
解得φ=kπ(k∈Z).
由知,φ=,
所以f(x)=2sin(x+)
(2)由,得2sin(θ+)=,
即sin(θ+)=,
由,得θ+∈(﹣,),
所以cos(θ+)==.
所以f(θ+3)=2sin[(θ+3)+]
=2sin[(θ+)+]
=2sin(θ+)cos+2cos(θ+)sin
=2××(﹣)+2××
=﹣;
(3)由,x+∈[﹣,],
所以当时,
f(x)min=2sin(﹣)=﹣1,
若在上恒成立;
则f(x)min>,即﹣1,解得m<0.
故实数m的取值范围为(﹣∞,0).
22.【分析】(1)由奇函数的定义可得f(0)=0,可得a的值,检验可得所求;
(2)由f(x)的奇偶性和单调性,消去f,可得3m﹣mcosθ>6﹣cosθ,方法一、运用分类讨论思想,结合余弦函数的性质,解不等式可得所求范围;
方法二、运用参数分离,结合余弦函数的性质,可得所求范围.
【解答】解:(1)函数(a∈R)的定义域是R,
因为函数f(x)是奇函数,所以f(0)=0.
即a+1=0,解得a=﹣1,f(x)=(ex﹣e﹣x),
f(﹣x)+f(x)=(e﹣x﹣ex)+(ex﹣e﹣x)=0,即f(﹣x)=﹣f(x),
可得f(x)为奇函数,故a=﹣1;
(2)因为f(x)是定义在R上的奇函数,
因为f(3m﹣mcosθ)+f(cosθ﹣6)>f(0)=0,
所以f(3m﹣mcosθ)>﹣f(cosθ﹣6),
得f(3m﹣mcosθ)>f(6﹣cosθ),
因为f(x)在[0,+∞)上是增函数,且f(x)为奇函数,
所以f(x)在R上也为增函数,
所以3m﹣mcosθ>6﹣cosθ,
解法1:即(m﹣1)cosθ<3m﹣6,
因为,所以cosθ∈[0,1].
当m﹣1>0,即m>1时,cosθ<对所有的均成立,
需满足1<,则m﹣1<3m﹣6,解得m>;
当m﹣1<0,即m<1时,cosθ>对所有的均成立,
需满足0>,则3m﹣6>0,
解得m>2,不满足前提条件,舍去;
当m﹣1=0,即m=1时,不等式(m﹣1)cosθ<3m﹣6可化为0<﹣3不成立,故舍去.
综上,存在这一的实数m,使f(3m﹣mcosθ)+f(cosθ﹣6)>f(0)对所有的均成立,
适合条件的实数m的取值范围是(,+∞).
解法2:即m(3﹣cosθ)>6﹣cosθ,
因为,所以cosθ∈[0,1].,
即3﹣cosθ>0,所以m>=1+,
所以当cosθ=1时,1+取得最大值,
所以要使f(3m﹣mcosθ)+f(cosθ﹣6)>f(0)对所有的均成立,
实数m的取值范围是(,+∞)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)已知A={x|﹣1<x<3},B={x|0<x﹣1<1},则A∪B=( )
A.(﹣∞,+∞) B.(1,2) C.(﹣1,3) D.(1,3)
2.(5分)函数的定义域为( )
A.(﹣2,1] B.(﹣∞,﹣2)∪(﹣2,1)
C.(﹣2,1) D.(﹣∞,﹣2)∪(﹣2,1]
3.(5分)设,b=log23,,则a,b,c的大小关系是( )
A.a<c<b B.c<a<b C.b<c<a D.c<b<a
4.(5分)已知角α的终边与单位圆交于点,则=( )
A. B.或 C.或 D.
5.(5分)函数f(x)=﹣2x2﹣(2a+1)x+3在区间[2,3]上是增函数,则a的取值范围是( )
A. B. C. D.
6.(5分)已知,,则=( )
A.1 B.2 C. D.
7.(5分)已知a>0,设函数(x∈[﹣a,a])的最大值为M,最小值为N,那么M+N+f(2020)+f(﹣2020)=( )
A.1 B.2 C.3 D.4
8.(5分)函数f(x)=2cos(ωx+φ)(ω>0,|φ|<π)的部分图象如图所示,则=( )
A. B. C.﹣1 D.1
9.(5分)定义在R上的奇函数f(x),对任意的x1,x2∈(﹣∞,0),都有,且.f(4)=0.,则不等式xf(x)<0的解集是( )
A.(﹣∞,﹣4)∪(4,+∞) B.(﹣4,0)∪(4,+∞)
C.(﹣∞,﹣4)∪(0,4) D.(﹣4,0)∪(0,4)
10.(5分)在正方形ABCD中,设=,AD=,已知E,F,G分别是AB,DE,CF的中点,则=( )
A. B. C. D.
11.(5分)函数f(x)=(0<a<1)图象的大致形状是( )
A. B.
C. D.
12.(5分)已知f(x)是定义在R上的奇函数,且满足f(x+2)+f(x)=0,当x∈[0,1]时,f(x)=x2,则函数g(x)=xf(x)﹣1在区间[﹣6,6]上所有零点的个数为( )
A.0 B.2 C.4 D.6
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.(5分)已知||=2,||=3,,的夹角为60°,则|4﹣|= .
14.(5分)已知,且,则的值为 .
15.(5分)在矩形ABCD中,AB=1,BC=2,P是直线AD上的动点(端点可取),则的取值范围是 .
16.(5分)新能源汽车包括纯电动汽车、增程式电动汽车、混合动力汽车、燃料电池电动汽车、氢发动机汽车、其他新能源汽车等.它是未来汽车的发展方向.一个新能源汽车制造厂引进了一条新能源汽车整车装配流水线,这条流水线生产的新能源汽车数量x(辆)与创造的价值y(万元)之间满足二次函数关系.已知产量为0时,创造的价值也为0;当产量为40000辆时,创造的价值达到最大6000万元.若这家工厂希望利用这条流水线创收达到56250万元,则它可能生产的新能源汽车数量是 辆.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知全集U=R,A={x|3x≤9},B={x|a+x≤0},C={x|0<log2x≤2}.
(1)当a=1时,求A∩(?UB);
(2)若C?B,求实数a的取值范围.
18.已知函数.
(1)求f(x)的最小正周期;
(2)求f(x)的单调递减区间以及在区间上的最值.
19.定义在(﹣∞,0)∪(0,+∞)上的函数y=f(x)满足,且函数f(x)在(﹣∞,0)上是减函数.
(1)求f(﹣1),并证明函数y=f(x)是偶函数;
(2)若f(2)=1,解不等式.
20.第七届世界军人运动会(7thCISMMilitaryWorldGames),简称“武汉军运会”,于2019年10月18日至27日在中国武汉举行,共设置射击、游泳、田径篮球等27个大项、329个小项.来自100多个国家的近万名现役军人同台竞技.会议期间,某公司欲采购海南某水果种植基地的水果,公司王总经理与该种植基地的负责人张老板商定一次性采购一种水果的采购价y(千元/吨)与采购量x(吨)之间的函数关系的图象如图中的折线MNP所示(不包含端点M,但包含端点P).
(1)求y与x之间的函数关系式;
(2)已知该水果种植基地种植该水果的成本是8千元/吨,那么王总经理的采购量为多少时,该水果基地在这次买卖中所获得利润W最大?最大利润是多少?
21.已知函数f(x)=2sin(ωx+φ)(,)的图象的相邻两条对称轴之间的距离为4,且有一个零点为.
(1)求函数f(x)的解析式;
(2)若,且,求f(θ+3)的值;
(3)若在上恒成立,求实数m的取值范围.
22.已知函数(a∈R)且函数f(x)是奇函数.
(1)求a的值;
(2)是否存在这样的实数m,使f(3m﹣mcosθ)+f(cosθ﹣6)>f(0)对所有的均成立?若存在,求出适合条件的实数m的值或范围;若不存在,说明理由.
2019-2020学年江西省吉安市高一(上)期末数学试卷
参考答案与试题解析
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【分析】可以求出集合B,然后进行并集的运算即可.
【解答】解:∵A={x|﹣1<x<3},B={x|1<x<2},
∴A∪B=(﹣1,3).
故选:C.
2.【分析】由根式内部的代数式大于等于0,分式的分母不为0联立不等式组求解.
【解答】解:由,解得x≤1且x≠﹣2.
∴函数的定义域为(﹣∞,﹣2)∪(﹣2,1].
故选:D.
3.【分析】利用指数函数、对数函数的性质直接求解.
【解答】解:∵0<<20=1,
b=log23>log22=1,
<=0,
∴a,b,c的大小关系是c<a<b.
故选:B.
4.【分析】由题意利用任意角的三角函数的定义求得y0的值,可得tanα的值,再利用同角三角函数的基本关系,求得要求式子的值.
【解答】解:∵角α的终边与单位圆交于点,∴+=1,∴y0=±,∴tanα==±.
则当tanα=时,==;
当tanα=﹣时,==﹣;
故选:C.
5.【分析】函数f(x)=﹣2x2﹣(2a+1)x+3的对称轴x=﹣,从而﹣,由此能求出a的取值范围.
【解答】解:∵函数f(x)=﹣2x2﹣(2a+1)x+3在区间[2,3]上是增函数,
函数f(x)=﹣2x2﹣(2a+1)x+3的对称轴x=﹣,
∴﹣,
解得a≤﹣.
∴a的取值范围是(﹣∞,﹣].
故选:A.
6.【分析】直接利用角的关系式的变换的应用求出结果.
【解答】解:已知,,
所以:=tan[()﹣()]==.
故选:A.
7.【分析】解题的关键是发现f(x)+f(﹣x)=1,由此得解.
【解答】解:易知函数f(x)在[﹣a,a]上单调,且==,
∴M+N+f(2020)+f(﹣2020)=2.
故选:B.
8.【分析】由函数周期求出ω,由特殊点的坐标求出φ的值,可得f(x)的解析式,从而求得f()的值
【解答】解:∵T=﹣(﹣)=,
∴T=π=?ω=2.
由2×(﹣)+φ=2kπ+π,可得φ=2kπ+π+,
∵﹣π<φ<π,取k=﹣1可得:φ=﹣,
∴f(x)=2cos(2x﹣)
∴=2cos(2×﹣)=2cos=2×(﹣)=﹣1.
故选:C.
9.【分析】根据函数奇偶性和单调性之间的关系,即可得到结论.
【解答】解:由题意可得,奇函数f(x)在(﹣∞,0)上单调递增,根据奇函数的对称性可知f(x)在(0,+∞)上单调递增,
由f(4)=0可得f(﹣4)=0,
因为xf(x)<0,
则或,
解可得,0<x<4或﹣4<x<0.
故不等式的解集(﹣4,0)∪(0,4).
故选:D.
10.【分析】根据条件即可得出=,进行向量的数乘运算,并代入即可.
【解答】解:∵E,F,G分别是AB,DE,CF的中点,且ABCD是正方形,,
∴
=
=
=
=
=
=
=.
故选:D.
11.【分析】确定函数是奇函数,图象关于原点对称,x>0时,f(x)=logax(0<a<1)是单调减函数,即可得出结论.
【解答】解:由题意,f(﹣x)=﹣f(x),所以函数是奇函数,图象关于原点对称,排除B、D;
x>0时,f(x)=logax(0<a<1)是单调减函数,排除A.
故选:C.
12.【分析】本题先根据函数是奇函数及f(x+2)+f(x)=0可得f(x)关于x==1对称,然后将函数g(x)=xf(x)﹣1在区间[﹣6,6]上所有零点个数问题,转化为y=f(x)与y=两个函数图象在区间[﹣6,6]上交点个数问题.再结合图象可得到正确选项.
【解答】解:由题意,f(x)是定义在R上的奇函数,
f(x+2)=﹣f(x)=f(﹣x),则f(x)关于x==1对称,
函数g(x)=xf(x)﹣1在区间[﹣6,6]上所有零点个数问题,
可转化为y=f(x)与y=两个函数图象在区间[﹣6,6]上交点个数问题.
根据题意,可画出图象如下:
根据图象,可知y=f(x)与y=两个函数图象在区间[﹣6,6]上有6个交点.
故函数g(x)=xf(x)﹣1在区间[﹣6,6]上有6个零点.
故选:D.
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.【分析】根据题意,由向量、的模以及夹角计算可得?的值,进而由数量积的计算可得(4﹣)2=(4)2﹣8?+2,代入数据计算,再开方可得答案.
【解答】解:∵||=2,||=3,,的夹角为60°;
∴?=cos60°=2×3×=3;
∴(4﹣)2=(4)2﹣8?+2=16×4﹣24+9=49;
∴|4﹣|=7.
故答案为:7.
14.【分析】由题意利用同角三角函数的基本关系求得sinα的值,再利用诱导公式、二倍角公式,化简所给的式子,可得结果.
【解答】解:∵已知,且,∴sinα==,
则==
====,
故答案为:.
15.【分析】建立坐标系,结合二次函数的性质即可求解.
【解答】解:建立如图坐标系;
则B(0,0),C(2,0)P(x,1);
∴=(x,1),=(x﹣2,1);
∴=x(x﹣2)+1=(x﹣1)2≥0;
故答案为:[0,+∞)
16.【分析】设y=ax2+bx,(a≠0),由当产量为40000辆时,创造的价值达到最大6000万元,得,解得:,从而求出函数解析式,
令y=56250即可解得x的值.
【解答】解:设y=ax2+bx,(a≠0),
∵当产量为40000辆时,创造的价值达到最大6000万元,
∴,解得:,
∴,
令y=56250得:,
解得:x=30000或50000,
故答案为:30000或50000.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.【分析】(1)求出a=1时集合B,再求?UB,化简集合A,求出A∩(?UB);
(2)化简集合C和B,根据C?B列不等式求出a的取值范围.
【解答】解:(1)当a=1时,B={x|1+x≤0}={x|x≤﹣1},
则?UB={x|x>﹣1}.
又A={x|3x≤9}={x|x≤2},
所以A∩(?UB)={x|﹣1<x≤2};
(2)由C={x|0<log2x≤2}={x|1<x≤4},
B={x|a+x≤0}={x|x≤﹣a},
因为C?B,所以﹣a≥4,
解得a≤﹣4.
所以实数a的取值范围是(﹣∞,﹣4].
18.【分析】(1)首先利用三角函数关系式的变换,把函数的关系式变形成正弦型函数,进一步求出函数的最小正周期.
(2)利用函数的性质的应用求出结果.
【解答】解:(1)函数=2cosx(sinx)﹣==sin(2x+).
所以函数的最小正周期为.
(2)由(k∈Z),
整理得:(k∈Z),
所以f(x)的单调递减区间是[](k∈Z).
当时,.
则.
故f(x)在区间为[]上的最小值是﹣1,最大值是0.
19.【分析】(1)用赋值法令y=,得f(1)=f(x)﹣f(x)=0,令x=1,y=﹣1,可得f(﹣1)=0,令y=﹣1,可得f(﹣x)=f(x)﹣f(﹣1)=f(x),可得函数f(x)是偶函数.
(2)f(2﹣)﹣f()=f()=f(2x﹣4),所以不等式可变为f(2x﹣4)≤f(2),
【解答】解:(1)令y=,则f(x?)=f(x)﹣f(),
得f(1)=f(x)﹣f(x)=0,
再令x=1,y=﹣1,可得f(﹣1)=f(1)﹣f(﹣1),
得2f(﹣1)=f(1)=0,
所以f(﹣1)=0,
令y=﹣1,可得f(﹣x)=f(x)﹣f(﹣1)=f(x),
所以f(x)是偶函数.
(2)因为f(2)=1,所以f(﹣2)=1.
因为函数f(x)在(﹣∞,0)上是减函数,且是偶函数,
所以函数f(x)在(0,+∞)上是增函数.
又f(2﹣)﹣f()=f()=f(2x﹣4),
所以f(2x﹣4)≤f(2),
等价于或,
解得1<x≤3或1≤x<2.
所以不等式f(2﹣)﹣f()≤1的解集为[1,2)∪(2,3].
20.【分析】(1)利用待定系数法分段即可求出y与x之间的函数关系式;
(2)分段求出最大值,再比较即可.
【解答】解:(1)当0<x≤8时,y=16;
当8≤x≤16时,设NP满足的函数关系式为y=kx+b,
则,解得;
所以,
综上,;
(2)当0<x≤8 时,该水果种植基地获得的利润W=(16﹣8)x=8x≤64,此时该水果种植基地获得的最大利润为64千元;
当8<x≤16时,该水果种植基地获得的利润为W=(﹣﹣8)x=﹣=﹣,
所以当x=12 时,利润W取得最大值,最大值为72千元.
因为72千元>64千元,
所以当王总经理采购量为12吨时,该水果种植基地在这次买卖中所获得的利润最大,最大利润为72千元.
21.【分析】(1)由对称轴之间的距离求出ω代入零点求出φ;
(2)先由,求得sin(θ+)=,进而得cos(θ+)==.再结合f(θ+3)=2sin[(θ+3)+]=2sin[(θ+)+]展开即可求解;
(3)先由,x+∈[﹣,],求出f(x)min=2sin(﹣)=﹣1,进而求得结论
【解答】解:(1)因为函数f(x)图象的相邻两条对称轴之间的距离为4,
所以函数f(x)的最小正周期是8.
所以=8,解得ω=.
所以f(x)=2sin(x+φ).
因为函数f(x)有一个零点﹣,
所以f(x)=2sin[×)+φ]=0,得﹣+φ=kπ(k∈Z).
解得φ=kπ(k∈Z).
由知,φ=,
所以f(x)=2sin(x+)
(2)由,得2sin(θ+)=,
即sin(θ+)=,
由,得θ+∈(﹣,),
所以cos(θ+)==.
所以f(θ+3)=2sin[(θ+3)+]
=2sin[(θ+)+]
=2sin(θ+)cos+2cos(θ+)sin
=2××(﹣)+2××
=﹣;
(3)由,x+∈[﹣,],
所以当时,
f(x)min=2sin(﹣)=﹣1,
若在上恒成立;
则f(x)min>,即﹣1,解得m<0.
故实数m的取值范围为(﹣∞,0).
22.【分析】(1)由奇函数的定义可得f(0)=0,可得a的值,检验可得所求;
(2)由f(x)的奇偶性和单调性,消去f,可得3m﹣mcosθ>6﹣cosθ,方法一、运用分类讨论思想,结合余弦函数的性质,解不等式可得所求范围;
方法二、运用参数分离,结合余弦函数的性质,可得所求范围.
【解答】解:(1)函数(a∈R)的定义域是R,
因为函数f(x)是奇函数,所以f(0)=0.
即a+1=0,解得a=﹣1,f(x)=(ex﹣e﹣x),
f(﹣x)+f(x)=(e﹣x﹣ex)+(ex﹣e﹣x)=0,即f(﹣x)=﹣f(x),
可得f(x)为奇函数,故a=﹣1;
(2)因为f(x)是定义在R上的奇函数,
因为f(3m﹣mcosθ)+f(cosθ﹣6)>f(0)=0,
所以f(3m﹣mcosθ)>﹣f(cosθ﹣6),
得f(3m﹣mcosθ)>f(6﹣cosθ),
因为f(x)在[0,+∞)上是增函数,且f(x)为奇函数,
所以f(x)在R上也为增函数,
所以3m﹣mcosθ>6﹣cosθ,
解法1:即(m﹣1)cosθ<3m﹣6,
因为,所以cosθ∈[0,1].
当m﹣1>0,即m>1时,cosθ<对所有的均成立,
需满足1<,则m﹣1<3m﹣6,解得m>;
当m﹣1<0,即m<1时,cosθ>对所有的均成立,
需满足0>,则3m﹣6>0,
解得m>2,不满足前提条件,舍去;
当m﹣1=0,即m=1时,不等式(m﹣1)cosθ<3m﹣6可化为0<﹣3不成立,故舍去.
综上,存在这一的实数m,使f(3m﹣mcosθ)+f(cosθ﹣6)>f(0)对所有的均成立,
适合条件的实数m的取值范围是(,+∞).
解法2:即m(3﹣cosθ)>6﹣cosθ,
因为,所以cosθ∈[0,1].,
即3﹣cosθ>0,所以m>=1+,
所以当cosθ=1时,1+取得最大值,
所以要使f(3m﹣mcosθ)+f(cosθ﹣6)>f(0)对所有的均成立,
实数m的取值范围是(,+∞)
同课章节目录
