人教版九年级数学下册27.2.2:相似三角形的性质及应用 学案(无答案)
文档属性
| 名称 | 人教版九年级数学下册27.2.2:相似三角形的性质及应用 学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 903.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 07:39:27 | ||
图片预览


文档简介
相似三角形的性质及应用
课前自主复习
1.相似三角形的性质
已知两个相似三角形的相似比为,则对应高的比为 ,对应中线的比为 ,对应角平分线的比为 ,周长的比为 ,面积的比为 .
2.相似多边形的周长比等于 ,相似多边形的面积比等于相似比的 .
3.已知D、E、F分别是△ABC三边的中点,若△ABC的周长为cm,则△DEF的周长为
Cm;若△ABC的面积为cm?,则△DEF的面积为 cm?
4.双直角三角形(射影定理)
如图,在Rt△ABC中,已知∠BAC=90°,AD⊥BC,则
由Rt△ABD∽Rt△CAD可得 ;
由Rt△ABD∽Rt△CBA可得 ;
由Rt△CAD∽Rt△CBA可得 ;
5.如果两个图形不仅是相似图形,而且每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做 .这个点叫 ,这时的相似比又称为 .
课前基础自测
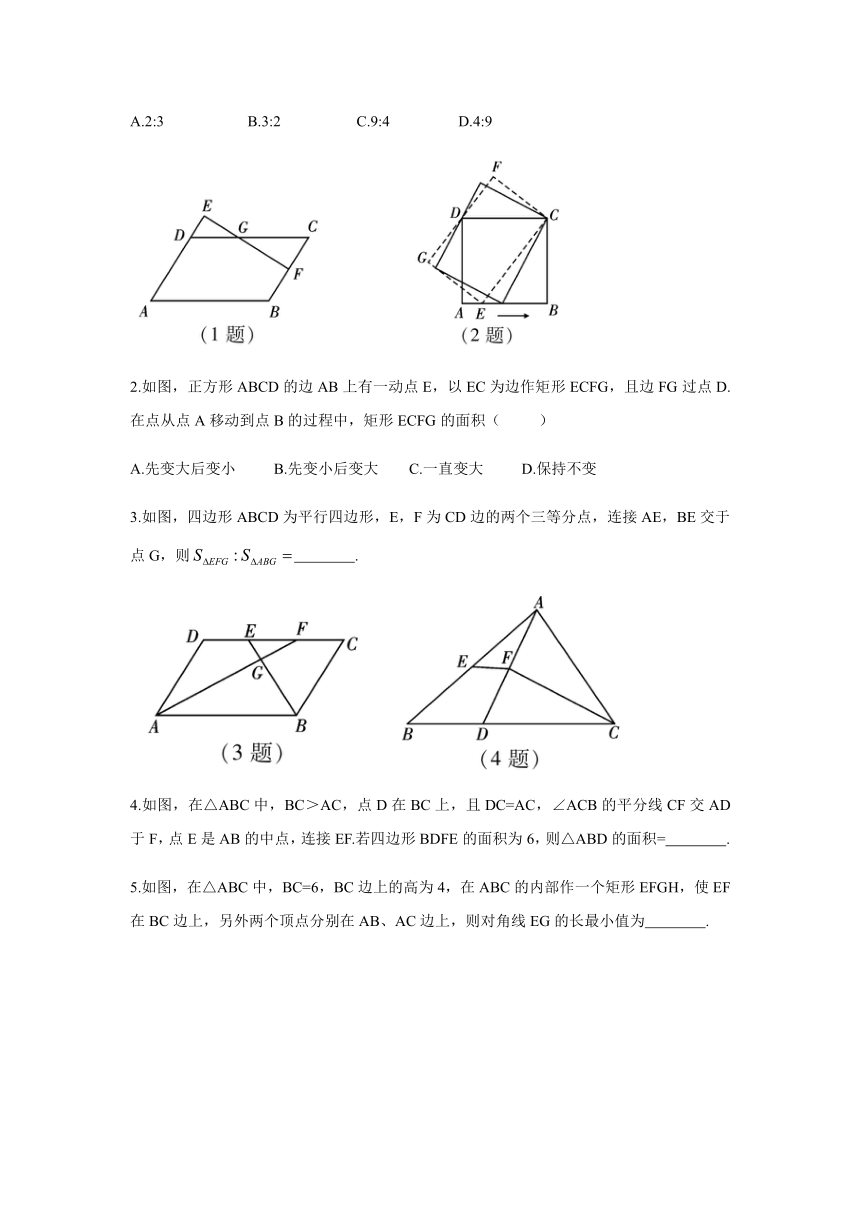
1.如图□ABCD,F为BC中点,延长AD至点E,使DE:AD=1:3,连接EF交DC于点G,则( )
A.2:3 B.3:2 C.9:4 D.4:9
2.如图,正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D.在点从点A移动到点B的过程中,矩形ECFG的面积( )
A.先变大后变小 B.先变小后变大 C.一直变大 D.保持不变
3.如图,四边形ABCD为平行四边形,E,F为CD边的两个三等分点,连接AE,BE交于点G,则 .
4.如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF.若四边形BDFE的面积为6,则△ABD的面积= .
5.如图,在△ABC中,BC=6,BC边上的高为4,在ABC的内部作一个矩形EFGH,使EF在BC边上,另外两个顶点分别在AB、AC边上,则对角线EG的长最小值为 .
课堂讲练结合
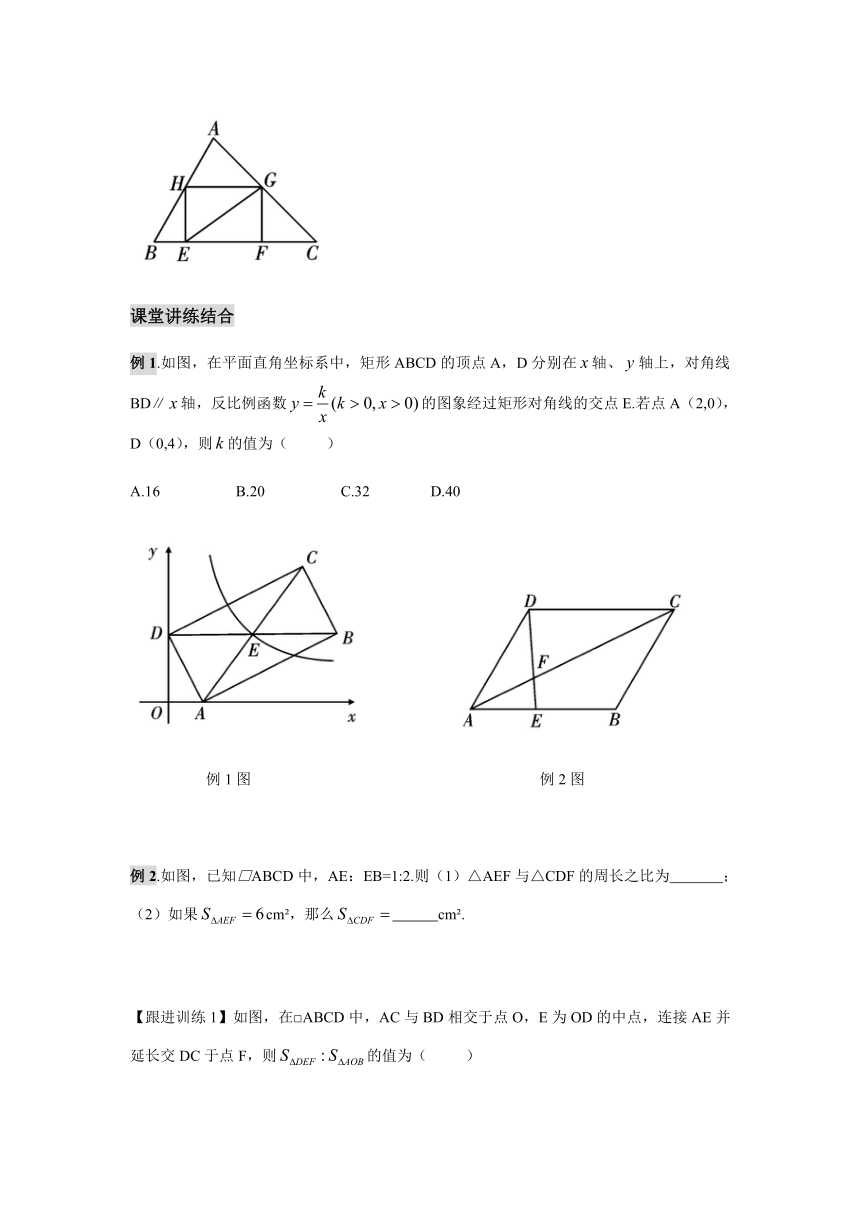
例1.如图,在平面直角坐标系中,矩形ABCD的顶点A,D分别在轴、轴上,对角线BD∥轴,反比例函数的图象经过矩形对角线的交点E.若点A(2,0),D(0,4),则的值为( )
A.16 B.20 C.32 D.40
例1图 例2图
例2.如图,已知□ABCD中,AE:EB=1:2.则(1)△AEF与△CDF的周长之比为 ;(2)如果cm?,那么 cm?.
【跟进训练1】如图,在□ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则的值为( )
A.1:3 B.1:5 C.1:6 D.1:11
【跟进训练2】如图,矩形ABCD中,AB=4,AD=6,点E为AD中点,点P为线段AB上一个动点,连接EP,将△APE沿PE折叠得到△FPE,连接CE,CF,当△ECF为直角三角形时,AP的长为 .
例3.如图,矩形ABCD中,AB=a,BC=b,点M,N分别在边AB,CD上,点E,F分别在BC,AD上,MN,EF交于点P,记若的值为3,当点N是矩形的顶点且∠MPE=60°,MP=EF=3PE时,求a:b的值.
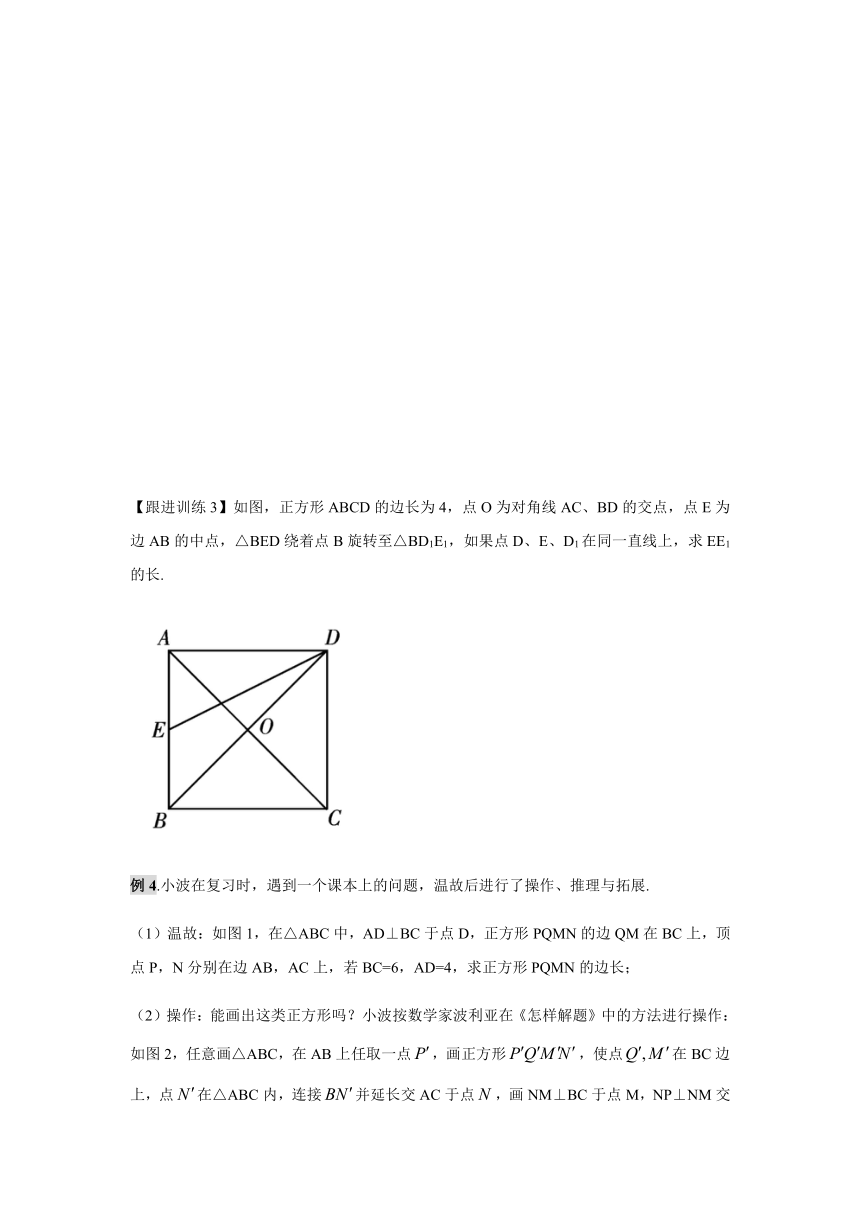
【跟进训练3】如图,正方形ABCD的边长为4,点O为对角线AC、BD的交点,点E为边AB的中点,△BED绕着点B旋转至△BD1E1,如果点D、E、D1在同一直线上,求EE1的长.
例4.小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
(1)温故:如图1,在△ABC中,AD⊥BC于点D,正方形PQMN的边QM在BC上,顶点P,N分别在边AB,AC上,若BC=6,AD=4,求正方形PQMN的边长;
(2)操作:能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作:如图2,任意画△ABC,在AB上任取一点,画正方形,使点在BC边上,点在△ABC内,连接并延长交AC于点,画NM⊥BC于点M,NP⊥NM交AB于点P,PQ⊥BC于点Q,得到四边形PQMN.小波把线段BN称为“波利亚线”
(3)推理:证明图2中的四边形PQMN是正方形;
(4)拓展:在(2)的条件下,在射线BN上截取NE=NM,连接EQ,EM(如图3).当tan∠NBM=时,猜想∠QEM的度数,并尝试证明.请帮助小波解决“温故”、“推理”、“拓展”中的问题
课内巩固训练
1.如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE于点F,则BF的长为( )
A. B. C. D.
2.如图,以点O为位似中心,将△ABC放大得到△DEF.若AD=OA,则△ABC与△DEF的面积之比为( )
A.1:2 B.1:4 C.1:5 D.1:6
3.七巧板是我国祖先的一项卓越创造,被誉为“东方魔板”.由边长为的正方形ABCD可以制作一副如图1所示的七巧板,现将这副七巧板在正方形EFGH内拼成如图2所示的“拼搏兔”造型(其中点Q、R分别与图2中的点E、G重合,点P在边EH上),则“拼搏兔”所在正方形EFGH的边长是 .
4.如图,在△ABC中,已知AB=AC=4,BC=6,P是BC边上的一动点(P不与B、C重合),连接AP,∠B=∠APE,边PE与AC交于点D,当△APD为等腰三角形时,则PB之长为 ;
5.如图,Rt△ABM和Rt△ADN的斜边分别为正方形的边AB和AD,其中AM=AN.
(1)求证:Rt△ABM≌Rt△AND;
(2)若MN与AD相交于点T,且,求tan∠ABM的值;
课后作业
A组(基础训练)
1.如图,已知D、E分别是△ABC的AB、AC边上的点,DE∥BC,且,那么AE:AC等于( )
A.1:9 B.1:3 C.1:8 D.1:2
2.如图,在边长为1的正方形ABCD中,已知点E在CB的延长线上,连接ED交AB于点F,,则线面函数图象中,大致能反映与之间函数关系是( )
3.两个相似三角形的最短边分别为5cm和3cm,它们的周长之差为12cm,那么大三角形的周长为( )
A.14cm B.16cm C.18cm D.30cm
4.如图,四边形ABCD与四边形EFGH位似,位似中心是点O,,则 ;
5.如图,在△ABC中,已知D、E分别是AB和AC的中点,F是BC延长线上一点,DF平分CE于点G,CF=1,则BC= ,△ADE与△ABC的周长之比为 ,△CFG与△DFB的面积之比为 .
6.如图,取一张长为a,宽为b的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的a、b应满足的条件是( )
A. B. C. D.
7.如图,已知CD是Rt△ABC的斜边AB上的高,∠BAC的平分线分别交BC、CD于点E、F.成立吗?请说明理由.
8.定义:在△ABC中,点D,E,F分别是边AB,BC,CA上的动点,若△DEF∽△ABC(点D、E、F的对应点分别为点A、B、C),则称△DEF是△ABC的子三角形,如图.
(1)已知:如图1,△ABC是等边三角形,点D,E,F分别是边AB,BC,CA上的动点,且AD=BE=CF.求证:△DEF是△ABC的子三角形.
(2)已知:如图2,△DEF是△ABC的子三角形,且AB=AC,∠A=90°,若BE=,求CF和AD的长.
9.如图,Rt△ABC中,∠ACB=90°,AB=15,BC=9,在线段AB上取一点D,作DF⊥AB交AC于点F,现将△ADF沿DF折叠,使点A落在线段DB上,对应点记为,AD原中点E的对应点记为E1,若△E1FA1∽△E1BF,求AD的长
B组(能力提高)
10.如图,四边形ABCD中,AB=4,BC=6,AB⊥BC,BC⊥CD,E为AD中点,F为BE上的点,且FE=BE,则点F到边CD的距离是 .
11.如图,△ABC是等边三角形,,点D是边BC上一点,连接BH、CH,当∠BHD=60°,∠AHC=90°时,DH= .
12.已知四边形ABCD的一组对边AD、BC的延长线相交于点E.(1)如图(1),若∠ABC=∠ADC=90°,求证:;(2)如图(2),若∠ABC=120°,cos∠ADC=,CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;(3)如图(3),另一组对边AB,DC的延长线相交于点F,若cos∠ABC=cos∠ADC=,CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示).
13.如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC,BC的延长线相交,交点分别为点E、F,DF与AC相交于点M,DE与BC交于点N.(1)如图(1),若CE=CF,求证:DE=DF;(2)如图(2),在∠EDF绕点D旋转的过程中;①探究三条线段AB、CE、CF之间的数量关系,并说明理由;②若CE=4,CF=2,求DN的长.
14.如图,Rt△AOB∽Rt△DOC,∠ABO=30°,∠AOB=∠COD=90°,M为OA的中点,OA=6,将△COD绕点O旋转一周,直线AD,CB交于点P,连接MP,则MP的最小值是
.
15.在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点M从点B出发,在BA边上以每秒3cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B匀速运动,运动时间为t秒(),连接MN.
(1)若△BMN与△ABC相似,求t的值;(2)如图(2),连接AN,CM,若AN⊥CM,求t的值.
