2.3 平行线的性质课课练(含答案)

北师大版数学七年级下册﹒同步课时训练
第二章　相交线与平行线
3　平行线的性质
一、选择题
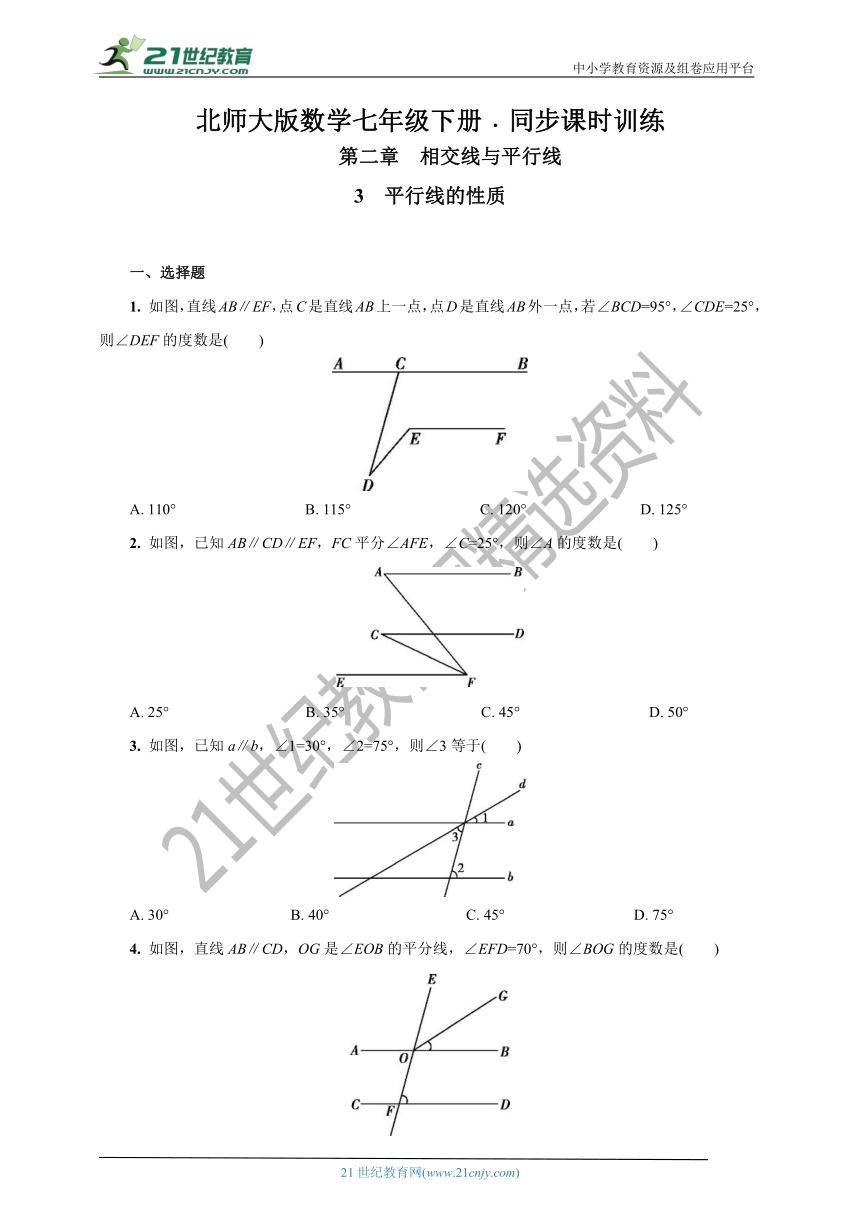
1. 如图，直线AB∥EF，点C是直线AB上一点，点D是直线AB外一点，若∠BCD=95°，∠CDE=25°，则∠DEF的度数是(　　)
A. 110°　　　 B. 115°　　　 C. 120°　　　 D. 125°
2. 如图，已知AB∥CD∥EF，FC平分∠AFE，∠C=25°，则∠A的度数是(　　)
A. 25°　　　 B. 35°　　　 C. 45°　　　 D. 50°
3. 如图，已知a∥b，∠1=30°，∠2=75°，则∠3等于(　　)
A. 30°　　　 B. 40°　　　 C. 45°　　　 D. 75°
4. 如图，直线AB∥CD，OG是∠EOB的平分线，∠EFD=70°，则∠BOG的度数是(　　)
A. 70°　　　 B. 20°　　　 C. 35°　　　 D. 40°
二、填空题
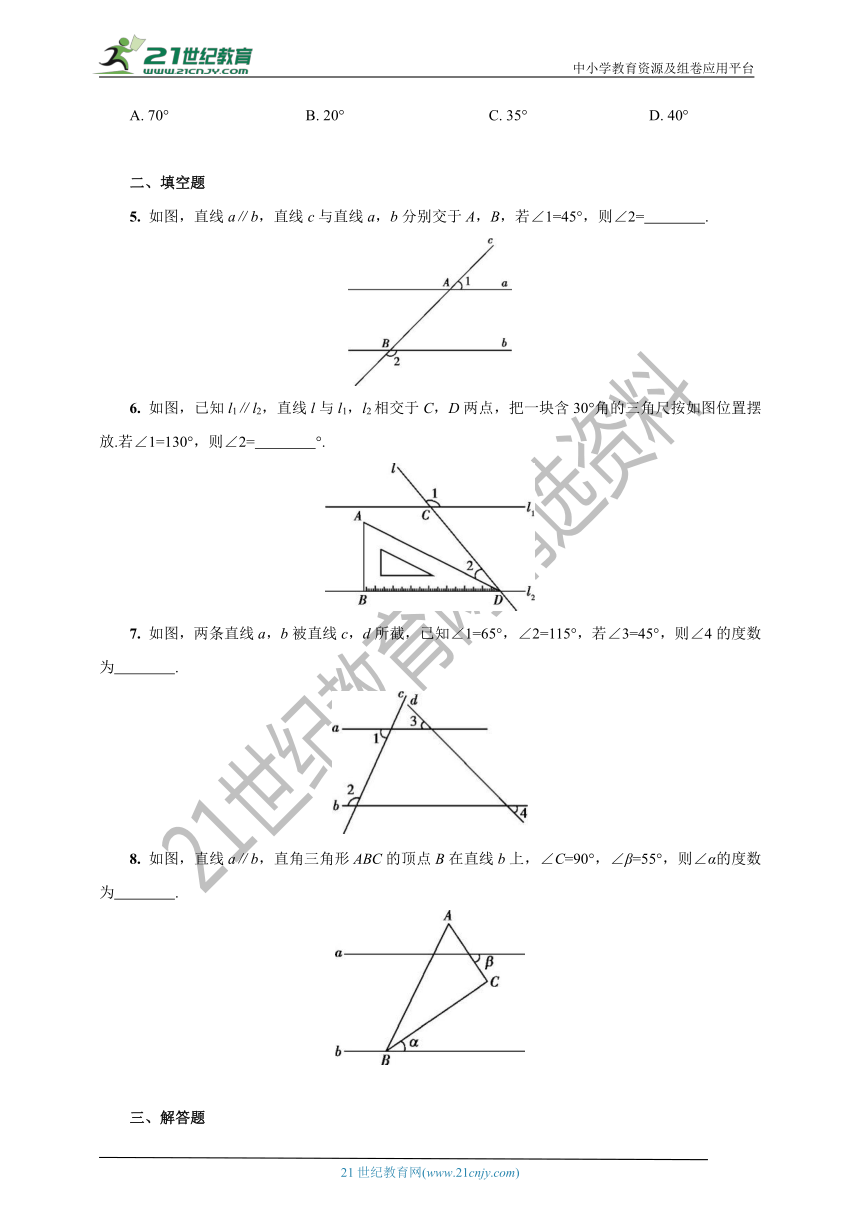
5. 如图，直线a∥b，直线c与直线a，b分别交于A，B，若∠1=45°，则∠2=　　　　.?
6. 如图，已知l1∥l2，直线l与l1，l2相交于C，D两点，把一块含30°角的三角尺按如图位置摆放.若∠1=130°，则∠2=　　　　°.?
7. 如图，两条直线a，b被直线c，d所截，已知∠1=65°，∠2=115°，若∠3=45°，则∠4的度数为　　　　.?
8. 如图，直线a∥b，直角三角形ABC的顶点B在直线b上，∠C=90°，∠β=55°，则∠α的度数为　　　　.?
三、解答题
9. 如图，已知CD⊥AB，GF⊥AB，∠B=∠ADE，试说明∠1=∠2.

10. 如图，已知AB∥CD，EF交AB于点E，交CD于点F，FG平分∠EFD，交AB于点G.若∠1=50°，求∠BGF的度数.

参 考 答 案
1. C　2. D　3. C　4. C　
5. 135°
6. 20
7. 45°
8. 35°
9. 解：∵∠B=∠ADE(已知)，∴DE∥BC(同位角相等，两直线平行)，∴∠1=∠DCB(两直线平行，内错角相等). ∵CD⊥AB，GF⊥AB，∴∠BDC=90°，∠BFG=90°，∴CD∥FG(同位角相等，两直线平行)，∴∠2=∠DCB(两直线平行，同位角相等). ∴∠1=∠2(等量代换).
10. 解：∵AB∥CD，∠1=50°，∴∠CFE=∠1=50°. ∵∠CFE＋∠EFD=180°，∴∠EFD=180°－∠CFE=130°. ∵FG平分∠EFD，∴∠DFG=∠EFD=65°. ∵AB∥CD，∴∠BGF＋∠DFG=180°，∴∠BGF=180°－∠DFG=180°－65°=115°.