人教版 五年级下册找次品(共20张PPT)
文档属性
| 名称 | 人教版 五年级下册找次品(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 521.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-04 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
1986年1月28日,美国挑战者号航天飞机
经过调查发现火箭推进器上面的一个O形环是不合格的零件。
《找次品》
海城第一小学
谢欢碧
有2个O形环,其中有1个是次品(次品比较轻)。你能设法把它找出来吗?
有3个O形环,其中有1个是次品(次品比较轻)。你能利用天平把它找出来吗?
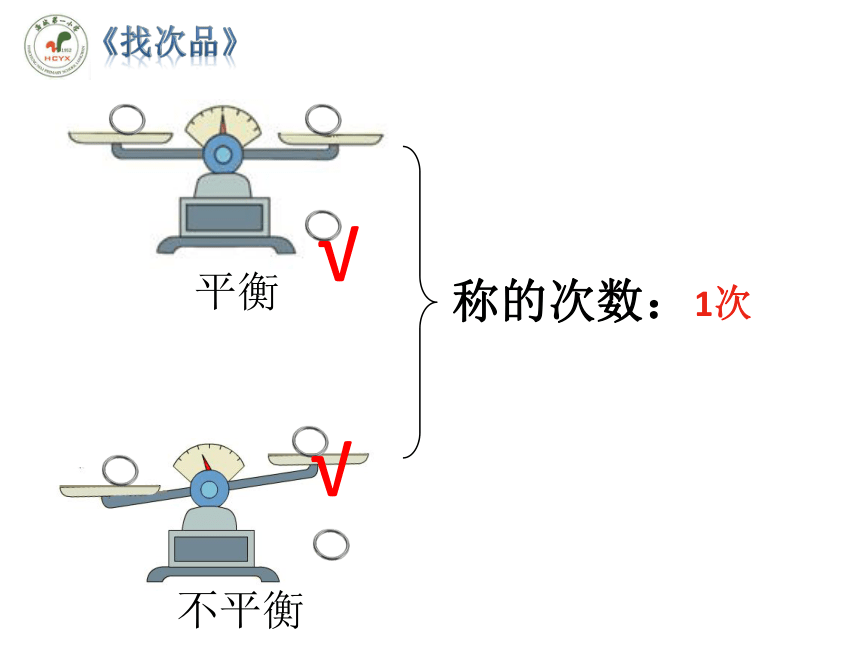
称的次数:
平衡
不平衡
√
√
1次
有8个O形环,其中有1个是次品(次品比较轻)。假如用天平秤,至少秤几次能保证找出次品?
合作要求:
1.小组合作,并用简洁的方式记录你们的推导过程。
2.努力思考更多的办法。
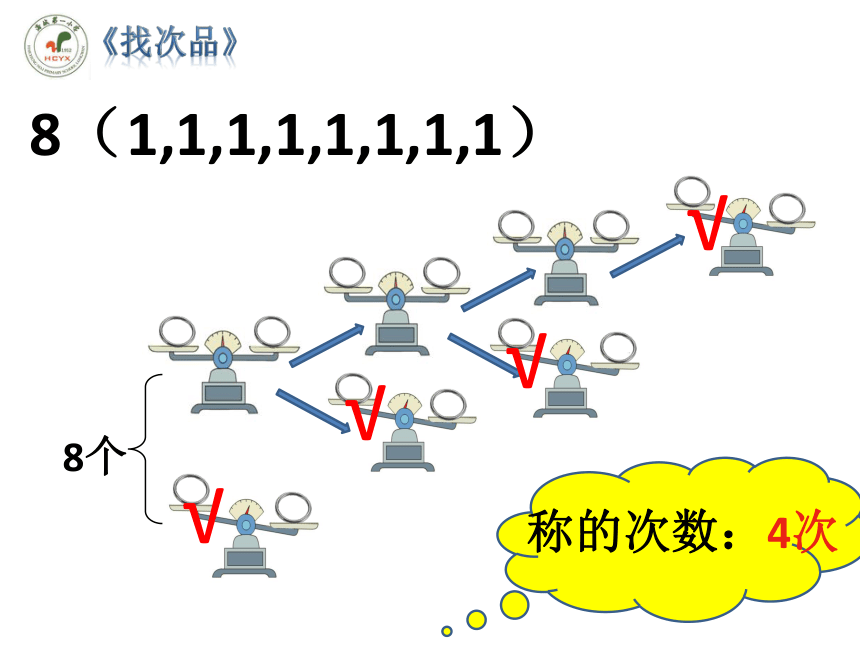
称的次数:4次
8个
8(1,1,1,1,1,1,1,1)
√
√
√
√
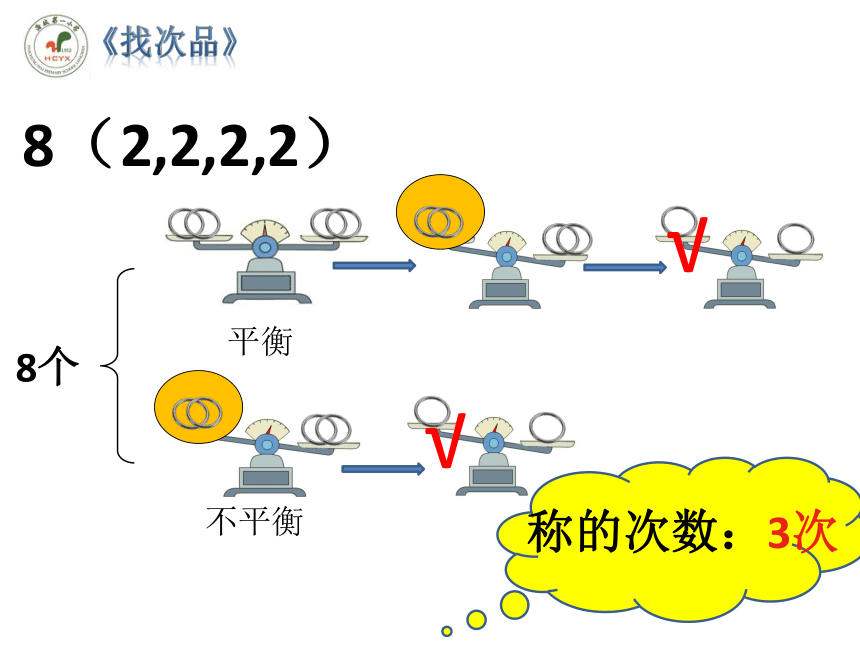
称的次数:3次
不平衡
平衡
8个
8(2,2,2,2)
√
√
称的次数:2次
2个还要1次
不平衡
平衡
8个
3个还要1次
8(3,3,2)
称的次数:3次
不平衡
8个
8(4,4)
√
个数(分组情况) 至少要称的次数
8(1,1,1,1,1,1,1,1) 4次
8(2,2,2,2) 3次
8(3,3,2) 2次
8(4,4) 3次
把8 个被测物品分成3份,能够保证找出次品,而且称的次数最少。
有9个O形环,其中有1个是次品(次品比较轻)。假如用天平秤,至少秤几次能保证找出次品?
合作要求:
1.小组合作,并用简洁的方式记录你们的推导过程。
2.努力思考更多的办法。
称的次数:2次
3个还要1次
不平衡
平衡
9个
3个还要1次
9(3,3,3)
称的次数:3次
不平衡
平衡
9个
√
√
9(4,4,1)
把9 个被测物品平均分成3份,能够保证找出次品,而且称的次数最少。
个数(分组情况) 至少要称的次数
9(3,3,3) 2次
9(4,4,1) 3次
利用天平找次品的时候,把被测物品分成3份,能够平均分的就平均分,不能够平均分的要尽量平均分,多的一份与少的一份相差1。
有27个O形环,其中有1个是次品(次品比较轻)。假如用天平秤,至少秤几次能保证找出次品?
称的次数:3次
9个还要2次
不平衡
平衡
9个还要2次
27个
顺口溜
一个次品混其中,
最优方法来分组。
3的倍数分三份,
不能均分相差一。
放入天平称一称,
次品立即就现形。
这节课你学到了什么?
1986年1月28日,美国挑战者号航天飞机
经过调查发现火箭推进器上面的一个O形环是不合格的零件。
《找次品》
海城第一小学
谢欢碧
有2个O形环,其中有1个是次品(次品比较轻)。你能设法把它找出来吗?
有3个O形环,其中有1个是次品(次品比较轻)。你能利用天平把它找出来吗?
称的次数:
平衡
不平衡
√
√
1次
有8个O形环,其中有1个是次品(次品比较轻)。假如用天平秤,至少秤几次能保证找出次品?
合作要求:
1.小组合作,并用简洁的方式记录你们的推导过程。
2.努力思考更多的办法。
称的次数:4次
8个
8(1,1,1,1,1,1,1,1)
√
√
√
√
称的次数:3次
不平衡
平衡
8个
8(2,2,2,2)
√
√
称的次数:2次
2个还要1次
不平衡
平衡
8个
3个还要1次
8(3,3,2)
称的次数:3次
不平衡
8个
8(4,4)
√
个数(分组情况) 至少要称的次数
8(1,1,1,1,1,1,1,1) 4次
8(2,2,2,2) 3次
8(3,3,2) 2次
8(4,4) 3次
把8 个被测物品分成3份,能够保证找出次品,而且称的次数最少。
有9个O形环,其中有1个是次品(次品比较轻)。假如用天平秤,至少秤几次能保证找出次品?
合作要求:
1.小组合作,并用简洁的方式记录你们的推导过程。
2.努力思考更多的办法。
称的次数:2次
3个还要1次
不平衡
平衡
9个
3个还要1次
9(3,3,3)
称的次数:3次
不平衡
平衡
9个
√
√
9(4,4,1)
把9 个被测物品平均分成3份,能够保证找出次品,而且称的次数最少。
个数(分组情况) 至少要称的次数
9(3,3,3) 2次
9(4,4,1) 3次
利用天平找次品的时候,把被测物品分成3份,能够平均分的就平均分,不能够平均分的要尽量平均分,多的一份与少的一份相差1。
有27个O形环,其中有1个是次品(次品比较轻)。假如用天平秤,至少秤几次能保证找出次品?
称的次数:3次
9个还要2次
不平衡
平衡
9个还要2次
27个
顺口溜
一个次品混其中,
最优方法来分组。
3的倍数分三份,
不能均分相差一。
放入天平称一称,
次品立即就现形。
这节课你学到了什么?
