2020年春北师大八年级数学下册-第07讲-图形的平移与旋转(提高)学案(无答案)
文档属性
| 名称 | 2020年春北师大八年级数学下册-第07讲-图形的平移与旋转(提高)学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 216.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-04 00:00:00 | ||
图片预览




文档简介
学科教师辅导讲义
学员编号:
年 级:八年级(下)
课 时 数:3
学员姓名:
辅导科目:数 学
学科教师:
授课主题
第07讲-图形的平移与旋转
授课类型
T同步课堂
P实战演练
S归纳总结
教学目标
认识图形的平移与旋转;
掌握图形的平移与旋转的性质;
掌握平移与旋转的作图步骤。
授课日期及时段
T(Textbook-Based)——同步课堂
平移
1、平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
平移不改变图形的形状和大小,只改变图形的位置。
2、平移的性质: ①一个图形和它经过平移所得的图形中,对应点所连的线段平行且相等;
②对应线段平行且相等,对应角相等。
3、平移作图的步骤与方法:
一般步骤:(1)分析题目要求,找出平移的方向和平移的距离;
(2)分析所作的图形,找出构成图形的关键点;
(3)沿一定的方向,按一定的距离平移各个关键点;
(4)连接所作的各个关键点,并标上相应的字母;
(5)写出结论。
平移作图的方法:“对应点连接法”和“全等图形法”
4、图形的坐标变化与平移:
(1)纵坐标保持不变,横坐标分别加
①当为正数时,原图形形状、大小不变,向右平移个单位长度;
②当为负数时,原图形形状、大小不变,向左平移个单位长度;
(2)横坐标保持不变,纵坐标分别加
①当为正数时,原图形形状、大小不变,向上平移个单位长度;
②当为负数时,原图形形状、大小不变,向下平移个单位长度;
5、图形平移的变换
(1)图形在坐标系中的平移其实就是点的坐标平移;
(2)一个图形依次沿轴方向、轴方向平移后所得图形,可以看成是由原来的图形经过一次平移得到。
变换的方法:①一次平移的方向是由原图形的点到平移后图形的对应点的方向;②若沿轴方向平移的单位长度为,沿轴方向平移的单位长度为,则原图形经过一次平移的距离为.
旋转
1、旋转的概念
(1)在平面内,将一个图形绕一个定点按某个方向旋转一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角。
(2)旋转不改变图形的大小和形状。
2、旋转的性质
(1)一个图形和它经过旋转所得的图形中,对应点到旋转中心的距离相等,任意一组对应点与旋转中心的连线所成的角都等于旋转角;
(2)对应线段相等,对应角相等。
3、旋转作图的常见形式、步骤与方法
(1)旋转作图常以下列两种形式出现:①已知原图、旋转中心和一对对应点或一对对应线段,做旋转后的图形; ②已知原图、旋转中心、旋转方向和旋转角,作旋转后的图形.
(2)旋转作图的一般步骤:①分析题目要求,找出旋转中心、旋转角;
②分析所作图形,找出构成图形的关键点;
③沿一定的方向,按一定的角度,通过截取线段的方法,旋转各个关键点;
④顺次连接各个关键点的对应点,并标上相应的字母;
⑤写出结论.
考点一:图形的平移
例1、如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
A.16cm B.18cm
C.20cm D.21cm
例2、如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
A.2 B.3
C.4 D.5
例3、如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
A.(﹣2,﹣4) B.(﹣2,4)
C.(2,﹣3) D.(﹣1,﹣3)
例4、在平面直角坐标系中,将点A(m﹣1,n+2)先向右平移3个单位,再向上平移2个单位,得到点
A′,若点A′位于第二象限,则m、n的取值范围分别是( )
A.m<0,n>0 B.m<1,n>﹣2
C.m<0,n<﹣2 D.m<﹣2,m>﹣4
例5、如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm.将线段DC沿着CB的方向平移7cm得到线段EF,点E,F分别落在边AB,BC上,则△EBF的周长为 cm.
例6、如图所示,直线a平移后得到直线b,∠1=60°,∠B=130°,则∠2= °.
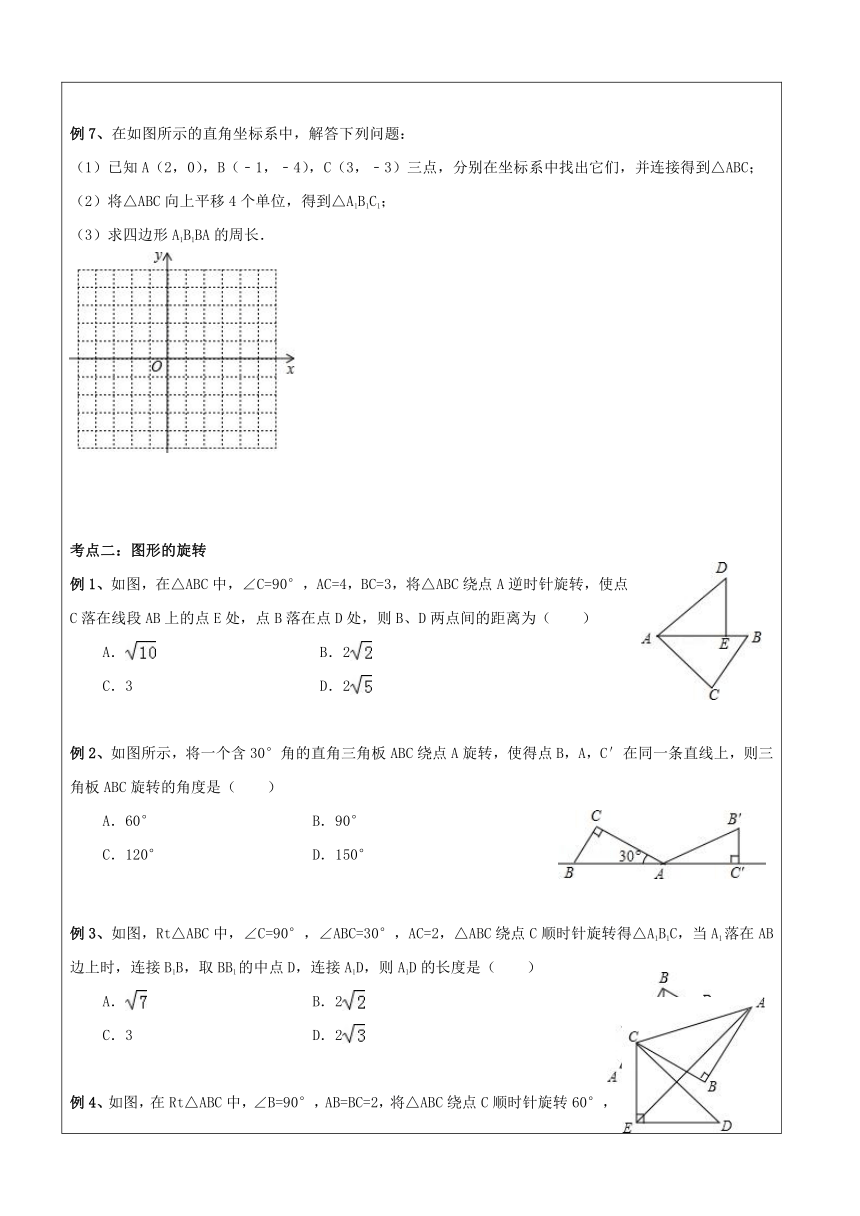
例7、在如图所示的直角坐标系中,解答下列问题:
(1)已知A(2,0),B(﹣1,﹣4),C(3,﹣3)三点,分别在坐标系中找出它们,并连接得到△ABC;
(2)将△ABC向上平移4个单位,得到△A1B1C1;
(3)求四边形A1B1BA的周长.
考点二:图形的旋转
例1、如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )
A. B.2
C.3 D.2
例2、如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是( )
A.60° B.90°
C.120° D.150°
例3、如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
A. B.2
C.3 D.2
例4、如图,在Rt△ABC中,∠B=90°,AB=BC=2,将△ABC绕点C顺时针旋转60°,得到△DEC,则AE的长是 .
例5、如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知
∠A=27°,∠B=40°,则∠ACB′= 度.
例6、在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
P(Practice-Oriented)——实战演练
课堂狙击
1、下列图形中,周长最长的是( )
A. B.
C. D.
2、△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,则下列说法错误的是( )
A.四边形ABED是矩形 B.ADCF
C.BC=CF D.DF=CF
3、如图,两个全等的直角三角形重叠在一起,将Rt△ABC沿着BC的方向平移到Rt△DEF的位置,已知AB=5,DO=2,平移距离为3,则阴影部分的面积为( )
A.12 B.24
C.21 D.20.5
4、在坐标平面上两点A(﹣a+2,﹣b+1)、B(3a,b),若点A向右移动2个单位长度后,再向下移动3个单位长度后与点B重合,则点B所在的坐标为( )
A.(1,﹣1) B.(3,﹣1)
C.(3,﹣3) D.(3,0)
5、如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )
A.4 B.4
C.4 D.8
6、将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“69”旋转180°,得到的数字是( )
A.96 B.69 C.66 D.99
7、如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是( )
A.50° B.60°
C.70° D.80°
8、把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )
A.内部 B.外部
C.边上 D.以上都有可能
9、将点A(1,﹣3)沿x轴向左平移3个单位长度,再沿y轴向上平移5个单位长度后得到的点A′的坐标为 .
10、如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则
BD= .
11、如图,某居民小区有一长方形地,居民想在长方形地内修筑同样宽的两条小路,余下部分绿化,道路的宽为2米,则绿化的面积为多少平方米?
12、如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,将△ABC沿AB方向向右平移得到△DEF,若AE=8cm,DB=2cm.
(1)求△ABC向右平移的距离AD的长;
(2)求四边形AEFC的周长.
课后反击
1、如图,△ABC的面积为2,将△ABC沿AC方向平移至△DFE,且AC=CD,则四边形AEFB的面积为( )
A.6 B.8
C.10 D.12
2、已知△ABC顶点坐标分别是A(0,6),B(﹣3,﹣3),C(1,0),将△ABC平移后顶点A的对应点A1的坐标是(4,10),则点B的对应点B1的坐标为( )
A.(7,1) B.(1,7)
C.(1,1) D.(2,1)
3、如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P( a,b),则点P在A′B′上的对应点P′的坐标为( )
A.(a﹣2,b+3) B.(a﹣2,b﹣3)
C.(a+2,b+3) D.(a+2,b﹣3)
4、如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
A.55° B.65°
C.75° D.85°
5、如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∠A′B′C′可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )
A.4 B.6
C.3 D.3
6、如图所示,将△ABC绕点A按逆时针旋转50°后,得到△ADC′,则∠ABD的度数是( )
A.30° B.45°
C.65° D.75°
7、如图,将△ABC平移到△A′B′C′的位置(点B′在AC边上),若∠B=55°,∠C=100°,则∠AB′A′的度数为 °.
8、在平面直角坐标系中,点P(﹣1,2)向右平移3个单位长度得到的点的坐标是 .
9、如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,则BD= (提示:可连接BE)
10、已知l1∥l2,点A,B在l1上,点C,D在l2上,连接AD,BC.AE,CE分别是∠BAD,∠BCD的角平分线,∠α=70°,∠β=30°.
(1)如图①,求∠AEC的度数;
(2)如图②,将线段AD沿CD方向平移,其他条件不变,求∠AEC的度数.
11、如图,△AOB中,∠AOB=90°,AO=3,BO=6,△AOB绕点O逆时针旋转到△A′OB′处,此时线段A′B′与BO的交点E为BO的中点,求线段B′E的值.
1、若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,则点B的坐标为( )
A.(﹣2,﹣1) B.(﹣1,0)
C.(﹣1,﹣1) D.(﹣2,0)
2、如图,在△ABC中,∠CAB=75°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
A.30° B.40°
C.50° D.75°
S(Summary-Embedded)——归纳总结
1、平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
平移不改变图形的形状和大小,只改变图形的位置。
2、平移的性质: ①一个图形和它经过平移所得的图形中,对应点所连的线段平行且相等;
②对应线段平行且相等,对应角相等。
3、旋转的概念
(1)在平面内,将一个图形绕一个定点按某个方向旋转一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角。
(2)旋转不改变图形的大小和形状。
4、旋转的性质
(1)一个图形和它经过旋转所得的图形中,对应点到旋转中心的距离相等,任意一组对应点与旋转中心的连线所成的角都等于旋转角;
(2)对应线段相等,对应角相等。
图形的平移与旋转,先找到图形平移前后的几个关键点很重要,了解关键点的变化情况,从而得出所有坐标的变化情况,这种由特殊到一般的解决问题的方法,使得复杂的问题变为简单的问题。
本节课我学到
我需要努力的地方是
学员编号:
年 级:八年级(下)
课 时 数:3
学员姓名:
辅导科目:数 学
学科教师:
授课主题
第07讲-图形的平移与旋转
授课类型
T同步课堂
P实战演练
S归纳总结
教学目标
认识图形的平移与旋转;
掌握图形的平移与旋转的性质;
掌握平移与旋转的作图步骤。
授课日期及时段
T(Textbook-Based)——同步课堂
平移
1、平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
平移不改变图形的形状和大小,只改变图形的位置。
2、平移的性质: ①一个图形和它经过平移所得的图形中,对应点所连的线段平行且相等;
②对应线段平行且相等,对应角相等。
3、平移作图的步骤与方法:
一般步骤:(1)分析题目要求,找出平移的方向和平移的距离;
(2)分析所作的图形,找出构成图形的关键点;
(3)沿一定的方向,按一定的距离平移各个关键点;
(4)连接所作的各个关键点,并标上相应的字母;
(5)写出结论。
平移作图的方法:“对应点连接法”和“全等图形法”
4、图形的坐标变化与平移:
(1)纵坐标保持不变,横坐标分别加
①当为正数时,原图形形状、大小不变,向右平移个单位长度;
②当为负数时,原图形形状、大小不变,向左平移个单位长度;
(2)横坐标保持不变,纵坐标分别加
①当为正数时,原图形形状、大小不变,向上平移个单位长度;
②当为负数时,原图形形状、大小不变,向下平移个单位长度;
5、图形平移的变换
(1)图形在坐标系中的平移其实就是点的坐标平移;
(2)一个图形依次沿轴方向、轴方向平移后所得图形,可以看成是由原来的图形经过一次平移得到。
变换的方法:①一次平移的方向是由原图形的点到平移后图形的对应点的方向;②若沿轴方向平移的单位长度为,沿轴方向平移的单位长度为,则原图形经过一次平移的距离为.
旋转
1、旋转的概念
(1)在平面内,将一个图形绕一个定点按某个方向旋转一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角。
(2)旋转不改变图形的大小和形状。
2、旋转的性质
(1)一个图形和它经过旋转所得的图形中,对应点到旋转中心的距离相等,任意一组对应点与旋转中心的连线所成的角都等于旋转角;
(2)对应线段相等,对应角相等。
3、旋转作图的常见形式、步骤与方法
(1)旋转作图常以下列两种形式出现:①已知原图、旋转中心和一对对应点或一对对应线段,做旋转后的图形; ②已知原图、旋转中心、旋转方向和旋转角,作旋转后的图形.
(2)旋转作图的一般步骤:①分析题目要求,找出旋转中心、旋转角;
②分析所作图形,找出构成图形的关键点;
③沿一定的方向,按一定的角度,通过截取线段的方法,旋转各个关键点;
④顺次连接各个关键点的对应点,并标上相应的字母;
⑤写出结论.
考点一:图形的平移
例1、如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
A.16cm B.18cm
C.20cm D.21cm
例2、如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
A.2 B.3
C.4 D.5
例3、如图,将△PQR向右平移2个单位长度,再向下平移3个单位长度,则顶点P平移后的坐标是( )
A.(﹣2,﹣4) B.(﹣2,4)
C.(2,﹣3) D.(﹣1,﹣3)
例4、在平面直角坐标系中,将点A(m﹣1,n+2)先向右平移3个单位,再向上平移2个单位,得到点
A′,若点A′位于第二象限,则m、n的取值范围分别是( )
A.m<0,n>0 B.m<1,n>﹣2
C.m<0,n<﹣2 D.m<﹣2,m>﹣4
例5、如图,△ABC中,AB=AC,BC=12cm,点D在AC上,DC=4cm.将线段DC沿着CB的方向平移7cm得到线段EF,点E,F分别落在边AB,BC上,则△EBF的周长为 cm.
例6、如图所示,直线a平移后得到直线b,∠1=60°,∠B=130°,则∠2= °.
例7、在如图所示的直角坐标系中,解答下列问题:
(1)已知A(2,0),B(﹣1,﹣4),C(3,﹣3)三点,分别在坐标系中找出它们,并连接得到△ABC;
(2)将△ABC向上平移4个单位,得到△A1B1C1;
(3)求四边形A1B1BA的周长.
考点二:图形的旋转
例1、如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )
A. B.2
C.3 D.2
例2、如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是( )
A.60° B.90°
C.120° D.150°
例3、如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
A. B.2
C.3 D.2
例4、如图,在Rt△ABC中,∠B=90°,AB=BC=2,将△ABC绕点C顺时针旋转60°,得到△DEC,则AE的长是 .
例5、如图,将△ABC绕点C按顺时针方向旋转至△A′B′C,使点A′落在BC的延长线上.已知
∠A=27°,∠B=40°,则∠ACB′= 度.
例6、在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
P(Practice-Oriented)——实战演练
课堂狙击
1、下列图形中,周长最长的是( )
A. B.
C. D.
2、△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,则下列说法错误的是( )
A.四边形ABED是矩形 B.ADCF
C.BC=CF D.DF=CF
3、如图,两个全等的直角三角形重叠在一起,将Rt△ABC沿着BC的方向平移到Rt△DEF的位置,已知AB=5,DO=2,平移距离为3,则阴影部分的面积为( )
A.12 B.24
C.21 D.20.5
4、在坐标平面上两点A(﹣a+2,﹣b+1)、B(3a,b),若点A向右移动2个单位长度后,再向下移动3个单位长度后与点B重合,则点B所在的坐标为( )
A.(1,﹣1) B.(3,﹣1)
C.(3,﹣3) D.(3,0)
5、如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )
A.4 B.4
C.4 D.8
6、将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”,现将数字“69”旋转180°,得到的数字是( )
A.96 B.69 C.66 D.99
7、如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是( )
A.50° B.60°
C.70° D.80°
8、把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )
A.内部 B.外部
C.边上 D.以上都有可能
9、将点A(1,﹣3)沿x轴向左平移3个单位长度,再沿y轴向上平移5个单位长度后得到的点A′的坐标为 .
10、如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则
BD= .
11、如图,某居民小区有一长方形地,居民想在长方形地内修筑同样宽的两条小路,余下部分绿化,道路的宽为2米,则绿化的面积为多少平方米?
12、如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,将△ABC沿AB方向向右平移得到△DEF,若AE=8cm,DB=2cm.
(1)求△ABC向右平移的距离AD的长;
(2)求四边形AEFC的周长.
课后反击
1、如图,△ABC的面积为2,将△ABC沿AC方向平移至△DFE,且AC=CD,则四边形AEFB的面积为( )
A.6 B.8
C.10 D.12
2、已知△ABC顶点坐标分别是A(0,6),B(﹣3,﹣3),C(1,0),将△ABC平移后顶点A的对应点A1的坐标是(4,10),则点B的对应点B1的坐标为( )
A.(7,1) B.(1,7)
C.(1,1) D.(2,1)
3、如图,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P( a,b),则点P在A′B′上的对应点P′的坐标为( )
A.(a﹣2,b+3) B.(a﹣2,b﹣3)
C.(a+2,b+3) D.(a+2,b﹣3)
4、如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
A.55° B.65°
C.75° D.85°
5、如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∠A′B′C′可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( )
A.4 B.6
C.3 D.3
6、如图所示,将△ABC绕点A按逆时针旋转50°后,得到△ADC′,则∠ABD的度数是( )
A.30° B.45°
C.65° D.75°
7、如图,将△ABC平移到△A′B′C′的位置(点B′在AC边上),若∠B=55°,∠C=100°,则∠AB′A′的度数为 °.
8、在平面直角坐标系中,点P(﹣1,2)向右平移3个单位长度得到的点的坐标是 .
9、如图,在四边形ABCD中,∠ABC=30°,将△DCB绕点C顺时针旋转60°后,点D的对应点恰好与点A重合,得到△ACE,若AB=3,BC=4,则BD= (提示:可连接BE)
10、已知l1∥l2,点A,B在l1上,点C,D在l2上,连接AD,BC.AE,CE分别是∠BAD,∠BCD的角平分线,∠α=70°,∠β=30°.
(1)如图①,求∠AEC的度数;
(2)如图②,将线段AD沿CD方向平移,其他条件不变,求∠AEC的度数.
11、如图,△AOB中,∠AOB=90°,AO=3,BO=6,△AOB绕点O逆时针旋转到△A′OB′处,此时线段A′B′与BO的交点E为BO的中点,求线段B′E的值.
1、若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,则点B的坐标为( )
A.(﹣2,﹣1) B.(﹣1,0)
C.(﹣1,﹣1) D.(﹣2,0)
2、如图,在△ABC中,∠CAB=75°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
A.30° B.40°
C.50° D.75°
S(Summary-Embedded)——归纳总结
1、平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
平移不改变图形的形状和大小,只改变图形的位置。
2、平移的性质: ①一个图形和它经过平移所得的图形中,对应点所连的线段平行且相等;
②对应线段平行且相等,对应角相等。
3、旋转的概念
(1)在平面内,将一个图形绕一个定点按某个方向旋转一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角。
(2)旋转不改变图形的大小和形状。
4、旋转的性质
(1)一个图形和它经过旋转所得的图形中,对应点到旋转中心的距离相等,任意一组对应点与旋转中心的连线所成的角都等于旋转角;
(2)对应线段相等,对应角相等。
图形的平移与旋转,先找到图形平移前后的几个关键点很重要,了解关键点的变化情况,从而得出所有坐标的变化情况,这种由特殊到一般的解决问题的方法,使得复杂的问题变为简单的问题。
本节课我学到
我需要努力的地方是
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
