中考培优第二轮复习专题 第1章 慧眼识平行学案(含答案)
文档属性
| 名称 | 中考培优第二轮复习专题 第1章 慧眼识平行学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 12:01:40 | ||
图片预览



文档简介
第一章 慧眼识平行
平行和垂直是几何问题中非常重要的两种位置关系,由于这两种关系极其具有本质性,所以许多题的突破点就在这里,一旦发现了这些结论,对于解题会有相当大的帮助!
两直线平行,除了直接的:①同位角相等;②内错角相等;③同旁内角互补,还有一些其它基本图中也暗藏着平行,这需要同学们通过模式识别,找出题中的平行来,以此解决接下来的问题.
一、同侧共边三角形面积相等
例题1、如图,将□ABCD沿着对角线AC翻折,点B落在点E
处,连接ED,求证:ED//AC.
【解答】如图,连接ED.在□ABCD中,,由翻折知,,∴ED//AC.
例题2、在□ABCD中,AB<BC,已知∠B=30°,AB=,将△ABC沿AC翻折至△ABC,使点B'落在□ABCD所在的平面内,连接B'D.若△AB'D是直角三角形,则BC的长为________.
【解答】4或6.
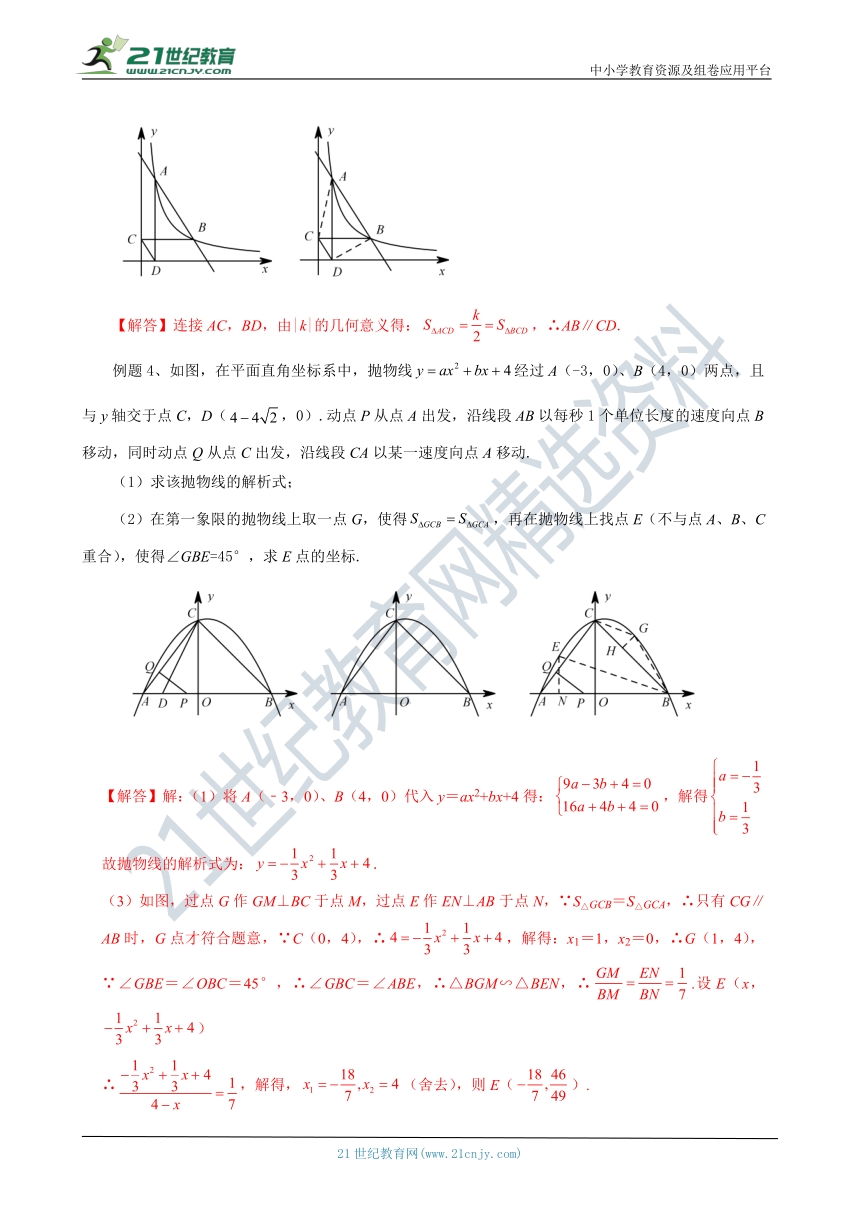
例题3、如图,一次函数y=k1x+b与反比例函数交于A、B两点,过点A、B分别作x轴、y轴垂线,垂足分别为D、C,连接CD,求证:CD//AB.
【解答】连接AC,BD,由|k|的几何意义得:,∴AB∥CD.
例题4、如图,在平面直角坐标系中,抛物线经过A(-3,0)、B(4,0)两点,且与y轴交于点C,D(,0).动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.
(1)求该抛物线的解析式;
(2)在第一象限的抛物线上取一点G,使得,再在抛物线上找点E(不与点A、B、C重合),使得∠GBE=45°,求E点的坐标.
【解答】解:(1)将A(﹣3,0)、B(4,0)代入y=ax2+bx+4得:,解得
故抛物线的解析式为:.
(3)如图,过点G作GM⊥BC于点M,过点E作EN⊥AB于点N,∵S△GCB=S△GCA,∴只有CG∥AB时,G点才符合题意,∵C(0,4),∴,解得:x1=1,x2=0,∴G(1,4),∵∠GBE=∠OBC=45°,∴∠GBC=∠ABE,∴△BGM∽△BEN,∴.设E(x,)
∴,解得,(舍去),则E().
即时练习
1、已知抛物线(a<0)与x轴交于点A(8,0)和B(-12,0),与y轴交于点C(0,6).
(1)求该抛物线的解析式;
(2)在第二象限的抛物线上取一点P,使得,再在抛物线上找一点Q(不与点A、B、C重合),使得tan∠PBQ=,求点Q的坐标.
【解答】解:(1)∵抛物线y=ax2+bx+c(a<0)与x轴交于点A(8,0)和B(﹣12,0),∴可设抛物线的解析式为y=a(x﹣8)(x+12),又∵抛物线过点C(0,6),∴6=﹣96a,解得a=,
∴,即该抛物线的解析式为;
(2)∵S△PCA=S△PCB,∴A、B到PC的距离相等,∴PC∥AB,∴P、C关于抛物线的对称轴x=﹣2对称,∵C(0,6),∴P(﹣4,6).∵tan∠PBQ=,,∴∠PBQ=∠CBA,∴∠PBQ﹣∠CBQ=∠CBA﹣∠CBQ,即∠PBC=∠QBA.作PG⊥BC于G,QH⊥AB于H.∵,,BG=BC﹣CG==,∴设点Q的坐标为(x,),∵tan∠QBA=tan∠PBC,∴,解得或-12(舍去),故点Q的坐标是(,).
二、角平分线+等腰
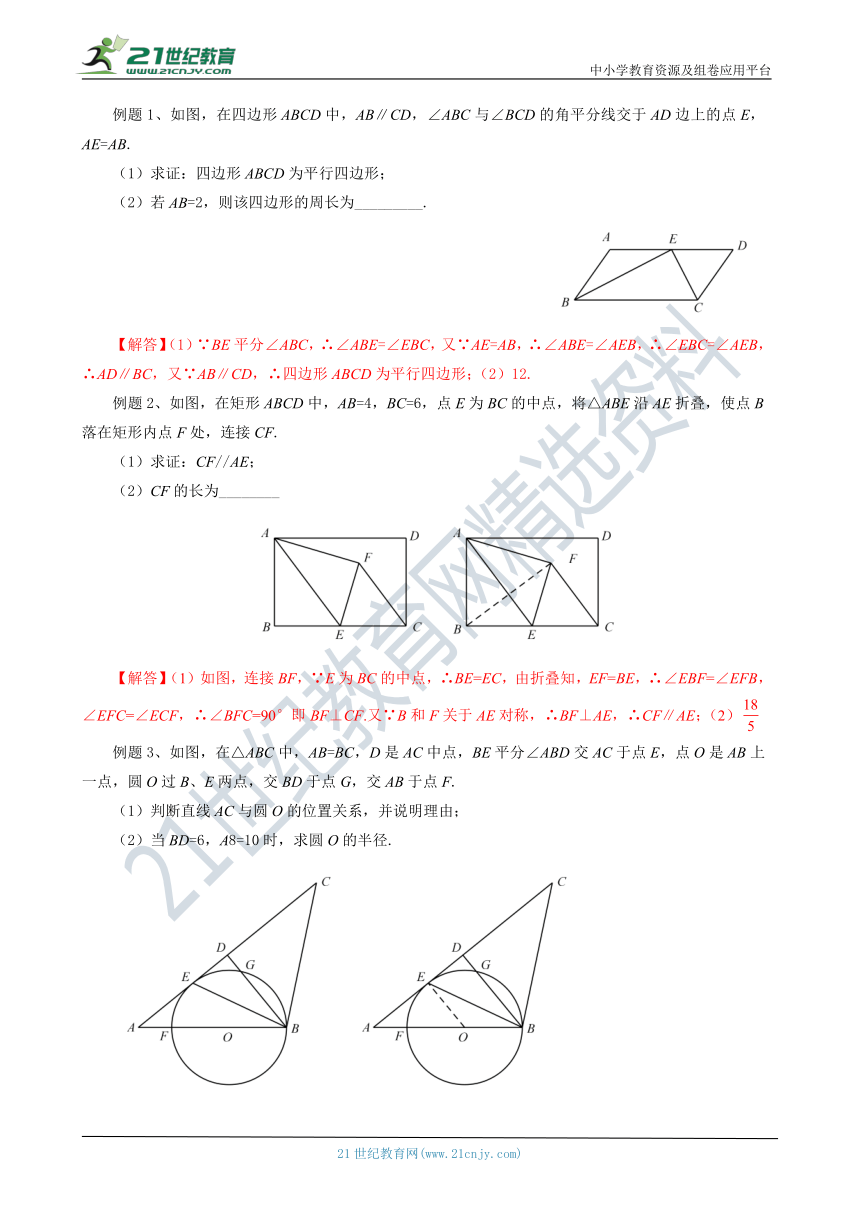
例题1、如图,在四边形ABCD中,AB∥CD,∠ABC与∠BCD的角平分线交于AD边上的点E,AE=AB.
(1)求证:四边形ABCD为平行四边形;
(2)若AB=2,则该四边形的周长为_________.
【解答】(1)∵BE平分∠ABC,∴∠ABE=∠EBC,又∵AE=AB,∴∠ABE=∠AEB,∴∠EBC=∠AEB,∴AD∥BC,又∵AB∥CD,∴四边形ABCD为平行四边形;(2)12.
例题2、如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF.
(1)求证:CF//AE;
(2)CF的长为________
【解答】(1)如图,连接BF,∵E为BC的中点,∴BE=EC,由折叠知,EF=BE,∴∠EBF=∠EFB,∠EFC=∠ECF,∴∠BFC=90°即BF⊥CF.又∵B和F关于AE对称,∴BF⊥AE,∴CF∥AE;(2)
例题3、如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,圆O过B、E两点,交BD于点G,交AB于点F.
(1)判断直线AC与圆O的位置关系,并说明理由;
(2)当BD=6,A8=10时,求圆O的半径.
【解答】解:(1)AC与⊙O相切.理由如下:连结OE,如图,∵BE平分∠ABD,∴∠OBE=∠DBO,∵OE=OB,∴∠OBE=∠OEB,∴∠OBE=∠DBO,∴OE∥BD,∵AB=BC,D是AC中点,∴BD⊥AC,∴OE⊥AC,∴AC与⊙O相切;
(2)设⊙O半径为r,则AO=10﹣r,由(1)知,OE∥BD,∴△AOE∽△ABD,∴,即
,∴,即⊙O半径是.
即时练习
1、如图,□ABCD中,点E为AB边上的中点,点F在BC边上,连接EF,将△BEF沿着EF翻折,点B落在B’处,连接AB’,写出该图中与∠BEF所有相等的角:________;
【解答】∠B’EF,∠EAB’,∠EB’A.
2、如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于________.
【解答】解:如图连接BE交AD于O,作AH⊥BC于H.在Rt△ABC中,∵AC=4,AB=3,∴BC==5,∵CD=DB,∴AD=DC=DB=,∵?BC?AH=?AB?AC,∴AH=,∵AE=AB,∴点A在BE的垂直平分线上.∵DE=DB=DC,∴点D在BE的垂直平分线上,△BCE是直角三角形,∴AD垂直平分线段BE,∵?AD?BO=?BD?AH,∴OB=,∴BE=2OB=,在Rt△BCE中,EC===,故答案为:.
3、已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的圆O交BC于点G,交AB于点F,FB恰为圆O的直径.
(1)求证:AE与圆O相切;
(2)当BC=4,cosC=时,求圆O的半径.
【解答】(1)证明:连接OM,则OM=OB∴∠1=∠2,∵BM平分∠ABC,∴∠1=∠3,∴∠2=∠3,∴OM∥BC,∴∠AMO=∠AEB,在△ABC中,AB=AC,AE是角平分线,∴AE⊥BC,∴∠AEB=90°∴∠AMO=90°,∴OM⊥AE,∵点M在圆O上,∴AE与⊙O相切;
(2)解:在△ABC中,AB=AC,AE是角平分线∴BE=BC,∠ABC=∠C,∵BC=4,cosC=
∴BE=2,cos∠ABC=,在△ABE中,∠AEB=90°,∴AB==6,设⊙O的半径为r,则AO=6﹣r,∵OM∥BC,∴△AOM∽△ABE,∴,∴,解得:.∴⊙O的半径为.
三、“k”相等
例题1、已知四边形ABCD的各点坐标分别为A(0,0)、B(5,0)、C(m+2,3)、D(m-3,3),若一次函数恰好平分该四边形面积,则m的值为________.
【解答】.
例题2、若与之间的距离为4,则b=________.
【解答】4或-6.
四、中位线(暗藏中点》
例题1、如图,过点B作等腰Rt△ABC的角平分线的垂线,垂足为D,点E为AB中点,连接DE,已知AB=2.
(1)DE的长为________;
(2)点F为CD与AB的交点,则EF=________.
【解答】(1);(2).
例题2、如图,以△ABC中的AB边为直径作圆O交AC中点D,连接BD、OC交于点E,已知AB=2,∠A=30°,则OE的长为________.
【解答】.
五、利用特殊四边形证平行
例题1、如图,已知△ABC为等腰直角三角形,AB=BC,∠ABC=90°,点D是CB延长线上一点,连接DA,以DA为直角边向左侧作等腰直角三角形,AD=DE,∠ADE=90°(如图所示),在AB上取一点F,使得BF=BD,连接EF.求证:EF∥BC.
【解答】如图,延长线段CF与AD相交于点H.∵AB=BC,∠ABC=∠DBA,BD=BF,∴△ABD≌△CBF.∴∠FCB=∠BAD,∴∠BAD+∠AFH=90°,∴∠AHF=90°即CF⊥AD.又∵ED⊥AD,∴CF∥ED.
例题2、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC,交CD于K,交BC于E,F是BE上一点,且BF=CE.求证:FK∥AB.
证明:过点K作MK∥BC,∵AE平分∠BAC,∴∠BAE=∠CAE,又∵∠ACB=90°,CD⊥AB,∴∠BAE+∠DKA=∠CAE+∠CEA=90°,∴∠DKA=∠CEA,又∵∠DKA=∠CKE,∴∠CEA=∠CKE,∴CE=CK,又∵CE=BF,∴CK=BF,而MK∥BC,∴∠B=∠AMK,∴∠BCD+∠B=∠DCA+∠BCD=90°,∴∠AMK=∠DCA.∴在△AMK和△ACK中,∠AMK=∠ACK,AK=AK,∠MAK=∠CAK,.△AMK≌△ACK,∴CK=MK,∴MK=BF,MK∥BF,∴四边形BFKM是平行四边形,∴FK//AB.
六、成比例线段平行
例题1、如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.当P异于A、C时,请说明PQ//BC;
【解答】连接BD交AC于点O.∵四边形ABCD是菱形,且边长为2cm,∠DAB=60°,∴AB=BC=2,∠BAC=∠BAD=30°,∵AC⊥BD,OA=AC=,∴AC=2,∵AB=2,AP=t,AQ=t,∴.即,又∵∠PAQ=∠CAB,∴△PAQ∽△CAB,∴∠APQ=∠ACB,∴PQ∥BC.
例题2、已知二次函数,其图象抛物线交x轴于点A(1,0),B(3,0),交y轴于点C,直线l过点C,且交抛物线于另一点E(点E不与点A、B重合).
(1)求此二次函数关系式;
(2)若过点A作AG⊥x轴,交直线l于点G,连接OG、BE,试证明:OG//BE.
【解答】解:(1)二次函数y=x2+bx+c,其图象抛物线交x轴于点A(1,0),B(3,0),∴,
解得:,∴此二次函数关系式为:y=x2﹣4x+3;
(2)如图②,过点E作EH⊥x轴于点H,设直线CE的解析式为:y=kx+3,∵A(1,0),AG⊥x轴,∴点G(1,k+3),即OA=1,AG=k+3,∵E是直线与抛物线的交点,∴,解得:,∴点E(k+4,(k+1)(k+3)),∴BH=OH﹣OB=k+1,EH=(k+1)(k+3),∴,∵∠OAG=∠BHE=90°,∴△OAG∽△BHE,∴∠AOG=∠HBE,∴OG∥BE.
即时练习
1、如图,△AOB中,∠O=90°,AO=8cm,BO=6cm,点C从A点出发,在边AO上以2cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以1.5cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,
(1)求证:直线EF⊥AB;
(2)当点C运动了_________s时,以C点为圆心,1.5cm为半径的圆与直线CF相切.
【解答】(1)设运动的时间为t,∴AC=2t,BD=1.5t,∴AC:AO=t:4,BD:BO=t:4,∴AC:AO=BD:BO,即CD∥AB,∵EF⊥CD,∴EF⊥AB.(2)
平行和垂直是几何问题中非常重要的两种位置关系,由于这两种关系极其具有本质性,所以许多题的突破点就在这里,一旦发现了这些结论,对于解题会有相当大的帮助!
两直线平行,除了直接的:①同位角相等;②内错角相等;③同旁内角互补,还有一些其它基本图中也暗藏着平行,这需要同学们通过模式识别,找出题中的平行来,以此解决接下来的问题.
一、同侧共边三角形面积相等
例题1、如图,将□ABCD沿着对角线AC翻折,点B落在点E
处,连接ED,求证:ED//AC.
【解答】如图,连接ED.在□ABCD中,,由翻折知,,∴ED//AC.
例题2、在□ABCD中,AB<BC,已知∠B=30°,AB=,将△ABC沿AC翻折至△ABC,使点B'落在□ABCD所在的平面内,连接B'D.若△AB'D是直角三角形,则BC的长为________.
【解答】4或6.
例题3、如图,一次函数y=k1x+b与反比例函数交于A、B两点,过点A、B分别作x轴、y轴垂线,垂足分别为D、C,连接CD,求证:CD//AB.
【解答】连接AC,BD,由|k|的几何意义得:,∴AB∥CD.
例题4、如图,在平面直角坐标系中,抛物线经过A(-3,0)、B(4,0)两点,且与y轴交于点C,D(,0).动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.
(1)求该抛物线的解析式;
(2)在第一象限的抛物线上取一点G,使得,再在抛物线上找点E(不与点A、B、C重合),使得∠GBE=45°,求E点的坐标.
【解答】解:(1)将A(﹣3,0)、B(4,0)代入y=ax2+bx+4得:,解得
故抛物线的解析式为:.
(3)如图,过点G作GM⊥BC于点M,过点E作EN⊥AB于点N,∵S△GCB=S△GCA,∴只有CG∥AB时,G点才符合题意,∵C(0,4),∴,解得:x1=1,x2=0,∴G(1,4),∵∠GBE=∠OBC=45°,∴∠GBC=∠ABE,∴△BGM∽△BEN,∴.设E(x,)
∴,解得,(舍去),则E().
即时练习
1、已知抛物线(a<0)与x轴交于点A(8,0)和B(-12,0),与y轴交于点C(0,6).
(1)求该抛物线的解析式;
(2)在第二象限的抛物线上取一点P,使得,再在抛物线上找一点Q(不与点A、B、C重合),使得tan∠PBQ=,求点Q的坐标.
【解答】解:(1)∵抛物线y=ax2+bx+c(a<0)与x轴交于点A(8,0)和B(﹣12,0),∴可设抛物线的解析式为y=a(x﹣8)(x+12),又∵抛物线过点C(0,6),∴6=﹣96a,解得a=,
∴,即该抛物线的解析式为;
(2)∵S△PCA=S△PCB,∴A、B到PC的距离相等,∴PC∥AB,∴P、C关于抛物线的对称轴x=﹣2对称,∵C(0,6),∴P(﹣4,6).∵tan∠PBQ=,,∴∠PBQ=∠CBA,∴∠PBQ﹣∠CBQ=∠CBA﹣∠CBQ,即∠PBC=∠QBA.作PG⊥BC于G,QH⊥AB于H.∵,,BG=BC﹣CG==,∴设点Q的坐标为(x,),∵tan∠QBA=tan∠PBC,∴,解得或-12(舍去),故点Q的坐标是(,).
二、角平分线+等腰
例题1、如图,在四边形ABCD中,AB∥CD,∠ABC与∠BCD的角平分线交于AD边上的点E,AE=AB.
(1)求证:四边形ABCD为平行四边形;
(2)若AB=2,则该四边形的周长为_________.
【解答】(1)∵BE平分∠ABC,∴∠ABE=∠EBC,又∵AE=AB,∴∠ABE=∠AEB,∴∠EBC=∠AEB,∴AD∥BC,又∵AB∥CD,∴四边形ABCD为平行四边形;(2)12.
例题2、如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF.
(1)求证:CF//AE;
(2)CF的长为________
【解答】(1)如图,连接BF,∵E为BC的中点,∴BE=EC,由折叠知,EF=BE,∴∠EBF=∠EFB,∠EFC=∠ECF,∴∠BFC=90°即BF⊥CF.又∵B和F关于AE对称,∴BF⊥AE,∴CF∥AE;(2)
例题3、如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,圆O过B、E两点,交BD于点G,交AB于点F.
(1)判断直线AC与圆O的位置关系,并说明理由;
(2)当BD=6,A8=10时,求圆O的半径.
【解答】解:(1)AC与⊙O相切.理由如下:连结OE,如图,∵BE平分∠ABD,∴∠OBE=∠DBO,∵OE=OB,∴∠OBE=∠OEB,∴∠OBE=∠DBO,∴OE∥BD,∵AB=BC,D是AC中点,∴BD⊥AC,∴OE⊥AC,∴AC与⊙O相切;
(2)设⊙O半径为r,则AO=10﹣r,由(1)知,OE∥BD,∴△AOE∽△ABD,∴,即
,∴,即⊙O半径是.
即时练习
1、如图,□ABCD中,点E为AB边上的中点,点F在BC边上,连接EF,将△BEF沿着EF翻折,点B落在B’处,连接AB’,写出该图中与∠BEF所有相等的角:________;
【解答】∠B’EF,∠EAB’,∠EB’A.
2、如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于________.
【解答】解:如图连接BE交AD于O,作AH⊥BC于H.在Rt△ABC中,∵AC=4,AB=3,∴BC==5,∵CD=DB,∴AD=DC=DB=,∵?BC?AH=?AB?AC,∴AH=,∵AE=AB,∴点A在BE的垂直平分线上.∵DE=DB=DC,∴点D在BE的垂直平分线上,△BCE是直角三角形,∴AD垂直平分线段BE,∵?AD?BO=?BD?AH,∴OB=,∴BE=2OB=,在Rt△BCE中,EC===,故答案为:.
3、已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的圆O交BC于点G,交AB于点F,FB恰为圆O的直径.
(1)求证:AE与圆O相切;
(2)当BC=4,cosC=时,求圆O的半径.
【解答】(1)证明:连接OM,则OM=OB∴∠1=∠2,∵BM平分∠ABC,∴∠1=∠3,∴∠2=∠3,∴OM∥BC,∴∠AMO=∠AEB,在△ABC中,AB=AC,AE是角平分线,∴AE⊥BC,∴∠AEB=90°∴∠AMO=90°,∴OM⊥AE,∵点M在圆O上,∴AE与⊙O相切;
(2)解:在△ABC中,AB=AC,AE是角平分线∴BE=BC,∠ABC=∠C,∵BC=4,cosC=
∴BE=2,cos∠ABC=,在△ABE中,∠AEB=90°,∴AB==6,设⊙O的半径为r,则AO=6﹣r,∵OM∥BC,∴△AOM∽△ABE,∴,∴,解得:.∴⊙O的半径为.
三、“k”相等
例题1、已知四边形ABCD的各点坐标分别为A(0,0)、B(5,0)、C(m+2,3)、D(m-3,3),若一次函数恰好平分该四边形面积,则m的值为________.
【解答】.
例题2、若与之间的距离为4,则b=________.
【解答】4或-6.
四、中位线(暗藏中点》
例题1、如图,过点B作等腰Rt△ABC的角平分线的垂线,垂足为D,点E为AB中点,连接DE,已知AB=2.
(1)DE的长为________;
(2)点F为CD与AB的交点,则EF=________.
【解答】(1);(2).
例题2、如图,以△ABC中的AB边为直径作圆O交AC中点D,连接BD、OC交于点E,已知AB=2,∠A=30°,则OE的长为________.
【解答】.
五、利用特殊四边形证平行
例题1、如图,已知△ABC为等腰直角三角形,AB=BC,∠ABC=90°,点D是CB延长线上一点,连接DA,以DA为直角边向左侧作等腰直角三角形,AD=DE,∠ADE=90°(如图所示),在AB上取一点F,使得BF=BD,连接EF.求证:EF∥BC.
【解答】如图,延长线段CF与AD相交于点H.∵AB=BC,∠ABC=∠DBA,BD=BF,∴△ABD≌△CBF.∴∠FCB=∠BAD,∴∠BAD+∠AFH=90°,∴∠AHF=90°即CF⊥AD.又∵ED⊥AD,∴CF∥ED.
例题2、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC,交CD于K,交BC于E,F是BE上一点,且BF=CE.求证:FK∥AB.
证明:过点K作MK∥BC,∵AE平分∠BAC,∴∠BAE=∠CAE,又∵∠ACB=90°,CD⊥AB,∴∠BAE+∠DKA=∠CAE+∠CEA=90°,∴∠DKA=∠CEA,又∵∠DKA=∠CKE,∴∠CEA=∠CKE,∴CE=CK,又∵CE=BF,∴CK=BF,而MK∥BC,∴∠B=∠AMK,∴∠BCD+∠B=∠DCA+∠BCD=90°,∴∠AMK=∠DCA.∴在△AMK和△ACK中,∠AMK=∠ACK,AK=AK,∠MAK=∠CAK,.△AMK≌△ACK,∴CK=MK,∴MK=BF,MK∥BF,∴四边形BFKM是平行四边形,∴FK//AB.
六、成比例线段平行
例题1、如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts.当P异于A、C时,请说明PQ//BC;
【解答】连接BD交AC于点O.∵四边形ABCD是菱形,且边长为2cm,∠DAB=60°,∴AB=BC=2,∠BAC=∠BAD=30°,∵AC⊥BD,OA=AC=,∴AC=2,∵AB=2,AP=t,AQ=t,∴.即,又∵∠PAQ=∠CAB,∴△PAQ∽△CAB,∴∠APQ=∠ACB,∴PQ∥BC.
例题2、已知二次函数,其图象抛物线交x轴于点A(1,0),B(3,0),交y轴于点C,直线l过点C,且交抛物线于另一点E(点E不与点A、B重合).
(1)求此二次函数关系式;
(2)若过点A作AG⊥x轴,交直线l于点G,连接OG、BE,试证明:OG//BE.
【解答】解:(1)二次函数y=x2+bx+c,其图象抛物线交x轴于点A(1,0),B(3,0),∴,
解得:,∴此二次函数关系式为:y=x2﹣4x+3;
(2)如图②,过点E作EH⊥x轴于点H,设直线CE的解析式为:y=kx+3,∵A(1,0),AG⊥x轴,∴点G(1,k+3),即OA=1,AG=k+3,∵E是直线与抛物线的交点,∴,解得:,∴点E(k+4,(k+1)(k+3)),∴BH=OH﹣OB=k+1,EH=(k+1)(k+3),∴,∵∠OAG=∠BHE=90°,∴△OAG∽△BHE,∴∠AOG=∠HBE,∴OG∥BE.
即时练习
1、如图,△AOB中,∠O=90°,AO=8cm,BO=6cm,点C从A点出发,在边AO上以2cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以1.5cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,
(1)求证:直线EF⊥AB;
(2)当点C运动了_________s时,以C点为圆心,1.5cm为半径的圆与直线CF相切.
【解答】(1)设运动的时间为t,∴AC=2t,BD=1.5t,∴AC:AO=t:4,BD:BO=t:4,∴AC:AO=BD:BO,即CD∥AB,∵EF⊥CD,∴EF⊥AB.(2)
同课章节目录
