中考培优第二轮复习专题 第2章 火眼辨垂直学案(含答案)
文档属性
| 名称 | 中考培优第二轮复习专题 第2章 火眼辨垂直学案(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 00:00:00 | ||
图片预览





文档简介
第二章 火眼辨垂直
垂直自然可以与90°划上等号,所以找垂直就相当于找90°.
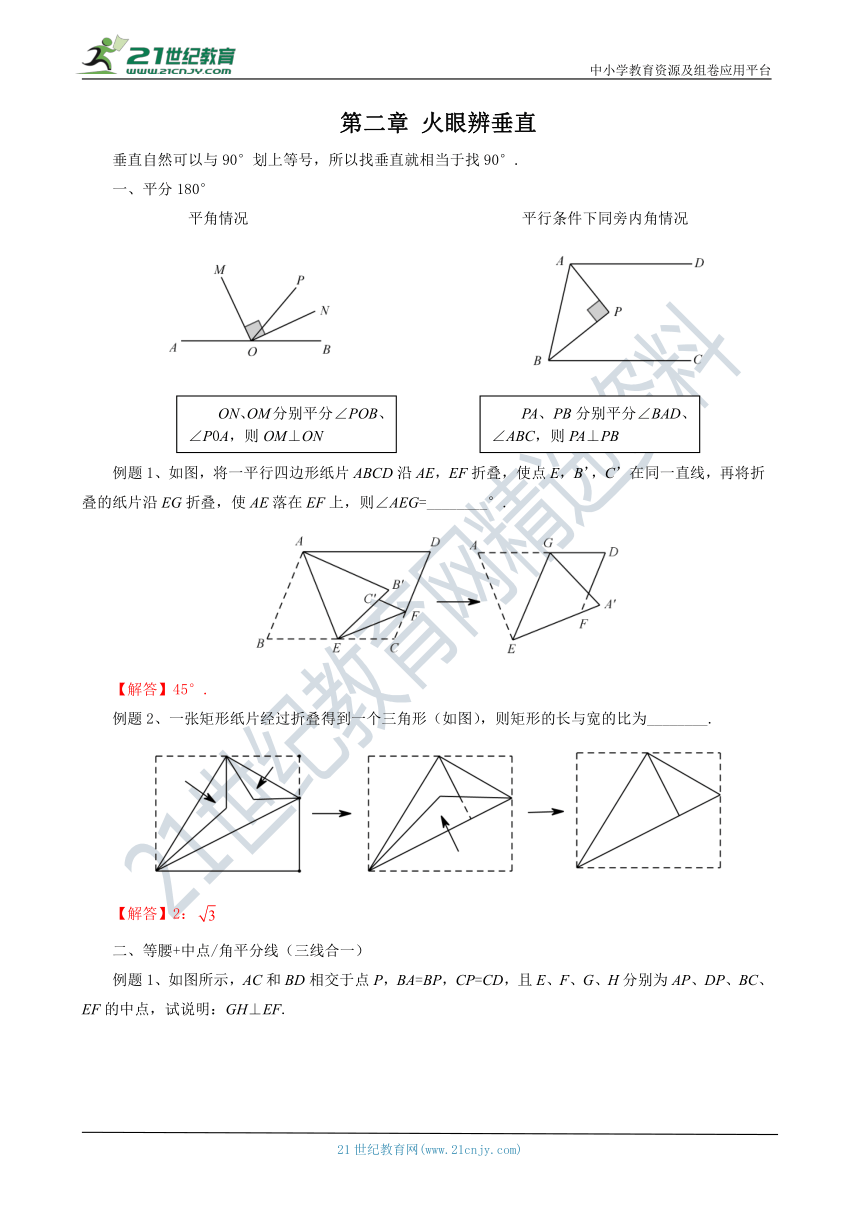
一、平分180°
平角情况 平行条件下同旁内角情况
例题1、如图,将一平行四边形纸片ABCD沿AE,EF折叠,使点E,B’,C’在同一直线,再将折叠的纸片沿EG折叠,使AE落在EF上,则∠AEG=________°.
【解答】45°.
例题2、一张矩形纸片经过折叠得到一个三角形(如图),则矩形的长与宽的比为________.
【解答】2:
二、等腰+中点/角平分线(三线合一)
例题1、如图所示,AC和BD相交于点P,BA=BP,CP=CD,且E、F、G、H分别为AP、DP、BC、EF的中点,试说明:GH⊥EF.
【解答】连接线段BE,EG,GF,FC.∵BA=BP,CP=CD,E、F分别是AP、PD的中点,∴BE⊥AP,CF⊥PD(三线合一),又∵G为BC的中点,∴EG=,FG=,∴EG=FG.又∵H为EF的中点,∴GH⊥EF.
三、暗藏勾股
例题1、如图,□ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=,AC=2,BD=4,则AE的长为________.
【解答】.
例题2、蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设AB边如图所示,C为格点,则△ABC是直角三角形的个数有________.
【解答】10个.
例题3、如图,抛物线交x轴于A(-3,0)、B(1,0)两点,交y轴于点C.
(1)求p、q的值;
(2)设抛物线的顶点为点D,连接AC、AD、CD,试探究:在坐标轴上是否存在这样的点P,使得以P、B、C为顶点的三角形与△ACD相似?若存在,请指出符合条件的点P的位置,并直接写出点P的坐标;若不存在,请说明理由.
【解答】解:(1)把A(﹣3,0)、B(1,0)代入,得,解得,∴抛物线的解析式为y=x2+2x﹣3;
(2)连接AC,易得:CD=,AC=3,AD=2,∴CD2+CA2=AD2,①计算可知Rt△COB∽Rt△ACD,得符合条件的点为O(0,0);②过B作BP2⊥BC交y轴正半轴于P2,可知Rt△CBP1∽Rt△COB∽Rt△ACD,求得符合条件的点为P2(0,);③过C作CP3⊥BC交x轴负半轴于P3,可知Rt△P2CB∽Rt△COB∽Rt△ACD,求得符合条件的点为P3(-9,0).∴符合条件的点有三个:(0,0),P2(0,),P2(-9,0).
四、一次函数的“k”互为负倒数
已知:,:,若,则.
例题1、在平面直角坐标系中,直线与x轴交于点A,与x轴交于点B,与交于点P,连接OP,当AB=20P时,b的值为________.
【解答】.
五、菱形对角线
例题1、如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50,则菱形的边长为________cm.
【解答】13.
例题2、如图,菱形ABCD的对角线相交于点E,以AD为斜边向上作等腰Rt△AFD,AF=FD,已知AD=2,∠BAD=120°,则EF的长为________.
【解答】.
六、有直径
例题1、平面直角坐标系中,点A、B的坐标分别为(4,0)、(0,4),点D为0B上任意一点,连接AD,以OD为直径的圆交AD于点E,则线段BE的最小值为________,此时E的坐标为________.
【解答】解:如图,∵OD是直径,∴∠OED=∠OEA=90°,∴点E的运动轨迹是以OA为直径的圆,设OA的中点为K,连接BK,当点E在BK上时,BE的长最短,∵A(4,0)、B(0,4),∴OA=PB=4,∵OK=KA=2,∴EK=OA=2,BK==2,∴BE的最小值为.
作EH⊥OA于H,∵EH∥OB,∴,∴,∴EH=,KH=,∴OH=2﹣,∴E(2﹣,).
例题2、如图,在△ABC,AB=AC,以AB为直径的圆分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠CAB.
(1)求证:直线BF是圆O的切线;
(2)若AB=5,sin∠CBF=,求BC和BF的长.
【解答】(1)证明:连接AE,∵AB是⊙O的直径,∴∠AEB=90°,∴∠1+∠2=90°.∵AB=AC,
∴∠1=∠CAB.∵∠CBF=∠CAB,∴∠1=∠CBF,∴∠CBF+∠2=90°,即∠ABF=90°,∵AB是⊙O的直径,∴直线BF是⊙O的切线.
(2)解:过点C作CG⊥AB于G.∵sin∠CBF=,∠1=∠CBF,∴sin∠1=,∵在Rt△AEB中,∠AEB=90°,AB=5,∴BE=AB?sin∠1=,∵AB=AC,∠AEB=90°,∴BC=2BE=2,
在Rt△ABE中,由勾股定理得AE==2,∴sin∠2=,cos∠2=,在Rt△CBG中,可求得GC=4,GB=2,∴AG=3,∵GC∥BF,∴△AGC∽△ABF,∴,∴BF=.
七、弦+中点(本质上还是三线合一)
例题1、已知“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1,在△ABC中,点D为BC的中点,有AB2+AC2=2AD2+2BD2.利用该结论解决以下问题:如图2,圆O的半径为6,点A在圆内,且OA=,点B和点C在圆O上,且∠BAC=90°,点E、F分别为A0、BC的中点,则EF的长为________;
【解答】4.
例题2、如图,AB为直径,AB=4,C、D为圆上两个动点,M为CD中点,DN⊥AB于N,∠DNM=30°,连接AD、AC,E、F分别为AC、AD的中点,连接EF,则EF的长为________.
【解答】EF=1.
八、相切有垂直(遇相切连圆心,百年不变)
例题1、如图,点A、B、D均在圆上,过点B作圆的切线BC,求证:∠BAD=∠DBC.
【解答】如图,连接BO并延长与圆O交于点E,连接DE,∵BC是圆O的切线,∴BE⊥BC,∴∠DBC+∠DBE=90°,又∵BE为直径,∴∠E+∠EBD=90°,∴∠E=∠DBE,∴∠A=∠DBC.
例题2、在直角坐标系中,点A的坐标为(3,0),点B是y轴正半轴上的一点,点C是第一象限内一点,且AC=2,设tan∠BOC=m,则m的最小值是________.
【解答】.
例题3、如图:已知菱形ABCD中,对角线AC和BD相交于点O,AC=8,BD=6,动点P在边AB上运动,以点O为圆心,OP为半径作O0,CQ切圆O于点Q.则在点P运动过程中,切线CQ的长的最大值为________.
【解答】.
九、全等或相似导角
例题1、如图,正方形ABCD中,AB=4cm,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,连接AF、BE相交于点P,点E、F运动的速度均为1cm/s,当它们到达各自终点时停止运动,设运动时间为t,当t=2s时,CP的长为________.
【解答】4.
例题2、如图,已知抛物线(其中)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
(1)求抛物线的关系式;
(2)过点M(1,0)的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
【解答】解:(1)当y=0时,﹣(x+1)(x﹣b)=0,解得x1=﹣1,x2=b,则A(﹣1,0)、B(b,0);抛物线的对称轴为直线x=,则D(,0)当x=0时,y=﹣(x+1)(x﹣b)=b,则C(0,b),∵点D恰好在线段BC的垂直平分线上.∴MC=MB,即b2+()2=(b﹣)2,解得b1=4,b2=0(舍去),∴抛物线的解析式为y=﹣(x+1)(x﹣4),即y=﹣x2+x+2;
(2)连接CN,如图,抛物线的对称轴为直线x=,则D(,0),当x=1时,y=﹣x2+x+2=3,则N(1,3),∴CN2=12+(3﹣2)2=2,CB2=22+42=20,BN2=(4﹣1)2+(3﹣0)2=18,∴BC2=CN2+BN2,∴△BCN为直角三角形,∠CNB=90°,∵BM=MN=3,∴∠MNB=∠MBN,∵∠BED=∠MNB﹣∠ACO,而∠ACO=∠CBO,∴∠BED=∠MBN﹣∠CBO=∠CBN,∴Rt△BED∽Rt△CBN,
∴,即,∴DE=,∴点E坐标为(,)或(,﹣).
十、双子型得定角(本模型出现在上册第三章)
例题1、如图,∠BAC=90°,△ABC绕点A逆时针旋转得△ADE,恰好点D在BC上,连接CE,求证:BC⊥CE.
【解答】由旋转的性质知:AB=AD,AC=AE,∠BAD=∠CAE;即∠ADB=∠B=(180°-∠BAD),∠ACE=∠AEC=(180°-∠CAE),即∠ADB=∠ACE=∠B=∠AEC,∴∠ACE+∠ACB=∠ACB+∠B=90°,∴BC⊥CE.
例题2、如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,点D为BC边上一点,且满足△ABC∽△ADE,取DE的中点F,连接CF,则CF的最小值为________.
【解答】4.
即时练习
1、如图,在△ABC中,∠ACB=90°,AB=18,cosB=,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为________.
【解答】.
十一、翻折
例题1、如图,在Rt△ABC中,∠C=90°,AC≠BC,点M是边AC上的动点.过点M作MN∥AB交BC于N,现将△MNC沿MN折叠,得到△MNP.若点P在AB上.则以MN为直径的圆与直线AB是何位置关系,试说明理由?
【解答】如图,连接PC交MN于点D,取MN的中点O,连接OP,由题意PD<OP,∴.圆心O到直线AB的距离小于圆O的半径,∴以MN为直径的圆与直线AB相交.
例题2、(2017·江阴区域二模)如图,将正方形ABCD的一角折向边CD,使点A与CB上一点E重合,若BE=1,CE=2,则折痕FG的长度为________.
【解答】.
垂直自然可以与90°划上等号,所以找垂直就相当于找90°.
一、平分180°
平角情况 平行条件下同旁内角情况
例题1、如图,将一平行四边形纸片ABCD沿AE,EF折叠,使点E,B’,C’在同一直线,再将折叠的纸片沿EG折叠,使AE落在EF上,则∠AEG=________°.
【解答】45°.
例题2、一张矩形纸片经过折叠得到一个三角形(如图),则矩形的长与宽的比为________.
【解答】2:
二、等腰+中点/角平分线(三线合一)
例题1、如图所示,AC和BD相交于点P,BA=BP,CP=CD,且E、F、G、H分别为AP、DP、BC、EF的中点,试说明:GH⊥EF.
【解答】连接线段BE,EG,GF,FC.∵BA=BP,CP=CD,E、F分别是AP、PD的中点,∴BE⊥AP,CF⊥PD(三线合一),又∵G为BC的中点,∴EG=,FG=,∴EG=FG.又∵H为EF的中点,∴GH⊥EF.
三、暗藏勾股
例题1、如图,□ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=,AC=2,BD=4,则AE的长为________.
【解答】.
例题2、蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设AB边如图所示,C为格点,则△ABC是直角三角形的个数有________.
【解答】10个.
例题3、如图,抛物线交x轴于A(-3,0)、B(1,0)两点,交y轴于点C.
(1)求p、q的值;
(2)设抛物线的顶点为点D,连接AC、AD、CD,试探究:在坐标轴上是否存在这样的点P,使得以P、B、C为顶点的三角形与△ACD相似?若存在,请指出符合条件的点P的位置,并直接写出点P的坐标;若不存在,请说明理由.
【解答】解:(1)把A(﹣3,0)、B(1,0)代入,得,解得,∴抛物线的解析式为y=x2+2x﹣3;
(2)连接AC,易得:CD=,AC=3,AD=2,∴CD2+CA2=AD2,①计算可知Rt△COB∽Rt△ACD,得符合条件的点为O(0,0);②过B作BP2⊥BC交y轴正半轴于P2,可知Rt△CBP1∽Rt△COB∽Rt△ACD,求得符合条件的点为P2(0,);③过C作CP3⊥BC交x轴负半轴于P3,可知Rt△P2CB∽Rt△COB∽Rt△ACD,求得符合条件的点为P3(-9,0).∴符合条件的点有三个:(0,0),P2(0,),P2(-9,0).
四、一次函数的“k”互为负倒数
已知:,:,若,则.
例题1、在平面直角坐标系中,直线与x轴交于点A,与x轴交于点B,与交于点P,连接OP,当AB=20P时,b的值为________.
【解答】.
五、菱形对角线
例题1、如图,菱形ABCD的面积为120cm2,正方形AECF的面积为50,则菱形的边长为________cm.
【解答】13.
例题2、如图,菱形ABCD的对角线相交于点E,以AD为斜边向上作等腰Rt△AFD,AF=FD,已知AD=2,∠BAD=120°,则EF的长为________.
【解答】.
六、有直径
例题1、平面直角坐标系中,点A、B的坐标分别为(4,0)、(0,4),点D为0B上任意一点,连接AD,以OD为直径的圆交AD于点E,则线段BE的最小值为________,此时E的坐标为________.
【解答】解:如图,∵OD是直径,∴∠OED=∠OEA=90°,∴点E的运动轨迹是以OA为直径的圆,设OA的中点为K,连接BK,当点E在BK上时,BE的长最短,∵A(4,0)、B(0,4),∴OA=PB=4,∵OK=KA=2,∴EK=OA=2,BK==2,∴BE的最小值为.
作EH⊥OA于H,∵EH∥OB,∴,∴,∴EH=,KH=,∴OH=2﹣,∴E(2﹣,).
例题2、如图,在△ABC,AB=AC,以AB为直径的圆分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=∠CAB.
(1)求证:直线BF是圆O的切线;
(2)若AB=5,sin∠CBF=,求BC和BF的长.
【解答】(1)证明:连接AE,∵AB是⊙O的直径,∴∠AEB=90°,∴∠1+∠2=90°.∵AB=AC,
∴∠1=∠CAB.∵∠CBF=∠CAB,∴∠1=∠CBF,∴∠CBF+∠2=90°,即∠ABF=90°,∵AB是⊙O的直径,∴直线BF是⊙O的切线.
(2)解:过点C作CG⊥AB于G.∵sin∠CBF=,∠1=∠CBF,∴sin∠1=,∵在Rt△AEB中,∠AEB=90°,AB=5,∴BE=AB?sin∠1=,∵AB=AC,∠AEB=90°,∴BC=2BE=2,
在Rt△ABE中,由勾股定理得AE==2,∴sin∠2=,cos∠2=,在Rt△CBG中,可求得GC=4,GB=2,∴AG=3,∵GC∥BF,∴△AGC∽△ABF,∴,∴BF=.
七、弦+中点(本质上还是三线合一)
例题1、已知“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1,在△ABC中,点D为BC的中点,有AB2+AC2=2AD2+2BD2.利用该结论解决以下问题:如图2,圆O的半径为6,点A在圆内,且OA=,点B和点C在圆O上,且∠BAC=90°,点E、F分别为A0、BC的中点,则EF的长为________;
【解答】4.
例题2、如图,AB为直径,AB=4,C、D为圆上两个动点,M为CD中点,DN⊥AB于N,∠DNM=30°,连接AD、AC,E、F分别为AC、AD的中点,连接EF,则EF的长为________.
【解答】EF=1.
八、相切有垂直(遇相切连圆心,百年不变)
例题1、如图,点A、B、D均在圆上,过点B作圆的切线BC,求证:∠BAD=∠DBC.
【解答】如图,连接BO并延长与圆O交于点E,连接DE,∵BC是圆O的切线,∴BE⊥BC,∴∠DBC+∠DBE=90°,又∵BE为直径,∴∠E+∠EBD=90°,∴∠E=∠DBE,∴∠A=∠DBC.
例题2、在直角坐标系中,点A的坐标为(3,0),点B是y轴正半轴上的一点,点C是第一象限内一点,且AC=2,设tan∠BOC=m,则m的最小值是________.
【解答】.
例题3、如图:已知菱形ABCD中,对角线AC和BD相交于点O,AC=8,BD=6,动点P在边AB上运动,以点O为圆心,OP为半径作O0,CQ切圆O于点Q.则在点P运动过程中,切线CQ的长的最大值为________.
【解答】.
九、全等或相似导角
例题1、如图,正方形ABCD中,AB=4cm,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,连接AF、BE相交于点P,点E、F运动的速度均为1cm/s,当它们到达各自终点时停止运动,设运动时间为t,当t=2s时,CP的长为________.
【解答】4.
例题2、如图,已知抛物线(其中)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
(1)求抛物线的关系式;
(2)过点M(1,0)的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
【解答】解:(1)当y=0时,﹣(x+1)(x﹣b)=0,解得x1=﹣1,x2=b,则A(﹣1,0)、B(b,0);抛物线的对称轴为直线x=,则D(,0)当x=0时,y=﹣(x+1)(x﹣b)=b,则C(0,b),∵点D恰好在线段BC的垂直平分线上.∴MC=MB,即b2+()2=(b﹣)2,解得b1=4,b2=0(舍去),∴抛物线的解析式为y=﹣(x+1)(x﹣4),即y=﹣x2+x+2;
(2)连接CN,如图,抛物线的对称轴为直线x=,则D(,0),当x=1时,y=﹣x2+x+2=3,则N(1,3),∴CN2=12+(3﹣2)2=2,CB2=22+42=20,BN2=(4﹣1)2+(3﹣0)2=18,∴BC2=CN2+BN2,∴△BCN为直角三角形,∠CNB=90°,∵BM=MN=3,∴∠MNB=∠MBN,∵∠BED=∠MNB﹣∠ACO,而∠ACO=∠CBO,∴∠BED=∠MBN﹣∠CBO=∠CBN,∴Rt△BED∽Rt△CBN,
∴,即,∴DE=,∴点E坐标为(,)或(,﹣).
十、双子型得定角(本模型出现在上册第三章)
例题1、如图,∠BAC=90°,△ABC绕点A逆时针旋转得△ADE,恰好点D在BC上,连接CE,求证:BC⊥CE.
【解答】由旋转的性质知:AB=AD,AC=AE,∠BAD=∠CAE;即∠ADB=∠B=(180°-∠BAD),∠ACE=∠AEC=(180°-∠CAE),即∠ADB=∠ACE=∠B=∠AEC,∴∠ACE+∠ACB=∠ACB+∠B=90°,∴BC⊥CE.
例题2、如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,点D为BC边上一点,且满足△ABC∽△ADE,取DE的中点F,连接CF,则CF的最小值为________.
【解答】4.
即时练习
1、如图,在△ABC中,∠ACB=90°,AB=18,cosB=,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为________.
【解答】.
十一、翻折
例题1、如图,在Rt△ABC中,∠C=90°,AC≠BC,点M是边AC上的动点.过点M作MN∥AB交BC于N,现将△MNC沿MN折叠,得到△MNP.若点P在AB上.则以MN为直径的圆与直线AB是何位置关系,试说明理由?
【解答】如图,连接PC交MN于点D,取MN的中点O,连接OP,由题意PD<OP,∴.圆心O到直线AB的距离小于圆O的半径,∴以MN为直径的圆与直线AB相交.
例题2、(2017·江阴区域二模)如图,将正方形ABCD的一角折向边CD,使点A与CB上一点E重合,若BE=1,CE=2,则折痕FG的长度为________.
【解答】.
同课章节目录
