中考培优第二轮复习专题 第3章 网格作图学案(含答案)
文档属性
| 名称 | 中考培优第二轮复习专题 第3章 网格作图学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 12:07:46 | ||
图片预览


文档简介
第三章 网格作图
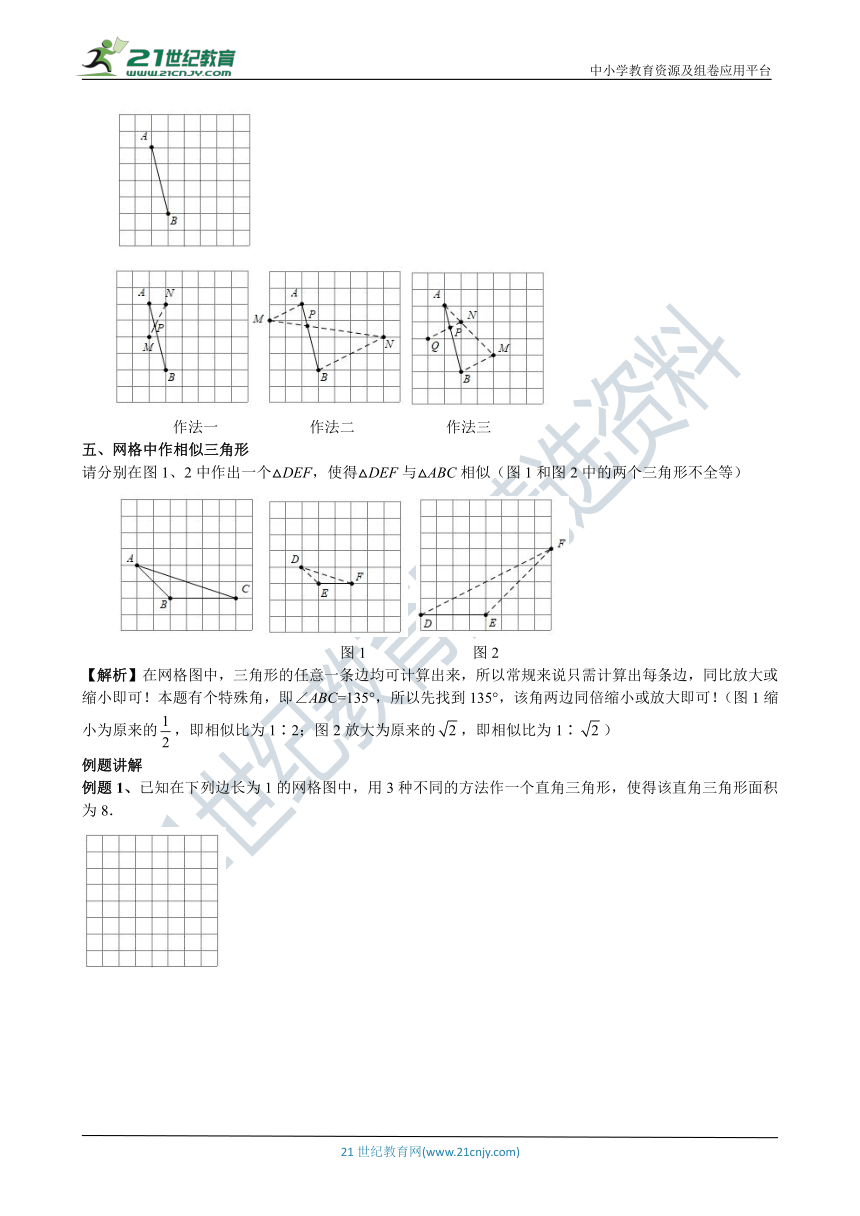
网格作图的特点:仅利用无刻度直尺,利用格点来作图,所以在网格中作图时一定要体现出过的格点.
基本知识
一、网格中作平行
图1 图2
图1中虚线线段均与线段AB平行,仔细观察,可发现线段AB长宽比为3∶1的矩形对角线,故想要作出与AB线段平行的线,必然也要使得作出的线段是长宽比为3∶1的矩形对角线,所以图1、图2均满足要求,即都与AB平行.
二、网格中作垂直
图1
图1中虚线线段均与线段AB垂直,仔细观察,可发现线段AB长宽比为3∶1的矩形对角线,故想要作出与AB线段垂直的线,必然也要使得作出的线段是长宽比为3∶1的矩形对角线.【与平行的区别在于一个竖方向,一个横方向】
三、网格中作垂直平分线
在网格中垂直平分线的做法,利用垂直平分线性质逆定理,首先需要找到线段A、B两点距离相等的格点,图1中的C、D、E均满足到A、B距离相等,故连接CE(或者ED或者CD均可).此方法也适用于在网格中作线段中点,如图2
图1 图2
四、网格中等分线段
以作三等分为例,在下列网格中,在线段AB上找一点P,使得BP=2AP.此类作图可利用相似的性质来解决,以下示范3种作法
作法一 作法二 作法三
五、网格中作相似三角形
请分别在图1、2中作出一个△DEF,使得△DEF与△ABC相似(图1和图2中的两个三角形不全等)
图1 图2
【解析】在网格图中,三角形的任意一条边均可计算出来,所以常规来说只需计算出每条边,同比放大或缩小即可!本题有个特殊角,即∠ABC=135°,所以先找到135°,该角两边同倍缩小或放大即可!(图1缩小为原来的,即相似比为1∶2;图2放大为原来的,即相似比为1∶)
例题讲解
例题1、已知在下列边长为1的网格图中,用3种不同的方法作一个直角三角形,使得该直角三角形面积为8.
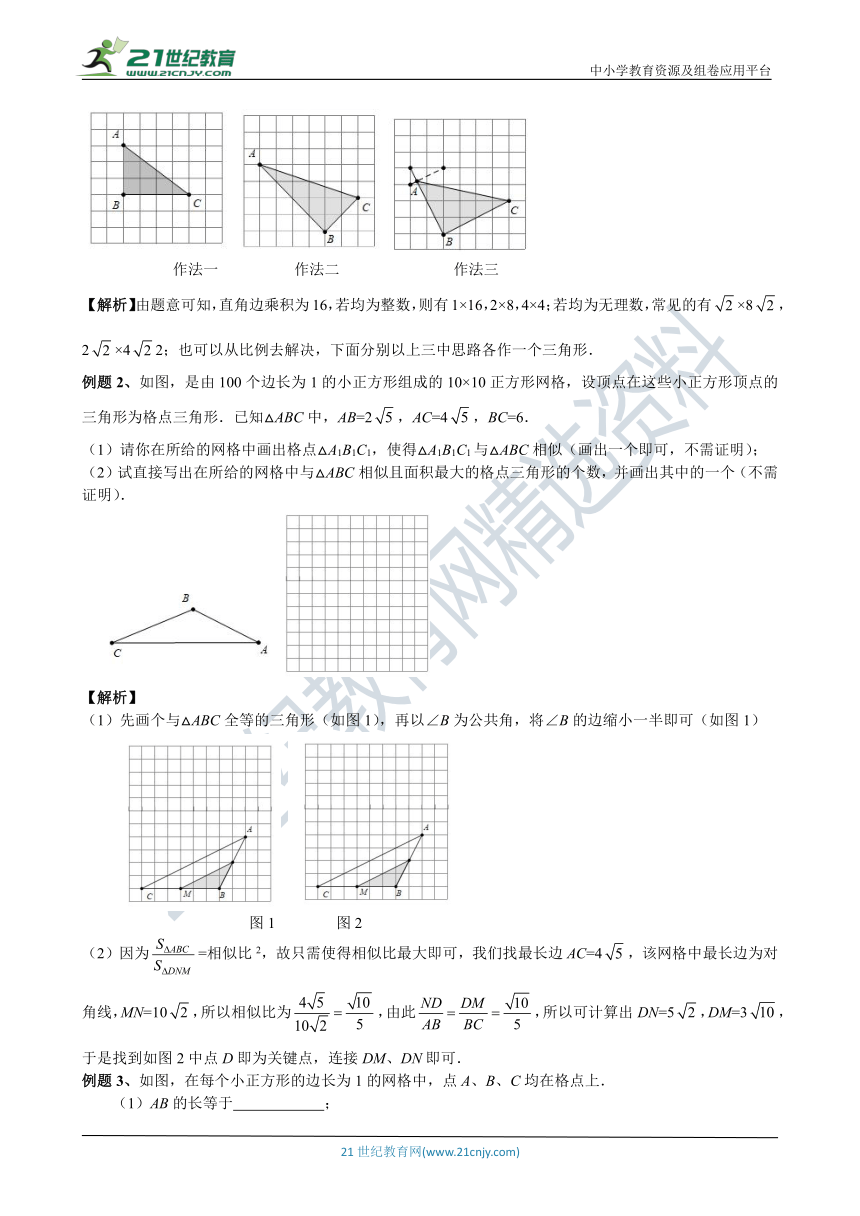
作法一 作法二 作法三
【解析】由题意可知,直角边乘积为16,若均为整数,则有1×16,2×8,4×4;若均为无理数,常见的有×8,2×42;也可以从比例去解决,下面分别以上三中思路各作一个三角形.
例题2、如图,是由100个边长为1的小正方形组成的10×10正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形.已知△ABC中,AB=2,AC=4,BC=6.
(1)请你在所给的网格中画出格点△A1B1C1,使得△A1B1C1与△ABC相似(画出一个即可,不需证明);
(2)试直接写出在所给的网格中与△ABC相似且面积最大的格点三角形的个数,并画出其中的一个(不需证明).
【解析】
(1)先画个与△ABC全等的三角形(如图1),再以∠B为公共角,将∠B的边缩小一半即可(如图1)
图1 图2
(2)因为=相似比2,故只需使得相似比最大即可,我们找最长边AC=4,该网格中最长边为对角线,MN=10,所以相似比为,由此,所以可计算出DN=5,DM=3,于是找到如图2中点D即为关键点,连接DM、DN即可.
例题3、如图,在每个小正方形的边长为1的网格中,点A、B、C均在格点上.
(1)AB的长等于 ;
(2)在△ABC的内部有一点P,满足S△PAB∶S△PBC∶S△PCA=1∶2∶3,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明).
【解析】
(1)AB=;
(2)方法一:关注到S△PAB+S△PBC=S△PCA,可得到S△PCA =S△ABC.如图1,找到AB中点D,过点D作AC平行线,交BC与点E,所以点P必然在线段DE上.在网格中找到一点M,使得点C到MB的距离与点A到MB的距离之比为1∶2.如图2,点Q为AC三等分点,连接BO,与线段DE交点即为点P.
方法二:发现AC边上本身就存在点D、E使得AD:EC:DE=1∶2∶3,先作出如下图形,接着利用平行,将△ADB和△BEC面积转化.
过点B作AC平行线,与l1交于点H,与l2交于点G,连接EG、DH,易证EG∥BC,DH∥AB,所以EG与DH交点即为点P.
巩固练习
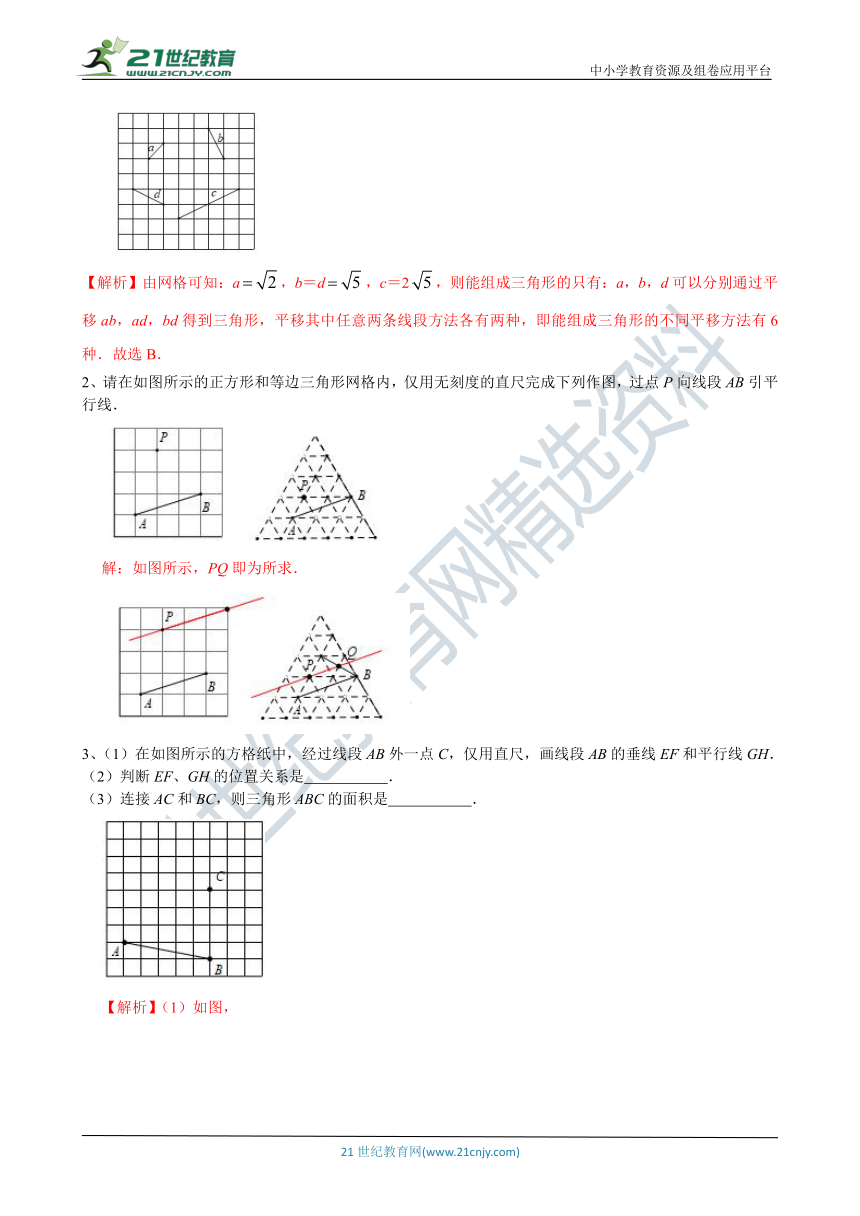
1、如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有( )
A.3种 B. 6种 C.8种 D.12种
【解析】由网格可知:a,b=d,c=2,则能组成三角形的只有:a,b,d可以分别通过平移ab,ad,bd得到三角形,平移其中任意两条线段方法各有两种,即能组成三角形的不同平移方法有6种.故选B.
2、请在如图所示的正方形和等边三角形网格内,仅用无刻度的直尺完成下列作图,过点P向线段AB引平行线.
解:如图所示,PQ即为所求.
3、(1)在如图所示的方格纸中,经过线段AB外一点C,仅用直尺,画线段AB的垂线EF和平行线GH.
(2)判断EF、GH的位置关系是 .
(3)连接AC和BC,则三角形ABC的面积是 .
【解析】(1)如图,
(2)EF、GH的位置关系是EF⊥GH,故答案为EF⊥GH.
(3)如图,连接AC和BC,设小方格的边长为1,则三角形ABC的面积是4×5=10.故答案为10.
4、如图,方格图中每个小格的边长为1,仅用直尺过点C画线段CD,使CD∥AB,D是格点,过C作AB的垂线CH,垂足为H.连结BC、AD.
(1)试猜想:线段BC与线段AD的关系为 ;
(2)请计算:四边形ABCD的面积为 ;
(3)若线段AB的长为m,则线段CH长度为 .(用含m的代数式表示)
解:(1)∵AD=BC,∴BC∥AD且BC=AD.故答案为BC∥AD且BC=AD;
(2)S?ABCD=3×51×21×41×21×4=15﹣1﹣2﹣1﹣2=9.故答案为9;
(3)∵ABm,S?ABCD=9m,∴AB?CH=9,即CHmm.故答案为m.
5、(1)在如图所示的方格纸中,点P是∠AOB的边OB上的一点,不用量角器与三角尺,仅用直尺,完成下列各题:
①过点P画OB的垂线,交OA于点C;②过点P画OA的垂线,垂足为H;
(2)在上图中线段PH的长度是点P到直线 的距离, 线段 的长度是点C到直线OB的距离.PC、PH、OC这三条线段大小关系是 .(用“<”号连接)
解:(1)如图,直线PK,PH即为所求;
(2)线段PH的长度是点P到直线OA的距离;线段CP的长度是点C到直线OB的距离;H<PC<CO.
6、在数学活动课上,老师要求学生在5×5的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB或AD都不平行.画四种图形,并直接写出其周长(所画图象相似的只算一种).
图1 图2 图3 图4
解:如图1,三角形的周长=2;
如图2,三角形的周长=42;
如图3,三角形的周长=5;
如图4,三角形的周长=3.
图1 图2 图3 图4
7、图1,图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.
(1)在图1中画出等腰直角△MON,使点N在格点上,且∠MON=90°;
(2)在图2中以格点为顶点画出一个正方形ABCD,使正方形ABCD面积等于(1)中等腰直角△MON面积的4倍,并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形,且正方形ABCD面积没有剩余(画出一种即可).
图1 图2
解:(1)如图1所示:∠MON=90°;
图1 图2 图3
(2)如图2、3所示.
8、如图,△ABC是正方形网格中的格点三角形(顶点在格点上),请在正方形网格上按下列要求画一个格点三角形与△ABC相似.
(1)在图1中画△AlB1C1,使得△AlB1C1的周长是△ABC的周长的2倍;
(2)在图2中画出△A2B2C2,使得△A2B2C2的面积是△ABC的面积的2倍.
图1 图2
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求.
图1 图2
9、在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,—4),B(3,—2),C(6,—3)
(1)画出△ABC关于x轴对称的△AlB1C1;
(2)以M点为位似中心,在网格中画出△AlB1C1的位似图形△A2B4C2,使△A2B2C2与△AlB1C1的相似比为2∶1.
(3)求出A2、B2、C2三点的坐标.
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)△A2B2C2的面积为:4×82×42×62×8=14.故答案为14.
10、如图,将线段AB放在边长为1的小正方形网格,点A点B均落在格点上,请用无刻度直尺在线段AB上画出点P,使AP=,并保留作图痕迹.(备注:本题只是找点不是证明,所以只需连接一对角线就行)
解:由勾股定理得,AB,所以,AP时AP∶BP=2∶1.点P如图所示.
11、如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置;
(2)点M的坐标为 ;
(3)判断点D(5,—2)与OM的位置关系.
(3)判断点D(5,﹣2)与⊙M的位置关系.
解:(1)如图1,点M就是要找的圆心;
(2)圆心M的坐标为(2,0).故答案为(2,0);
(3)圆的半径AM2.
线段MD2,
所以点D在⊙M内.
12、如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.
(1)画出该圆弧所在圆的圆心D的位置(不用写作法,保留作图痕迹),并连接AD、CD.
(2)请在(1)的基础上,以点0为原点、水平方向所在直线为x轴、竖直方向所在直线为y轴,建立平面直角坐标系,完成下列问题:
①OD的半径为(结果保留根号);
②若用扇形ADC围成一个圆锥的侧面,则该圆锥的底面圆半径是;
③若E(7,0),试判断直线EC与⊙D的位置关系并说明你的理由.
解:(1)根据题意画出相应的图形,如图所示:
(2)①在Rt△AOD中,OA=4,OD=2,根据勾股定理得:AD2,则⊙D的半径为2;
②AC2,CD=2,AD2+CD2=AC2,∴∠ADC=90°.
扇形ADC的弧长π,圆锥的底面的半径;
③直线EC与⊙D的位置关系为相切,理由为:在Rt△CEF中,CF=2,EF=1,根据勾股定理得:CE,
在△CDE中,CD=2,CE,DE=5,∵CE2+CD2=()2+(2)2=5+20=25,DE2=25,∴CE2+CD2=DE2,∴△CDE为直角三角形,即∠DCE=90°,则CE与圆D相切.
网格作图的特点:仅利用无刻度直尺,利用格点来作图,所以在网格中作图时一定要体现出过的格点.
基本知识
一、网格中作平行
图1 图2
图1中虚线线段均与线段AB平行,仔细观察,可发现线段AB长宽比为3∶1的矩形对角线,故想要作出与AB线段平行的线,必然也要使得作出的线段是长宽比为3∶1的矩形对角线,所以图1、图2均满足要求,即都与AB平行.
二、网格中作垂直
图1
图1中虚线线段均与线段AB垂直,仔细观察,可发现线段AB长宽比为3∶1的矩形对角线,故想要作出与AB线段垂直的线,必然也要使得作出的线段是长宽比为3∶1的矩形对角线.【与平行的区别在于一个竖方向,一个横方向】
三、网格中作垂直平分线
在网格中垂直平分线的做法,利用垂直平分线性质逆定理,首先需要找到线段A、B两点距离相等的格点,图1中的C、D、E均满足到A、B距离相等,故连接CE(或者ED或者CD均可).此方法也适用于在网格中作线段中点,如图2
图1 图2
四、网格中等分线段
以作三等分为例,在下列网格中,在线段AB上找一点P,使得BP=2AP.此类作图可利用相似的性质来解决,以下示范3种作法
作法一 作法二 作法三
五、网格中作相似三角形
请分别在图1、2中作出一个△DEF,使得△DEF与△ABC相似(图1和图2中的两个三角形不全等)
图1 图2
【解析】在网格图中,三角形的任意一条边均可计算出来,所以常规来说只需计算出每条边,同比放大或缩小即可!本题有个特殊角,即∠ABC=135°,所以先找到135°,该角两边同倍缩小或放大即可!(图1缩小为原来的,即相似比为1∶2;图2放大为原来的,即相似比为1∶)
例题讲解
例题1、已知在下列边长为1的网格图中,用3种不同的方法作一个直角三角形,使得该直角三角形面积为8.
作法一 作法二 作法三
【解析】由题意可知,直角边乘积为16,若均为整数,则有1×16,2×8,4×4;若均为无理数,常见的有×8,2×42;也可以从比例去解决,下面分别以上三中思路各作一个三角形.
例题2、如图,是由100个边长为1的小正方形组成的10×10正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形.已知△ABC中,AB=2,AC=4,BC=6.
(1)请你在所给的网格中画出格点△A1B1C1,使得△A1B1C1与△ABC相似(画出一个即可,不需证明);
(2)试直接写出在所给的网格中与△ABC相似且面积最大的格点三角形的个数,并画出其中的一个(不需证明).
【解析】
(1)先画个与△ABC全等的三角形(如图1),再以∠B为公共角,将∠B的边缩小一半即可(如图1)
图1 图2
(2)因为=相似比2,故只需使得相似比最大即可,我们找最长边AC=4,该网格中最长边为对角线,MN=10,所以相似比为,由此,所以可计算出DN=5,DM=3,于是找到如图2中点D即为关键点,连接DM、DN即可.
例题3、如图,在每个小正方形的边长为1的网格中,点A、B、C均在格点上.
(1)AB的长等于 ;
(2)在△ABC的内部有一点P,满足S△PAB∶S△PBC∶S△PCA=1∶2∶3,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明).
【解析】
(1)AB=;
(2)方法一:关注到S△PAB+S△PBC=S△PCA,可得到S△PCA =S△ABC.如图1,找到AB中点D,过点D作AC平行线,交BC与点E,所以点P必然在线段DE上.在网格中找到一点M,使得点C到MB的距离与点A到MB的距离之比为1∶2.如图2,点Q为AC三等分点,连接BO,与线段DE交点即为点P.
方法二:发现AC边上本身就存在点D、E使得AD:EC:DE=1∶2∶3,先作出如下图形,接着利用平行,将△ADB和△BEC面积转化.
过点B作AC平行线,与l1交于点H,与l2交于点G,连接EG、DH,易证EG∥BC,DH∥AB,所以EG与DH交点即为点P.
巩固练习
1、如图,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有( )
A.3种 B. 6种 C.8种 D.12种
【解析】由网格可知:a,b=d,c=2,则能组成三角形的只有:a,b,d可以分别通过平移ab,ad,bd得到三角形,平移其中任意两条线段方法各有两种,即能组成三角形的不同平移方法有6种.故选B.
2、请在如图所示的正方形和等边三角形网格内,仅用无刻度的直尺完成下列作图,过点P向线段AB引平行线.
解:如图所示,PQ即为所求.
3、(1)在如图所示的方格纸中,经过线段AB外一点C,仅用直尺,画线段AB的垂线EF和平行线GH.
(2)判断EF、GH的位置关系是 .
(3)连接AC和BC,则三角形ABC的面积是 .
【解析】(1)如图,
(2)EF、GH的位置关系是EF⊥GH,故答案为EF⊥GH.
(3)如图,连接AC和BC,设小方格的边长为1,则三角形ABC的面积是4×5=10.故答案为10.
4、如图,方格图中每个小格的边长为1,仅用直尺过点C画线段CD,使CD∥AB,D是格点,过C作AB的垂线CH,垂足为H.连结BC、AD.
(1)试猜想:线段BC与线段AD的关系为 ;
(2)请计算:四边形ABCD的面积为 ;
(3)若线段AB的长为m,则线段CH长度为 .(用含m的代数式表示)
解:(1)∵AD=BC,∴BC∥AD且BC=AD.故答案为BC∥AD且BC=AD;
(2)S?ABCD=3×51×21×41×21×4=15﹣1﹣2﹣1﹣2=9.故答案为9;
(3)∵ABm,S?ABCD=9m,∴AB?CH=9,即CHmm.故答案为m.
5、(1)在如图所示的方格纸中,点P是∠AOB的边OB上的一点,不用量角器与三角尺,仅用直尺,完成下列各题:
①过点P画OB的垂线,交OA于点C;②过点P画OA的垂线,垂足为H;
(2)在上图中线段PH的长度是点P到直线 的距离, 线段 的长度是点C到直线OB的距离.PC、PH、OC这三条线段大小关系是 .(用“<”号连接)
解:(1)如图,直线PK,PH即为所求;
(2)线段PH的长度是点P到直线OA的距离;线段CP的长度是点C到直线OB的距离;H<PC<CO.
6、在数学活动课上,老师要求学生在5×5的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB或AD都不平行.画四种图形,并直接写出其周长(所画图象相似的只算一种).
图1 图2 图3 图4
解:如图1,三角形的周长=2;
如图2,三角形的周长=42;
如图3,三角形的周长=5;
如图4,三角形的周长=3.
图1 图2 图3 图4
7、图1,图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.
(1)在图1中画出等腰直角△MON,使点N在格点上,且∠MON=90°;
(2)在图2中以格点为顶点画出一个正方形ABCD,使正方形ABCD面积等于(1)中等腰直角△MON面积的4倍,并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形,且正方形ABCD面积没有剩余(画出一种即可).
图1 图2
解:(1)如图1所示:∠MON=90°;
图1 图2 图3
(2)如图2、3所示.
8、如图,△ABC是正方形网格中的格点三角形(顶点在格点上),请在正方形网格上按下列要求画一个格点三角形与△ABC相似.
(1)在图1中画△AlB1C1,使得△AlB1C1的周长是△ABC的周长的2倍;
(2)在图2中画出△A2B2C2,使得△A2B2C2的面积是△ABC的面积的2倍.
图1 图2
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求.
图1 图2
9、在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,—4),B(3,—2),C(6,—3)
(1)画出△ABC关于x轴对称的△AlB1C1;
(2)以M点为位似中心,在网格中画出△AlB1C1的位似图形△A2B4C2,使△A2B2C2与△AlB1C1的相似比为2∶1.
(3)求出A2、B2、C2三点的坐标.
解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)△A2B2C2的面积为:4×82×42×62×8=14.故答案为14.
10、如图,将线段AB放在边长为1的小正方形网格,点A点B均落在格点上,请用无刻度直尺在线段AB上画出点P,使AP=,并保留作图痕迹.(备注:本题只是找点不是证明,所以只需连接一对角线就行)
解:由勾股定理得,AB,所以,AP时AP∶BP=2∶1.点P如图所示.
11、如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)在图中画出经过A、B、C三点的圆弧所在圆的圆心M的位置;
(2)点M的坐标为 ;
(3)判断点D(5,—2)与OM的位置关系.
(3)判断点D(5,﹣2)与⊙M的位置关系.
解:(1)如图1,点M就是要找的圆心;
(2)圆心M的坐标为(2,0).故答案为(2,0);
(3)圆的半径AM2.
线段MD2,
所以点D在⊙M内.
12、如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.
(1)画出该圆弧所在圆的圆心D的位置(不用写作法,保留作图痕迹),并连接AD、CD.
(2)请在(1)的基础上,以点0为原点、水平方向所在直线为x轴、竖直方向所在直线为y轴,建立平面直角坐标系,完成下列问题:
①OD的半径为(结果保留根号);
②若用扇形ADC围成一个圆锥的侧面,则该圆锥的底面圆半径是;
③若E(7,0),试判断直线EC与⊙D的位置关系并说明你的理由.
解:(1)根据题意画出相应的图形,如图所示:
(2)①在Rt△AOD中,OA=4,OD=2,根据勾股定理得:AD2,则⊙D的半径为2;
②AC2,CD=2,AD2+CD2=AC2,∴∠ADC=90°.
扇形ADC的弧长π,圆锥的底面的半径;
③直线EC与⊙D的位置关系为相切,理由为:在Rt△CEF中,CF=2,EF=1,根据勾股定理得:CE,
在△CDE中,CD=2,CE,DE=5,∵CE2+CD2=()2+(2)2=5+20=25,DE2=25,∴CE2+CD2=DE2,∴△CDE为直角三角形,即∠DCE=90°,则CE与圆D相切.
同课章节目录
