中考培优第二轮复习专题 第4章 网格内求解三角函数值学案(含答案)
文档属性
| 名称 | 中考培优第二轮复习专题 第4章 网格内求解三角函数值学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 12:11:10 | ||
图片预览



文档简介
第四章 网格内求解三角函数值
网格内的图形特点:为格点图形,则边长均可求;若不是格点图形,多边形内角可转换.
例题讲解
一、构造直角
例题1、网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则sinA= .
【解析】如图,作AD⊥BC于D,CE⊥AB于E,由勾股定理得AB=AC=2,BC=2,AD=3,可以得知△ABC是等腰三角形,由面积相等可得,BC?ADAB?CE,
即CE,sinA,故答案为.
【总结】由于格点三角形各边都可求,所以利用解直角三角形即可求出各个内角的三角函数值.
二、角度转换
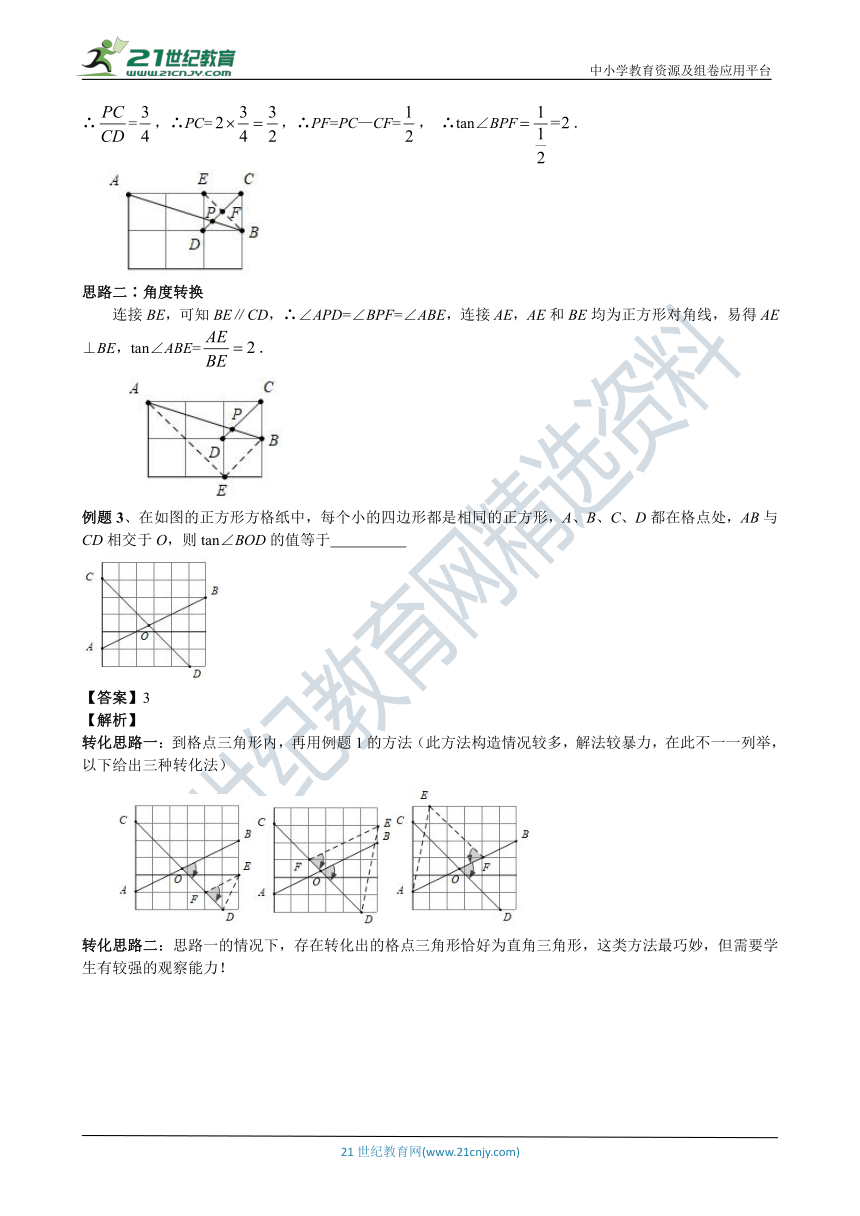
例题2、如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是 .
思路一:构造直角
连接BE,由四边形EDBC为正方形可知,CD⊥BE,∴tan∠APD=tan∠BPF=,设小正方形边长为(思考一下为什么可以这么设?),可得BF=1,CD=2,由△ACP∽△BDP,且相似比为3∶1可得=3,∴=,∴PC=,∴PF=PC—CF=, ∴tan∠BPF.
思路二∶角度转换
连接BE,可知BE∥CD,∴∠APD=∠BPF=∠ABE,连接AE,AE和BE均为正方形对角线,易得AE⊥BE,tan∠ABE=.
例题3、在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A、B、C、D都在格点处,AB与CD相交于O,则tan∠BOD的值等于
【答案】3
【解析】
转化思路一:到格点三角形内,再用例题1的方法(此方法构造情况较多,解法较暴力,在此不一一列举,以下给出三种转化法)
转化思路二:思路一的情况下,存在转化出的格点三角形恰好为直角三角形,这类方法最巧妙,但需要学生有较强的观察能力!
直角构造思路三:通过连接某些辅助线,构造出直角后直接在直角三角形内求解.
巩固练习
1、如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是 .
【解析】连接AC,由网格特点和正方形的性质可知,∠BAC=90°,根据勾股定理得,AC,AB=2,则tan∠ABC,故答案为.
2、如图,在4x5的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则tan∠ABC= ;sin∠ACB= .
【解析】找到与A构成小正方形对角线的格点D、E,连接CD,AE,EB,AC与EB交于点F.由网格特点和正方形的性质可知,∠BAE=90°,根据勾股定理得,AE,AB=3,DB=2,DC=3,BE=,则tan∠ABC,又BE⊥AC,易得△AEF∽△BAF,故,∴,∴BF=,sin∠ACB=,故答案为3,.
3、如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则的值= ,tan∠APD的值= .
【解析】∵四边形BCED是正方形,∴DB∥AC,∴△DBP∽△CAP,∴3,
连接BE,∵四边形BCED是正方形,∴DF=CFCD,BFBE,CD=BE,BE⊥CD,∴BF=CF,根据题意得:AC∥BD,∴△ACP∽△BDP,∴DP:CP=BD:AC=1:3,
∴DP:DF=1:2,∴DP=PFCFBF,在Rt△PBF中,tan∠BPF2,
∵∠APD=∠BPF,∴tan∠APD=2,故答案为3,2.
4、如图,在正方形网格中,△ABC的顶点都在格点上,则tan∠ACB的值为 .
【解析】解:作AD⊥BC于D,由勾股定理得,AC,AB=3,BC=4,
△ABC的面积为:AB×CE=6,∴CB×AD=6,解得AD,
CD,tan∠ACB.故答案为.
5、如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是 .
【解析】如图,连接EA,EC,设菱形的边长为a,由题意得∠AEF=30°,∠BEF=60°,AEa,EB=2a,∴∠AEC=90°,∵∠ACE=∠ACG=∠BCG=60°,
∴E、C、B共线,在Rt△AEB中,tan∠ABC.故答案为.
第5题
6、如图,网格中的四个格点组成菱形ABCD,则tan∠DBC的值为 .
【解析】如图,连接AC与BD相交于点O,∵四边形ABCD是菱形,∴AC⊥BD,BOBD,COAC,由勾股定理得,AC3,BD,所以,BO,CO3,所以,tan∠DBC3.故答案为3.
7、如图1是由边长为1的小正方形组成的网格,点A、B、C、D都在网格的格点上,AC、BD相交于点O.
图1 图2 图3 图4
(一)探索发现
(1)如图1,当AB=2时,连接AD,则∠ADO=90°,BO=2DO,AD,BO ,tan∠AOD= .
如图2,当AB=3时,画AH⊥BD交BD的延长线于H,则AH ,
BO= ,tan∠AOD= .
如图3,当AB=4时,tan∠AOD= .
(2)猜想:当AB=n (n>0)时,tan∠AOD= .(结果用含n的代数式表示),请证明你的猜想.
(二)解决问题
(3)如图,两个正方形的一边CD、CG在同一直线上,连接CF、DE相交于点O,若tan∠COE,求正方形ABCD和正方形CEFG的边长之比.
解∶(一)探索发现
(1)如图1,当AB=2时,∵BO=2DO,BO,∴OD,又∵∠ADO=90°,AD,∴tan∠AOD3,即tan∠AOD=3.
如图2,设DCBE为正方形,连接CE,交BD于F.∵四边形BCDE是正方形,
∴DF=CF=BFBDCE,BD⊥CE.根据题意得∶AB∥DC,∴△AOB∽△COD,
∴DO∶BO=CD∶AB.当AB=3时,DO∶BO=1∶3,∴BO.∵S△ABDBD?AHAB?ED,∴BD?AH=AB?ED,∴AH,DO∶BO=CD∶AB=1∶3,∴DO∶DF=1∶2,∴OF∶DF=1∶2,即OF∶CF=1∶2.在Rt△OCF中,tan∠COF2,∵∠AOD=∠COF,∴tan∠AOD=2;如图3,当AB=4时,DO∶BO=CD∶AB=1∶4,∴DO∶DF=1∶2.5=2∶5,∴OF∶DF=3∶5,即OF∶CF=3∶5.在Rt△OCF中,tan∠COF,∵∠AOD=∠COF,∴tan∠AOD;故答案是3;;2;;
(2)猜想∶当AB=n(n>0)时,tan∠AOD(结果用含n的代数式表示).
证明∶过点A作AH⊥BH于点H,则AH=BHn.∵AB∥OD,∴△AOB∽△COD,
∴,∴OB.∴OH=BH﹣OBn.∴tan∠AOD;故答案是;
(二)解决问题
(3)解:如图4,过点D作DH⊥CF于点H,则tan∠DOH.∵∠DOH=∠COE,
∴tan∠DOH,又由(一)结论得:,
∴n,∴正方形ABCD和正方形CEFG的边长之比为 .
图1 图2 图3 图4
网格内的图形特点:为格点图形,则边长均可求;若不是格点图形,多边形内角可转换.
例题讲解
一、构造直角
例题1、网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则sinA= .
【解析】如图,作AD⊥BC于D,CE⊥AB于E,由勾股定理得AB=AC=2,BC=2,AD=3,可以得知△ABC是等腰三角形,由面积相等可得,BC?ADAB?CE,
即CE,sinA,故答案为.
【总结】由于格点三角形各边都可求,所以利用解直角三角形即可求出各个内角的三角函数值.
二、角度转换
例题2、如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是 .
思路一:构造直角
连接BE,由四边形EDBC为正方形可知,CD⊥BE,∴tan∠APD=tan∠BPF=,设小正方形边长为(思考一下为什么可以这么设?),可得BF=1,CD=2,由△ACP∽△BDP,且相似比为3∶1可得=3,∴=,∴PC=,∴PF=PC—CF=, ∴tan∠BPF.
思路二∶角度转换
连接BE,可知BE∥CD,∴∠APD=∠BPF=∠ABE,连接AE,AE和BE均为正方形对角线,易得AE⊥BE,tan∠ABE=.
例题3、在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A、B、C、D都在格点处,AB与CD相交于O,则tan∠BOD的值等于
【答案】3
【解析】
转化思路一:到格点三角形内,再用例题1的方法(此方法构造情况较多,解法较暴力,在此不一一列举,以下给出三种转化法)
转化思路二:思路一的情况下,存在转化出的格点三角形恰好为直角三角形,这类方法最巧妙,但需要学生有较强的观察能力!
直角构造思路三:通过连接某些辅助线,构造出直角后直接在直角三角形内求解.
巩固练习
1、如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是 .
【解析】连接AC,由网格特点和正方形的性质可知,∠BAC=90°,根据勾股定理得,AC,AB=2,则tan∠ABC,故答案为.
2、如图,在4x5的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则tan∠ABC= ;sin∠ACB= .
【解析】找到与A构成小正方形对角线的格点D、E,连接CD,AE,EB,AC与EB交于点F.由网格特点和正方形的性质可知,∠BAE=90°,根据勾股定理得,AE,AB=3,DB=2,DC=3,BE=,则tan∠ABC,又BE⊥AC,易得△AEF∽△BAF,故,∴,∴BF=,sin∠ACB=,故答案为3,.
3、如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则的值= ,tan∠APD的值= .
【解析】∵四边形BCED是正方形,∴DB∥AC,∴△DBP∽△CAP,∴3,
连接BE,∵四边形BCED是正方形,∴DF=CFCD,BFBE,CD=BE,BE⊥CD,∴BF=CF,根据题意得:AC∥BD,∴△ACP∽△BDP,∴DP:CP=BD:AC=1:3,
∴DP:DF=1:2,∴DP=PFCFBF,在Rt△PBF中,tan∠BPF2,
∵∠APD=∠BPF,∴tan∠APD=2,故答案为3,2.
4、如图,在正方形网格中,△ABC的顶点都在格点上,则tan∠ACB的值为 .
【解析】解:作AD⊥BC于D,由勾股定理得,AC,AB=3,BC=4,
△ABC的面积为:AB×CE=6,∴CB×AD=6,解得AD,
CD,tan∠ACB.故答案为.
5、如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是 .
【解析】如图,连接EA,EC,设菱形的边长为a,由题意得∠AEF=30°,∠BEF=60°,AEa,EB=2a,∴∠AEC=90°,∵∠ACE=∠ACG=∠BCG=60°,
∴E、C、B共线,在Rt△AEB中,tan∠ABC.故答案为.
第5题
6、如图,网格中的四个格点组成菱形ABCD,则tan∠DBC的值为 .
【解析】如图,连接AC与BD相交于点O,∵四边形ABCD是菱形,∴AC⊥BD,BOBD,COAC,由勾股定理得,AC3,BD,所以,BO,CO3,所以,tan∠DBC3.故答案为3.
7、如图1是由边长为1的小正方形组成的网格,点A、B、C、D都在网格的格点上,AC、BD相交于点O.
图1 图2 图3 图4
(一)探索发现
(1)如图1,当AB=2时,连接AD,则∠ADO=90°,BO=2DO,AD,BO ,tan∠AOD= .
如图2,当AB=3时,画AH⊥BD交BD的延长线于H,则AH ,
BO= ,tan∠AOD= .
如图3,当AB=4时,tan∠AOD= .
(2)猜想:当AB=n (n>0)时,tan∠AOD= .(结果用含n的代数式表示),请证明你的猜想.
(二)解决问题
(3)如图,两个正方形的一边CD、CG在同一直线上,连接CF、DE相交于点O,若tan∠COE,求正方形ABCD和正方形CEFG的边长之比.
解∶(一)探索发现
(1)如图1,当AB=2时,∵BO=2DO,BO,∴OD,又∵∠ADO=90°,AD,∴tan∠AOD3,即tan∠AOD=3.
如图2,设DCBE为正方形,连接CE,交BD于F.∵四边形BCDE是正方形,
∴DF=CF=BFBDCE,BD⊥CE.根据题意得∶AB∥DC,∴△AOB∽△COD,
∴DO∶BO=CD∶AB.当AB=3时,DO∶BO=1∶3,∴BO.∵S△ABDBD?AHAB?ED,∴BD?AH=AB?ED,∴AH,DO∶BO=CD∶AB=1∶3,∴DO∶DF=1∶2,∴OF∶DF=1∶2,即OF∶CF=1∶2.在Rt△OCF中,tan∠COF2,∵∠AOD=∠COF,∴tan∠AOD=2;如图3,当AB=4时,DO∶BO=CD∶AB=1∶4,∴DO∶DF=1∶2.5=2∶5,∴OF∶DF=3∶5,即OF∶CF=3∶5.在Rt△OCF中,tan∠COF,∵∠AOD=∠COF,∴tan∠AOD;故答案是3;;2;;
(2)猜想∶当AB=n(n>0)时,tan∠AOD(结果用含n的代数式表示).
证明∶过点A作AH⊥BH于点H,则AH=BHn.∵AB∥OD,∴△AOB∽△COD,
∴,∴OB.∴OH=BH﹣OBn.∴tan∠AOD;故答案是;
(二)解决问题
(3)解:如图4,过点D作DH⊥CF于点H,则tan∠DOH.∵∠DOH=∠COE,
∴tan∠DOH,又由(一)结论得:,
∴n,∴正方形ABCD和正方形CEFG的边长之比为 .
图1 图2 图3 图4
同课章节目录
