中考培优第二轮复习专题 第5章 尺规作图学案(含答案)
文档属性
| 名称 | 中考培优第二轮复习专题 第5章 尺规作图学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 12:12:36 | ||
图片预览

文档简介
第五章 尺规作图
基本知识
1.定义
只用没有刻度的________和________作图叫做尺规作图.
2.步骤
①根据给出的条件和求作的图形,写出已知和求作部分;
②分析作图的方法和过程;
③用直尺和圆规进行作图;
④写出作法步骤,即作法.
3.基本掌握要求
①能用尺规完成以下基本作图:作一条线段等于已知线段;作一个角等于已知角;作一个角的平分线;作一条线段的垂直平分线;过一点作已知直线的垂线.
②能利用基本作图作三角形:已知三边作三角形;己知两边及其夹角作三角形;已知两角及一边作三角形;已知底边和底边上的高作等腰三角形;已知一直角边和斜边作直角三角形.
③能利用基本作图完成:过不在同一直线上的三点作圆;会作三角形的外接圆(外心)、内切圆(内心);会作圆的内接正方形和正六边形.
④在尺规作图中,了解尺规作图的依据,保留作图痕迹,不要求写作法.
例题讲解
一、只用尺子
说明:一般指的是无刻度的直尺,无刻度直尺一般只能用来连接(部分题目也会给出直尺、有刻度尺子)
例题1 如图,在正方形ABCD中,点M是BC边上任意一点,请你仅用无刻度直尺,分别在图1、图2中按要求作图(保留作图痕迹,不写作法).
(1)在图(1)中,在AB边上求作一点N,连接CN,使CN=AM;
(2)在图(2)中,在AD边上求作一点Q,连接CQ,使CQ∥AM.
【解析】
(1)如图1,连接BD交AM于点E,连接CE延长交AB于点N,CN=AM;
(2)如图2,连接对角线BD与AC相交于点O,连接MO延长交AD于点Q,连接CQ,CO∥AM.
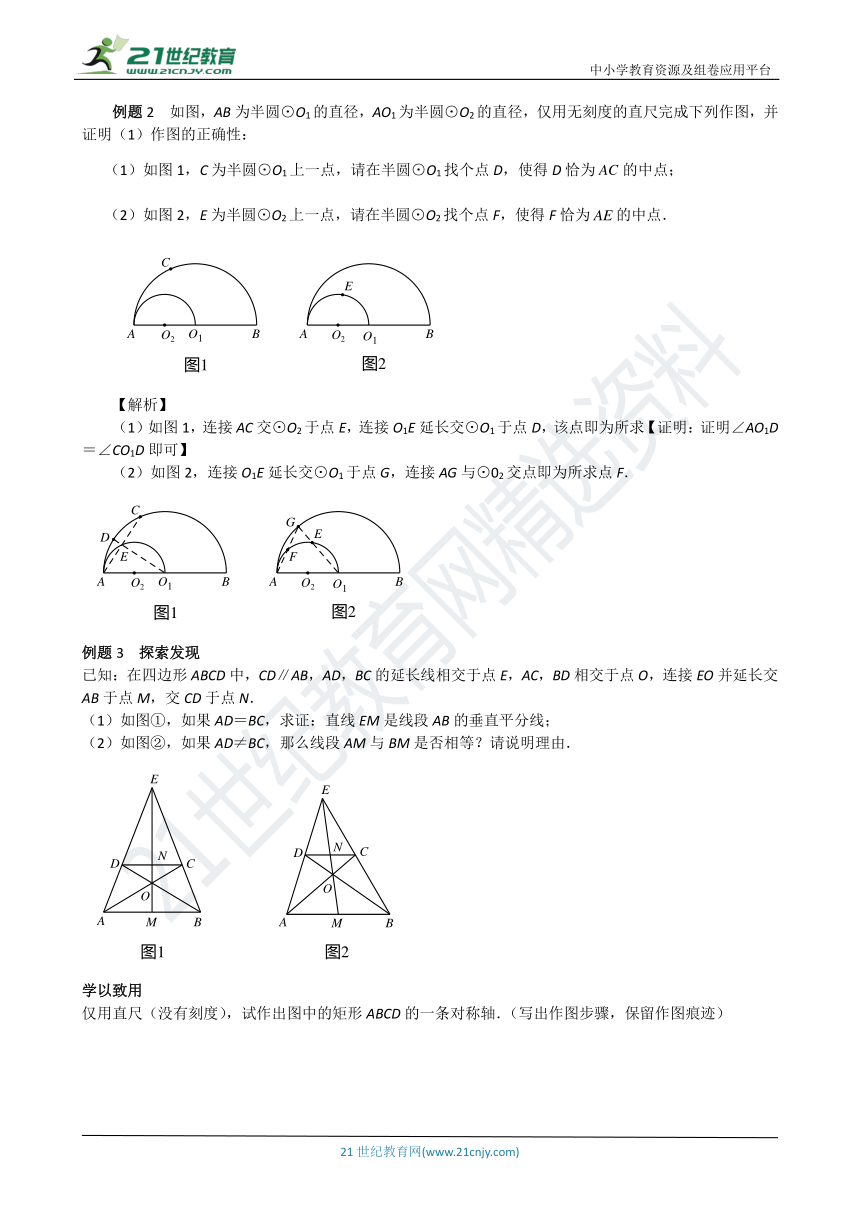
例题2 如图,AB为半圆⊙O1的直径,AO1为半圆⊙O2的直径,仅用无刻度的直尺完成下列作图,并证明(1)作图的正确性:
(1)如图1,C为半圆⊙O1上一点,请在半圆⊙O1找个点D,使得D恰为的中点;
(2)如图2,E为半圆⊙O2上一点,请在半圆⊙O2找个点F,使得F恰为的中点.
【解析】
(1)如图1,连接AC交⊙O2于点E,连接O1E延长交⊙O1于点D,该点即为所求【证明:证明∠AO1D=∠CO1D即可】
(2)如图2,连接O1E延长交⊙O1于点G,连接AG与⊙02交点即为所求点F.
例题3 探索发现
已知:在四边形ABCD中,CD∥AB,AD,BC的延长线相交于点E,AC,BD相交于点O,连接EO并延长交AB于点M,交CD于点N.
(1)如图①,如果AD=BC,求证:直线EM是线段AB的垂直平分线;
(2)如图②,如果AD≠BC,那么线段AM与BM是否相等?请说明理由.
学以致用
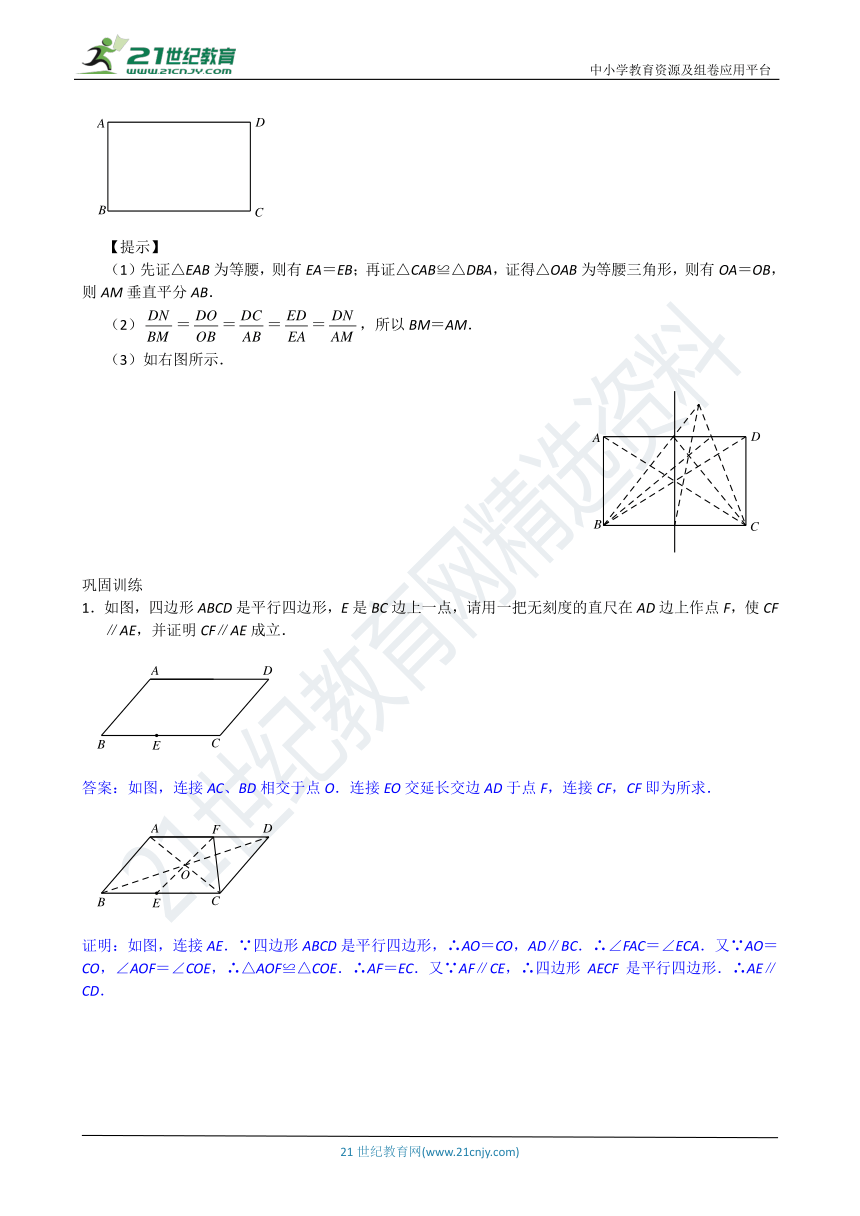
仅用直尺(没有刻度),试作出图中的矩形ABCD的一条对称轴.(写出作图步骤,保留作图痕迹)
【提示】
(1)先证△EAB为等腰,则有EA=EB;再证△CAB≌△DBA,证得△OAB为等腰三角形,则有OA=OB,则AM垂直平分AB.
(2)====,所以BM=AM.
(3)如右图所示.
巩固训练
1.如图,四边形ABCD是平行四边形,E是BC边上一点,请用一把无刻度的直尺在AD边上作点F,使CF∥AE,并证明CF∥AE成立.
答案:如图,连接AC、BD相交于点O.连接EO交延长交边AD于点F,连接CF,CF即为所求.
证明:如图,连接AE.∵四边形ABCD是平行四边形,∴AO=CO,AD∥BC.∴∠FAC=∠ECA.又∵AO=CO,∠AOF=∠COE,∴△AOF≌△COE.∴AF=EC.又∵AF∥CE,∴四边形AECF是平行四边形.∴AE∥CD.
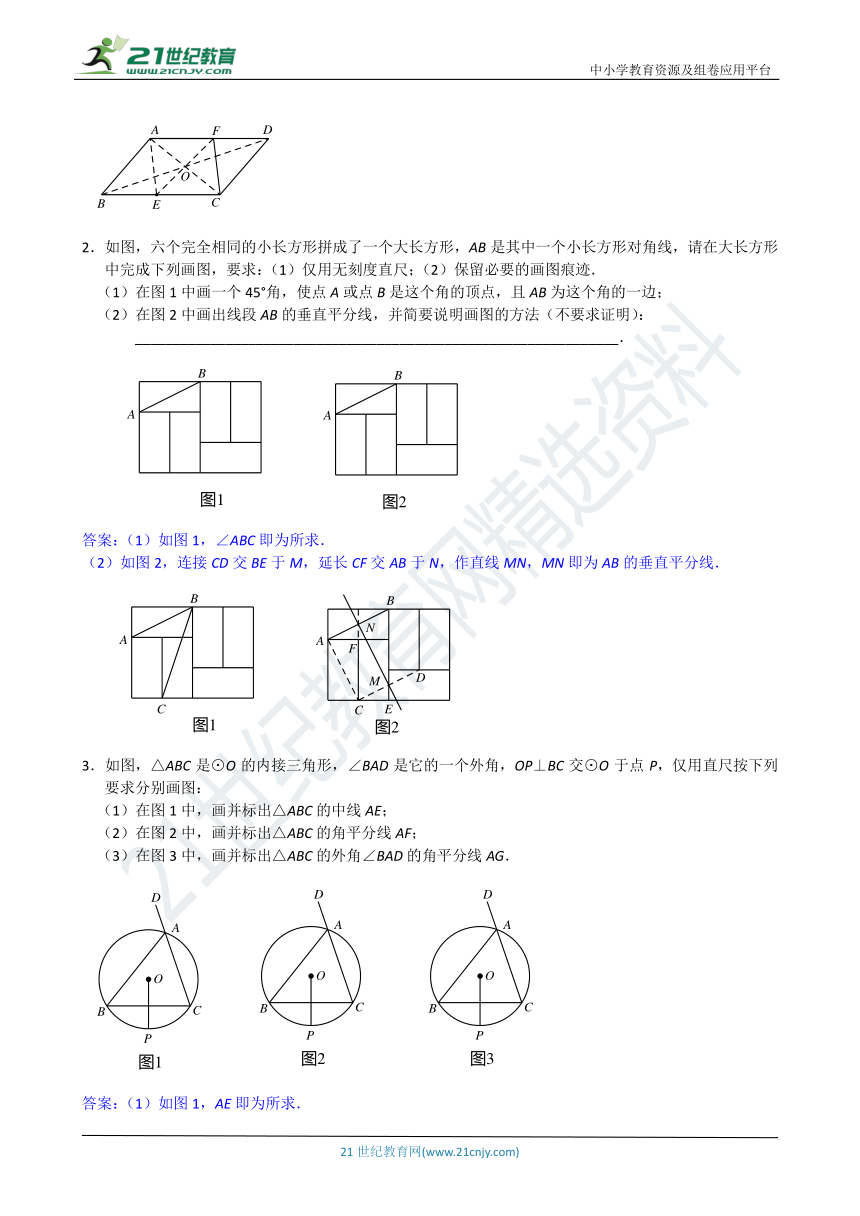
2.如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形对角线,请在大长方形中完成下列画图,要求:(1)仅用无刻度直尺;(2)保留必要的画图痕迹.
(1)在图1中画一个45°角,使点A或点B是这个角的顶点,且AB为这个角的一边;
(2)在图2中画出线段AB的垂直平分线,并简要说明画图的方法(不要求证明):
________________________________________________________________.
答案:(1)如图1,∠ABC即为所求.
(2)如图2,连接CD交BE于M,延长CF交AB于N,作直线MN,MN即为AB的垂直平分线.
3.如图,△ABC是⊙O的内接三角形,∠BAD是它的一个外角,OP⊥BC交⊙O于点P,仅用直尺按下列要求分别画图:
(1)在图1中,画并标出△ABC的中线AE;
(2)在图2中,画并标出△ABC的角平分线AF;
(3)在图3中,画并标出△ABC的外角∠BAD的角平分线AG.
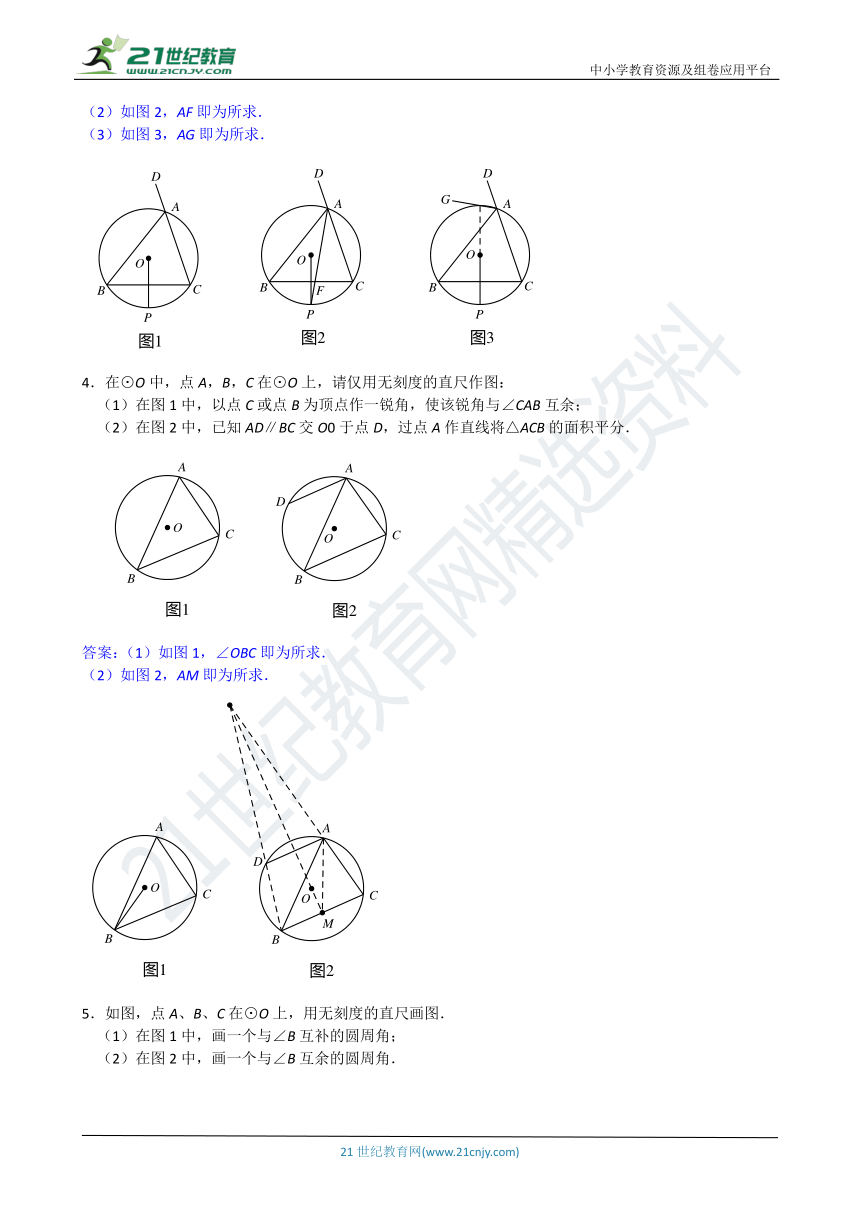
答案:(1)如图1,AE即为所求.
(2)如图2,AF即为所求.
(3)如图3,AG即为所求.
4.在⊙O中,点A,B,C在⊙O上,请仅用无刻度的直尺作图:
(1)在图1中,以点C或点B为顶点作一锐角,使该锐角与∠CAB互余;
(2)在图2中,已知AD∥BC交O0于点D,过点A作直线将△ACB的面积平分.
答案:(1)如图1,∠OBC即为所求.
(2)如图2,AM即为所求.
5.如图,点A、B、C在⊙O上,用无刻度的直尺画图.
(1)在图1中,画一个与∠B互补的圆周角;
(2)在图2中,画一个与∠B互余的圆周角.
答案:(1)如图1,∠D即为所求.
(2)如图2,∠DAC即为所求.
6.如图,AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.
(1)在图1中,画出△ABC中AB边上的高;
(2)在图2中,画出△ABC中AB边上的高.
答案:(1)如图1,CD即为所求
(2)如图2,CD即为所求.
7.如图,A、B、C、D为圆上四点,AB∥CD,AB<CD,请只用无刻度的直尺,画出圆的一条直径EF(不写画法,保留画图痕迹).
答案:如图,EF即为所求.
8.如图,△ABC中,D是BC的中点,点P在AB上.
(1)在图中只用直尺作过点P的直线l∥BC;
(2)求证:l∥BC.
答案:如图,直线l即为所求.
证明:如图,过点Q作MN∥BC,交AB、AC分别于点M、N.∵MN∥BC,∴△AMQ∽△ABD,△AQN∽△ADC.∴=,=.∴=.∵点D是BC的中点,∴BD=CD.∴MQ=NQ.∵MN∥BC,∴△PMQ∽△PBC,△EQN∽△EBC.∴=,=.∴=.∴=.又∵∠PQE=∠CQB,∴△PQE∽△CQB.∴∠EPQ=∠BCQ.∴PE∥BC,即l∥BC.
例题讲解
二、只用圆规
说明:只用圆规,只能确定“点”,无法出现“线”.
例题1 如图,所给两圆的圆心分别为O1,O2,半径都为3,根据要求完成作图(保留作图痕迹,不写作法).
(1)在图1中,仅用无刻度直尺作出圆上的两点A,B,使得=3π;
(2)在图2中,仅用圆规作出圆上的两点A,B,使得=2π.
【解析】
(1)画一条直径即可(直径AB);
(2)以圆上任意一点为圆心,OO2的半径为半径画圆,与OO2的两个交点即为A、B.
例题2 如图,△ABC中(∠BAC<60°),AB=AC,AD⊥BC于点D.
(1)如图1,试在AD上仅用圆规确定E点,使∠BEC=60°;(保留痕迹,不写画法)
(2)如图2,试在AD上仅用圆规确定F点,使∠BFC=45°;(保留痕迹,不写画法)
【解析】
(1)以B为圆心,BC长为半径画圆,与AD交点即为所求点E;
(2)以D为圆心,BD长为半径画圆,交AD于点G,再以点G为圆心,GB为半径画圆,与AD交点即为所求点F.
例题讲解
三、尺规作图
【基本作图】
作线段a
作∠α
作∠AOB的角平分线
作线段AB的垂直平分线
过点P作直线l的垂线
作点P关于直线l的对称点P′
作点P关于直线l的平行线
已知三条线段作△ABC
作△ABC,使得AB=a,AC=b,∠A=α
作△ABC,使得∠A=α,∠B=β,AB=a
作等腰△ABC,使得AB=AC=a,BC上的高为b
作△ABC的外接圆
作△ABC的内切圆
作AB和AC边上的高
作圆的一条直径
作OO的内接正三角形
作OO的内接正六边形
例题1 如图,一条公路的转弯处是一段圆弧.
(1)作出AB所在圆的圆心O;(用直尺和圆规作图,保留作图痕迹,不写作法)
(2)若AB的中点C到弦AB的距离为20 m,AB=80 m,求所在圆的半径.
【答案】
(1)在圆弧上任取一点C,作线段AC、BC的垂直平分线交点即为圆心O;
(2)50 m.
例题2 如图,线段AB绕点O顺时针旋转一定的角度得到线段A1B1.
(1)请用直尺和圆规作出旋转中心O;(不写作法,保留作图痕迹)
(2)连接OA、OA1、OB、OB1,如果∠AOA1=∠BOB1=α;OA=OA1=a;OB=OB1=b.则线段AB扫过的面积是________.
【答案】
(1)BB1与AA1的垂直平分线的交点即为旋转中心O;
(2))【大扇形减小扇形】
例题3 已知△ABC,∠A>∠C>∠B.
(1)如图1,在线段BC上找一点P,使得PA+PC=BC;(用直尺和圆规作图,保留作图痕迹,不写作法)
(2)如图2,在AB边上作一点Q,使得△AQC∽△ACB;(用直尺和圆规作图,保留作图痕迹,不写作法)
(3)求作一个△DEF,使得△DEF∽△ABC,且EF=BC.(用直尺和圆规作图,保留作图痕迹,不写作法)
【提示】
(1)作AB的垂直平分线与BC交点即为点P;
(2)在∠C处以AC为一边在三角形内部作∠ACQ=∠ABC即可;
(3)作出AB、AC的中点M、N,连接MN,再作一个△DEF≌△AMN.
答案:(1)如图所示
(2)如图所示:
(3)如图所示:
例题4、我们知道,等边三角形三边相等,若将一个等边△ABC如图1所示展开,我们可以发现A、B为线段C'C"的两个三等分点。
(1)试根据上述方法,利用尺规在图2中作出线段AB的三等分点;
(2)请用不同于(1)的方法在图3中做出线段AB的一个三等分点,并说明理由。
图1 图2 图3
【解析】
(1)作AB的垂直平分线,再作出等边△ABC,接着作BC的垂直平分线交AB垂直平分线于点D,连接AD、BD,最后分别作AD、BD的垂直平分线,与AB交点分别为E,F,E、F即为AB三等分点,
(2)答案不唯一,这边给出一种。分别过A、B作AB的垂线,然后在两条垂线上截钱段,使得BE=2AC,连接CE交AB于点G,点G即为一个三等分点。
答案:如图所示
例题5、“位似变化”是一种重要的几何变化。可以将图形放大或缩小,且与原图形相似.你能用位似变化解决下列问题吗?
如图Rt△ABC中,∠C=90°,AC=12,BC=6,有矩形EFGH的一边EF在边AC上,点H在斜边AC上,EF=2,HE=1.
(1)请你用圆规和无刻度直尺在Rt△ABC内作一个最大的矩彩且与矩形EFGH位似。(不要求写作法,但必须保留作图痕迹)
(2)请证明你作图方法的正确性。
【解析】
(1)连接AG延长交BC于点P,过点P作BC垂线交AB于点M,最后再过点M作AC垂线,垂足为N,则矩形CPMN即为所求;
(2)根据(1)中的要求,一个是最大,一个是相似
① ,再加上∠HGF=∠MPC=90°,即可证得相似,所以
设CP=x,则MP=2x,BP=x,所以2x=6,解得x=3,即PC=3;
②设PC=m,则P8=6-m, ,所以,易知当m=3时,矩形面积最大,所以当PC=3时符合①要求。
例题6、【回归课本】
我们曾学习过一个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
【初步体验】
(1)如图1,在△ABC中,点D、F在AB上,E、G在AC上,DE∥FC∥BC.若AD=2,AE=1,DF=6,则EG= , .
(2)如图2,在△ABC中,点D、F在AB上,E、G在AC上,且DE∥BC∥FG.以AD、DF、FB为边构造△ADM(即AM=BF,MD=DF);以AE、EG、GC为边构造△AEN(即AN=GC,NE=EG).求证:∠M=∠N.
【深入探究】
(3)如图,已知△ABC和线段a,请用直尺与圆规作△A'B'C'.
满足:①△A'BC'∽△ABC;②△A'B'C'的周长等于线段a的长度.(保留作图痕迹,并写出作图步骤)
【解析】
(1)3;2;
(2)∵DE∥NG∥BC,∴,,∴,∵DF=DM,EG=EN,BF=AM,GC=AN,∴
∴△AMD∽△ANE,∴∠M=∠N
(3)过点A作任意射线AM,在射线AM上截取AB、BC、CD(CD=AC)的长度,连接DD'(AD'=a),过点C、B分别作DD'的平行线,分别交AD'于点C'、B',最后以AB'、B'C'、C'D'三边长度构建三角形即可
巩固练习
1、如图,在平行四边形ABCD中,已知AD>AB.
(1)实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形ABEF的形状,并给予证明.
答案:(1)如图所示
(2)四边形ABEF是菱形,理由如下:
∵四边形ABCD是平行四边形
∴AD∥BC
∴∠DAE=∠AEB,
又∵AE平分∠BAD
∴∠BAE=∠DAE
∴∠BAE=∠AEB
∴BE=AB,
由(1)得:AF=AB,
∴BE=AF,
又∵BE∥AF,
∴四边形ABEF是平行四边形,
∵AF=AB,
∴四边形ABEF是菱形。
2、如图,在矩形ABCD中,AB=4,BC=6,若点P在AD边上,连接BP、PC,使得△BPC是一个等腰三角形.
(1)用尺规作图画出符合要求的点P.(保留作图痕迹,不要求写做法)
(2)求出PA的长.
答案:
(1)如图所示:P,P1,P2即为所示;
(2)当BC=BP1=6时,∵AB=4,∴;
当CB=CP2=6时,P2A=AD-P2D=
当PB=PC时,PA=AD=3.
综合得,PA的长为,,3.
3、点P在△ABC内,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形与△ABC相似,那么就称点P为△ABC的自相似点.如图,在△ABC中,∠A<∠B<∠C.如图,利用尺规作出△ABC的所有自相似点P(写出作法并保留作图痕迹);
图1 备用图
答案:
作法:①在∠ABC内作∠CBD=∠A;
②在∠ACB内作∠BCE=∠ABC,BD交CE于点P,则点P为△ABC的自相似点。
4、已知在Rt△ABC中,∠C=90°,AC=4,BC=3,请用直尺(无刻度)和圆规按照要求作图.
(1)在图1中作一个平行四边形,使它的三个顶点恰好是△ABC的三个顶点(只需作一个,不写作法,保留作图痕迹).
(2)如图2,在边AB上作一点P,使得点P到边AC、BC的距离相等,此时PB= .(不写作法,保留作图痕迹);
(3)如图3,在AC边上找一点E,使得CE+BE=4,此时BE= .(不写作法,保留作图痕迹);
(4)如图4,在边AB上作一点G,使得点G到边AC的距离与GB相等(不写作法,保留作图痕迹).
图1 图2
图3 图4
答案:(1)如图所示:
(2)PB=,图形如下:
(3),图形如下:
(4)图形如下:
5.已知一个三角形的两条边长分别是1cm和2cm,一个内角为40°.
(1)请你借助图1画出一个满足题设条件的三角形;
(2)你是否还能画出既满足题设条件,又与(1)中所画的三角形不全等的三角形?若能,请你在备用图中,用“尺规作图”作出所有这样的三角形;若不能,请说明理由.
(3)如果将题设条件改为“三角形的两条边长分别是3cm和4cm,一个内角为40°”,那么满足这一条件,且彼此不全等的三角形有 个.
答案:(1)如图所示:
(2)如图所示:
(3)如图所示:满足这一条件,且彼此不全等的三角形有4个.
6.已知,如图,线段AB,利用无刻度的直尺和圆规,作一个满足条件的△ABC:①△ABC为直角三角形;②tan∠A=.(注:不要求写作法,但保留作图痕迹)
答案:如图所示:△ABC为所求作图形.
7.如图,OA=2,以点A为圆心,1为半径画⊙A与OA的延长线交于点C,过点A画OA的垂线,垂线与⊙A的一个交点为B,连接BC.
(1)线段BC的长等于 ;
(2)请在图中按下列要求逐一操作,并回答问题:
①以点 为圆心,以线段 的长为半径画弧,与射线BA交于点D,使线段OD的长等于.②连OD,在OD上画出点P,使OP得长等于,请写出画法,并说明理由.
答案:(1);(2)①A,BC;②如图所示:连接CD,过点A作AP∥CD交OD于点P.∵AP∥CD,∴==,∵BC===AD,∴OD==,∴OP=.
8.已知:线段a及∠ACB.求作:⊙O,使⊙O在∠ACB的内部,CO=a,且⊙O与∠ACB的两边分别相切.
答案:如图所示作∠BAC的角平分线,在角平分线上取点CO=a,以点O为圆心⊙O与AB、AC都相切.则⊙O即为所求作图形.
9.如图,已知∠BAC,在角的内部有一点P,请画一个⊙M,使得⊙M经过点P,且与AB、AC都相切.(注:并简要说明画法)【提示:用位似】
答案:如图所示:作∠BAC的角平分线,在角平分线上取点O作⊙O与AB、AC都相切,再连接AP,与⊙O与交于点N,过点P作PM∥ON交AO于点M,过点M作⊙M与AB、AC都相切.则⊙M即为所求作图形.
10.如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)作△ABC的外心O;
(2)设D是AB边上一点,在图中作出一个正六边形DEFGHI,使点F、点H分别在边BC和AC上.
答案:(1)如图所示:点O即为所求图形.
(2)则六边形DEFGHI即为所求作图形.
11.在△ABC中,D为BC边上一点.
(1)如图①,在Rt△ABC中,∠C=90°,将△ABC沿着AD折叠,点C落在AB边上.请用直尺和圆规作出点D(不写作法,保留作图痕迹);
(2)如图②,将△ABC沿着过点D的直线折叠,点C落在AB边上的E处.
①若DE⊥AB,垂足为E,请用直尺和圆规作出点D(不写作法,保留作图痕迹);
②若AB=4,BC=6,∠B=45°,则CD的取值范围是 .
答案:(1)如图所示:点D即为所求.
(2)①如图所示:点D即为所求.
②6-6≤CD≤5.
12.如图,a、b、c是三条互相平行的直线,点A在直线a上,请用尺规完成以下作图(不要求写作法,但要保留作图痕迹)
(1)作等腰直角△APQ,其中∠APQ=90°,P、Q都在直线c上(P在Q右侧);
(2)作等腰直角△AMN,其中∠AMN=90°,M、N分别在直线b、c上.
答案:(1)如图所示:△APQ即为所求.
(2)如图所示:△AMN即为所求.
13.(1)如图1,Rt△ABC中,∠B=90°,AB=2BC,现以C为圆心、CB长为半径画弧交边AC于D,再以A为圆心、AD为半径画弧交边AB于E.
求证:=.(这个比值叫做AE与AB的黄金比.)
(2)如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请你以图2中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.
(注:直尺没有刻度!作图不要求写作法,但要求保留作图痕迹,并对作图中涉及到的点用字母进行标注)
答案:(1)设BC=CD=x,则AB=2BC=2x.在Rt△ABC中,AB==x,∴AE=AD=AC-CD=(-1) x,∴=.
(2)如图所示:△ABF即为所求.
作AB的垂直平分线,交AB于D,过B作AB垂线,在垂线上截取BC=BD,连接AC,在AC上截取CE=BC,分别以A、B为圆心,AB、AE为半径画圆,交于点F.△ABF即为所求图形.
14、【缘起】苏教版九下P56,“如图1,在Rt△ABC中,∠ACB=90°,CD是△ABC的高,则△ACD与△CBD相似吗?”于是,学生甲发现CD2=AD·BD也成立.
问题1:请你证明CD2=AD·BD;
学生乙从CD2=AD·BD中得出:可以画出两条已知线段的比例中项.
证明:∵∠ACB=90°,CD是△ABC的高,∴∠ADC=∠CDB=90°,∵∠ACD+∠DCB=∠ACB=90°,∠ACD+∠A=90°,∴∠DCB=∠A,∴△ACD∽△CBD,∴=,∴CD2=AD·BD;
问题2:已知两条线段AB、BC在x轴上,如图2:请你用直尺(无刻度)和圆规作出这两条线段的比例中项.要求保留作图痕迹,不要写作法,最后指出所要作的线段.
答案:如图所示:线段DO即为所求.
学生丙也从CD2=AD·BD中悟出了矩形与正方形的等积作法.
问题3:如图3,已知矩形ABCD,请你用直尺(无刻度)和圆规作出一个正方形BMNP,使得S正方形BMNP=S矩形ABCD.要求:保留作图痕迹;简要写出作图每个步骤的要点.
答案:如图所示:四边形BMNP即为所求.
15.【回归课本】我们曾学习过这样的基本事实:①线段垂直平分线上的点到线段两端的距离相等;②同弧所对的圆周角相等.
【初步体验】如图,已知△ABC,用没有刻度的直尺和圆规作图,不要求写作法,但要保留作图痕迹,并对作图中涉及到的点用字母进行标注.
(1)在图1中AC边上找点D,使DB+DC=AC;
(2)在图2中作△BCE,使∠BEC=∠BAC,CE=BE.
答案:(1)如图所示:点D即为所求.
(2)如图所示:△BCE即为所求.
【深入探究】小明运用上述基本事实解决了下面一个问题:
(3)如图3,已知线段a和等边△ABC,作△BCM,使∠BMC=∠BAC,BM+CM=a.
他的做法是:
1画△ABC的外接圆;
2以A为圆心、AB长为半径画⊙A;
3以C为圆心、a为半径画弧与⊙A交于点F;
4连接CF与△ABC的外接圆交于点M,则△BCM是要画的三角形.
请你给出证明,并直接写出这样的点M有 个.
证明:连接BF.∵△ABC是等边三角形,∴∠BAC=60°,∴∠BMC=∠BAC=60°,∠BFC=∠BAC=30°,∴∠MBF=∠BMC-∠BFC=30°,∴∠MBF=∠BFC,∴MF=BM,∵MF+MC=FC=a,∴BM+MC=a.
如图所示:点M、M1、M2、M3为所求点,共4个.
(3)请你仿照小明的做法解决下面的问题:
如图4,已知线段b和△ABC,作△BCN,使∠BNC=∠BAC,BN-CN=b.
答案:作△ABC的外接圆,分别作∠ACB、∠ABC的平分线,交于点G,作△BCG的外接圆,以点B为圆心,b为半径交△BCG的外接圆于F,延长BF交△ABC的外接圆于点N,连接CN.则BN-CN=b.
基本知识
1.定义
只用没有刻度的________和________作图叫做尺规作图.
2.步骤
①根据给出的条件和求作的图形,写出已知和求作部分;
②分析作图的方法和过程;
③用直尺和圆规进行作图;
④写出作法步骤,即作法.
3.基本掌握要求
①能用尺规完成以下基本作图:作一条线段等于已知线段;作一个角等于已知角;作一个角的平分线;作一条线段的垂直平分线;过一点作已知直线的垂线.
②能利用基本作图作三角形:已知三边作三角形;己知两边及其夹角作三角形;已知两角及一边作三角形;已知底边和底边上的高作等腰三角形;已知一直角边和斜边作直角三角形.
③能利用基本作图完成:过不在同一直线上的三点作圆;会作三角形的外接圆(外心)、内切圆(内心);会作圆的内接正方形和正六边形.
④在尺规作图中,了解尺规作图的依据,保留作图痕迹,不要求写作法.
例题讲解
一、只用尺子
说明:一般指的是无刻度的直尺,无刻度直尺一般只能用来连接(部分题目也会给出直尺、有刻度尺子)
例题1 如图,在正方形ABCD中,点M是BC边上任意一点,请你仅用无刻度直尺,分别在图1、图2中按要求作图(保留作图痕迹,不写作法).
(1)在图(1)中,在AB边上求作一点N,连接CN,使CN=AM;
(2)在图(2)中,在AD边上求作一点Q,连接CQ,使CQ∥AM.
【解析】
(1)如图1,连接BD交AM于点E,连接CE延长交AB于点N,CN=AM;
(2)如图2,连接对角线BD与AC相交于点O,连接MO延长交AD于点Q,连接CQ,CO∥AM.
例题2 如图,AB为半圆⊙O1的直径,AO1为半圆⊙O2的直径,仅用无刻度的直尺完成下列作图,并证明(1)作图的正确性:
(1)如图1,C为半圆⊙O1上一点,请在半圆⊙O1找个点D,使得D恰为的中点;
(2)如图2,E为半圆⊙O2上一点,请在半圆⊙O2找个点F,使得F恰为的中点.
【解析】
(1)如图1,连接AC交⊙O2于点E,连接O1E延长交⊙O1于点D,该点即为所求【证明:证明∠AO1D=∠CO1D即可】
(2)如图2,连接O1E延长交⊙O1于点G,连接AG与⊙02交点即为所求点F.
例题3 探索发现
已知:在四边形ABCD中,CD∥AB,AD,BC的延长线相交于点E,AC,BD相交于点O,连接EO并延长交AB于点M,交CD于点N.
(1)如图①,如果AD=BC,求证:直线EM是线段AB的垂直平分线;
(2)如图②,如果AD≠BC,那么线段AM与BM是否相等?请说明理由.
学以致用
仅用直尺(没有刻度),试作出图中的矩形ABCD的一条对称轴.(写出作图步骤,保留作图痕迹)
【提示】
(1)先证△EAB为等腰,则有EA=EB;再证△CAB≌△DBA,证得△OAB为等腰三角形,则有OA=OB,则AM垂直平分AB.
(2)====,所以BM=AM.
(3)如右图所示.
巩固训练
1.如图,四边形ABCD是平行四边形,E是BC边上一点,请用一把无刻度的直尺在AD边上作点F,使CF∥AE,并证明CF∥AE成立.
答案:如图,连接AC、BD相交于点O.连接EO交延长交边AD于点F,连接CF,CF即为所求.
证明:如图,连接AE.∵四边形ABCD是平行四边形,∴AO=CO,AD∥BC.∴∠FAC=∠ECA.又∵AO=CO,∠AOF=∠COE,∴△AOF≌△COE.∴AF=EC.又∵AF∥CE,∴四边形AECF是平行四边形.∴AE∥CD.
2.如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形对角线,请在大长方形中完成下列画图,要求:(1)仅用无刻度直尺;(2)保留必要的画图痕迹.
(1)在图1中画一个45°角,使点A或点B是这个角的顶点,且AB为这个角的一边;
(2)在图2中画出线段AB的垂直平分线,并简要说明画图的方法(不要求证明):
________________________________________________________________.
答案:(1)如图1,∠ABC即为所求.
(2)如图2,连接CD交BE于M,延长CF交AB于N,作直线MN,MN即为AB的垂直平分线.
3.如图,△ABC是⊙O的内接三角形,∠BAD是它的一个外角,OP⊥BC交⊙O于点P,仅用直尺按下列要求分别画图:
(1)在图1中,画并标出△ABC的中线AE;
(2)在图2中,画并标出△ABC的角平分线AF;
(3)在图3中,画并标出△ABC的外角∠BAD的角平分线AG.
答案:(1)如图1,AE即为所求.
(2)如图2,AF即为所求.
(3)如图3,AG即为所求.
4.在⊙O中,点A,B,C在⊙O上,请仅用无刻度的直尺作图:
(1)在图1中,以点C或点B为顶点作一锐角,使该锐角与∠CAB互余;
(2)在图2中,已知AD∥BC交O0于点D,过点A作直线将△ACB的面积平分.
答案:(1)如图1,∠OBC即为所求.
(2)如图2,AM即为所求.
5.如图,点A、B、C在⊙O上,用无刻度的直尺画图.
(1)在图1中,画一个与∠B互补的圆周角;
(2)在图2中,画一个与∠B互余的圆周角.
答案:(1)如图1,∠D即为所求.
(2)如图2,∠DAC即为所求.
6.如图,AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.
(1)在图1中,画出△ABC中AB边上的高;
(2)在图2中,画出△ABC中AB边上的高.
答案:(1)如图1,CD即为所求
(2)如图2,CD即为所求.
7.如图,A、B、C、D为圆上四点,AB∥CD,AB<CD,请只用无刻度的直尺,画出圆的一条直径EF(不写画法,保留画图痕迹).
答案:如图,EF即为所求.
8.如图,△ABC中,D是BC的中点,点P在AB上.
(1)在图中只用直尺作过点P的直线l∥BC;
(2)求证:l∥BC.
答案:如图,直线l即为所求.
证明:如图,过点Q作MN∥BC,交AB、AC分别于点M、N.∵MN∥BC,∴△AMQ∽△ABD,△AQN∽△ADC.∴=,=.∴=.∵点D是BC的中点,∴BD=CD.∴MQ=NQ.∵MN∥BC,∴△PMQ∽△PBC,△EQN∽△EBC.∴=,=.∴=.∴=.又∵∠PQE=∠CQB,∴△PQE∽△CQB.∴∠EPQ=∠BCQ.∴PE∥BC,即l∥BC.
例题讲解
二、只用圆规
说明:只用圆规,只能确定“点”,无法出现“线”.
例题1 如图,所给两圆的圆心分别为O1,O2,半径都为3,根据要求完成作图(保留作图痕迹,不写作法).
(1)在图1中,仅用无刻度直尺作出圆上的两点A,B,使得=3π;
(2)在图2中,仅用圆规作出圆上的两点A,B,使得=2π.
【解析】
(1)画一条直径即可(直径AB);
(2)以圆上任意一点为圆心,OO2的半径为半径画圆,与OO2的两个交点即为A、B.
例题2 如图,△ABC中(∠BAC<60°),AB=AC,AD⊥BC于点D.
(1)如图1,试在AD上仅用圆规确定E点,使∠BEC=60°;(保留痕迹,不写画法)
(2)如图2,试在AD上仅用圆规确定F点,使∠BFC=45°;(保留痕迹,不写画法)
【解析】
(1)以B为圆心,BC长为半径画圆,与AD交点即为所求点E;
(2)以D为圆心,BD长为半径画圆,交AD于点G,再以点G为圆心,GB为半径画圆,与AD交点即为所求点F.
例题讲解
三、尺规作图
【基本作图】
作线段a
作∠α
作∠AOB的角平分线
作线段AB的垂直平分线
过点P作直线l的垂线
作点P关于直线l的对称点P′
作点P关于直线l的平行线
已知三条线段作△ABC
作△ABC,使得AB=a,AC=b,∠A=α
作△ABC,使得∠A=α,∠B=β,AB=a
作等腰△ABC,使得AB=AC=a,BC上的高为b
作△ABC的外接圆
作△ABC的内切圆
作AB和AC边上的高
作圆的一条直径
作OO的内接正三角形
作OO的内接正六边形
例题1 如图,一条公路的转弯处是一段圆弧.
(1)作出AB所在圆的圆心O;(用直尺和圆规作图,保留作图痕迹,不写作法)
(2)若AB的中点C到弦AB的距离为20 m,AB=80 m,求所在圆的半径.
【答案】
(1)在圆弧上任取一点C,作线段AC、BC的垂直平分线交点即为圆心O;
(2)50 m.
例题2 如图,线段AB绕点O顺时针旋转一定的角度得到线段A1B1.
(1)请用直尺和圆规作出旋转中心O;(不写作法,保留作图痕迹)
(2)连接OA、OA1、OB、OB1,如果∠AOA1=∠BOB1=α;OA=OA1=a;OB=OB1=b.则线段AB扫过的面积是________.
【答案】
(1)BB1与AA1的垂直平分线的交点即为旋转中心O;
(2))【大扇形减小扇形】
例题3 已知△ABC,∠A>∠C>∠B.
(1)如图1,在线段BC上找一点P,使得PA+PC=BC;(用直尺和圆规作图,保留作图痕迹,不写作法)
(2)如图2,在AB边上作一点Q,使得△AQC∽△ACB;(用直尺和圆规作图,保留作图痕迹,不写作法)
(3)求作一个△DEF,使得△DEF∽△ABC,且EF=BC.(用直尺和圆规作图,保留作图痕迹,不写作法)
【提示】
(1)作AB的垂直平分线与BC交点即为点P;
(2)在∠C处以AC为一边在三角形内部作∠ACQ=∠ABC即可;
(3)作出AB、AC的中点M、N,连接MN,再作一个△DEF≌△AMN.
答案:(1)如图所示
(2)如图所示:
(3)如图所示:
例题4、我们知道,等边三角形三边相等,若将一个等边△ABC如图1所示展开,我们可以发现A、B为线段C'C"的两个三等分点。
(1)试根据上述方法,利用尺规在图2中作出线段AB的三等分点;
(2)请用不同于(1)的方法在图3中做出线段AB的一个三等分点,并说明理由。
图1 图2 图3
【解析】
(1)作AB的垂直平分线,再作出等边△ABC,接着作BC的垂直平分线交AB垂直平分线于点D,连接AD、BD,最后分别作AD、BD的垂直平分线,与AB交点分别为E,F,E、F即为AB三等分点,
(2)答案不唯一,这边给出一种。分别过A、B作AB的垂线,然后在两条垂线上截钱段,使得BE=2AC,连接CE交AB于点G,点G即为一个三等分点。
答案:如图所示
例题5、“位似变化”是一种重要的几何变化。可以将图形放大或缩小,且与原图形相似.你能用位似变化解决下列问题吗?
如图Rt△ABC中,∠C=90°,AC=12,BC=6,有矩形EFGH的一边EF在边AC上,点H在斜边AC上,EF=2,HE=1.
(1)请你用圆规和无刻度直尺在Rt△ABC内作一个最大的矩彩且与矩形EFGH位似。(不要求写作法,但必须保留作图痕迹)
(2)请证明你作图方法的正确性。
【解析】
(1)连接AG延长交BC于点P,过点P作BC垂线交AB于点M,最后再过点M作AC垂线,垂足为N,则矩形CPMN即为所求;
(2)根据(1)中的要求,一个是最大,一个是相似
① ,再加上∠HGF=∠MPC=90°,即可证得相似,所以
设CP=x,则MP=2x,BP=x,所以2x=6,解得x=3,即PC=3;
②设PC=m,则P8=6-m, ,所以,易知当m=3时,矩形面积最大,所以当PC=3时符合①要求。
例题6、【回归课本】
我们曾学习过一个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
【初步体验】
(1)如图1,在△ABC中,点D、F在AB上,E、G在AC上,DE∥FC∥BC.若AD=2,AE=1,DF=6,则EG= , .
(2)如图2,在△ABC中,点D、F在AB上,E、G在AC上,且DE∥BC∥FG.以AD、DF、FB为边构造△ADM(即AM=BF,MD=DF);以AE、EG、GC为边构造△AEN(即AN=GC,NE=EG).求证:∠M=∠N.
【深入探究】
(3)如图,已知△ABC和线段a,请用直尺与圆规作△A'B'C'.
满足:①△A'BC'∽△ABC;②△A'B'C'的周长等于线段a的长度.(保留作图痕迹,并写出作图步骤)
【解析】
(1)3;2;
(2)∵DE∥NG∥BC,∴,,∴,∵DF=DM,EG=EN,BF=AM,GC=AN,∴
∴△AMD∽△ANE,∴∠M=∠N
(3)过点A作任意射线AM,在射线AM上截取AB、BC、CD(CD=AC)的长度,连接DD'(AD'=a),过点C、B分别作DD'的平行线,分别交AD'于点C'、B',最后以AB'、B'C'、C'D'三边长度构建三角形即可
巩固练习
1、如图,在平行四边形ABCD中,已知AD>AB.
(1)实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形ABEF的形状,并给予证明.
答案:(1)如图所示
(2)四边形ABEF是菱形,理由如下:
∵四边形ABCD是平行四边形
∴AD∥BC
∴∠DAE=∠AEB,
又∵AE平分∠BAD
∴∠BAE=∠DAE
∴∠BAE=∠AEB
∴BE=AB,
由(1)得:AF=AB,
∴BE=AF,
又∵BE∥AF,
∴四边形ABEF是平行四边形,
∵AF=AB,
∴四边形ABEF是菱形。
2、如图,在矩形ABCD中,AB=4,BC=6,若点P在AD边上,连接BP、PC,使得△BPC是一个等腰三角形.
(1)用尺规作图画出符合要求的点P.(保留作图痕迹,不要求写做法)
(2)求出PA的长.
答案:
(1)如图所示:P,P1,P2即为所示;
(2)当BC=BP1=6时,∵AB=4,∴;
当CB=CP2=6时,P2A=AD-P2D=
当PB=PC时,PA=AD=3.
综合得,PA的长为,,3.
3、点P在△ABC内,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形与△ABC相似,那么就称点P为△ABC的自相似点.如图,在△ABC中,∠A<∠B<∠C.如图,利用尺规作出△ABC的所有自相似点P(写出作法并保留作图痕迹);
图1 备用图
答案:
作法:①在∠ABC内作∠CBD=∠A;
②在∠ACB内作∠BCE=∠ABC,BD交CE于点P,则点P为△ABC的自相似点。
4、已知在Rt△ABC中,∠C=90°,AC=4,BC=3,请用直尺(无刻度)和圆规按照要求作图.
(1)在图1中作一个平行四边形,使它的三个顶点恰好是△ABC的三个顶点(只需作一个,不写作法,保留作图痕迹).
(2)如图2,在边AB上作一点P,使得点P到边AC、BC的距离相等,此时PB= .(不写作法,保留作图痕迹);
(3)如图3,在AC边上找一点E,使得CE+BE=4,此时BE= .(不写作法,保留作图痕迹);
(4)如图4,在边AB上作一点G,使得点G到边AC的距离与GB相等(不写作法,保留作图痕迹).
图1 图2
图3 图4
答案:(1)如图所示:
(2)PB=,图形如下:
(3),图形如下:
(4)图形如下:
5.已知一个三角形的两条边长分别是1cm和2cm,一个内角为40°.
(1)请你借助图1画出一个满足题设条件的三角形;
(2)你是否还能画出既满足题设条件,又与(1)中所画的三角形不全等的三角形?若能,请你在备用图中,用“尺规作图”作出所有这样的三角形;若不能,请说明理由.
(3)如果将题设条件改为“三角形的两条边长分别是3cm和4cm,一个内角为40°”,那么满足这一条件,且彼此不全等的三角形有 个.
答案:(1)如图所示:
(2)如图所示:
(3)如图所示:满足这一条件,且彼此不全等的三角形有4个.
6.已知,如图,线段AB,利用无刻度的直尺和圆规,作一个满足条件的△ABC:①△ABC为直角三角形;②tan∠A=.(注:不要求写作法,但保留作图痕迹)
答案:如图所示:△ABC为所求作图形.
7.如图,OA=2,以点A为圆心,1为半径画⊙A与OA的延长线交于点C,过点A画OA的垂线,垂线与⊙A的一个交点为B,连接BC.
(1)线段BC的长等于 ;
(2)请在图中按下列要求逐一操作,并回答问题:
①以点 为圆心,以线段 的长为半径画弧,与射线BA交于点D,使线段OD的长等于.②连OD,在OD上画出点P,使OP得长等于,请写出画法,并说明理由.
答案:(1);(2)①A,BC;②如图所示:连接CD,过点A作AP∥CD交OD于点P.∵AP∥CD,∴==,∵BC===AD,∴OD==,∴OP=.
8.已知:线段a及∠ACB.求作:⊙O,使⊙O在∠ACB的内部,CO=a,且⊙O与∠ACB的两边分别相切.
答案:如图所示作∠BAC的角平分线,在角平分线上取点CO=a,以点O为圆心⊙O与AB、AC都相切.则⊙O即为所求作图形.
9.如图,已知∠BAC,在角的内部有一点P,请画一个⊙M,使得⊙M经过点P,且与AB、AC都相切.(注:并简要说明画法)【提示:用位似】
答案:如图所示:作∠BAC的角平分线,在角平分线上取点O作⊙O与AB、AC都相切,再连接AP,与⊙O与交于点N,过点P作PM∥ON交AO于点M,过点M作⊙M与AB、AC都相切.则⊙M即为所求作图形.
10.如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)作△ABC的外心O;
(2)设D是AB边上一点,在图中作出一个正六边形DEFGHI,使点F、点H分别在边BC和AC上.
答案:(1)如图所示:点O即为所求图形.
(2)则六边形DEFGHI即为所求作图形.
11.在△ABC中,D为BC边上一点.
(1)如图①,在Rt△ABC中,∠C=90°,将△ABC沿着AD折叠,点C落在AB边上.请用直尺和圆规作出点D(不写作法,保留作图痕迹);
(2)如图②,将△ABC沿着过点D的直线折叠,点C落在AB边上的E处.
①若DE⊥AB,垂足为E,请用直尺和圆规作出点D(不写作法,保留作图痕迹);
②若AB=4,BC=6,∠B=45°,则CD的取值范围是 .
答案:(1)如图所示:点D即为所求.
(2)①如图所示:点D即为所求.
②6-6≤CD≤5.
12.如图,a、b、c是三条互相平行的直线,点A在直线a上,请用尺规完成以下作图(不要求写作法,但要保留作图痕迹)
(1)作等腰直角△APQ,其中∠APQ=90°,P、Q都在直线c上(P在Q右侧);
(2)作等腰直角△AMN,其中∠AMN=90°,M、N分别在直线b、c上.
答案:(1)如图所示:△APQ即为所求.
(2)如图所示:△AMN即为所求.
13.(1)如图1,Rt△ABC中,∠B=90°,AB=2BC,现以C为圆心、CB长为半径画弧交边AC于D,再以A为圆心、AD为半径画弧交边AB于E.
求证:=.(这个比值叫做AE与AB的黄金比.)
(2)如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请你以图2中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.
(注:直尺没有刻度!作图不要求写作法,但要求保留作图痕迹,并对作图中涉及到的点用字母进行标注)
答案:(1)设BC=CD=x,则AB=2BC=2x.在Rt△ABC中,AB==x,∴AE=AD=AC-CD=(-1) x,∴=.
(2)如图所示:△ABF即为所求.
作AB的垂直平分线,交AB于D,过B作AB垂线,在垂线上截取BC=BD,连接AC,在AC上截取CE=BC,分别以A、B为圆心,AB、AE为半径画圆,交于点F.△ABF即为所求图形.
14、【缘起】苏教版九下P56,“如图1,在Rt△ABC中,∠ACB=90°,CD是△ABC的高,则△ACD与△CBD相似吗?”于是,学生甲发现CD2=AD·BD也成立.
问题1:请你证明CD2=AD·BD;
学生乙从CD2=AD·BD中得出:可以画出两条已知线段的比例中项.
证明:∵∠ACB=90°,CD是△ABC的高,∴∠ADC=∠CDB=90°,∵∠ACD+∠DCB=∠ACB=90°,∠ACD+∠A=90°,∴∠DCB=∠A,∴△ACD∽△CBD,∴=,∴CD2=AD·BD;
问题2:已知两条线段AB、BC在x轴上,如图2:请你用直尺(无刻度)和圆规作出这两条线段的比例中项.要求保留作图痕迹,不要写作法,最后指出所要作的线段.
答案:如图所示:线段DO即为所求.
学生丙也从CD2=AD·BD中悟出了矩形与正方形的等积作法.
问题3:如图3,已知矩形ABCD,请你用直尺(无刻度)和圆规作出一个正方形BMNP,使得S正方形BMNP=S矩形ABCD.要求:保留作图痕迹;简要写出作图每个步骤的要点.
答案:如图所示:四边形BMNP即为所求.
15.【回归课本】我们曾学习过这样的基本事实:①线段垂直平分线上的点到线段两端的距离相等;②同弧所对的圆周角相等.
【初步体验】如图,已知△ABC,用没有刻度的直尺和圆规作图,不要求写作法,但要保留作图痕迹,并对作图中涉及到的点用字母进行标注.
(1)在图1中AC边上找点D,使DB+DC=AC;
(2)在图2中作△BCE,使∠BEC=∠BAC,CE=BE.
答案:(1)如图所示:点D即为所求.
(2)如图所示:△BCE即为所求.
【深入探究】小明运用上述基本事实解决了下面一个问题:
(3)如图3,已知线段a和等边△ABC,作△BCM,使∠BMC=∠BAC,BM+CM=a.
他的做法是:
1画△ABC的外接圆;
2以A为圆心、AB长为半径画⊙A;
3以C为圆心、a为半径画弧与⊙A交于点F;
4连接CF与△ABC的外接圆交于点M,则△BCM是要画的三角形.
请你给出证明,并直接写出这样的点M有 个.
证明:连接BF.∵△ABC是等边三角形,∴∠BAC=60°,∴∠BMC=∠BAC=60°,∠BFC=∠BAC=30°,∴∠MBF=∠BMC-∠BFC=30°,∴∠MBF=∠BFC,∴MF=BM,∵MF+MC=FC=a,∴BM+MC=a.
如图所示:点M、M1、M2、M3为所求点,共4个.
(3)请你仿照小明的做法解决下面的问题:
如图4,已知线段b和△ABC,作△BCN,使∠BNC=∠BAC,BN-CN=b.
答案:作△ABC的外接圆,分别作∠ACB、∠ABC的平分线,交于点G,作△BCG的外接圆,以点B为圆心,b为半径交△BCG的外接圆于F,延长BF交△ABC的外接圆于点N,连接CN.则BN-CN=b.
同课章节目录
