中考培优第二轮复习专题 第7章 几何图形中的十字形学案(含答案)
文档属性
| 名称 | 中考培优第二轮复习专题 第7章 几何图形中的十字形学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 12:14:59 | ||
图片预览




文档简介
第七章 几何图形中的十字形
模型讲解
1、在正方形ABCD中,BN⊥AM,则常见的结论有哪些?
结论:
△ADM≌△BAN,AM=BN
2、在正方形ABCD中,E、F、G、H分别为AB、CD、BC、AD边上的点,若EF⊥GH,上述结论是否仍然成立?
【解析】
过点H作HN⊥BC,过点F作FM⊥AB
结论:
△ADM≌△BAN,AM=BN
所以大体上思路是“从垂直可利用全等推导出相等”
【思考】从相等是否可推导出垂直?
3、在正方形ABCD中,E、F、G、H分别为AB、CD、BC、AD边上的点,若EF=GH,则EF与GH不一定垂直,请画出反例.
如图,垂直只是相等时的一种情况,另一种,只需使得AH′=DH,BG′=CG′即可作出HG=H′G′
【模型拓展】
1°如图,在矩形ABCD中,AB=m,AD=n,在AD上有一点E,若CE⊥BD,则CE和BD之间有什么数量关系?
△CDE∽△BCD,==,即CE和BD之比等于矩形邻边之比
2°如图1,一般情况,在矩形ABCD中,E、F、G、H分别为AD、BC、AB、CD边上的点,当EF⊥GH时,有=的结论,证明方法如图2,证明△FME∽△GNH即可.
例题讲解
例题1、如图,将边长为4的正方形纸片ABCD折叠,使得点A落在CD的中点E处,折痕为FG,点F在AD边,求折痕FG的长;
【解析】
连接AE,由轴对称的性质可知,AE⊥FG(FG垂直平分AE)直接用上面的结论,由垂直得到相等,所以FG=AE==2.
例题2、如图,已知直线y=-x+2与x轴、y轴分别交于B、A两点,将△AOB沿着AB翻折,使点O落在点D上,当反比例函数y=经过点D时,求k的值.
【解析】
本题隐藏着“矩形内垂直”的模型,所以归根结底要往熟悉的题型上转化.
围成矩形,连接OD后,有OD⊥AB,
∴有==,OD和AB均可求出来
易求A(0,2),B(4,0)
所以AB=2,OD=2OG
在△ABO中,利用面积法可快速求出OG=,所以OD=,
∴==,∴ED=,OE=,D(,)
∴k=×=.
由于直角三角形可以看成是连接矩形对角线后分成的图形,所以矩形的结论可沿用至直角三角形内.
例题3、在Rt△ACB中,AC=4,BC=3,点D为AC上一点,连接BD,E为AB上一点,CE⊥BD,当AD=CD时,求AE的长.
【解析】
如图,补成矩形ACBH,延长CE交AH于点G,
有结论△BCD∽△CAG,所以==,
∴==,AG=,CG=,
再用一次X型相似即可,设CE=x,EG=-x,
有=,即=,解得x=,∴AE=.
【其它四边形中的十字】
例题4、如图,把边长为AB=2,BC=4且∠B=45°的平行四边形ABCD对折,使点B和D重合,求折痕MN的长.
【解析】
仍旧是转换为熟悉的模型呢?补成矩形就好了!
后面过程基本与前面例题一样
=,BD=2,DF=2,BF=6,
∴MN=.
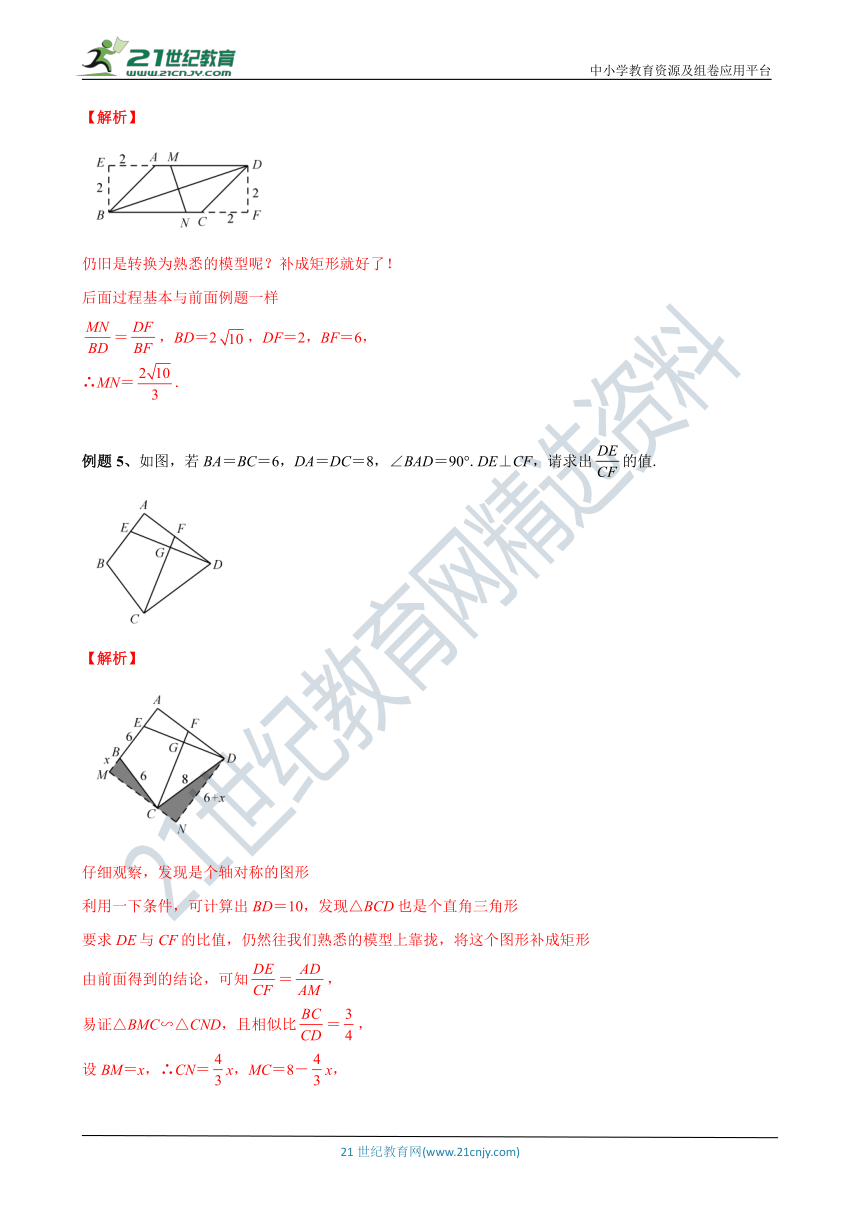
例题5、如图,若BA=BC=6,DA=DC=8,∠BAD=90°.DE⊥CF,请求出的值.
【解析】
仔细观察,发现是个轴对称的图形
利用一下条件,可计算出BD=10,发现△BCD也是个直角三角形
要求DE与CF的比值,仍然往我们熟悉的模型上靠拢,将这个图形补成矩形
由前面得到的结论,可知=,
易证△BMC∽△CND,且相似比=,
设BM=x,∴CN=x,MC=8-x,
∴=,即=,解得x=,∴AM=6+=
∴===.
模型讲解
1、如图把边长为AB=6,BC=8的矩形ABCD对折,使点B和D重合,求折痕MN的长.
答案:7.5
如图,作ME⊥BC,连接BD,则△MNE∽△DBA,∴=,即=,∴MN=7.5.
2、如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,求的值.
答案:
简析:设AF=x,则DF=EF=6-x,在Rt△AFE中,EF2=AF2+AE2,即(6-x)2=x2+32,
解得x=,∴DF=.
易证△FAE∽△EBG,∴BG=4,EG=5,∴GQ=1,
易证△EBG∽△HQG,∴QH=,∴CH=,∴==.
3、如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,=,△CEF的面积为S1,△AEB的面积为S2,则的值等于 .
答案:
简析:∵=,∴=,∴=,∴=()2=()2=.
4、如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
答案:B
简析:①过D作DM∥BE交AC于点N,交BC于点M,易证△AEF∽△CBF,故①正确;
②∵△AEF∽△CBF,∴CF=2AF,故②正确;
③易证四边形BMDE是平行四边形,BM=DE,M为BC的中点,∴N为CF的中点,∴DF=DC,故③正确;
④设AE=a,AB=b,则AD=2a,由△BAE∽△ADC,有=,即b=a,
∴tan∠CAD===,故④不正确;
故选B.
5、新定义:我们把两条中线互相垂直的三角形称为“中垂三角形”.如图所示,△ABC中,AF、BE是中线,且AF⊥BE,垂足为P,像△ABC这样的三角形称为“中垂三角形”,如果∠ABE=30°,AB=4,那么此时AC的长为 .
答案:2
解析:
连接EF,EFAB,则EF=2,由相似得PF=1,PE=,AE=,AC=2.
6、探究一:如图1,已知正方形ABCD,E、F分别是BC、AB上的两点,且AE⊥DF.小明经探究,发现AE=DF.请你帮他写出证明过程.
探究二:如图2,在矩形ABCD中,AB=3,BC=4,E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE⊥FH.小明发现,GE与FH并不相等,请你帮他求出的值.
探究三:小明思考这样一个问题:如图3,在正方形ABCD中,若E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE=FH,试问:GE⊥FH是否成立?若一定成立,请给予证明;若不一定成立,请画图并作出说明.
答案:
探究一:易证△ADF≌△BAE,∴AE=DF;
探究二:
如图,作GM⊥BC于点M,FN⊥CD于点N,则四边形FBCN、AGMB都是矩形,
∴FN=BC,GM=AB.
易证△FNH∽△GME,∴===;
探究三:
不一定成立,如图,当在GE时,GE和FH垂直,当在G′E′时,G′E′和FH就不垂直.
7、(1)如图,在Rt△ABC中,∠ABC=90°,点D为BC边上的点,BE⊥AD于点E,延长BE交AC于点F. ==1,求的值;
(2)在Rt△ABC中,∠ABC=90°,点D为直线BC上的动点(点D不与B、C重合),直线BE⊥AD于点E,交直线AC于点F.若==n,请探究并直接写出的所有可能的值(用含n的式子表示),不必证明.
答案:
(1)
如图,作CG⊥AD交AD的延长线于点G.
易证△BDE∽△ABE△ADB,得AB2=AD·AE,BD2=DE·DA,
∴= = =4,即AE=4DE.
易证△BDE≌△CDG,∴DE=DG=EG,即EG=2DE.
∵DG∥BF,∴== =2;
(2)点D是直线BC上的动点(点D不与B、C重合),有3种情况:
(i)当点D在线段BC上时,如图④,过点D作DG∥BF,交AC于点G.
∵==n,∴BD=nDC ,BC =(n+1)DC ,AB =n(n+1)DC.
∵DG∥BF,∴==n,∴FG=nGC ,FG=FC;
由(1)得AB2=AD·AE,BD2=DE·DA,
∴== =(n+1)2,
∵DG∥BF,∴==(n+1)2,即=(n+1)2,
化简得=n2+n;
(ii)当点D在线段BC的延长线上时,如图⑤,过点D作DG∥BE,交AC的延长线于点G.
同理可求得=n2-n;
(iii)当点D在线段CB的延长线上时,如图⑥,过点D作DG∥BF,交CA的延长线于点G.
同理可求得=n-n2.
8、【探究证明】
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证:=;
【结论应用】
(2)如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若=,则的值为 ;
【联系拓展】
(3)如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求的值.
答案:
(1)
如图,作AP∥EF,BQ∥GH,易证四边形AEFP、BHGQ都是平行四边形,∴AP=EF,GH=BQ.
由△PDA∽△QAB得=,∴=;
(2)∵EF⊥GH,AM⊥BN,∴由(1)中结论易得=,=,∴==;
(3)
如图,坐标为DS⊥BC易得S,AR⊥DS易得R,则四边形ABSR是矩形.
∵AM⊥DN,∴由(1)中结论可得=.
设SC=x(x>0),DS=y(y>0),则AR=BS=5+x,RD=10-y,
在Rt△CSD中,x2+y2=25 ①,
在Rt△ARD中,(5+x)2+(10-y)2=100 ②,
由②-①得x=2y-5 ③,
将③代入①得 x=3,y=5,
∴AR=5+x=8,∴===.
模型讲解
1、在正方形ABCD中,BN⊥AM,则常见的结论有哪些?
结论:
△ADM≌△BAN,AM=BN
2、在正方形ABCD中,E、F、G、H分别为AB、CD、BC、AD边上的点,若EF⊥GH,上述结论是否仍然成立?
【解析】
过点H作HN⊥BC,过点F作FM⊥AB
结论:
△ADM≌△BAN,AM=BN
所以大体上思路是“从垂直可利用全等推导出相等”
【思考】从相等是否可推导出垂直?
3、在正方形ABCD中,E、F、G、H分别为AB、CD、BC、AD边上的点,若EF=GH,则EF与GH不一定垂直,请画出反例.
如图,垂直只是相等时的一种情况,另一种,只需使得AH′=DH,BG′=CG′即可作出HG=H′G′
【模型拓展】
1°如图,在矩形ABCD中,AB=m,AD=n,在AD上有一点E,若CE⊥BD,则CE和BD之间有什么数量关系?
△CDE∽△BCD,==,即CE和BD之比等于矩形邻边之比
2°如图1,一般情况,在矩形ABCD中,E、F、G、H分别为AD、BC、AB、CD边上的点,当EF⊥GH时,有=的结论,证明方法如图2,证明△FME∽△GNH即可.
例题讲解
例题1、如图,将边长为4的正方形纸片ABCD折叠,使得点A落在CD的中点E处,折痕为FG,点F在AD边,求折痕FG的长;
【解析】
连接AE,由轴对称的性质可知,AE⊥FG(FG垂直平分AE)直接用上面的结论,由垂直得到相等,所以FG=AE==2.
例题2、如图,已知直线y=-x+2与x轴、y轴分别交于B、A两点,将△AOB沿着AB翻折,使点O落在点D上,当反比例函数y=经过点D时,求k的值.
【解析】
本题隐藏着“矩形内垂直”的模型,所以归根结底要往熟悉的题型上转化.
围成矩形,连接OD后,有OD⊥AB,
∴有==,OD和AB均可求出来
易求A(0,2),B(4,0)
所以AB=2,OD=2OG
在△ABO中,利用面积法可快速求出OG=,所以OD=,
∴==,∴ED=,OE=,D(,)
∴k=×=.
由于直角三角形可以看成是连接矩形对角线后分成的图形,所以矩形的结论可沿用至直角三角形内.
例题3、在Rt△ACB中,AC=4,BC=3,点D为AC上一点,连接BD,E为AB上一点,CE⊥BD,当AD=CD时,求AE的长.
【解析】
如图,补成矩形ACBH,延长CE交AH于点G,
有结论△BCD∽△CAG,所以==,
∴==,AG=,CG=,
再用一次X型相似即可,设CE=x,EG=-x,
有=,即=,解得x=,∴AE=.
【其它四边形中的十字】
例题4、如图,把边长为AB=2,BC=4且∠B=45°的平行四边形ABCD对折,使点B和D重合,求折痕MN的长.
【解析】
仍旧是转换为熟悉的模型呢?补成矩形就好了!
后面过程基本与前面例题一样
=,BD=2,DF=2,BF=6,
∴MN=.
例题5、如图,若BA=BC=6,DA=DC=8,∠BAD=90°.DE⊥CF,请求出的值.
【解析】
仔细观察,发现是个轴对称的图形
利用一下条件,可计算出BD=10,发现△BCD也是个直角三角形
要求DE与CF的比值,仍然往我们熟悉的模型上靠拢,将这个图形补成矩形
由前面得到的结论,可知=,
易证△BMC∽△CND,且相似比=,
设BM=x,∴CN=x,MC=8-x,
∴=,即=,解得x=,∴AM=6+=
∴===.
模型讲解
1、如图把边长为AB=6,BC=8的矩形ABCD对折,使点B和D重合,求折痕MN的长.
答案:7.5
如图,作ME⊥BC,连接BD,则△MNE∽△DBA,∴=,即=,∴MN=7.5.
2、如图,将边长为6cm的正方形ABCD折叠,使点D落在AB边的中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G,求的值.
答案:
简析:设AF=x,则DF=EF=6-x,在Rt△AFE中,EF2=AF2+AE2,即(6-x)2=x2+32,
解得x=,∴DF=.
易证△FAE∽△EBG,∴BG=4,EG=5,∴GQ=1,
易证△EBG∽△HQG,∴QH=,∴CH=,∴==.
3、如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,=,△CEF的面积为S1,△AEB的面积为S2,则的值等于 .
答案:
简析:∵=,∴=,∴=,∴=()2=()2=.
4、如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
答案:B
简析:①过D作DM∥BE交AC于点N,交BC于点M,易证△AEF∽△CBF,故①正确;
②∵△AEF∽△CBF,∴CF=2AF,故②正确;
③易证四边形BMDE是平行四边形,BM=DE,M为BC的中点,∴N为CF的中点,∴DF=DC,故③正确;
④设AE=a,AB=b,则AD=2a,由△BAE∽△ADC,有=,即b=a,
∴tan∠CAD===,故④不正确;
故选B.
5、新定义:我们把两条中线互相垂直的三角形称为“中垂三角形”.如图所示,△ABC中,AF、BE是中线,且AF⊥BE,垂足为P,像△ABC这样的三角形称为“中垂三角形”,如果∠ABE=30°,AB=4,那么此时AC的长为 .
答案:2
解析:
连接EF,EFAB,则EF=2,由相似得PF=1,PE=,AE=,AC=2.
6、探究一:如图1,已知正方形ABCD,E、F分别是BC、AB上的两点,且AE⊥DF.小明经探究,发现AE=DF.请你帮他写出证明过程.
探究二:如图2,在矩形ABCD中,AB=3,BC=4,E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE⊥FH.小明发现,GE与FH并不相等,请你帮他求出的值.
探究三:小明思考这样一个问题:如图3,在正方形ABCD中,若E、G分别在边BC、AD上,F、H分别在边AB、CD上,且GE=FH,试问:GE⊥FH是否成立?若一定成立,请给予证明;若不一定成立,请画图并作出说明.
答案:
探究一:易证△ADF≌△BAE,∴AE=DF;
探究二:
如图,作GM⊥BC于点M,FN⊥CD于点N,则四边形FBCN、AGMB都是矩形,
∴FN=BC,GM=AB.
易证△FNH∽△GME,∴===;
探究三:
不一定成立,如图,当在GE时,GE和FH垂直,当在G′E′时,G′E′和FH就不垂直.
7、(1)如图,在Rt△ABC中,∠ABC=90°,点D为BC边上的点,BE⊥AD于点E,延长BE交AC于点F. ==1,求的值;
(2)在Rt△ABC中,∠ABC=90°,点D为直线BC上的动点(点D不与B、C重合),直线BE⊥AD于点E,交直线AC于点F.若==n,请探究并直接写出的所有可能的值(用含n的式子表示),不必证明.
答案:
(1)
如图,作CG⊥AD交AD的延长线于点G.
易证△BDE∽△ABE△ADB,得AB2=AD·AE,BD2=DE·DA,
∴= = =4,即AE=4DE.
易证△BDE≌△CDG,∴DE=DG=EG,即EG=2DE.
∵DG∥BF,∴== =2;
(2)点D是直线BC上的动点(点D不与B、C重合),有3种情况:
(i)当点D在线段BC上时,如图④,过点D作DG∥BF,交AC于点G.
∵==n,∴BD=nDC ,BC =(n+1)DC ,AB =n(n+1)DC.
∵DG∥BF,∴==n,∴FG=nGC ,FG=FC;
由(1)得AB2=AD·AE,BD2=DE·DA,
∴== =(n+1)2,
∵DG∥BF,∴==(n+1)2,即=(n+1)2,
化简得=n2+n;
(ii)当点D在线段BC的延长线上时,如图⑤,过点D作DG∥BE,交AC的延长线于点G.
同理可求得=n2-n;
(iii)当点D在线段CB的延长线上时,如图⑥,过点D作DG∥BF,交CA的延长线于点G.
同理可求得=n-n2.
8、【探究证明】
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证:=;
【结论应用】
(2)如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若=,则的值为 ;
【联系拓展】
(3)如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求的值.
答案:
(1)
如图,作AP∥EF,BQ∥GH,易证四边形AEFP、BHGQ都是平行四边形,∴AP=EF,GH=BQ.
由△PDA∽△QAB得=,∴=;
(2)∵EF⊥GH,AM⊥BN,∴由(1)中结论易得=,=,∴==;
(3)
如图,坐标为DS⊥BC易得S,AR⊥DS易得R,则四边形ABSR是矩形.
∵AM⊥DN,∴由(1)中结论可得=.
设SC=x(x>0),DS=y(y>0),则AR=BS=5+x,RD=10-y,
在Rt△CSD中,x2+y2=25 ①,
在Rt△ARD中,(5+x)2+(10-y)2=100 ②,
由②-①得x=2y-5 ③,
将③代入①得 x=3,y=5,
∴AR=5+x=8,∴===.
同课章节目录
