中考培优第二轮复习专题 第18章 展开、缠绕、剪裁、拼接学案(含答案)
文档属性
| 名称 | 中考培优第二轮复习专题 第18章 展开、缠绕、剪裁、拼接学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 12:40:02 | ||
图片预览



文档简介
第十八章 展开、缠绕、剪裁、拼接
例题讲解
例题1、图1是由五个边长都是1的正方形纸片拼接而成的,过点A1的直线分别与BC1、BE交于点M、N,且图1被直线MN分成面积相等的上、下两部分.
图1 图2
(1)求CN+B1M的值;
(2)将图1沿虚线折成一个无盖的正方体纸盒(图2)后,求点M、N间的距离.
解:(1)∵A1B1∥BE,∴△A1B1M∽△NBM,∴,即,
∴MB+BN=MB?BN,∵图1被直线MN分成面积相等的上、下两部分,∴MB?BN5,∴MB?BN=5,即MB+BN=5,∴CN+B1M=5﹣4=1;
(2)连接MN,∵CN+B1M=1,∴EN=B1M,∴四边形BB1MN为矩形,∴MN=BB1=1.
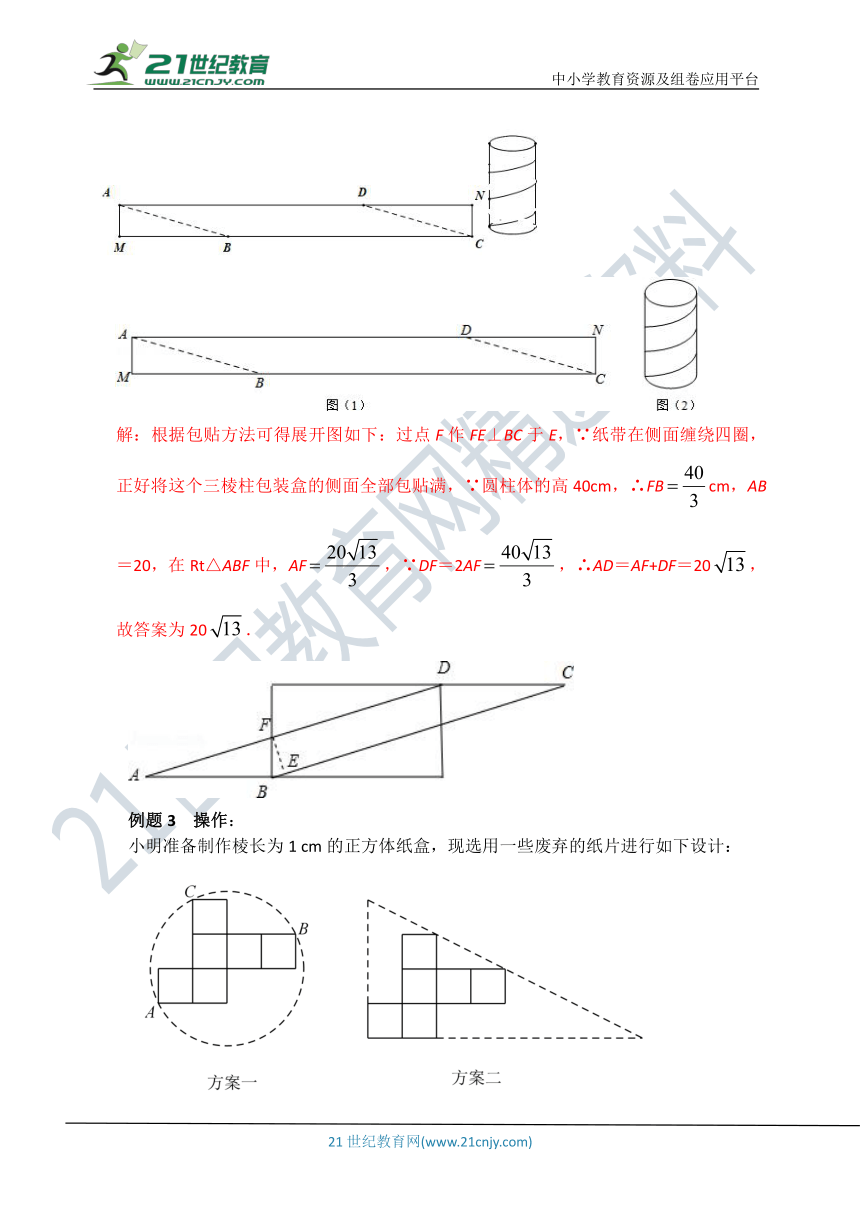
例题2、一个圆柱体包装盒,高40cm,底面周长20cm.现将彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图1),然后用这条平行四边形纸带按如图2的方式把这个圆柱体包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕四圈,正好将这个圆柱体包装盒的侧面全部包贴满,则所需的纸带AD的长度为 cm.
解:根据包贴方法可得展开图如下:过点F作FE⊥BC于E,∵纸带在侧面缠绕四圈,正好将这个三棱柱包装盒的侧面全部包贴满,∵圆柱体的高40cm,∴FBcm,AB=20,在Rt△ABF中,AF,∵DF=2AF,∴AD=AF+DF=20,
故答案为20.
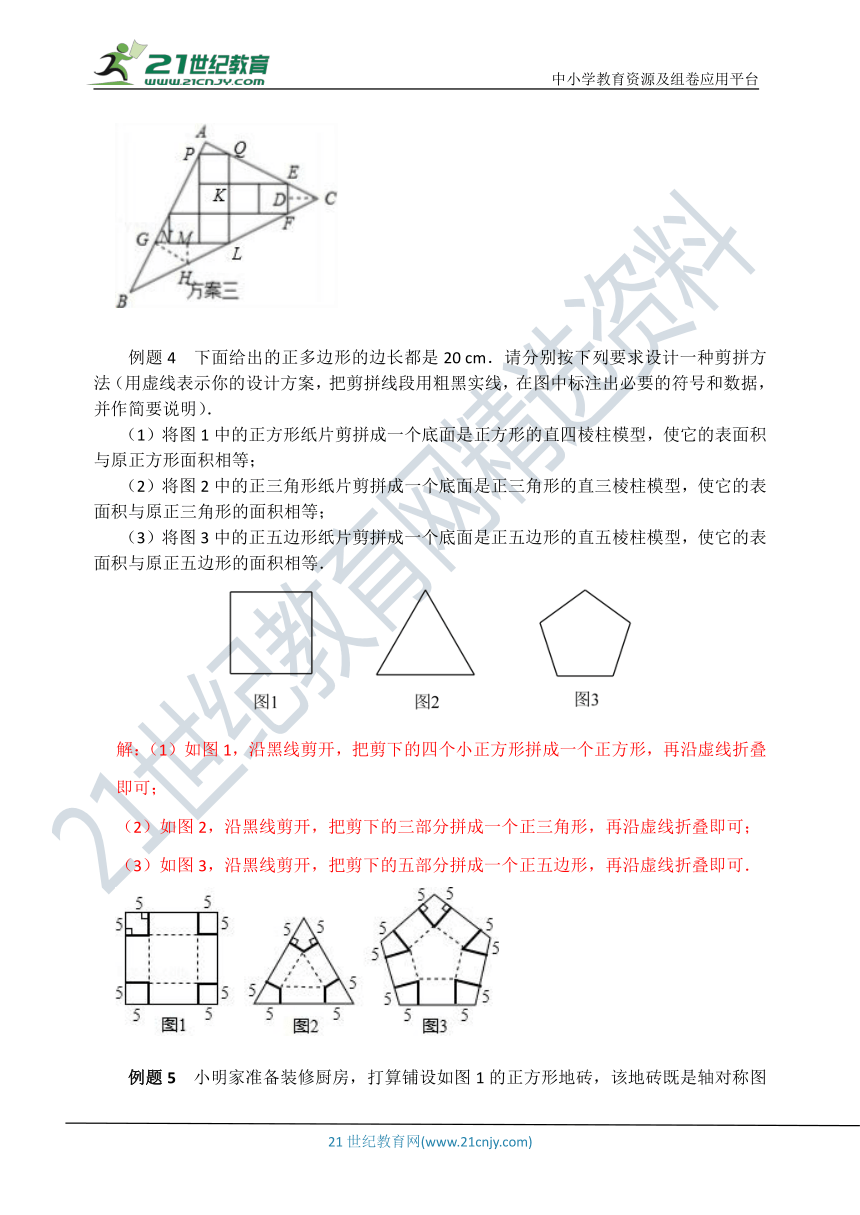
例题3 操作:
小明准备制作棱长为1 cm的正方体纸盒,现选用一些废弃的纸片进行如下设计:
说明:
方案一:图形中的圆过点A、B、C;
方案二:直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点.
纸片利用率=×100%
发现:
(1)小明发现方案一中的点A、B恰好为该圆一直径的两个端点.你认为小明的这个发现是否正确,请说明理由;
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写出求解过程.
探究:
(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.(方案三中的每条边均过其中两个正方形的顶点)
说明:
方案三中的每条边均过其中两个正方形的顶点.
解:发现:(1)小明的这个发现正确.理由:
解法一:如图一:连接AC、BC、AB,∵AC=BC,AB=2,∴AC2+BC2=AB2,∴∠BCA=90°,∴AB为该圆的直径.
解法二:如图二:连接AC、BC、AB.易证△AMC≌△BNC,∴∠ACM=∠CBN.
又∵∠BCN+∠CBN=90°,∴∠BCN+∠ACM=90°,即∠BCA=90°,∴AB为该圆的直径.
(2)如图三:∵DE=FH,DE∥FH,∴∠AED=∠EFH,∵∠ADE=∠EHF=90°,
∴△ADE≌△EHF(ASA),∴AD=EH=1.∵DE∥BC,∴△ADE∽△ACB,∴,∴,∴BC=8,∴S△ACB=16.∴该方案纸片利用率100%100%=37.5%;
探究:(3)过点C作CD⊥EF于D,过点G作GH∥AC,交BC于点H,
设AP=a,∵PQ∥EK,易得△APQ∽△KQE,△CEF是等腰三角形,△GHL是等腰三角形,∴AP:AQ=QK:EK=1:2,∴AQ=2a,PQa,∴EQ=5a,∵EC:ED=QE:QK,∴ECa,则PG=5aaa,GLa,∴GHa,∵,解得:GBa,∴ABa,ACa,∴S△ABCAB×ACa2,S展开图面积=6×5a2=30a2,
∴该方案纸片利用率100%100%=49.86%.
例题4 下面给出的正多边形的边长都是20 cm.请分别按下列要求设计一种剪拼方法(用虚线表示你的设计方案,把剪拼线段用粗黑实线,在图中标注出必要的符号和数据,并作简要说明).
(1)将图1中的正方形纸片剪拼成一个底面是正方形的直四棱柱模型,使它的表面积与原正方形面积相等;
(2)将图2中的正三角形纸片剪拼成一个底面是正三角形的直三棱柱模型,使它的表面积与原正三角形的面积相等;
(3)将图3中的正五边形纸片剪拼成一个底面是正五边形的直五棱柱模型,使它的表面积与原正五边形的面积相等.
解:(1)如图1,沿黑线剪开,把剪下的四个小正方形拼成一个正方形,再沿虚线折叠即可;
(2)如图2,沿黑线剪开,把剪下的三部分拼成一个正三角形,再沿虚线折叠即可;
(3)如图3,沿黑线剪开,把剪下的五部分拼成一个正五边形,再沿虚线折叠即可.
例题5 小明家准备装修厨房,打算铺设如图1的正方形地砖,该地砖既是轴对称图形也是中心对称图形,铺设效果如图2所示.经测量图1发现,砖面上四个小正方形的边长都是4 cm,AB=JN=2,中间的多边形CDEFGHIK是正八边形.
(1)求MA的长度;
(2)求正八边形CDEFGHIK的面积;
(3)已知小明家厨房的地面是边长为3.14米的正方形,用该地砖铺设完毕后,最多形成多少个正八边形?(地砖间缝隙的宽度忽略不计)
解:(1)连接BK和NC,两线的交点为O,∵四边形BCKN是正方形,∴∠NOB=90°,OB=ON,∵BN=4cm,∴由勾股定理得:BO=ON=2cm,∵JN=2cm,∴AM=JO=(2+2)cm;
(2)如图,作小正方形的对角线,组成正方形ORZQ,则正方形的边长为(24+2)cm,即为(44)cm,所以正八边形CDEFGHIK的面积为S正方形OQZR﹣4S△BOC=(44)2﹣422(32+32)cm2;
(3)正方形地砖的边长为:2×(2+2)cm+(44)cm=(8+8)cm,∵3.14米=314cm,∴3142÷(8+8)2≈264(块).答:用该地砖铺设完毕后,最多形成264个正八边形.
巩固练习
1.如图,正方体盒子的外表面上画有3条粗黑线,将这个正方体盒子的表面展开(外表面朝上),展开图可能是( )
【解析】解:根据正方体的表面展开图,两条黑线在一列,故A错误,且两条相邻成直角,故B错误,正视图的斜线方向相反,故C错误,只有D选项符合条件,故选D.
2.如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )
A.甲、乙都可以 B.甲、乙都不可以
C.甲不可以、乙可以 D.甲可以、乙不可以
【解析】解:所作图形如图所示,甲乙都可以拼一个与原来面积相等的正方形.故选A.
3.图1是一个八角星形纸板,图中有八个直角,八个相等的钝角,每条边都相等.如图2将纸板沿虚线进行切割,无缝隙无重叠的拼成图3所示的大正方形,其面积为8+4,则图3中线段AB的长为________.
【解析】解:设原八角形边长为a,则图2正方形边长为2aa、面积为(2aa)2,四个小三角形面积和为2a2,列式得(2aa)2+2a2=8+4,解得a=1,则AB=1.故答案为1.
4、如图,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非正方形).
(1)画出拼成的矩形的简图(请在简图上标明x与y);
(2)求的值.
【解析】解:(1)如图;(2)解:由拼图前后的面积相等得:[(x+y)+y]y=(x+y)2,
可得:x2+xy﹣y2=0,因为y≠0,再除以y2得到:解得:值不合题意,舍去).
5、“口子窖”酒的的包装底盒,是一个无盖的六棱柱形状的盒子(如图1),侧面是矩形或正方形.经测量,底面六边形有三条边的长是9 cm,有三条边的长是3 cm,每个内角都是120°,该六棱柱的高为3 cm.现沿它的侧棱剪开展平,得到如图2的平面展开图.
(1)制作这种底盒时,可以按图3中虚线裁剪出如图3的模片.现有一块长为17.5 cm、宽为16.5 cm的长方形铁皮,请问能否按图4的裁剪方法制作这样的无盖底盒?并请你说明理由;
(2)如果用一块正三角形铁皮按图4中虚线裁剪出如图3的模片,那么这个正三角形的边长至少应为________cm.(说明:以上裁剪均不计接缝处损耗)
【解答】解:(1)能.理由:如图所示,根据所构造的30度的直角三角形.图4中长方形的宽为:3+36+6.又因为66<16.5.长方形的长为:9+2()=12+3;又因为12+317.5.故长为17.5cm,宽为16.5cm的长方形铁皮,能按图4的裁剪方法制作这样的无盖底盒.
(2)如图所示,则等边三角形的边长是9+2(3+3)15.
6.动手实验:利用矩形纸片(如图1)剪出一个正六边形纸片:再利用这个正六边形纸片做一个无盖的正六棱柱(棱柱底面为正六边形),如图2.
(1)做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为多少?
(2)在(1)的条件下,当矩形的长为2a时,要使无盖正六棱柱侧面积最大,正六棱柱的高为多少?并求此时矩形纸片的利用率为多少?
(矩形纸片的利用率=)
【解答】解:(1)如图所示:由于正六边形内角和为(6﹣2)×180°=720°,则其一角的角平分线所分的两个角同为60°;设所需矩形的长宽分别为A、B,剪出的正六边形半径长为L,那么A=2L,B=2L?sin60°L;因此,所求长宽比为A:B=(2L):(L)=2:.做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为:2:;
(2)∵矩形的长为2a,宽为a,∴正六边形边长为a,其面积为S,设高为x,S=﹣4x2+6ax,当xa时,Sa2,此时,底面积a2,Sa2a2a2,故利用率.
7、【问题】如图1是底面半径都为1cm,母线长都为2cm的圆柱体和圆锥体模型.现要用如图2所示的长为2πcm,宽为4cm的长方形彩纸装饰圆柱、圆锥模型表面.已知一个圆柱和一个圆锥模型为一套,长方形彩纸共有122张,用这些长方形彩纸最多能装饰多少套模型呢?
【对话】
教师:“长方形彩纸可以怎样裁剪呢?”
学生甲:“可按图3方式裁剪出2张长方形.”
学生乙:“可按图4方式裁剪出6个小圆.”
学生丙:“可按图5方式裁剪出1个大圆和2个小圆.”
教师:“尽管还有其他裁剪方式,但为裁剪方便,我们就仅用这三位同学说的裁剪方法.”
【解决】
(1)计算:圆柱的侧面积是 cm2,圆锥的侧面积是 cm2:
(2)1张长方形彩纸剪拼后最多能装饰 个圆锥模型;5张长方形彩纸剪拼后最多能装饰 个圆柱模型;
(3)求用122张彩纸最多能装饰的圆锥、圆柱模型的套数.
答案:(1)圆柱的地面底面周长是2π,则圆柱的侧面积是2π×2=4πcm2,圆锥的侧面积是0.5×2π×2=2πcm2;
(2)圆柱的底面积是:πcm2,则圆柱的表面积是:6πcm2,圆锥的表面积是:3πcm2.
一张纸的面积是:4×2π=8π,则1张长方形彩纸剪拼后最多能装饰2个圆锥模型;5张长方形彩纸剪拼后最多能装饰6个圆柱体模型.
(3)设做x套模型,则每套模型中做圆锥的需x÷2张纸,作圆柱需要5x÷6张纸,
∴x÷2+5x÷6≤122,解得x≤91.5.
∵x是6的倍数,取x=90,做90套模型后剩余长方形纸片的张数是122-(45+75)=2张,
2张纸够做一套模型,∴最多能做91套模型.
8、如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图2中,计算裁剪的角度∠BAD;
(2)计算按图3方式包贴这个三棱柱包装盒所需的矩形纸带的长度.
答案:
(1)由图2的包贴方法知:AB的长等于三棱柱的底边周长,∴AB=30cm.
∵纸带的宽为15cm,∴sin∠BAD=sin∠ABM===,
∴∠BAD=30°;
(2)在图3中将三棱柱沿过点A的侧棱剪开,得知如图甲的侧面展开图.
将图甲的△ABF向左平移30cm,△CDE向右平移30cm,拼成如图乙中的平行四边形AMCN,此平行四边形即为图2中的平行四边形ABCD.
由题意得:图2中的BC=图乙中的AM=2AE=2AB÷cos∠EAB=60÷cos30°=40(cm).
故所需的矩形纸带的长度为MB+BC=30×cos30°+40=55cm.
9、如图1所示的纸杯,经测量(接缝处忽略不计),纸杯的杯口直径为7cm,底面直径为 cm,母线长为8cm,该纸杯的侧面展开如图2所示.
(1)求纸杯的侧面展开图2中杯口所在圆的半径OA的长;
(2)若一只小虫从纸杯底面的点C出发,沿纸杯侧面爬行一周(如图3)回到点A.求小虫爬行的最短路程.(精确到1cm)
(3)请你设计一种方案,在一张矩形纸片上能够剪出该纸杯的侧面,并求出你所设计的矩形的面积,要求:尽可能小.(精确到1cm)
答案:
(1)设∠O=n°,则7π=,=,解得OA=42,n=30°.
(2)
如图,沿CA剪开,得出扇形OAA′,连接CA′,则CA′的长度是小虫爬行的最短路程.
过C作CE⊥OA′于点E.
在Rt△COE中,OC=34,∠O=30°,∴CE=17,OE=17,∴A′E=42-17.
在Rt△CEA′中,CA′=≈21cm.
(3)
此方案设计的矩形的长约为21cm,宽约为10cm, 面积为21×10=210(cm2).
10、下面给出的三块正方形纸板的边长都是60cm,请分别按下列要求设计一种剪裁方法,折叠成一个礼品包装盒(纸板的厚度忽略不计).要求尽可能多地利用纸板,用虚线表示你的设计方案,并把剪裁线用实线标出.
(1)包装礼盒的六个面由六个矩形组成(如图1),请画出对应的设计图.
(2)包装礼盒的上盖由四个全等的等腰直角三角形组成(如图2),请画出对应的设计图.
(3)包装礼盒的上盖是双层的,由四个全等的矩形组成(如图3),请画出对应的设计图.
答案:如图所示:
(注:答案不唯一,不必考虑取最大值,只要不出现在中间扣一个图形即可,其他答案请相应给分)
11、在图1-5中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE=2b,且边AD和AE在同一直线上.
操作示例:
当2b<a时,如图1,在BA上选取点G,使BG=b,连接FG和CG,裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置构成四边形FGCH.
思考发现:
小明在操作后发现:该剪拼方法就是先将△FAG绕点F逆时针旋转90°到△FEH的位置,易知EH与AD在同一直线上.连接CH,由剪拼方法可得DH=BG,故△CHD≌△CGB,从而又可将△CGB绕点C顺时针旋转90°到△CHD的位置.这样,对于剪拼得到的四边形FGCH(如图1),过点F作FM⊥AE于点M(图略),利用SAS公理可判断△HFM≌△CHD,易得FH=HC=GC=FG,∠FHC=90°.进而根据正方形的判定方法,可以判断出四边形FGCH是正方形.
实践探究:
(1)正方形FGCH的面积是 ;(用含a,b的式子表示)
(2)类比图1的剪拼方法,请你就图2-图4的三种情形分别画出剪拼成一个新正方形的示意图.
联想拓展:
小明通过探究后发现:当b≤a时,此类图形都能剪拼成正方形,且所选取的点G的位置在BA方向上随着b的增大不断上移;当b>a时,如图5的图形能否剪拼成一个正方形?若能,请你在图中画出剪拼的示意图,若不能,简要说明理由.
答案:
实践探究:(1)a2+b2;
(2)剪拼方法如图3-图5.
联想拓展:能,剪拼方法如图6(图中BG=DH=b).
(注:图6用其它剪拼方法能拼接成面积为a2+b2的正方形均给分)
例题讲解
例题1、图1是由五个边长都是1的正方形纸片拼接而成的,过点A1的直线分别与BC1、BE交于点M、N,且图1被直线MN分成面积相等的上、下两部分.
图1 图2
(1)求CN+B1M的值;
(2)将图1沿虚线折成一个无盖的正方体纸盒(图2)后,求点M、N间的距离.
解:(1)∵A1B1∥BE,∴△A1B1M∽△NBM,∴,即,
∴MB+BN=MB?BN,∵图1被直线MN分成面积相等的上、下两部分,∴MB?BN5,∴MB?BN=5,即MB+BN=5,∴CN+B1M=5﹣4=1;
(2)连接MN,∵CN+B1M=1,∴EN=B1M,∴四边形BB1MN为矩形,∴MN=BB1=1.
例题2、一个圆柱体包装盒,高40cm,底面周长20cm.现将彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图1),然后用这条平行四边形纸带按如图2的方式把这个圆柱体包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕四圈,正好将这个圆柱体包装盒的侧面全部包贴满,则所需的纸带AD的长度为 cm.
解:根据包贴方法可得展开图如下:过点F作FE⊥BC于E,∵纸带在侧面缠绕四圈,正好将这个三棱柱包装盒的侧面全部包贴满,∵圆柱体的高40cm,∴FBcm,AB=20,在Rt△ABF中,AF,∵DF=2AF,∴AD=AF+DF=20,
故答案为20.
例题3 操作:
小明准备制作棱长为1 cm的正方体纸盒,现选用一些废弃的纸片进行如下设计:
说明:
方案一:图形中的圆过点A、B、C;
方案二:直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点.
纸片利用率=×100%
发现:
(1)小明发现方案一中的点A、B恰好为该圆一直径的两个端点.你认为小明的这个发现是否正确,请说明理由;
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写出求解过程.
探究:
(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.(方案三中的每条边均过其中两个正方形的顶点)
说明:
方案三中的每条边均过其中两个正方形的顶点.
解:发现:(1)小明的这个发现正确.理由:
解法一:如图一:连接AC、BC、AB,∵AC=BC,AB=2,∴AC2+BC2=AB2,∴∠BCA=90°,∴AB为该圆的直径.
解法二:如图二:连接AC、BC、AB.易证△AMC≌△BNC,∴∠ACM=∠CBN.
又∵∠BCN+∠CBN=90°,∴∠BCN+∠ACM=90°,即∠BCA=90°,∴AB为该圆的直径.
(2)如图三:∵DE=FH,DE∥FH,∴∠AED=∠EFH,∵∠ADE=∠EHF=90°,
∴△ADE≌△EHF(ASA),∴AD=EH=1.∵DE∥BC,∴△ADE∽△ACB,∴,∴,∴BC=8,∴S△ACB=16.∴该方案纸片利用率100%100%=37.5%;
探究:(3)过点C作CD⊥EF于D,过点G作GH∥AC,交BC于点H,
设AP=a,∵PQ∥EK,易得△APQ∽△KQE,△CEF是等腰三角形,△GHL是等腰三角形,∴AP:AQ=QK:EK=1:2,∴AQ=2a,PQa,∴EQ=5a,∵EC:ED=QE:QK,∴ECa,则PG=5aaa,GLa,∴GHa,∵,解得:GBa,∴ABa,ACa,∴S△ABCAB×ACa2,S展开图面积=6×5a2=30a2,
∴该方案纸片利用率100%100%=49.86%.
例题4 下面给出的正多边形的边长都是20 cm.请分别按下列要求设计一种剪拼方法(用虚线表示你的设计方案,把剪拼线段用粗黑实线,在图中标注出必要的符号和数据,并作简要说明).
(1)将图1中的正方形纸片剪拼成一个底面是正方形的直四棱柱模型,使它的表面积与原正方形面积相等;
(2)将图2中的正三角形纸片剪拼成一个底面是正三角形的直三棱柱模型,使它的表面积与原正三角形的面积相等;
(3)将图3中的正五边形纸片剪拼成一个底面是正五边形的直五棱柱模型,使它的表面积与原正五边形的面积相等.
解:(1)如图1,沿黑线剪开,把剪下的四个小正方形拼成一个正方形,再沿虚线折叠即可;
(2)如图2,沿黑线剪开,把剪下的三部分拼成一个正三角形,再沿虚线折叠即可;
(3)如图3,沿黑线剪开,把剪下的五部分拼成一个正五边形,再沿虚线折叠即可.
例题5 小明家准备装修厨房,打算铺设如图1的正方形地砖,该地砖既是轴对称图形也是中心对称图形,铺设效果如图2所示.经测量图1发现,砖面上四个小正方形的边长都是4 cm,AB=JN=2,中间的多边形CDEFGHIK是正八边形.
(1)求MA的长度;
(2)求正八边形CDEFGHIK的面积;
(3)已知小明家厨房的地面是边长为3.14米的正方形,用该地砖铺设完毕后,最多形成多少个正八边形?(地砖间缝隙的宽度忽略不计)
解:(1)连接BK和NC,两线的交点为O,∵四边形BCKN是正方形,∴∠NOB=90°,OB=ON,∵BN=4cm,∴由勾股定理得:BO=ON=2cm,∵JN=2cm,∴AM=JO=(2+2)cm;
(2)如图,作小正方形的对角线,组成正方形ORZQ,则正方形的边长为(24+2)cm,即为(44)cm,所以正八边形CDEFGHIK的面积为S正方形OQZR﹣4S△BOC=(44)2﹣422(32+32)cm2;
(3)正方形地砖的边长为:2×(2+2)cm+(44)cm=(8+8)cm,∵3.14米=314cm,∴3142÷(8+8)2≈264(块).答:用该地砖铺设完毕后,最多形成264个正八边形.
巩固练习
1.如图,正方体盒子的外表面上画有3条粗黑线,将这个正方体盒子的表面展开(外表面朝上),展开图可能是( )
【解析】解:根据正方体的表面展开图,两条黑线在一列,故A错误,且两条相邻成直角,故B错误,正视图的斜线方向相反,故C错误,只有D选项符合条件,故选D.
2.如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则( )
A.甲、乙都可以 B.甲、乙都不可以
C.甲不可以、乙可以 D.甲可以、乙不可以
【解析】解:所作图形如图所示,甲乙都可以拼一个与原来面积相等的正方形.故选A.
3.图1是一个八角星形纸板,图中有八个直角,八个相等的钝角,每条边都相等.如图2将纸板沿虚线进行切割,无缝隙无重叠的拼成图3所示的大正方形,其面积为8+4,则图3中线段AB的长为________.
【解析】解:设原八角形边长为a,则图2正方形边长为2aa、面积为(2aa)2,四个小三角形面积和为2a2,列式得(2aa)2+2a2=8+4,解得a=1,则AB=1.故答案为1.
4、如图,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非正方形).
(1)画出拼成的矩形的简图(请在简图上标明x与y);
(2)求的值.
【解析】解:(1)如图;(2)解:由拼图前后的面积相等得:[(x+y)+y]y=(x+y)2,
可得:x2+xy﹣y2=0,因为y≠0,再除以y2得到:解得:值不合题意,舍去).
5、“口子窖”酒的的包装底盒,是一个无盖的六棱柱形状的盒子(如图1),侧面是矩形或正方形.经测量,底面六边形有三条边的长是9 cm,有三条边的长是3 cm,每个内角都是120°,该六棱柱的高为3 cm.现沿它的侧棱剪开展平,得到如图2的平面展开图.
(1)制作这种底盒时,可以按图3中虚线裁剪出如图3的模片.现有一块长为17.5 cm、宽为16.5 cm的长方形铁皮,请问能否按图4的裁剪方法制作这样的无盖底盒?并请你说明理由;
(2)如果用一块正三角形铁皮按图4中虚线裁剪出如图3的模片,那么这个正三角形的边长至少应为________cm.(说明:以上裁剪均不计接缝处损耗)
【解答】解:(1)能.理由:如图所示,根据所构造的30度的直角三角形.图4中长方形的宽为:3+36+6.又因为66<16.5.长方形的长为:9+2()=12+3;又因为12+317.5.故长为17.5cm,宽为16.5cm的长方形铁皮,能按图4的裁剪方法制作这样的无盖底盒.
(2)如图所示,则等边三角形的边长是9+2(3+3)15.
6.动手实验:利用矩形纸片(如图1)剪出一个正六边形纸片:再利用这个正六边形纸片做一个无盖的正六棱柱(棱柱底面为正六边形),如图2.
(1)做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为多少?
(2)在(1)的条件下,当矩形的长为2a时,要使无盖正六棱柱侧面积最大,正六棱柱的高为多少?并求此时矩形纸片的利用率为多少?
(矩形纸片的利用率=)
【解答】解:(1)如图所示:由于正六边形内角和为(6﹣2)×180°=720°,则其一角的角平分线所分的两个角同为60°;设所需矩形的长宽分别为A、B,剪出的正六边形半径长为L,那么A=2L,B=2L?sin60°L;因此,所求长宽比为A:B=(2L):(L)=2:.做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为:2:;
(2)∵矩形的长为2a,宽为a,∴正六边形边长为a,其面积为S,设高为x,S=﹣4x2+6ax,当xa时,Sa2,此时,底面积a2,Sa2a2a2,故利用率.
7、【问题】如图1是底面半径都为1cm,母线长都为2cm的圆柱体和圆锥体模型.现要用如图2所示的长为2πcm,宽为4cm的长方形彩纸装饰圆柱、圆锥模型表面.已知一个圆柱和一个圆锥模型为一套,长方形彩纸共有122张,用这些长方形彩纸最多能装饰多少套模型呢?
【对话】
教师:“长方形彩纸可以怎样裁剪呢?”
学生甲:“可按图3方式裁剪出2张长方形.”
学生乙:“可按图4方式裁剪出6个小圆.”
学生丙:“可按图5方式裁剪出1个大圆和2个小圆.”
教师:“尽管还有其他裁剪方式,但为裁剪方便,我们就仅用这三位同学说的裁剪方法.”
【解决】
(1)计算:圆柱的侧面积是 cm2,圆锥的侧面积是 cm2:
(2)1张长方形彩纸剪拼后最多能装饰 个圆锥模型;5张长方形彩纸剪拼后最多能装饰 个圆柱模型;
(3)求用122张彩纸最多能装饰的圆锥、圆柱模型的套数.
答案:(1)圆柱的地面底面周长是2π,则圆柱的侧面积是2π×2=4πcm2,圆锥的侧面积是0.5×2π×2=2πcm2;
(2)圆柱的底面积是:πcm2,则圆柱的表面积是:6πcm2,圆锥的表面积是:3πcm2.
一张纸的面积是:4×2π=8π,则1张长方形彩纸剪拼后最多能装饰2个圆锥模型;5张长方形彩纸剪拼后最多能装饰6个圆柱体模型.
(3)设做x套模型,则每套模型中做圆锥的需x÷2张纸,作圆柱需要5x÷6张纸,
∴x÷2+5x÷6≤122,解得x≤91.5.
∵x是6的倍数,取x=90,做90套模型后剩余长方形纸片的张数是122-(45+75)=2张,
2张纸够做一套模型,∴最多能做91套模型.
8、如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.
(1)请在图2中,计算裁剪的角度∠BAD;
(2)计算按图3方式包贴这个三棱柱包装盒所需的矩形纸带的长度.
答案:
(1)由图2的包贴方法知:AB的长等于三棱柱的底边周长,∴AB=30cm.
∵纸带的宽为15cm,∴sin∠BAD=sin∠ABM===,
∴∠BAD=30°;
(2)在图3中将三棱柱沿过点A的侧棱剪开,得知如图甲的侧面展开图.
将图甲的△ABF向左平移30cm,△CDE向右平移30cm,拼成如图乙中的平行四边形AMCN,此平行四边形即为图2中的平行四边形ABCD.
由题意得:图2中的BC=图乙中的AM=2AE=2AB÷cos∠EAB=60÷cos30°=40(cm).
故所需的矩形纸带的长度为MB+BC=30×cos30°+40=55cm.
9、如图1所示的纸杯,经测量(接缝处忽略不计),纸杯的杯口直径为7cm,底面直径为 cm,母线长为8cm,该纸杯的侧面展开如图2所示.
(1)求纸杯的侧面展开图2中杯口所在圆的半径OA的长;
(2)若一只小虫从纸杯底面的点C出发,沿纸杯侧面爬行一周(如图3)回到点A.求小虫爬行的最短路程.(精确到1cm)
(3)请你设计一种方案,在一张矩形纸片上能够剪出该纸杯的侧面,并求出你所设计的矩形的面积,要求:尽可能小.(精确到1cm)
答案:
(1)设∠O=n°,则7π=,=,解得OA=42,n=30°.
(2)
如图,沿CA剪开,得出扇形OAA′,连接CA′,则CA′的长度是小虫爬行的最短路程.
过C作CE⊥OA′于点E.
在Rt△COE中,OC=34,∠O=30°,∴CE=17,OE=17,∴A′E=42-17.
在Rt△CEA′中,CA′=≈21cm.
(3)
此方案设计的矩形的长约为21cm,宽约为10cm, 面积为21×10=210(cm2).
10、下面给出的三块正方形纸板的边长都是60cm,请分别按下列要求设计一种剪裁方法,折叠成一个礼品包装盒(纸板的厚度忽略不计).要求尽可能多地利用纸板,用虚线表示你的设计方案,并把剪裁线用实线标出.
(1)包装礼盒的六个面由六个矩形组成(如图1),请画出对应的设计图.
(2)包装礼盒的上盖由四个全等的等腰直角三角形组成(如图2),请画出对应的设计图.
(3)包装礼盒的上盖是双层的,由四个全等的矩形组成(如图3),请画出对应的设计图.
答案:如图所示:
(注:答案不唯一,不必考虑取最大值,只要不出现在中间扣一个图形即可,其他答案请相应给分)
11、在图1-5中,正方形ABCD的边长为a,等腰直角三角形FAE的斜边AE=2b,且边AD和AE在同一直线上.
操作示例:
当2b<a时,如图1,在BA上选取点G,使BG=b,连接FG和CG,裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置构成四边形FGCH.
思考发现:
小明在操作后发现:该剪拼方法就是先将△FAG绕点F逆时针旋转90°到△FEH的位置,易知EH与AD在同一直线上.连接CH,由剪拼方法可得DH=BG,故△CHD≌△CGB,从而又可将△CGB绕点C顺时针旋转90°到△CHD的位置.这样,对于剪拼得到的四边形FGCH(如图1),过点F作FM⊥AE于点M(图略),利用SAS公理可判断△HFM≌△CHD,易得FH=HC=GC=FG,∠FHC=90°.进而根据正方形的判定方法,可以判断出四边形FGCH是正方形.
实践探究:
(1)正方形FGCH的面积是 ;(用含a,b的式子表示)
(2)类比图1的剪拼方法,请你就图2-图4的三种情形分别画出剪拼成一个新正方形的示意图.
联想拓展:
小明通过探究后发现:当b≤a时,此类图形都能剪拼成正方形,且所选取的点G的位置在BA方向上随着b的增大不断上移;当b>a时,如图5的图形能否剪拼成一个正方形?若能,请你在图中画出剪拼的示意图,若不能,简要说明理由.
答案:
实践探究:(1)a2+b2;
(2)剪拼方法如图3-图5.
联想拓展:能,剪拼方法如图6(图中BG=DH=b).
(注:图6用其它剪拼方法能拼接成面积为a2+b2的正方形均给分)
同课章节目录
