2.3.1 直线与平面垂直的判定 课件 26张PPT
文档属性
| 名称 | 2.3.1 直线与平面垂直的判定 课件 26张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 11:54:28 | ||
图片预览




文档简介
(共26张PPT)
2.3.1直线与平面垂直的判定
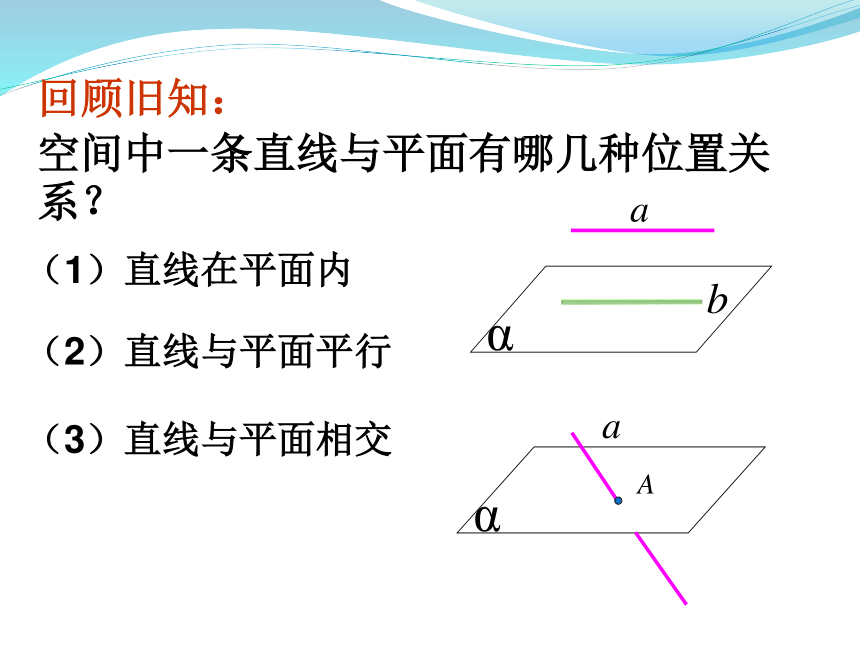
回顾旧知:
空间中一条直线与平面有哪几种位置关系?
(3)直线与平面相交
(1)直线在平面内
(2)直线与平面平行
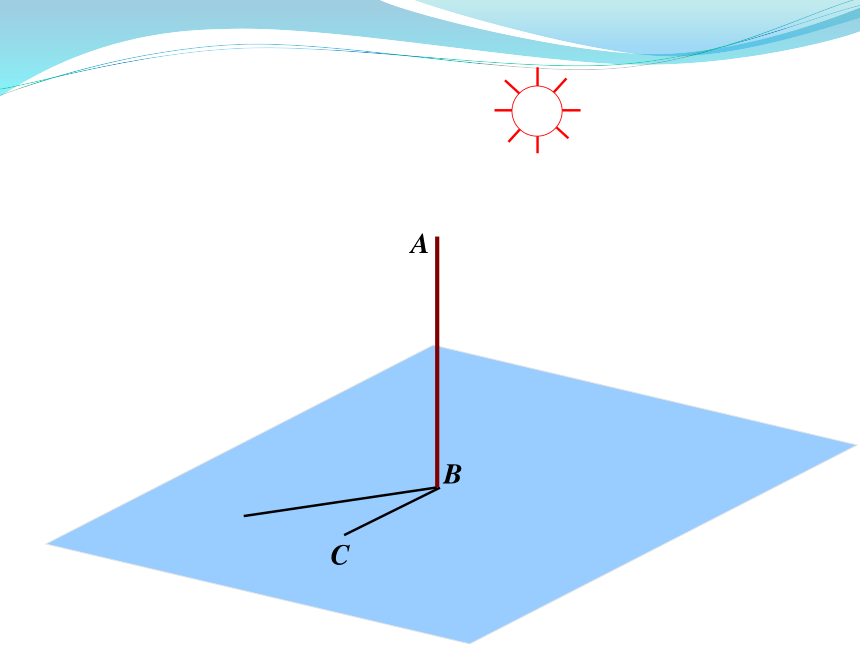
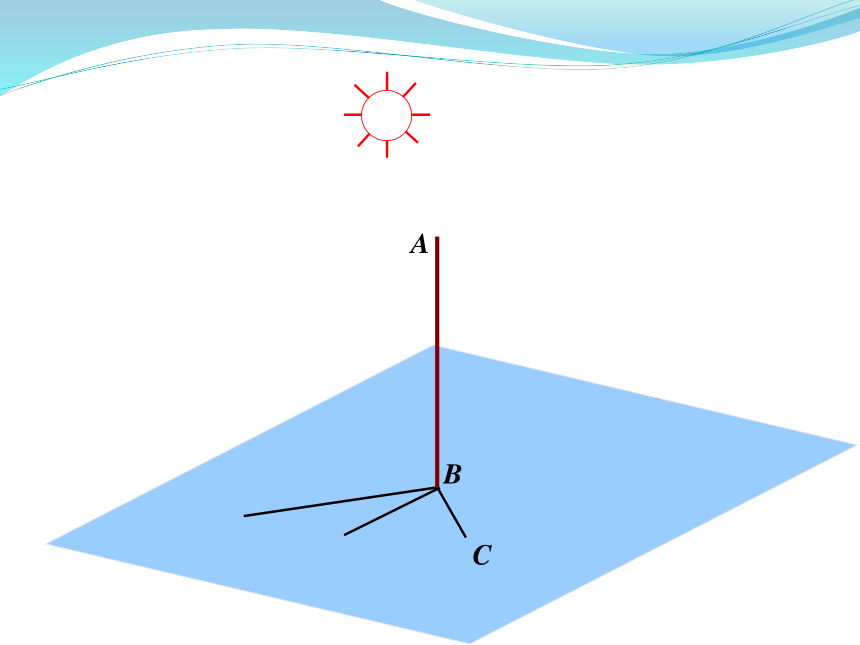
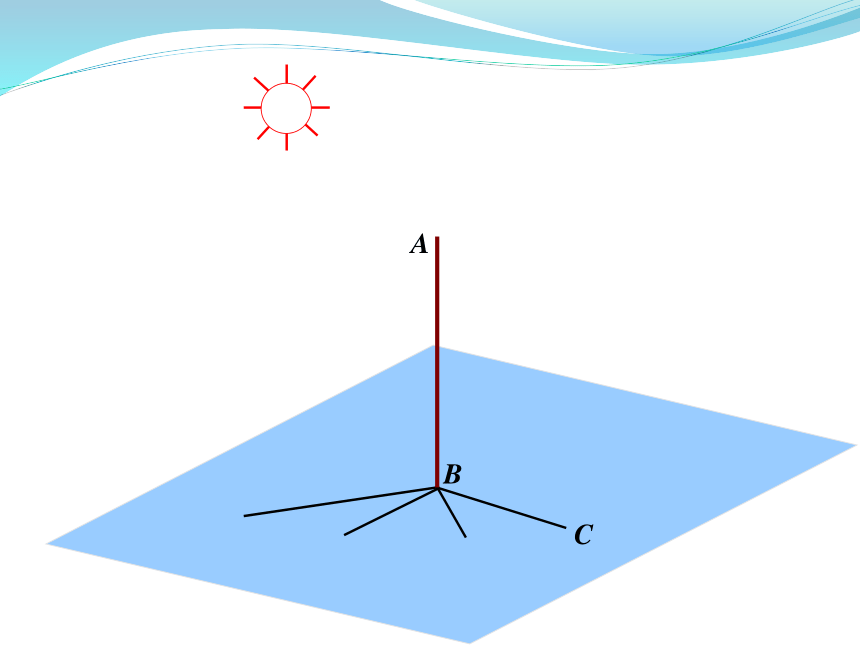
知识探究(一):直线与平面垂直的概念
旗杆与地面的关系,给人以直线与平面垂直的形象。
大桥的桥柱与水面的位置关系,给人以直线与平面垂直的形象。
C
思考:如何定义一条直线
与一个平面垂直?
C
C
C
α
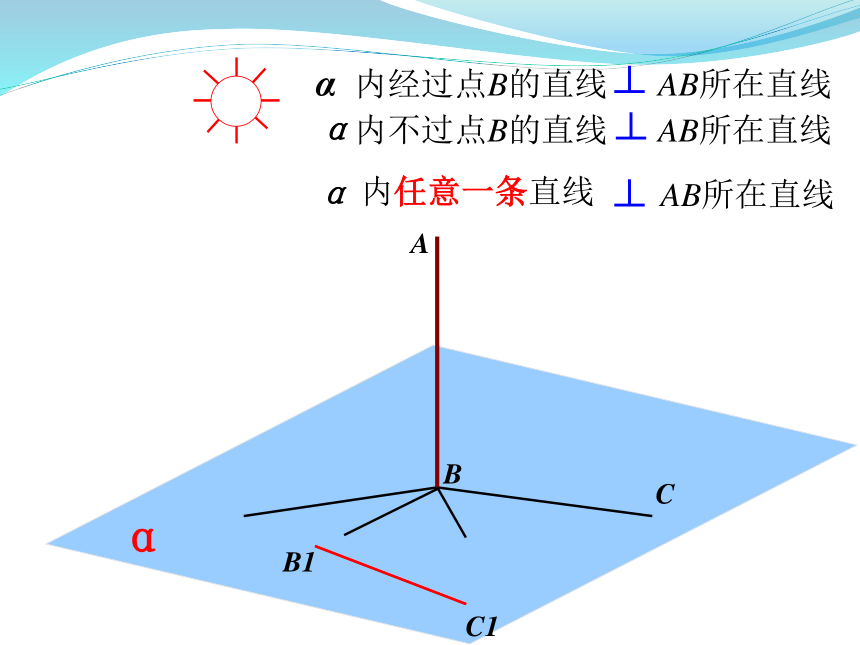
内经过点B的直线
AB所在直线
内不过点B的直线
α
α
AB所在直线
内任意一条直线
α
AB所在直线
⊥
⊥
⊥
C
B1
C1
直线与平面垂直的定义:
深入理解“线面垂直定义”
判断下列语句是否正确:(若不正确请举反例)
1.如果一条直线与一个平面垂直,那么它与平面内所有的直线都垂直. ( )
2.如果一条直线与平面内无数条直线都垂直,那么它与平面垂直. ( )
知识探究(二):直线与平面垂直的判定定理
思考:是否把平面中的直线一一找出,才能
证明直线与平面垂直?
探究活动:请同学们拿出一块三角形的纸片,做以下试验:
过△ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触).
(1)折痕AD与桌面垂直吗?
(2)如何翻折才能保证折痕AD与桌面所在平面肯定垂直?
结论:AD⊥BD,AD⊥CD,BD∩CD=D,
有AD⊥α.
直线与平面垂直的判定定理:
一条直线和一个平面内的两条相交直线都垂直,则这条直线垂直于这个平面.
线线垂直 线面垂直
关键:线不在多,相交则行
例1.如图,已知OA、OB、OC 两两垂直
(1)求证:OA⊥平面OBC
(2)求证:OA⊥BC
B
C
O
A
例题示范,巩固新知
变式训练:一旗杆高8m,在它的顶点处系两条长10m的绳子,拉紧绳子并把它们的下端固定在地面上的两点(与旗杆脚不在同一条直线上)。如果这两点与旗杆脚距6m,那么旗杆就与地面垂直,为什么?
例2.在下图的长方体中,请列举与平面ABCD垂直的直线。并说明这些直线有怎样的位置关系?
变式:在正方体ABCD-A1B1C1D1 中,与AD1 垂直的平面是(????? ) A.平面 DD1C1C
B.平面A1DCB1 C.平面A1B1C1D1
D.平面 A1DB
例3.如图,已知a∥b、a⊥α.
求证:b⊥α.
例题示范,巩固新知
练习:
1.如图,在三棱锥V-ABC中 ,VA=VC,
AB=BC,K是AC的中点.
求证:AC⊥平面VKB.
变式:
在练习1.中若E、F分别为AB、BC 的中点,试判断EF与平面VKB的位置关系.
思考:图中有几个直角三角形?由此你认为三棱锥中最多有几个直角三角形?
3: 已知 , 于 ,
,求证: .
于
比比谁最棒!!!
1.直线与平面垂直的定义
3.数学思想方法:转化的思想
知识小结
2.直线与平面垂直的判定
线线垂直
线面垂直
布置作业—自主探究
作业:P74??B组2,4题
2.3.1直线与平面垂直的判定
回顾旧知:
空间中一条直线与平面有哪几种位置关系?
(3)直线与平面相交
(1)直线在平面内
(2)直线与平面平行
知识探究(一):直线与平面垂直的概念
旗杆与地面的关系,给人以直线与平面垂直的形象。
大桥的桥柱与水面的位置关系,给人以直线与平面垂直的形象。
C
思考:如何定义一条直线
与一个平面垂直?
C
C
C
α
内经过点B的直线
AB所在直线
内不过点B的直线
α
α
AB所在直线
内任意一条直线
α
AB所在直线
⊥
⊥
⊥
C
B1
C1
直线与平面垂直的定义:
深入理解“线面垂直定义”
判断下列语句是否正确:(若不正确请举反例)
1.如果一条直线与一个平面垂直,那么它与平面内所有的直线都垂直. ( )
2.如果一条直线与平面内无数条直线都垂直,那么它与平面垂直. ( )
知识探究(二):直线与平面垂直的判定定理
思考:是否把平面中的直线一一找出,才能
证明直线与平面垂直?
探究活动:请同学们拿出一块三角形的纸片,做以下试验:
过△ABC的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触).
(1)折痕AD与桌面垂直吗?
(2)如何翻折才能保证折痕AD与桌面所在平面肯定垂直?
结论:AD⊥BD,AD⊥CD,BD∩CD=D,
有AD⊥α.
直线与平面垂直的判定定理:
一条直线和一个平面内的两条相交直线都垂直,则这条直线垂直于这个平面.
线线垂直 线面垂直
关键:线不在多,相交则行
例1.如图,已知OA、OB、OC 两两垂直
(1)求证:OA⊥平面OBC
(2)求证:OA⊥BC
B
C
O
A
例题示范,巩固新知
变式训练:一旗杆高8m,在它的顶点处系两条长10m的绳子,拉紧绳子并把它们的下端固定在地面上的两点(与旗杆脚不在同一条直线上)。如果这两点与旗杆脚距6m,那么旗杆就与地面垂直,为什么?
例2.在下图的长方体中,请列举与平面ABCD垂直的直线。并说明这些直线有怎样的位置关系?
变式:在正方体ABCD-A1B1C1D1 中,与AD1 垂直的平面是(????? ) A.平面 DD1C1C
B.平面A1DCB1 C.平面A1B1C1D1
D.平面 A1DB
例3.如图,已知a∥b、a⊥α.
求证:b⊥α.
例题示范,巩固新知
练习:
1.如图,在三棱锥V-ABC中 ,VA=VC,
AB=BC,K是AC的中点.
求证:AC⊥平面VKB.
变式:
在练习1.中若E、F分别为AB、BC 的中点,试判断EF与平面VKB的位置关系.
思考:图中有几个直角三角形?由此你认为三棱锥中最多有几个直角三角形?
3: 已知 , 于 ,
,求证: .
于
比比谁最棒!!!
1.直线与平面垂直的定义
3.数学思想方法:转化的思想
知识小结
2.直线与平面垂直的判定
线线垂直
线面垂直
布置作业—自主探究
作业:P74??B组2,4题
