2.3.1 直线与平面垂直的判定 课件 25张PPT
文档属性
| 名称 | 2.3.1 直线与平面垂直的判定 课件 25张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-07 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
*
学习目标:
1.理解直线与平面垂直的定义;
2.掌握直线与平面垂直的判定定理及应用;
3.应用直线与平面垂直的判定定理解决问题;
重点:操作确认并概括出直线与平面垂直的定义和判定定理.
难点:操作确认并概括出直线与平面垂直的判定定理及初步运用.
*
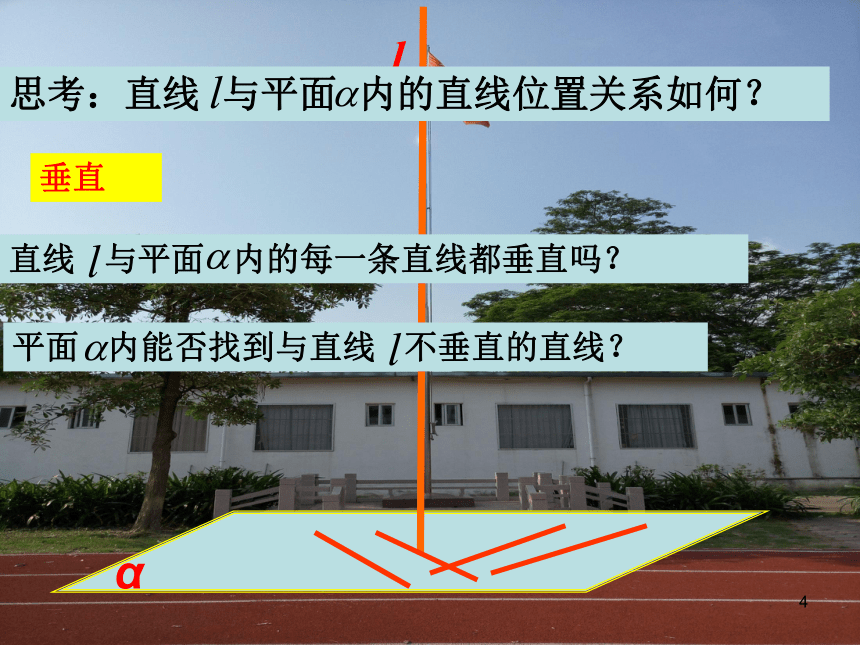
说说它们的位置关系
旗杆与地面:
宿舍楼前的柱子与地面:
桥墩与水面:
垂直
*
l
α
垂直
*
l
α
垂直
尝试概括直线与平面垂直的概念
*
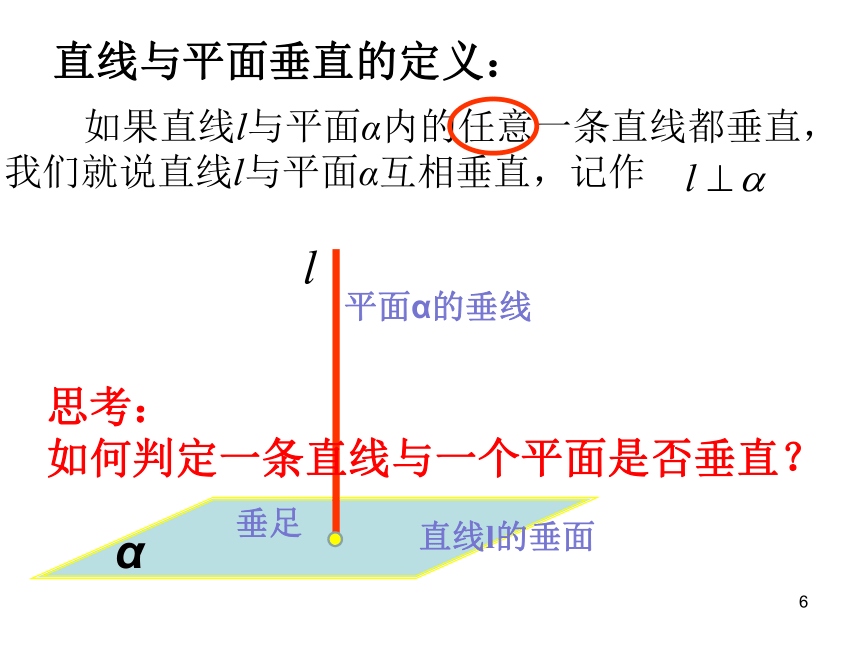
直线与平面垂直的定义:
如果直线l与平面α内的任意一条直线都垂直,我们就说直线l与平面α互相垂直,记作
平面α的垂线
直线l的垂面
垂足
思考:
如何判定一条直线与一个平面是否垂直?
*
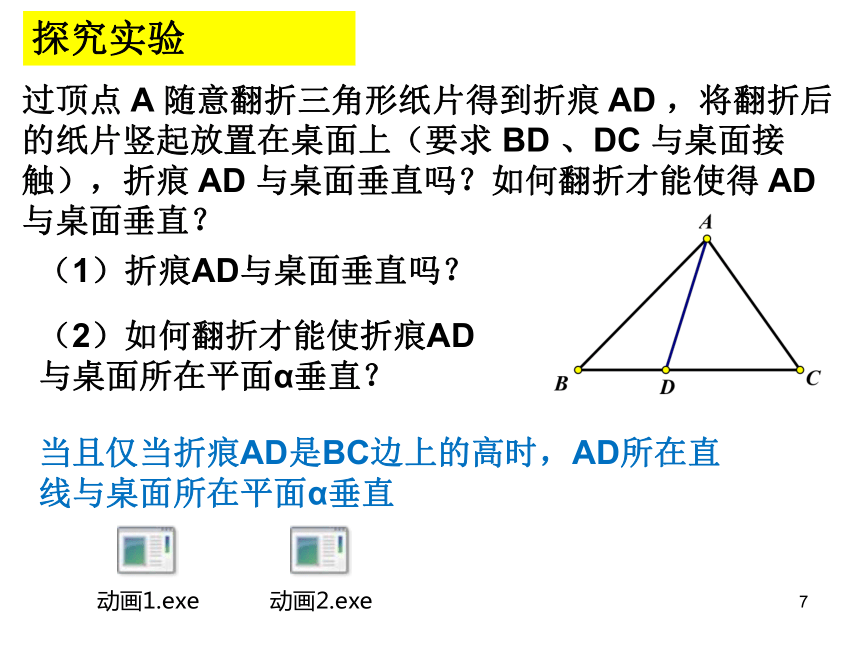
探究实验
过顶点 A 随意翻折三角形纸片得到折痕 AD ,将翻折后的纸片竖起放置在桌面上(要求 BD 、DC 与桌面接触),折痕 AD 与桌面垂直吗?如何翻折才能使得 AD 与桌面垂直?
(1)折痕AD与桌面垂直吗?
(2)如何翻折才能使折痕AD与桌面所在平面α垂直?
当且仅当折痕AD是BC边上的高时,AD所在直线与桌面所在平面α垂直
*
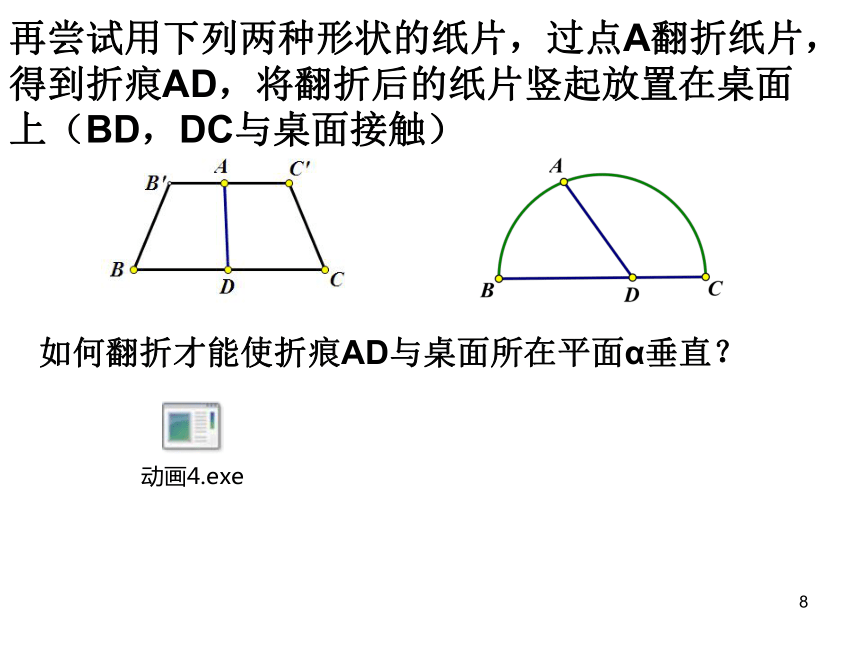
再尝试用下列两种形状的纸片,过点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD,DC与桌面接触)
如何翻折才能使折痕AD与桌面所在平面α垂直?
*
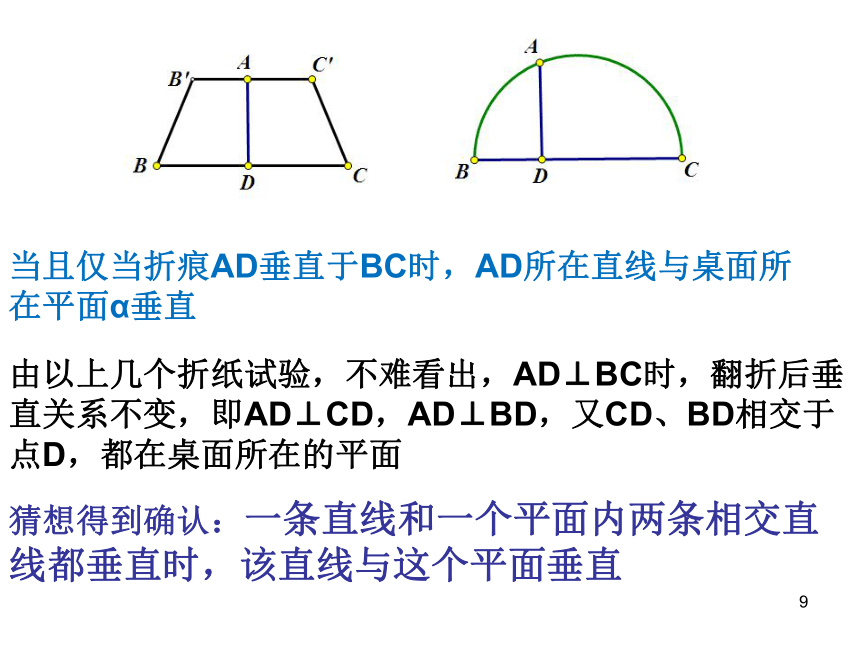
当且仅当折痕AD垂直于BC时,AD所在直线与桌面所在平面α垂直
由以上几个折纸试验,不难看出,AD⊥BC时,翻折后垂直关系不变,即AD⊥CD,AD⊥BD,又CD、BD相交于点D,都在桌面所在的平面
猜想得到确认:一条直线和一个平面内两条相交直线都垂直时,该直线与这个平面垂直
*
直线与平面垂直的判定定理:
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直
符号表示:
P
*
预习自测:
1.判断下列说法正确的是:
①若 l⊥α,a?α,则 l⊥a;
②若 a⊥l,a//b,则 b⊥l;
③若直线 l 垂直于平面α内的无数条直线,则 l⊥α;
④若直线 l 垂直于平面α,则 l 与α内的直线可相交,可异面,可平行
①②
*
预习自测:
2.在正方体 ABCD-A1B1C1D1中,
与平面 ABCD 垂直的直线
有____________
与直线 A1A 垂直的平面
有____________
与直线 A1A 垂直的直线
有____________
AA1,BB1,CC1,DD1
平面ABCD,平面A1B1C1D1
AB,BC,CD,DA,A1B1,B1C1,C1D1,D1A1
*
探究案
例题 1 如图,在三棱锥V-ABC中,VA=VC,AB=BC,O为AC的中点,求证:AC⊥平面VOB.
书写过程要求:
①字迹工整清晰;
②每一步骤的依据要表达清楚;
③推出直线与平面垂直的条件缺一不可.
*
探究案
例题 1 如图,在三棱锥V-ABC中,VA=VC,AB=BC,O为AC的中点,求证:AC⊥平面VOB.
*
探究案:
例2.正方体ABCD-A1B1C1D1 中,
求证: BD⊥平面ACC1A1
书写过程要求:
①字迹工整清晰;
②每一步骤的依据要表达清楚;
③推出直线与平面垂直的条件缺一不可.
*
定理应用:
例2.正方体ABCD-A1B1C1D1 中,
求证: BD⊥平面ACC1A1
证明:
因为四边形ABCD是正方形,所以BD⊥AC,
*
变式:在底面为菱形的直棱柱
ABCD-A1B1C1D1 中,
求证: BD⊥平面ACC1A1
证明:
因为四边形ABCD是菱形,所以BD⊥AC,
*
小结:证明线面垂直的方法关键是证明
线线垂直(三线合一,正方形/菱形对角线,直线与平面垂直,勾股逆定理,直径所对圆周角等)
*
分析:
(菱形的对角线垂直)
高考真题——真枪实战·挑战自我
1.(2014全国Ⅰ文改编) 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.证明:B1C⊥平面ABO;
(直线与平面垂直)
*
高考真题——真枪实战·挑战自我
2.(2018年全国卷I改编)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把ΔDFC折起,使C点到达P点的位置,且PF⊥BF.证明:BF⊥平面PEF;
分析:
(正方形邻边垂直)
20
高考真题——真枪实战·挑战自我
3.(2018年全国卷II)如图,在三棱锥中P—ABC中,AB=BC= ,PA=PB=PC=AC=4,O为AC的中点.证明:PO⊥平面ABC;
分析:
(勾股逆定理)
(三线合一)
*
分析:
(勾股逆定理)
课后巩固——知识预测·总结提升
(直线与平面垂直)
*
2.如图所示,已知PA垂直于⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,求证:BC⊥平面PAC.
课后巩固——知识预测·总结提升
分析:
(直径所对圆周角)
(直线与平面垂直)
*
分析:
图1
图2
课后巩固——知识预测·总结提升
*
本课小结:
这节课你收获了什么知识?
一个定义:
如果直线l与平面α内的任意一条直线都垂直,
我们就说直线l与平面α互相垂直.
一个定理:
一条直线与一个平面内的两条相交直线都垂直,
则该直线与此平面垂直
证明线面垂直的方法关键是证明线线垂直(三线合一,正方形/菱形对角线,直线与平面垂直,勾股逆定理,直径所对圆周角等)
*
*
学习目标:
1.理解直线与平面垂直的定义;
2.掌握直线与平面垂直的判定定理及应用;
3.应用直线与平面垂直的判定定理解决问题;
重点:操作确认并概括出直线与平面垂直的定义和判定定理.
难点:操作确认并概括出直线与平面垂直的判定定理及初步运用.
*
说说它们的位置关系
旗杆与地面:
宿舍楼前的柱子与地面:
桥墩与水面:
垂直
*
l
α
垂直
*
l
α
垂直
尝试概括直线与平面垂直的概念
*
直线与平面垂直的定义:
如果直线l与平面α内的任意一条直线都垂直,我们就说直线l与平面α互相垂直,记作
平面α的垂线
直线l的垂面
垂足
思考:
如何判定一条直线与一个平面是否垂直?
*
探究实验
过顶点 A 随意翻折三角形纸片得到折痕 AD ,将翻折后的纸片竖起放置在桌面上(要求 BD 、DC 与桌面接触),折痕 AD 与桌面垂直吗?如何翻折才能使得 AD 与桌面垂直?
(1)折痕AD与桌面垂直吗?
(2)如何翻折才能使折痕AD与桌面所在平面α垂直?
当且仅当折痕AD是BC边上的高时,AD所在直线与桌面所在平面α垂直
*
再尝试用下列两种形状的纸片,过点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD,DC与桌面接触)
如何翻折才能使折痕AD与桌面所在平面α垂直?
*
当且仅当折痕AD垂直于BC时,AD所在直线与桌面所在平面α垂直
由以上几个折纸试验,不难看出,AD⊥BC时,翻折后垂直关系不变,即AD⊥CD,AD⊥BD,又CD、BD相交于点D,都在桌面所在的平面
猜想得到确认:一条直线和一个平面内两条相交直线都垂直时,该直线与这个平面垂直
*
直线与平面垂直的判定定理:
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直
符号表示:
P
*
预习自测:
1.判断下列说法正确的是:
①若 l⊥α,a?α,则 l⊥a;
②若 a⊥l,a//b,则 b⊥l;
③若直线 l 垂直于平面α内的无数条直线,则 l⊥α;
④若直线 l 垂直于平面α,则 l 与α内的直线可相交,可异面,可平行
①②
*
预习自测:
2.在正方体 ABCD-A1B1C1D1中,
与平面 ABCD 垂直的直线
有____________
与直线 A1A 垂直的平面
有____________
与直线 A1A 垂直的直线
有____________
AA1,BB1,CC1,DD1
平面ABCD,平面A1B1C1D1
AB,BC,CD,DA,A1B1,B1C1,C1D1,D1A1
*
探究案
例题 1 如图,在三棱锥V-ABC中,VA=VC,AB=BC,O为AC的中点,求证:AC⊥平面VOB.
书写过程要求:
①字迹工整清晰;
②每一步骤的依据要表达清楚;
③推出直线与平面垂直的条件缺一不可.
*
探究案
例题 1 如图,在三棱锥V-ABC中,VA=VC,AB=BC,O为AC的中点,求证:AC⊥平面VOB.
*
探究案:
例2.正方体ABCD-A1B1C1D1 中,
求证: BD⊥平面ACC1A1
书写过程要求:
①字迹工整清晰;
②每一步骤的依据要表达清楚;
③推出直线与平面垂直的条件缺一不可.
*
定理应用:
例2.正方体ABCD-A1B1C1D1 中,
求证: BD⊥平面ACC1A1
证明:
因为四边形ABCD是正方形,所以BD⊥AC,
*
变式:在底面为菱形的直棱柱
ABCD-A1B1C1D1 中,
求证: BD⊥平面ACC1A1
证明:
因为四边形ABCD是菱形,所以BD⊥AC,
*
小结:证明线面垂直的方法关键是证明
线线垂直(三线合一,正方形/菱形对角线,直线与平面垂直,勾股逆定理,直径所对圆周角等)
*
分析:
(菱形的对角线垂直)
高考真题——真枪实战·挑战自我
1.(2014全国Ⅰ文改编) 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.证明:B1C⊥平面ABO;
(直线与平面垂直)
*
高考真题——真枪实战·挑战自我
2.(2018年全国卷I改编)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把ΔDFC折起,使C点到达P点的位置,且PF⊥BF.证明:BF⊥平面PEF;
分析:
(正方形邻边垂直)
20
高考真题——真枪实战·挑战自我
3.(2018年全国卷II)如图,在三棱锥中P—ABC中,AB=BC= ,PA=PB=PC=AC=4,O为AC的中点.证明:PO⊥平面ABC;
分析:
(勾股逆定理)
(三线合一)
*
分析:
(勾股逆定理)
课后巩固——知识预测·总结提升
(直线与平面垂直)
*
2.如图所示,已知PA垂直于⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,求证:BC⊥平面PAC.
课后巩固——知识预测·总结提升
分析:
(直径所对圆周角)
(直线与平面垂直)
*
分析:
图1
图2
课后巩固——知识预测·总结提升
*
本课小结:
这节课你收获了什么知识?
一个定义:
如果直线l与平面α内的任意一条直线都垂直,
我们就说直线l与平面α互相垂直.
一个定理:
一条直线与一个平面内的两条相交直线都垂直,
则该直线与此平面垂直
证明线面垂直的方法关键是证明线线垂直(三线合一,正方形/菱形对角线,直线与平面垂直,勾股逆定理,直径所对圆周角等)
*
