2.2.2-平面和平面平行的判定(34张PPT)
文档属性
| 名称 | 2.2.2-平面和平面平行的判定(34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 644.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 00:00:00 | ||
图片预览









文档简介
(共34张PPT)
新课导入
我们已经学过直线与平面平行的判定:
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
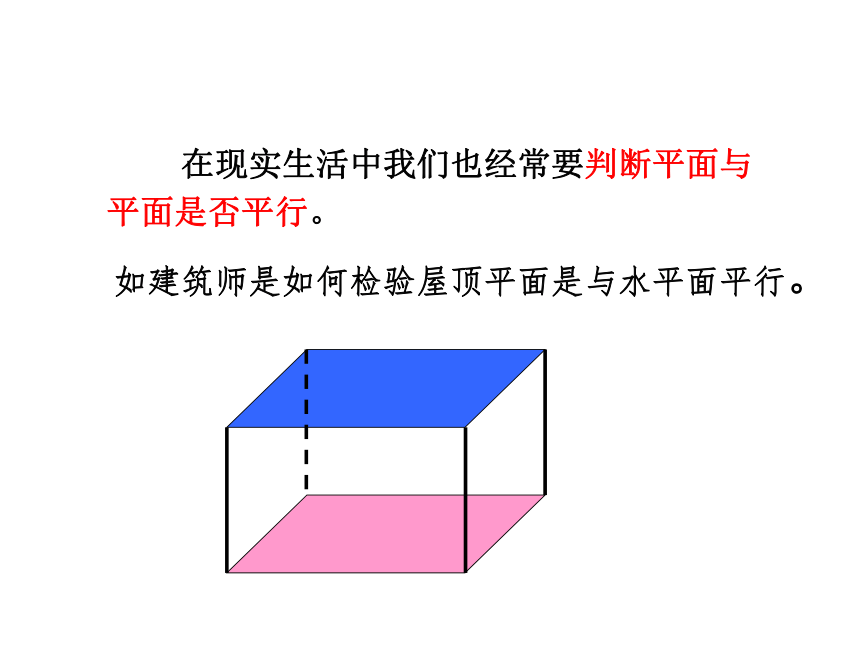
在现实生活中我们也经常要判断平面与平面是否平行。
如建筑师是如何检验屋顶平面是与水平面平行。
国旗下的演讲稿:我的中国梦国梦
国旗下的讲话稿:我的国梦
“我们都有一个家,名字叫国”正如《龙的传人》歌词讲的,我们是华夏族,我们的祖先世世代代都生活在这片华夏土地上——国。每人都有一个富强国的理想,现在,我就说说我的吧。
如今,钓鱼岛事态严重化,虽然国现在很强大,但我认为,国的国防实力还需加强,所以我想成为一名飞行员,守护我们祖国的这片蓝天。
要想成为一名飞行员,就得从细节做起,从一点一滴的小事做起。首先,我应保持一个良好的视力,其次,学习成绩应当优秀,拥有一个良好的视力是我这个梦想的基础,也是关键,因为我要是没有一个良好的视力,学习再好,实现这个愿望也是无稽之谈,其次,若是学习不好,视力好也没有用,没文化,就是个睁眼瞎,所以,两者缺一不可。
我认为以上都不是过于的重要,最最重要的是,人要有个好的思想品德,也就是拥有做人的道德标准,华民族有着五千年的文明历史,我要吸收精华,去其糟粕,提高自己的文化修养和道德标准,为自己插上腾飞的翅膀,才能够实现我们的国梦。
说起国梦,我还有一个,就是从事医学,而且还要当一名军医,虽然军医不能到前线打仗,但在所有的战争军医往往也是非常重要的角色,因为如
是否可以将平面与平面之间的平行判定这个空间问题也转化为平面问题呢?
是否可以将平面与平面之间的平行判定这个空间问题也转化为平面问题呢?
2.2.2 平面与平面平行的判定
教学目标
理解并掌握两平面平行的判定定理。
让学生通过观察实物及模型,得出两平面平行的判定。
进一步培养学生空间问题平面化的思想。
教学重难点
两个平面平行的判定。
判定定理、例题的证明。
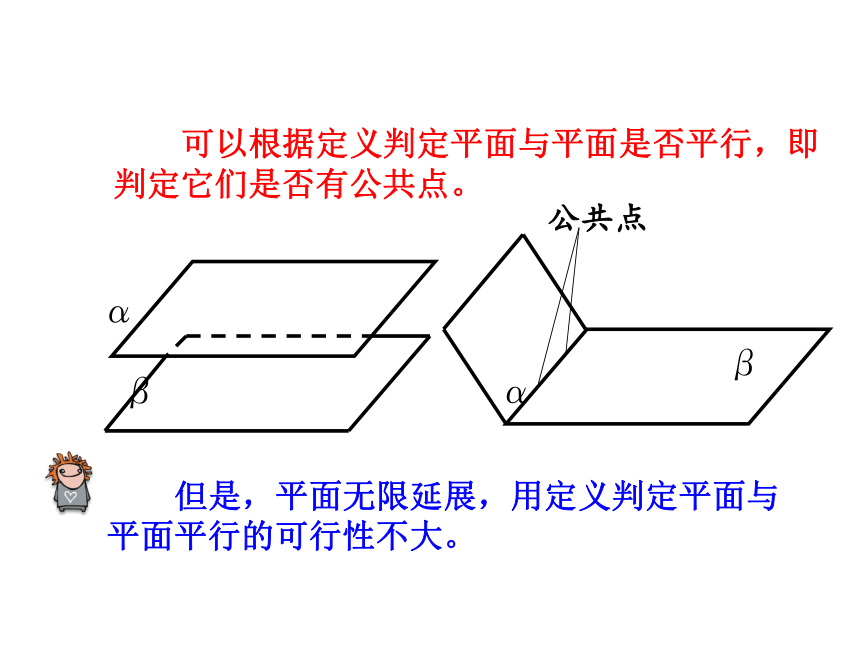
可以根据定义判定平面与平面是否平行,即判定它们是否有公共点。
但是,平面无限延展,用定义判定平面与平面平行的可行性不大。
若一个平面内所有直线都与另一平面平行,那么这两个平面一定不可能相交,所以两面平行。只要有一条直线与另一面相交,则两面不平行。
但是,依然要判断一个平面内所有直线都与另一平面平行,这是很难操作的,能不能根据某几条直线的平行与面平行来判定面面平行呢?
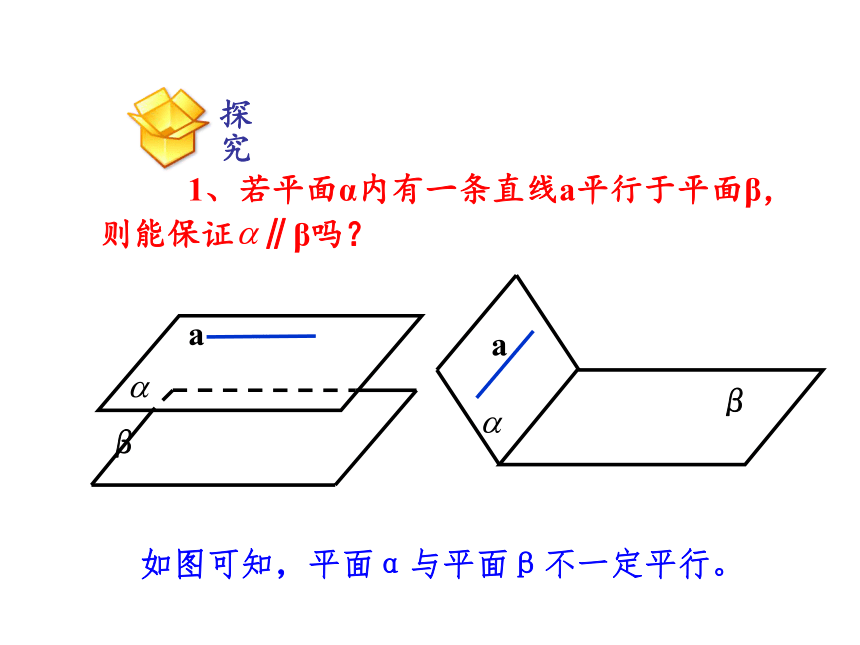
1、若平面α内有一条直线a平行于平面β,则能保证 ∥β吗?
如图可知,平面α与平面β不一定平行。
2、若平面 内有两条直线a、b都平行于平面β,能保证 ∥β吗?
左图中,平面 内两直线平行,两平面不平行。
右图中,平面 内两直线相交,两平面平行。
平面和平面平行的判定定理:
一个平面内有两条相交直线与此另一平面平行,则这两个平面平行。
符号表示:
定理证明
证明:假设α∩β=c.则c∈α,c∈β
∵a∥β, a α,a与c没有交点
∴a∥c.同理b∥c。
于是在平面内过点P有两条直线与c平行,这与平行公理矛盾,假设不成立。
∴ α∥β。
a
α
β
c
b
求证:α∥β
面面问题
线面问题
转化为
转化为
线线问题
解决问题的数学思想:
(1)平行于同一条直线的两平面平行。
错误
(2)若平面α内有两条直线都平行于平面β,则α∥β。
错误
(3)若平面α内有无数条直线都平行于平面β,则α∥β。
错误
(4)过平面外一点,只可作1个平面与已知平行。
正确
(5)设a、b为异面直线,则存在平面α、β,使
正确
分析:
在四边形ABC1D1中,AB∥C1D1且AB=C1D1故四边形ABC1D1为平行四边形。
即AD1∥BC1
证明:
∵ABCD-A1B1C1D1是正方体,
∴D1C1//A1B1,D1C1=A1B1,
AB//A1B1,AB=A1B1,
∴D1C1//AB,D1C1=AB,
∴D1C1BA为平行四边形,
∴ D1A//C1B,
又D1A 平面C1BD,
C1B 平面C1BD,
∴D1A//平面C1BD。
同理D1B1//平面C1BD,
又D1A D1B1=D1,
D1A 平面AB1D1 ,
D1B1 平面AB1D1,
∴平面AB1D1//平面C1BD。
已知正方体ABCD-A1B1C1D1,P、Q、R分别为A1A、AB、AD的中点 .求证:平面PQR∥平面CB1D1。
连结A1B,BD。
因为PQ∥ A1B且A1B ∥CD1。
故PQ∥CD1。
同理可得,RQ//B1D1。
所以平面PQR∥平面CB1D1。
正方体中面与面的平行关系有还有这些:
课堂小结
证明平面与平面平行的方法:
(1)利用定义:
(2)利用判定定理:
平面与平面没有公共点
一个平面内有两条相交直线与此另一平面平行,则这两个平面平行。
平面和平面平行的判定定理:
利用判定定理证明两个平面平行,必须具备以下的两个条件:
(1)有两条直线平行于同一个平面。 (2)这两条直线必须相交。
高考链接
B
【解析】考察直线与平面平行,两平面平行的判定
随堂练习
C
C
1.经过平面外两点可作该平面的平行平面的个数为 ( )
A. 0 B. 1
C. 0或1 D. 1或2
3.下面两组平面哪一组看上去象平行平面?
(1)
(2)
α
β
α
β
1)如果一个平面内的一条直线于行于另一个平面,那么这两个平面平行。
×
2)如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行。
×
3)如果一个平面内的无数条直线平行于另一个平面,那么这两个平面平行。
×
4)如果一个平面内的任何一条直线都平行于另一个平面,那么这两个平面平行。
√
4.判断.
5.求证:垂直于同一条直线的两个平面平行。
已知:α⊥AA',β⊥AA'
求证:α∥β
A
A’
α
β
6.求证:平行于同一个平面的两个平面平行。
已知:α∥γ,β∥γ
求证:α∥β
构造:两个相交的平面M和N平面,分别与α、β、γ平面相交与a、c、e和b、d、f
α
β
γ
习题答案
1.(1)命题不正确。
(2)命题正确。
2.提示:容易证明MN//EF,NA//EB,进而可证平面AMN//平面EFDB。
3.D。
新课导入
我们已经学过直线与平面平行的判定:
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
在现实生活中我们也经常要判断平面与平面是否平行。
如建筑师是如何检验屋顶平面是与水平面平行。
国旗下的演讲稿:我的中国梦国梦
国旗下的讲话稿:我的国梦
“我们都有一个家,名字叫国”正如《龙的传人》歌词讲的,我们是华夏族,我们的祖先世世代代都生活在这片华夏土地上——国。每人都有一个富强国的理想,现在,我就说说我的吧。
如今,钓鱼岛事态严重化,虽然国现在很强大,但我认为,国的国防实力还需加强,所以我想成为一名飞行员,守护我们祖国的这片蓝天。
要想成为一名飞行员,就得从细节做起,从一点一滴的小事做起。首先,我应保持一个良好的视力,其次,学习成绩应当优秀,拥有一个良好的视力是我这个梦想的基础,也是关键,因为我要是没有一个良好的视力,学习再好,实现这个愿望也是无稽之谈,其次,若是学习不好,视力好也没有用,没文化,就是个睁眼瞎,所以,两者缺一不可。
我认为以上都不是过于的重要,最最重要的是,人要有个好的思想品德,也就是拥有做人的道德标准,华民族有着五千年的文明历史,我要吸收精华,去其糟粕,提高自己的文化修养和道德标准,为自己插上腾飞的翅膀,才能够实现我们的国梦。
说起国梦,我还有一个,就是从事医学,而且还要当一名军医,虽然军医不能到前线打仗,但在所有的战争军医往往也是非常重要的角色,因为如
是否可以将平面与平面之间的平行判定这个空间问题也转化为平面问题呢?
是否可以将平面与平面之间的平行判定这个空间问题也转化为平面问题呢?
2.2.2 平面与平面平行的判定
教学目标
理解并掌握两平面平行的判定定理。
让学生通过观察实物及模型,得出两平面平行的判定。
进一步培养学生空间问题平面化的思想。
教学重难点
两个平面平行的判定。
判定定理、例题的证明。
可以根据定义判定平面与平面是否平行,即判定它们是否有公共点。
但是,平面无限延展,用定义判定平面与平面平行的可行性不大。
若一个平面内所有直线都与另一平面平行,那么这两个平面一定不可能相交,所以两面平行。只要有一条直线与另一面相交,则两面不平行。
但是,依然要判断一个平面内所有直线都与另一平面平行,这是很难操作的,能不能根据某几条直线的平行与面平行来判定面面平行呢?
1、若平面α内有一条直线a平行于平面β,则能保证 ∥β吗?
如图可知,平面α与平面β不一定平行。
2、若平面 内有两条直线a、b都平行于平面β,能保证 ∥β吗?
左图中,平面 内两直线平行,两平面不平行。
右图中,平面 内两直线相交,两平面平行。
平面和平面平行的判定定理:
一个平面内有两条相交直线与此另一平面平行,则这两个平面平行。
符号表示:
定理证明
证明:假设α∩β=c.则c∈α,c∈β
∵a∥β, a α,a与c没有交点
∴a∥c.同理b∥c。
于是在平面内过点P有两条直线与c平行,这与平行公理矛盾,假设不成立。
∴ α∥β。
a
α
β
c
b
求证:α∥β
面面问题
线面问题
转化为
转化为
线线问题
解决问题的数学思想:
(1)平行于同一条直线的两平面平行。
错误
(2)若平面α内有两条直线都平行于平面β,则α∥β。
错误
(3)若平面α内有无数条直线都平行于平面β,则α∥β。
错误
(4)过平面外一点,只可作1个平面与已知平行。
正确
(5)设a、b为异面直线,则存在平面α、β,使
正确
分析:
在四边形ABC1D1中,AB∥C1D1且AB=C1D1故四边形ABC1D1为平行四边形。
即AD1∥BC1
证明:
∵ABCD-A1B1C1D1是正方体,
∴D1C1//A1B1,D1C1=A1B1,
AB//A1B1,AB=A1B1,
∴D1C1//AB,D1C1=AB,
∴D1C1BA为平行四边形,
∴ D1A//C1B,
又D1A 平面C1BD,
C1B 平面C1BD,
∴D1A//平面C1BD。
同理D1B1//平面C1BD,
又D1A D1B1=D1,
D1A 平面AB1D1 ,
D1B1 平面AB1D1,
∴平面AB1D1//平面C1BD。
已知正方体ABCD-A1B1C1D1,P、Q、R分别为A1A、AB、AD的中点 .求证:平面PQR∥平面CB1D1。
连结A1B,BD。
因为PQ∥ A1B且A1B ∥CD1。
故PQ∥CD1。
同理可得,RQ//B1D1。
所以平面PQR∥平面CB1D1。
正方体中面与面的平行关系有还有这些:
课堂小结
证明平面与平面平行的方法:
(1)利用定义:
(2)利用判定定理:
平面与平面没有公共点
一个平面内有两条相交直线与此另一平面平行,则这两个平面平行。
平面和平面平行的判定定理:
利用判定定理证明两个平面平行,必须具备以下的两个条件:
(1)有两条直线平行于同一个平面。 (2)这两条直线必须相交。
高考链接
B
【解析】考察直线与平面平行,两平面平行的判定
随堂练习
C
C
1.经过平面外两点可作该平面的平行平面的个数为 ( )
A. 0 B. 1
C. 0或1 D. 1或2
3.下面两组平面哪一组看上去象平行平面?
(1)
(2)
α
β
α
β
1)如果一个平面内的一条直线于行于另一个平面,那么这两个平面平行。
×
2)如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行。
×
3)如果一个平面内的无数条直线平行于另一个平面,那么这两个平面平行。
×
4)如果一个平面内的任何一条直线都平行于另一个平面,那么这两个平面平行。
√
4.判断.
5.求证:垂直于同一条直线的两个平面平行。
已知:α⊥AA',β⊥AA'
求证:α∥β
A
A’
α
β
6.求证:平行于同一个平面的两个平面平行。
已知:α∥γ,β∥γ
求证:α∥β
构造:两个相交的平面M和N平面,分别与α、β、γ平面相交与a、c、e和b、d、f
α
β
γ
习题答案
1.(1)命题不正确。
(2)命题正确。
2.提示:容易证明MN//EF,NA//EB,进而可证平面AMN//平面EFDB。
3.D。
