北师大版七年级数学下册3.2 用关系式表示的变量间关系课件(共18张PPT)
文档属性
| 名称 | 北师大版七年级数学下册3.2 用关系式表示的变量间关系课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 659.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 12:40:56 | ||
图片预览





文档简介
(共18张PPT)
用关系式表示的变量间关系
学习目标:
能根据具体情景,用关系式表示某些变 量之间的关系。
能根据关系式求值,初步体会自变量和 因变量的数值对应关系。
一、情景引入:
请同学们观察表格,已知三角形的底边长为8cm时,三角形的面积y(cm2)与三角形的高h(cm)有如下的关系:
三角形的高h 1 2 3 4 5 6 7
三角形的面积y 4 8 12 16 20 24 28
(1)表格反映的是哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)通过表格,你发现了什么规律?如何表示呢?
D
B
C
A
思考:确定一个三角形的面积需要哪些量呢?
二、新知讲授:
三角形ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生变化么?
(1)平面图形的探讨:
A
B
C
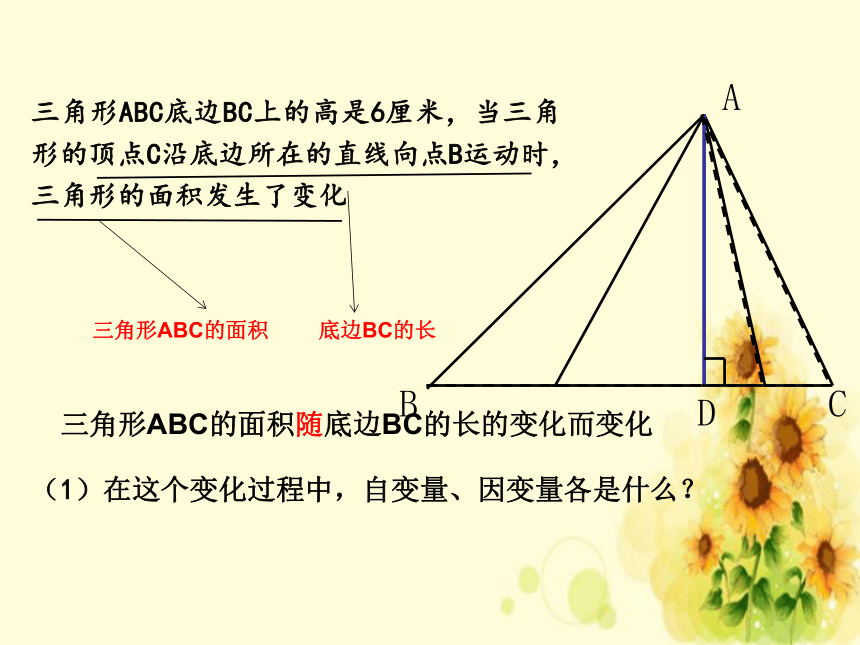
三角形ABC底边BC上的高是6厘米,当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了变化
底边BC的长
三角形ABC的面积
三角形ABC的面积随底边BC的长的变化而变化
(1)在这个变化过程中,自变量、因变量各是什么?
D
三角形ABC底边BC上的高是6厘米,当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了怎样的变化?
(2)如果三角形的底边长为x(cm),那么三角形的面积y(cm2)可以表示为________。
(3)当底边长从12cm变化到3cm时,三角形的面积从____cm2变化到___cm2
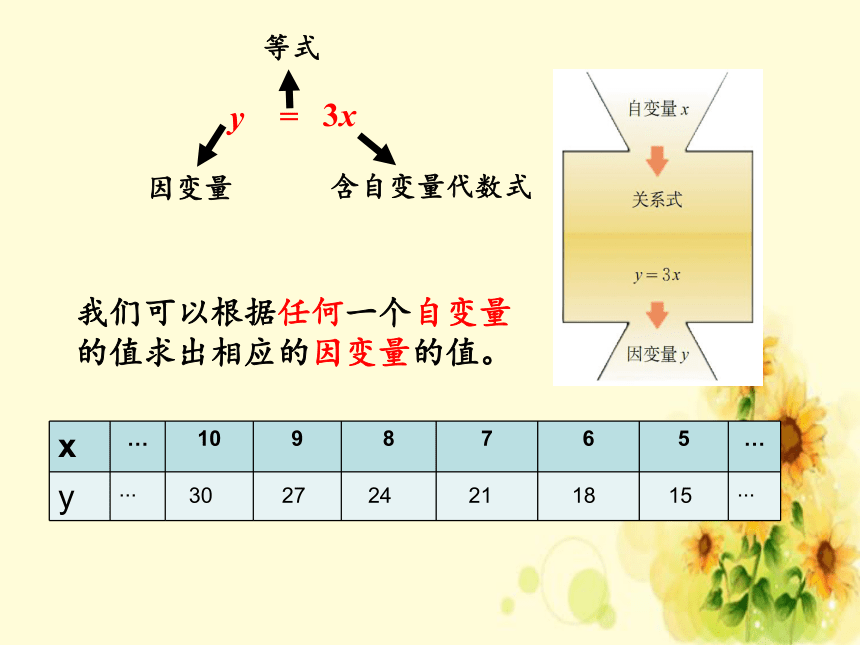
y=3x
36
9
y=3x表示了 和 之间的关系,它是变量 随 变化而变化的关系式。
三角形底边长 x
面积 y
y
x
x … 10 9 8 7 6 5 …
y ... ...
我们可以根据任何一个自变量的值求出相应的因变量的值。
30
18
15
27
24
21
3x
=
y
因变量
含自变量代数式
等式
我们还学过许多的平面几何图形,比如:长方形、梯形、圆等等,你们能参照上面的方法对这些平面几何图形中的相关数量关系进行探究么?请大家分组合作探究,然后展示你们的结果。
小组合作,深入探究
例:如图,设三角形的高为6cm,底边BC长为x(cm),三角形的面积y(cm2),根据三角形的面积公式,得到关系式:y=3x
D
B
C
A
(2)如果圆锥底面半径为r(厘米),那么
圆锥的体积V(厘米3)与r的关系式为___
如图,圆锥的高度是4厘米,当圆锥的的底面半径由小到大变化时,圆锥的体积也随之发生了变化。
4厘米
(1)在这个变化过程中,自变量、因变量各是什么?
(3)当底面半径由1厘米变化到10厘米时,
圆锥的体积由 厘米3变化到 厘米3 。
(2)立体图形的探讨:
你知道什么是“低碳生活吗”?“低碳生活”是指人们生活中尽量减少所耗能量,从而降低(特别是二氧化碳)的排放量的一种生活方式。
(3)运用迁移:
1、用字母表示家居用电的二氧化碳排放量的关系式为________,其中字母表示__________。
y=0.785x
y表示二氧化碳排放量,x表示耗电量
(2)在上述关系式中,耗电量每增加1 KW·h,二氧化碳排放量增加___________。当耗电量从1 KW·h增加到100KW·h时,二氧化碳排放量从_______增加到_____________。
0.785kg
0.785kg
78.5kg
你能说一说家用自来水二氧化碳排放量随自来水使用吨数的变化而变化的情况吗?
(3)小明家本月用电大约110 KW·h、天然气20m3、自来水5t、油耗75L,请你计算一下小明家这几项的二氧化碳排放量。
297.2kg
1、变量m、n之间的关系式是m=2n-1,当自变量n=2时,因变量m的值是( )
A、2 B、3
C、-3 D、5
2.张老师带领 x 名学生到某动物园参观,已知成人票每张10元,学生票每张5元,设门票的总费用为y元,则 y = .
三、反馈练习:
5x+10
B
3、某弹簧的自然长度为3cm,在弹性限度内所挂的物体的重量x 每增加1 kg ,弹簧长度y增加0.5cm。
x/kg 1 2 3 4 5 ……
y/cm ……
(1)依据上表数据,写出y与x之间的关系式。
3.5
4
4.5
5
5.5
(2)当物体的质量为6kg时,根据(1)的关 系式求出弹簧的长度。
y = 3+0.5x
【解析】将x=6代入y=3+0.5*6,得y=3+3=6.
四、课堂小结:
1、总结知识:本节课你学到了什么?
2、你认为在今后的练习过程中,大家需要注意什么呢?
1、习题3.2第一二题写在书上
2、习题3.2第三题写在作业本上
3、思考:还有什么方法更能直观地表示变量之间的关系么?
五、作业布置:
再见
用关系式表示的变量间关系
学习目标:
能根据具体情景,用关系式表示某些变 量之间的关系。
能根据关系式求值,初步体会自变量和 因变量的数值对应关系。
一、情景引入:
请同学们观察表格,已知三角形的底边长为8cm时,三角形的面积y(cm2)与三角形的高h(cm)有如下的关系:
三角形的高h 1 2 3 4 5 6 7
三角形的面积y 4 8 12 16 20 24 28
(1)表格反映的是哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)通过表格,你发现了什么规律?如何表示呢?
D
B
C
A
思考:确定一个三角形的面积需要哪些量呢?
二、新知讲授:
三角形ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生变化么?
(1)平面图形的探讨:
A
B
C
三角形ABC底边BC上的高是6厘米,当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了变化
底边BC的长
三角形ABC的面积
三角形ABC的面积随底边BC的长的变化而变化
(1)在这个变化过程中,自变量、因变量各是什么?
D
三角形ABC底边BC上的高是6厘米,当三角形的顶点C沿底边所在的直线向点B运动时,三角形的面积发生了怎样的变化?
(2)如果三角形的底边长为x(cm),那么三角形的面积y(cm2)可以表示为________。
(3)当底边长从12cm变化到3cm时,三角形的面积从____cm2变化到___cm2
y=3x
36
9
y=3x表示了 和 之间的关系,它是变量 随 变化而变化的关系式。
三角形底边长 x
面积 y
y
x
x … 10 9 8 7 6 5 …
y ... ...
我们可以根据任何一个自变量的值求出相应的因变量的值。
30
18
15
27
24
21
3x
=
y
因变量
含自变量代数式
等式
我们还学过许多的平面几何图形,比如:长方形、梯形、圆等等,你们能参照上面的方法对这些平面几何图形中的相关数量关系进行探究么?请大家分组合作探究,然后展示你们的结果。
小组合作,深入探究
例:如图,设三角形的高为6cm,底边BC长为x(cm),三角形的面积y(cm2),根据三角形的面积公式,得到关系式:y=3x
D
B
C
A
(2)如果圆锥底面半径为r(厘米),那么
圆锥的体积V(厘米3)与r的关系式为___
如图,圆锥的高度是4厘米,当圆锥的的底面半径由小到大变化时,圆锥的体积也随之发生了变化。
4厘米
(1)在这个变化过程中,自变量、因变量各是什么?
(3)当底面半径由1厘米变化到10厘米时,
圆锥的体积由 厘米3变化到 厘米3 。
(2)立体图形的探讨:
你知道什么是“低碳生活吗”?“低碳生活”是指人们生活中尽量减少所耗能量,从而降低(特别是二氧化碳)的排放量的一种生活方式。
(3)运用迁移:
1、用字母表示家居用电的二氧化碳排放量的关系式为________,其中字母表示__________。
y=0.785x
y表示二氧化碳排放量,x表示耗电量
(2)在上述关系式中,耗电量每增加1 KW·h,二氧化碳排放量增加___________。当耗电量从1 KW·h增加到100KW·h时,二氧化碳排放量从_______增加到_____________。
0.785kg
0.785kg
78.5kg
你能说一说家用自来水二氧化碳排放量随自来水使用吨数的变化而变化的情况吗?
(3)小明家本月用电大约110 KW·h、天然气20m3、自来水5t、油耗75L,请你计算一下小明家这几项的二氧化碳排放量。
297.2kg
1、变量m、n之间的关系式是m=2n-1,当自变量n=2时,因变量m的值是( )
A、2 B、3
C、-3 D、5
2.张老师带领 x 名学生到某动物园参观,已知成人票每张10元,学生票每张5元,设门票的总费用为y元,则 y = .
三、反馈练习:
5x+10
B
3、某弹簧的自然长度为3cm,在弹性限度内所挂的物体的重量x 每增加1 kg ,弹簧长度y增加0.5cm。
x/kg 1 2 3 4 5 ……
y/cm ……
(1)依据上表数据,写出y与x之间的关系式。
3.5
4
4.5
5
5.5
(2)当物体的质量为6kg时,根据(1)的关 系式求出弹簧的长度。
y = 3+0.5x
【解析】将x=6代入y=3+0.5*6,得y=3+3=6.
四、课堂小结:
1、总结知识:本节课你学到了什么?
2、你认为在今后的练习过程中,大家需要注意什么呢?
1、习题3.2第一二题写在书上
2、习题3.2第三题写在作业本上
3、思考:还有什么方法更能直观地表示变量之间的关系么?
五、作业布置:
再见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
