苏科版八年级数学下册第九章中心对称图形-平行四边形单元测试(含答案)
文档属性
| 名称 | 苏科版八年级数学下册第九章中心对称图形-平行四边形单元测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 274.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 13:21:58 | ||
图片预览

文档简介
苏科版八年级数学下册第九章中心对称图形-平行四边形单元测试
一、单选题
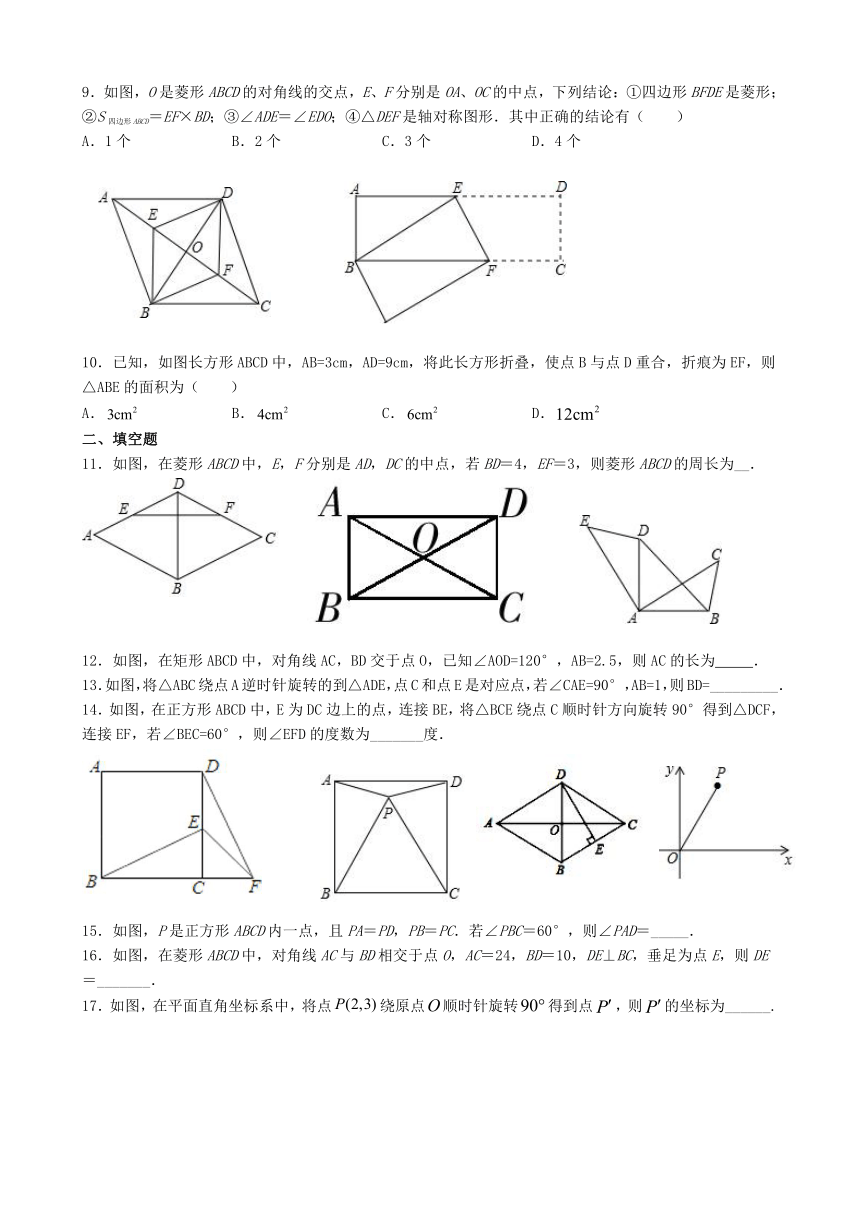
1.下列手机手势解锁图案中,是中心对称图形的是(? ?)
A. B. C. D.
2.在下列命题中,属于真命题的是( )
A.两条对角线相等的四边形是矩形 B.两条对角线互相垂直的四边形是菱形
C.两条对角线互相平分的四边形是平行四边形 D.两条对角线互相垂直且相等的四边形是正方形
3.顺次连结矩形各边的中点所得的四边形是( )
A.正方形 B.菱形 C.矩形 D.平行四边形
4.正方形具有而菱形不一定具有的性质是 ( )
A.对角线相等 B.对角线互相垂直平分
C.四条边相等 D.对角线平分一组对角
5.如图,菱形中,对角线、交于点,为边中点,菱形的周长为28,则的长等于( )
A.3.5 B.4 C.7 D.14
6.如图,在Rt△ABC中,∠BAC=90°.将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C,点A在边B′C上,则∠B′的大小为( )
A.42° B.48° C.52° D.58°
7.如图,△ABC中,D是AB的中点,DE∥BC,连接BE.若AE=6,DE=5,∠BEC=90°,则△BCE的周长是( )
A.12 B.24 C.36 D.48
8.如图,下列条件不能判定四边形ABCD是矩形的是( )
A.∠DAB=∠ABC=∠BCD=90° B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DO D.AO=BO=CO=DO
9.如图,O是菱形ABCD的对角线的交点,E、F分别是OA、OC的中点,下列结论:①四边形BFDE是菱形;②S四边形ABCD=EF×BD;③∠ADE=∠EDO;④△DEF是轴对称图形.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
10.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A. B. C. D.
二、填空题
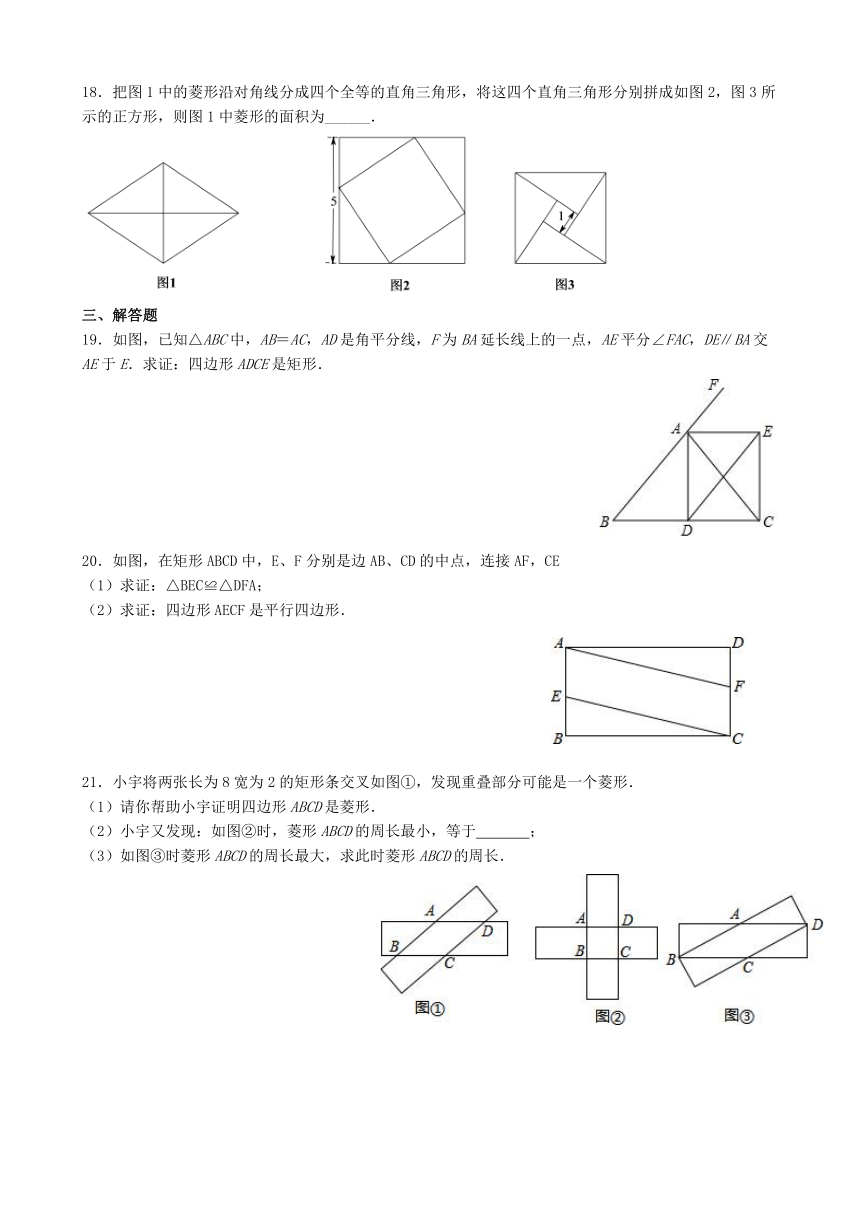
11.如图,在菱形ABCD中,E,F分别是AD,DC的中点,若BD=4,EF=3,则菱形ABCD的周长为__.
12.如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=2.5,则AC的长为 .
13.如图,将△ABC绕点A逆时针旋转的到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD=_________.
14.如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为_______度.
15.如图,P是正方形ABCD内一点,且PA=PD,PB=PC.若∠PBC=60°,则∠PAD=_____.
16.如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=24,BD=10,DE⊥BC,垂足为点E,则DE=_______.
17.如图,在平面直角坐标系中,将点绕原点顺时针旋转得到点,则的坐标为______.
18.把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形,则图1中菱形的面积为______.
三、解答题
19.如图,已知△ABC中,AB=AC,AD是角平分线,F为BA延长线上的一点,AE平分∠FAC,DE∥BA交AE于E.求证:四边形ADCE是矩形.
20.如图,在矩形ABCD中,E、F分别是边AB、CD的中点,连接AF,CE
(1)求证:△BEC≌△DFA;
(2)求证:四边形AECF是平行四边形.
21.小宇将两张长为8宽为2的矩形条交叉如图①,发现重叠部分可能是一个菱形.
(1)请你帮助小宇证明四边形ABCD是菱形.
(2)小宇又发现:如图②时,菱形ABCD的周长最小,等于 ;
(3)如图③时菱形ABCD的周长最大,求此时菱形ABCD的周长.
22.如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A﹣B﹣C﹣D回到点A,设点P运动的时间为t秒.
(1)当t=3秒时,求△ABP的面积;
(2)当t为何值时,点P与点A的距离为5cm?
(3)当t为何值时(2<t<5),以线段AD、CP、AP的长度为三边长的三角形是直角三角形,且AP是斜边.
23.如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE,
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
24.如图,E为正方形ABCD内一点,且EBC是等边三角形,求∠EAD的度数.
25.已知:如图,,,分别是,的中点.
求证:.
26.如图,在平面直角坐标系中,A、B坐标分别为A(0,a)、B(b,a),且a,b满足:(a-3)2+=0,现同时将点A、B分别向下平移3个单位,再向左平移1个单位,分别得到点A、B的对应点C、D,连接AC、BD、AB.
(1)求点C、D的坐标及四边形ABDC的面积S四边形ABDC;
(2)在y轴上是否存在点M,连接MC、MD,使S△MCD=四边形ABDC?若存在这样的点,求出点M的坐标;若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PA、PO,当点P在BD上移动时(不与B、D重合),的值是否发生变化,并说明理由.
参考答案
1.B2.C3.B4.A5.A6.A7.B8.C9.C10.C
11.. 12.5. 13.. 14.15 15.15° 16. 17. 18.12.
19.略
20.(1)证明略,(2)证明略21.(1)略;(2)8;(3)17
22.(1)4;(2)当秒或时,AP=5cm;(3)t=.
23.解:(1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形.
∵AB=AC,AD是△ABC的角平分线,∴AD⊥BC.
∴∠ADB=90°.
∴平行四边形AEBD是矩形.
(2)当∠BAC=90°时,矩形AEBD是正方形.理由如下:
∵∠BAC=90°,AB=AC,AD是△ABC的角平分线,∴AD=BD=CD.
∵由(1)得四边形AEBD是矩形,∴矩形AEBD是正方形.
24.15°
25.略.
26.(1)S四边形ABDC=15;(2)存在点M(0,6)或(0,-6),使S△MCD=S四边形ABDC ,见解析;(3)不变,略.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
