六年级下册数学一课一练-第三单元圆柱与圆锥 (6课时含答案)人教版
文档属性
| 名称 | 六年级下册数学一课一练-第三单元圆柱与圆锥 (6课时含答案)人教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 907.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 00:00:00 | ||
图片预览


文档简介
人教版六年级数学下册第三单元圆柱与圆锥第1节圆柱一课一练测试题
第1课时 圆柱的认识
一、填一填。
1.圆柱是由( )个面围成的。圆柱的上、下两个面叫做( ),它们是相等的两个( ),圆柱周围的面(上、下底面除外)叫做( )。
2.圆柱的两个底面之间的( )叫做圆柱的高,圆柱的高有( )条。
二、请你在圆柱的下面画“○”。
( ) ( ) ( )
( ) ( ) ( )
三、折一折,想一想,能得到什么图形?写在括号里。
( ) ( ) ( )
四、选一选。(将正确答案的序号填在括号里)
1.下图中,图( )中的线段表示的是圆柱的高。
A B C
2.下面各图中,图( )是圆柱的展开图。
A B C
3.如下图,把下面的立体图形切开,图( )切开后的形状是圆。
A B C
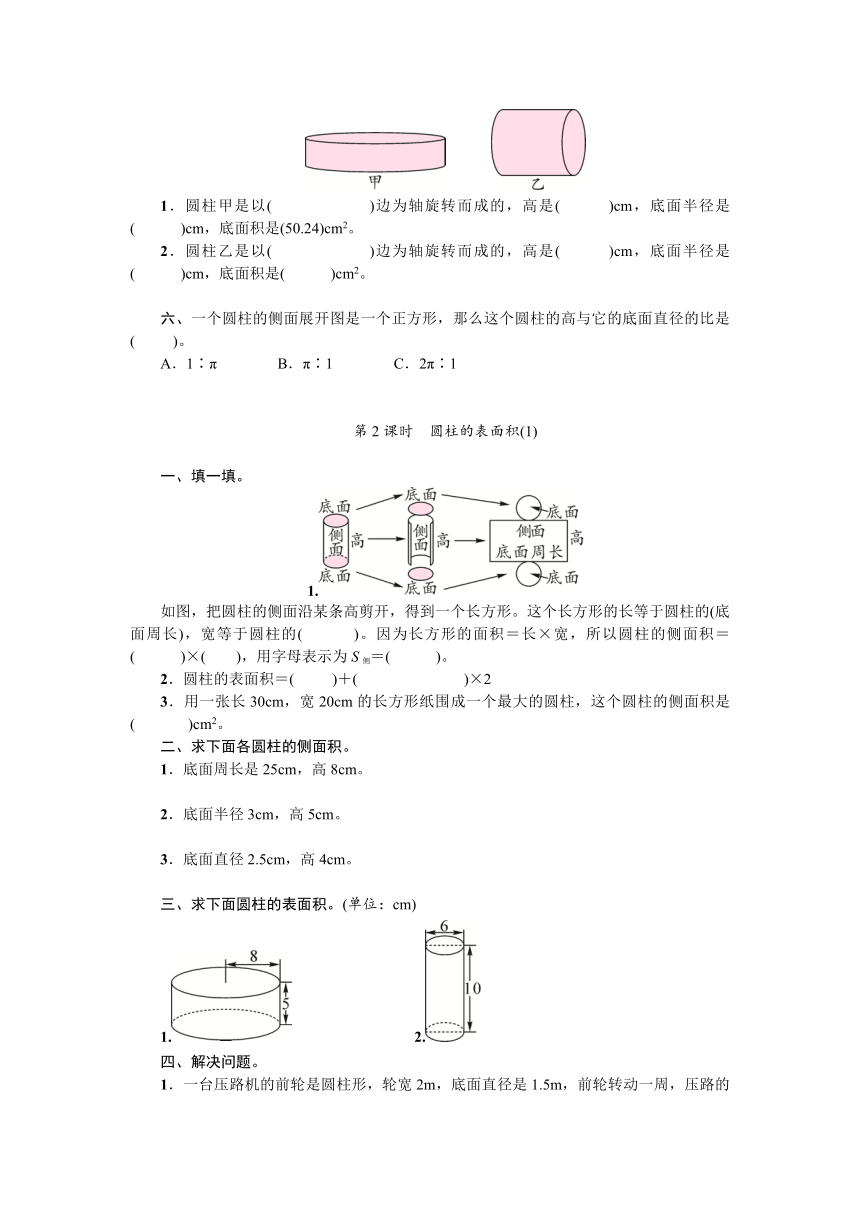
五、分别转动长方形的长和宽形成下面的两个圆柱。(教材P18做一做第2题变式题)
1.圆柱甲是以( )边为轴旋转而成的,高是( )cm,底面半径是( )cm,底面积是(50.24)cm2。
2.圆柱乙是以( )边为轴旋转而成的,高是( )cm,底面半径是( )cm,底面积是( )cm2。
六、一个圆柱的侧面展开图是一个正方形,那么这个圆柱的高与它的底面直径的比是( )。
A.1∶π B.π∶1 C.2π∶1
第2课时 圆柱的表面积(1)
一、填一填。
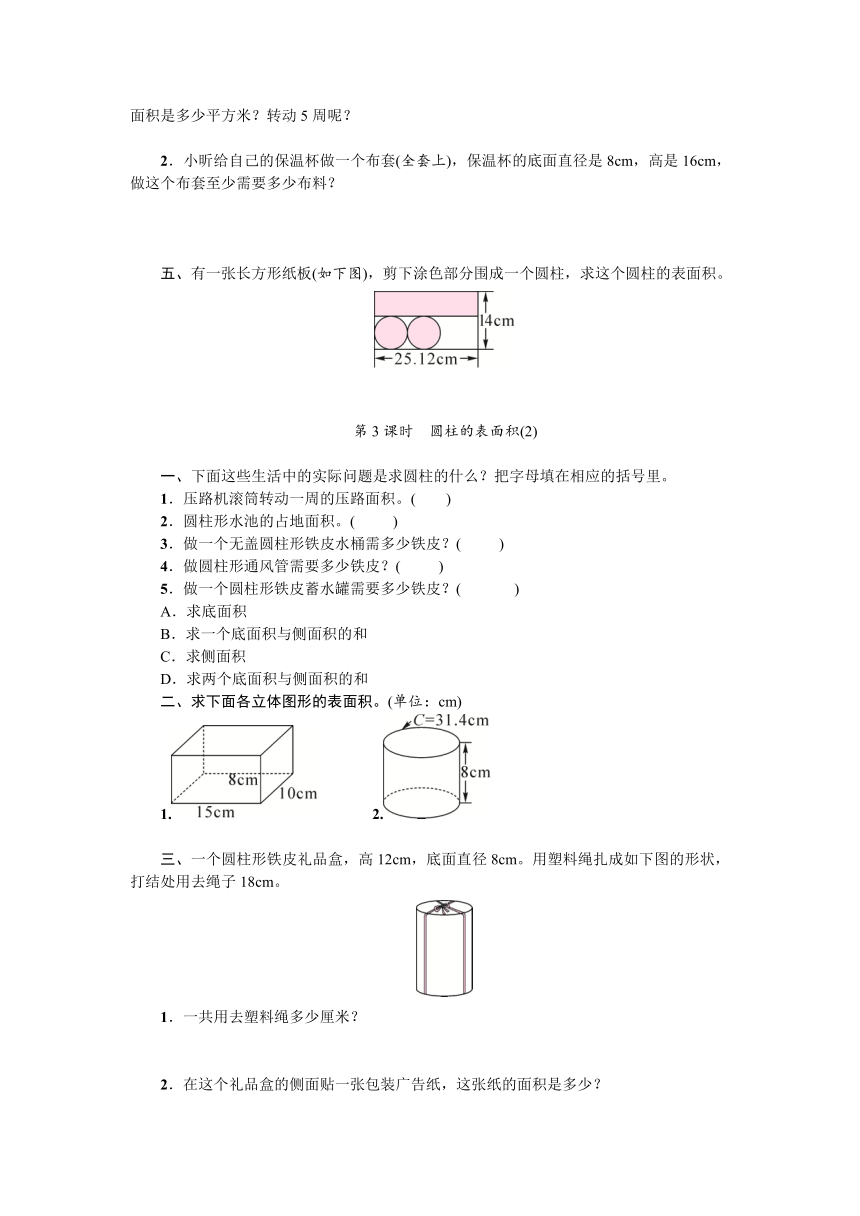
1.
如图,把圆柱的侧面沿某条高剪开,得到一个长方形。这个长方形的长等于圆柱的(底面周长),宽等于圆柱的( )。因为长方形的面积=长×宽,所以圆柱的侧面积=( )×( ),用字母表示为S侧=( )。
2.圆柱的表面积=( )+( )×2
3.用一张长30cm,宽20cm的长方形纸围成一个最大的圆柱,这个圆柱的侧面积是( )cm2。
二、求下面各圆柱的侧面积。
1.底面周长是25cm,高8cm。
2.底面半径3cm,高5cm。
3.底面直径2.5cm,高4cm。
三、求下面圆柱的表面积。(单位:cm)
1. 2.
四、解决问题。
1.一台压路机的前轮是圆柱形,轮宽2m,底面直径是1.5m,前轮转动一周,压路的面积是多少平方米?转动5周呢?
2.小昕给自己的保温杯做一个布套(全套上),保温杯的底面直径是8cm,高是16cm,做这个布套至少需要多少布料?
五、有一张长方形纸板(如下图),剪下涂色部分围成一个圆柱,求这个圆柱的表面积。
第3课时 圆柱的表面积(2)
一、下面这些生活中的实际问题是求圆柱的什么?把字母填在相应的括号里。
1.压路机滚筒转动一周的压路面积。( )
2.圆柱形水池的占地面积。( )
3.做一个无盖圆柱形铁皮水桶需多少铁皮?( )
4.做圆柱形通风管需要多少铁皮?( )
5.做一个圆柱形铁皮蓄水罐需要多少铁皮?( )
A.求底面积
B.求一个底面积与侧面积的和
C.求侧面积
D.求两个底面积与侧面积的和
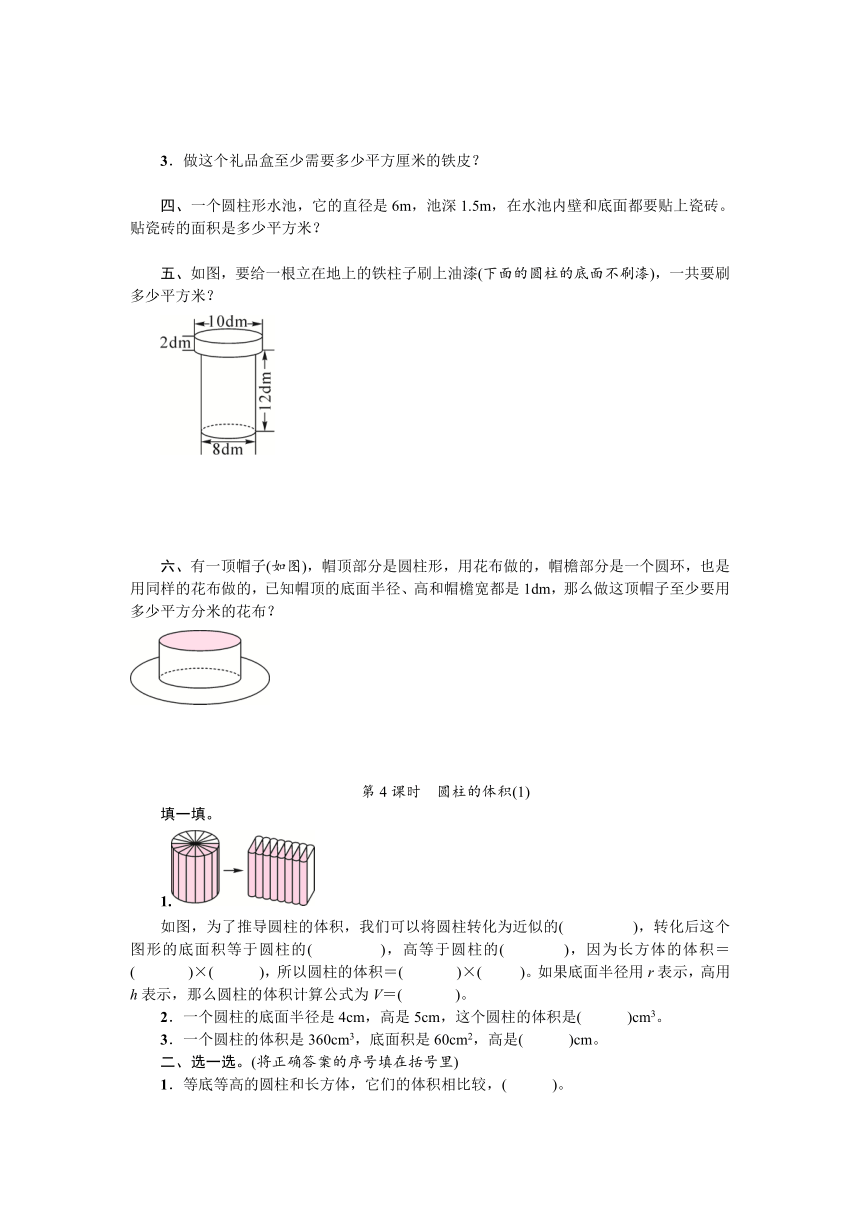
二、求下面各立体图形的表面积。(单位:cm)
1. 2.
三、一个圆柱形铁皮礼品盒,高12cm,底面直径8cm。用塑料绳扎成如下图的形状,打结处用去绳子18cm。
1.一共用去塑料绳多少厘米?
2.在这个礼品盒的侧面贴一张包装广告纸,这张纸的面积是多少?
3.做这个礼品盒至少需要多少平方厘米的铁皮?
四、一个圆柱形水池,它的直径是6m,池深1.5m,在水池内壁和底面都要贴上瓷砖。贴瓷砖的面积是多少平方米?
五、如图,要给一根立在地上的铁柱子刷上油漆(下面的圆柱的底面不刷漆),一共要刷多少平方米?
六、有一顶帽子(如图),帽顶部分是圆柱形,用花布做的,帽檐部分是一个圆环,也是用同样的花布做的,已知帽顶的底面半径、高和帽檐宽都是1dm,那么做这顶帽子至少要用多少平方分米的花布?
第4课时 圆柱的体积(1)
填一填。
1.
如图,为了推导圆柱的体积,我们可以将圆柱转化为近似的( ),转化后这个图形的底面积等于圆柱的( ),高等于圆柱的( ),因为长方体的体积=( )×( ),所以圆柱的体积=( )×( )。如果底面半径用r表示,高用h表示,那么圆柱的体积计算公式为V=( )。
2.一个圆柱的底面半径是4cm,高是5cm,这个圆柱的体积是( )cm3。
3.一个圆柱的体积是360cm3,底面积是60cm2,高是( )cm。
二、选一选。(将正确答案的序号填在括号里)
1.等底等高的圆柱和长方体,它们的体积相比较,( )。
A.圆柱的体积大 B.长方体的体积大
C.一样大
2.将一个圆柱通过切、拼,转化成一个近似的长方体,在这个过程中,( )。
A.表面积和体积都不变
B.体积不变,表面积变大
C.表面积不变,体积变大
三、求下面圆柱的体积。
1.
2.圆柱的底面积是25cm2,高是4cm。
3.圆柱的底面周长是25.12cm,高是半径的1.5倍。
四、解决问题。
1.一口圆柱形水井,井水深5m,底面直径为2m,现在井内有水多少立方米?
2.一个装满酒的圆柱形酒桶,从里面量,它的底面半径是5dm,高为1m。如果每升酒按20元计算,这桶酒价值多少钱?
五、有一根长1m的圆柱形钢材,把它截成三段后,表面积比原来增加216cm2,这根钢材原来的体积是多少立方厘米?
六、把一个高是10cm的圆柱按下图切开,拼成近似的长方体,表面积增加了60cm2。圆柱的体积是多少立方厘米?
第5课时 圆柱的体积(2)
一、填一填。
1.做一个圆柱形铁皮罐头盒,求需要多少铁皮,是求罐头盒的(表面积);求罐头盒可以容纳多少物体,是求罐头盒的( )。
2.0.45L=( )cm3 3.9m3=( )L
750cm3=( )mL=( )dm3
3.一个圆柱的侧面积是125.6cm2,高是10cm,它的底面半径是( )cm,体积是( )cm3。
4.一个圆柱的高不变,底面半径扩大到原来的3倍,体积会扩大到原来的( )倍。
二、选一选。(将正确答案的序号填在括号里)
1.两个体积相等的圆柱,它们一定是( )。
A.底面积和高都相等
B.底面积相等,高不相等
C.底面积和高的乘积相等
2.一个圆柱形水桶底面积是15dm2,容积是120L,高是( )dm。
A.8 B.0.8 C.18
3.把一个棱长是4dm的正方体木块削成一个最大的圆柱,这个圆柱的体积是( )dm3。
A.50.24 B.64 C.100.48
三、填表。
四、解决问题。
1.有两个底面积相等的圆柱,一个圆柱的高是12cm,体积是1800cm3,另一个圆柱的高是20cm,它的体积是多少?
1800÷12×20=3000(cm3)
答:它的体积是3000cm3。
2.周末,小明请六位小朋友来家做客,妈妈准备了一盒果汁,正好可以倒满下面这种杯子6杯,如果让每位小朋友、小明和妈妈每人都喝上果汁,平均每人倒多少毫升?
3.一段长2m的圆柱形钢材,底面直径是20cm。如果加工一个汽车零件要用去钢材5cm3。这段钢材能生产多少个这种零件?
2m=200cm
五、如图,一个圆柱的高增加5cm后,圆柱的表面积增加了62.8cm2。求原圆柱的体积是多少立方厘米?
第6课时 圆柱的体积(3)
一、一个瓶子的内直径是8cm,装入10cm高的水后,盖好瓶盖倒过来放平(如图),量得空余部分的高是2.5cm,这个瓶子的容积是多少毫升?
水的体积:
________________________________________________________________________
空余部分的体积:
________________________________________________________________________
________________________________________________________________________
瓶子的容积:
________________________________________________________________________
________________________________________________________________________
答:这个瓶子的容积是( )mL。
二、填一填。
1.一块不规则的石头,放在装有100mL水的量杯内(石头完全浸没在水中),结果量杯中的水面上升到130mL处,这块不规则的石头的体积是( )mL。
2.一根圆柱形水管的内直径是4cm,水管里的水流动速度是每秒20cm,每分钟流过水管的水有( )mL。
三、一瓶装满的酱油,妈妈炒菜用去了一些后酱油高15cm。把瓶盖拧紧后倒置放平,空余部分高10cm,瓶内直径是8cm。妈妈炒菜用了多少酱油?
四、看图计算。
1.下图是一根空心钢管,求空心钢管的体积。(单位:cm)
2.鲜奶倒进杯子里后,奶面离杯口还有几厘米?
五、一个容积为10L的油壶,壶中油深20cm。把油壶盖拧紧倒立放平,这时瓶中空余部分高5cm,壶中装有油多少升?
六、下面三个图形的面积都是24cm2。把这些图形分别卷成圆柱,卷成的圆柱体积最小的是(A),体积最大的是(A)。(单位:cm)
答案
第1课时 圆柱的认识
一、 1.3 底面 圆 侧面 2.距离 无数
二、(○) () (○) () () (○)
三、长方体 圆柱 正方体
四、1.A 2.C 3.B
五、1.AD或BC 2 4 50.24 2.AB或CD 4 2 12.56
六、B
第2课时 圆柱的表面积(1)
一、1.底面周长 高 底面周长 高 Ch2.侧面积 底面积 3.600
二、1.S侧=Ch=25×8=200(cm2)
2.S侧=2πrh=2×3.14×3×5=94.2(cm2)
3.S侧=πdh=3.14×2.5×4=31.4(cm2)
三、1.S表=2πr2+2πrh=2×3.14×82+2×3.14×8×5=653.12(cm2)
2.r=d÷2=6÷2=3(cm)
S表=2πr2+2πrh=2×3.14×32+2×3.14×3×10=244.92(cm2)
四、1.1.5×3.14×2=9.42(m2) 9.42×5=47.1(m2)
2.2×3.14×(8÷2)2+8×3.14×16=502.4(cm2)
五、底面直径:25.12÷3.14=8(cm)
侧面积:25.12×(14-8)=150.72(cm2)
表面积:3.14×(8÷2)2×2+150.72=251.2(cm2)
第3课时 圆柱的表面积(2)
一、1.C 2.A 3.B 4.C 5.D
二、1.(15×10+15×8+10×8)×2=700(cm2)
2.r=31.4÷3.14÷2=5(cm) 2×3.14×5×(5+8)=408.2(cm2)
三、1.12×4+8×4+18=98(cm) 2.3.14×8×12=301.44(cm2)
3.r=8÷2=4(cm) 2×3.14×4×(4+12)=401.92(cm2)
四、r=6÷2=3(m)
S一底一侧=πr(r+2h)=3.14×3×(3+2×1.5)=56.52(m2)
五、10÷2=5(dm) 8÷2=4(dm)
2×3.14×5×(5+2)+3.14×8×12-3.14×42=471(dm2)=4.71(m2)
六、3.14×(1+1)2+3.14×1×2×1=18.84(dm2)
第4课时 圆柱的体积(1)
一、1.长方体 底面积 高 底面积 高 底面积 高 πr2h 2.251.2 3.6
二、1.C 2.B
三、1.3.14×62×15=1695.6(cm3) 2.25×4=100(cm3)
3.r=25.12÷3.14÷2=4(cm) h=4×1.5=6(cm)
V=3.14×42×6=301.44(cm3)
四、1.2÷2=1(m) 3.14×12×5=15.7(m3)
2.1m=10dm 3.14×52×10=785(L) 785×20=15700(元)
五、216÷4=54(cm2) 1m=100cm 54×100=5400(cm3)
六、60÷2÷10=3(cm) 3.14×32×10=282.6(cm3)
第5课时 圆柱的体积(2)
一、1.表面积 容积 2.450 390 750 0.75 3.2 125.6 4.9
二、1.C 2.A 3.A
三、
圆
柱
底面半径
底面周长
高
表面积
体积
2cm
12.56cm
4cm
75.36cm2
50.24cm3
3dm
18.84dm
2dm
94.2dm2
56.52dm3
5m
31.4m
3m
251.2m2
235.5m3
四、1.1800÷12×20=3000(cm3) 2.20×8×6÷(6+2)=120(mL)
3.2m=200cm 3.14×(20÷2)2×200÷5=12560(个)
五、C=62.8÷5=12.56(cm) r=12.56÷3.14÷2=2(cm)
V=3.14×22×(20-5)=188.4(cm3)
第6课时 圆柱的体积(3)
一、水 空余部分 不变 形状 水 空余部分
3.14×(8÷2)2×10=502.4(cm3)
3.14×(8÷2)2×2.5=125.6(cm3)
502.4+125.6=628(cm3)=628(mL)
二、1.30 2.15072
三、3.14×(8÷2)2×10=502.4(mL)
四、1.20÷2=10(cm) 10÷2=5(cm) 3.14×(102-52)×40=9420(cm3)
2.6÷2=3(cm) 141.3÷(3.14×32)=5(cm) 8-5=3(cm)
五、10÷(20+5)×20=8(L)
六、A A 大
第1课时 圆柱的认识
一、填一填。
1.圆柱是由( )个面围成的。圆柱的上、下两个面叫做( ),它们是相等的两个( ),圆柱周围的面(上、下底面除外)叫做( )。
2.圆柱的两个底面之间的( )叫做圆柱的高,圆柱的高有( )条。
二、请你在圆柱的下面画“○”。
( ) ( ) ( )
( ) ( ) ( )
三、折一折,想一想,能得到什么图形?写在括号里。
( ) ( ) ( )
四、选一选。(将正确答案的序号填在括号里)
1.下图中,图( )中的线段表示的是圆柱的高。
A B C
2.下面各图中,图( )是圆柱的展开图。
A B C
3.如下图,把下面的立体图形切开,图( )切开后的形状是圆。
A B C
五、分别转动长方形的长和宽形成下面的两个圆柱。(教材P18做一做第2题变式题)
1.圆柱甲是以( )边为轴旋转而成的,高是( )cm,底面半径是( )cm,底面积是(50.24)cm2。
2.圆柱乙是以( )边为轴旋转而成的,高是( )cm,底面半径是( )cm,底面积是( )cm2。
六、一个圆柱的侧面展开图是一个正方形,那么这个圆柱的高与它的底面直径的比是( )。
A.1∶π B.π∶1 C.2π∶1
第2课时 圆柱的表面积(1)
一、填一填。
1.
如图,把圆柱的侧面沿某条高剪开,得到一个长方形。这个长方形的长等于圆柱的(底面周长),宽等于圆柱的( )。因为长方形的面积=长×宽,所以圆柱的侧面积=( )×( ),用字母表示为S侧=( )。
2.圆柱的表面积=( )+( )×2
3.用一张长30cm,宽20cm的长方形纸围成一个最大的圆柱,这个圆柱的侧面积是( )cm2。
二、求下面各圆柱的侧面积。
1.底面周长是25cm,高8cm。
2.底面半径3cm,高5cm。
3.底面直径2.5cm,高4cm。
三、求下面圆柱的表面积。(单位:cm)
1. 2.
四、解决问题。
1.一台压路机的前轮是圆柱形,轮宽2m,底面直径是1.5m,前轮转动一周,压路的面积是多少平方米?转动5周呢?
2.小昕给自己的保温杯做一个布套(全套上),保温杯的底面直径是8cm,高是16cm,做这个布套至少需要多少布料?
五、有一张长方形纸板(如下图),剪下涂色部分围成一个圆柱,求这个圆柱的表面积。
第3课时 圆柱的表面积(2)
一、下面这些生活中的实际问题是求圆柱的什么?把字母填在相应的括号里。
1.压路机滚筒转动一周的压路面积。( )
2.圆柱形水池的占地面积。( )
3.做一个无盖圆柱形铁皮水桶需多少铁皮?( )
4.做圆柱形通风管需要多少铁皮?( )
5.做一个圆柱形铁皮蓄水罐需要多少铁皮?( )
A.求底面积
B.求一个底面积与侧面积的和
C.求侧面积
D.求两个底面积与侧面积的和
二、求下面各立体图形的表面积。(单位:cm)
1. 2.
三、一个圆柱形铁皮礼品盒,高12cm,底面直径8cm。用塑料绳扎成如下图的形状,打结处用去绳子18cm。
1.一共用去塑料绳多少厘米?
2.在这个礼品盒的侧面贴一张包装广告纸,这张纸的面积是多少?
3.做这个礼品盒至少需要多少平方厘米的铁皮?
四、一个圆柱形水池,它的直径是6m,池深1.5m,在水池内壁和底面都要贴上瓷砖。贴瓷砖的面积是多少平方米?
五、如图,要给一根立在地上的铁柱子刷上油漆(下面的圆柱的底面不刷漆),一共要刷多少平方米?
六、有一顶帽子(如图),帽顶部分是圆柱形,用花布做的,帽檐部分是一个圆环,也是用同样的花布做的,已知帽顶的底面半径、高和帽檐宽都是1dm,那么做这顶帽子至少要用多少平方分米的花布?
第4课时 圆柱的体积(1)
填一填。
1.
如图,为了推导圆柱的体积,我们可以将圆柱转化为近似的( ),转化后这个图形的底面积等于圆柱的( ),高等于圆柱的( ),因为长方体的体积=( )×( ),所以圆柱的体积=( )×( )。如果底面半径用r表示,高用h表示,那么圆柱的体积计算公式为V=( )。
2.一个圆柱的底面半径是4cm,高是5cm,这个圆柱的体积是( )cm3。
3.一个圆柱的体积是360cm3,底面积是60cm2,高是( )cm。
二、选一选。(将正确答案的序号填在括号里)
1.等底等高的圆柱和长方体,它们的体积相比较,( )。
A.圆柱的体积大 B.长方体的体积大
C.一样大
2.将一个圆柱通过切、拼,转化成一个近似的长方体,在这个过程中,( )。
A.表面积和体积都不变
B.体积不变,表面积变大
C.表面积不变,体积变大
三、求下面圆柱的体积。
1.
2.圆柱的底面积是25cm2,高是4cm。
3.圆柱的底面周长是25.12cm,高是半径的1.5倍。
四、解决问题。
1.一口圆柱形水井,井水深5m,底面直径为2m,现在井内有水多少立方米?
2.一个装满酒的圆柱形酒桶,从里面量,它的底面半径是5dm,高为1m。如果每升酒按20元计算,这桶酒价值多少钱?
五、有一根长1m的圆柱形钢材,把它截成三段后,表面积比原来增加216cm2,这根钢材原来的体积是多少立方厘米?
六、把一个高是10cm的圆柱按下图切开,拼成近似的长方体,表面积增加了60cm2。圆柱的体积是多少立方厘米?
第5课时 圆柱的体积(2)
一、填一填。
1.做一个圆柱形铁皮罐头盒,求需要多少铁皮,是求罐头盒的(表面积);求罐头盒可以容纳多少物体,是求罐头盒的( )。
2.0.45L=( )cm3 3.9m3=( )L
750cm3=( )mL=( )dm3
3.一个圆柱的侧面积是125.6cm2,高是10cm,它的底面半径是( )cm,体积是( )cm3。
4.一个圆柱的高不变,底面半径扩大到原来的3倍,体积会扩大到原来的( )倍。
二、选一选。(将正确答案的序号填在括号里)
1.两个体积相等的圆柱,它们一定是( )。
A.底面积和高都相等
B.底面积相等,高不相等
C.底面积和高的乘积相等
2.一个圆柱形水桶底面积是15dm2,容积是120L,高是( )dm。
A.8 B.0.8 C.18
3.把一个棱长是4dm的正方体木块削成一个最大的圆柱,这个圆柱的体积是( )dm3。
A.50.24 B.64 C.100.48
三、填表。
四、解决问题。
1.有两个底面积相等的圆柱,一个圆柱的高是12cm,体积是1800cm3,另一个圆柱的高是20cm,它的体积是多少?
1800÷12×20=3000(cm3)
答:它的体积是3000cm3。
2.周末,小明请六位小朋友来家做客,妈妈准备了一盒果汁,正好可以倒满下面这种杯子6杯,如果让每位小朋友、小明和妈妈每人都喝上果汁,平均每人倒多少毫升?
3.一段长2m的圆柱形钢材,底面直径是20cm。如果加工一个汽车零件要用去钢材5cm3。这段钢材能生产多少个这种零件?
2m=200cm
五、如图,一个圆柱的高增加5cm后,圆柱的表面积增加了62.8cm2。求原圆柱的体积是多少立方厘米?
第6课时 圆柱的体积(3)
一、一个瓶子的内直径是8cm,装入10cm高的水后,盖好瓶盖倒过来放平(如图),量得空余部分的高是2.5cm,这个瓶子的容积是多少毫升?
水的体积:
________________________________________________________________________
空余部分的体积:
________________________________________________________________________
________________________________________________________________________
瓶子的容积:
________________________________________________________________________
________________________________________________________________________
答:这个瓶子的容积是( )mL。
二、填一填。
1.一块不规则的石头,放在装有100mL水的量杯内(石头完全浸没在水中),结果量杯中的水面上升到130mL处,这块不规则的石头的体积是( )mL。
2.一根圆柱形水管的内直径是4cm,水管里的水流动速度是每秒20cm,每分钟流过水管的水有( )mL。
三、一瓶装满的酱油,妈妈炒菜用去了一些后酱油高15cm。把瓶盖拧紧后倒置放平,空余部分高10cm,瓶内直径是8cm。妈妈炒菜用了多少酱油?
四、看图计算。
1.下图是一根空心钢管,求空心钢管的体积。(单位:cm)
2.鲜奶倒进杯子里后,奶面离杯口还有几厘米?
五、一个容积为10L的油壶,壶中油深20cm。把油壶盖拧紧倒立放平,这时瓶中空余部分高5cm,壶中装有油多少升?
六、下面三个图形的面积都是24cm2。把这些图形分别卷成圆柱,卷成的圆柱体积最小的是(A),体积最大的是(A)。(单位:cm)
答案
第1课时 圆柱的认识
一、 1.3 底面 圆 侧面 2.距离 无数
二、(○) () (○) () () (○)
三、长方体 圆柱 正方体
四、1.A 2.C 3.B
五、1.AD或BC 2 4 50.24 2.AB或CD 4 2 12.56
六、B
第2课时 圆柱的表面积(1)
一、1.底面周长 高 底面周长 高 Ch2.侧面积 底面积 3.600
二、1.S侧=Ch=25×8=200(cm2)
2.S侧=2πrh=2×3.14×3×5=94.2(cm2)
3.S侧=πdh=3.14×2.5×4=31.4(cm2)
三、1.S表=2πr2+2πrh=2×3.14×82+2×3.14×8×5=653.12(cm2)
2.r=d÷2=6÷2=3(cm)
S表=2πr2+2πrh=2×3.14×32+2×3.14×3×10=244.92(cm2)
四、1.1.5×3.14×2=9.42(m2) 9.42×5=47.1(m2)
2.2×3.14×(8÷2)2+8×3.14×16=502.4(cm2)
五、底面直径:25.12÷3.14=8(cm)
侧面积:25.12×(14-8)=150.72(cm2)
表面积:3.14×(8÷2)2×2+150.72=251.2(cm2)
第3课时 圆柱的表面积(2)
一、1.C 2.A 3.B 4.C 5.D
二、1.(15×10+15×8+10×8)×2=700(cm2)
2.r=31.4÷3.14÷2=5(cm) 2×3.14×5×(5+8)=408.2(cm2)
三、1.12×4+8×4+18=98(cm) 2.3.14×8×12=301.44(cm2)
3.r=8÷2=4(cm) 2×3.14×4×(4+12)=401.92(cm2)
四、r=6÷2=3(m)
S一底一侧=πr(r+2h)=3.14×3×(3+2×1.5)=56.52(m2)
五、10÷2=5(dm) 8÷2=4(dm)
2×3.14×5×(5+2)+3.14×8×12-3.14×42=471(dm2)=4.71(m2)
六、3.14×(1+1)2+3.14×1×2×1=18.84(dm2)
第4课时 圆柱的体积(1)
一、1.长方体 底面积 高 底面积 高 底面积 高 πr2h 2.251.2 3.6
二、1.C 2.B
三、1.3.14×62×15=1695.6(cm3) 2.25×4=100(cm3)
3.r=25.12÷3.14÷2=4(cm) h=4×1.5=6(cm)
V=3.14×42×6=301.44(cm3)
四、1.2÷2=1(m) 3.14×12×5=15.7(m3)
2.1m=10dm 3.14×52×10=785(L) 785×20=15700(元)
五、216÷4=54(cm2) 1m=100cm 54×100=5400(cm3)
六、60÷2÷10=3(cm) 3.14×32×10=282.6(cm3)
第5课时 圆柱的体积(2)
一、1.表面积 容积 2.450 390 750 0.75 3.2 125.6 4.9
二、1.C 2.A 3.A
三、
圆
柱
底面半径
底面周长
高
表面积
体积
2cm
12.56cm
4cm
75.36cm2
50.24cm3
3dm
18.84dm
2dm
94.2dm2
56.52dm3
5m
31.4m
3m
251.2m2
235.5m3
四、1.1800÷12×20=3000(cm3) 2.20×8×6÷(6+2)=120(mL)
3.2m=200cm 3.14×(20÷2)2×200÷5=12560(个)
五、C=62.8÷5=12.56(cm) r=12.56÷3.14÷2=2(cm)
V=3.14×22×(20-5)=188.4(cm3)
第6课时 圆柱的体积(3)
一、水 空余部分 不变 形状 水 空余部分
3.14×(8÷2)2×10=502.4(cm3)
3.14×(8÷2)2×2.5=125.6(cm3)
502.4+125.6=628(cm3)=628(mL)
二、1.30 2.15072
三、3.14×(8÷2)2×10=502.4(mL)
四、1.20÷2=10(cm) 10÷2=5(cm) 3.14×(102-52)×40=9420(cm3)
2.6÷2=3(cm) 141.3÷(3.14×32)=5(cm) 8-5=3(cm)
五、10÷(20+5)×20=8(L)
六、A A 大
