八年级数学下册9.5三角形的中位线作业设计含答案(新版)苏科版
文档属性
| 名称 | 八年级数学下册9.5三角形的中位线作业设计含答案(新版)苏科版 | 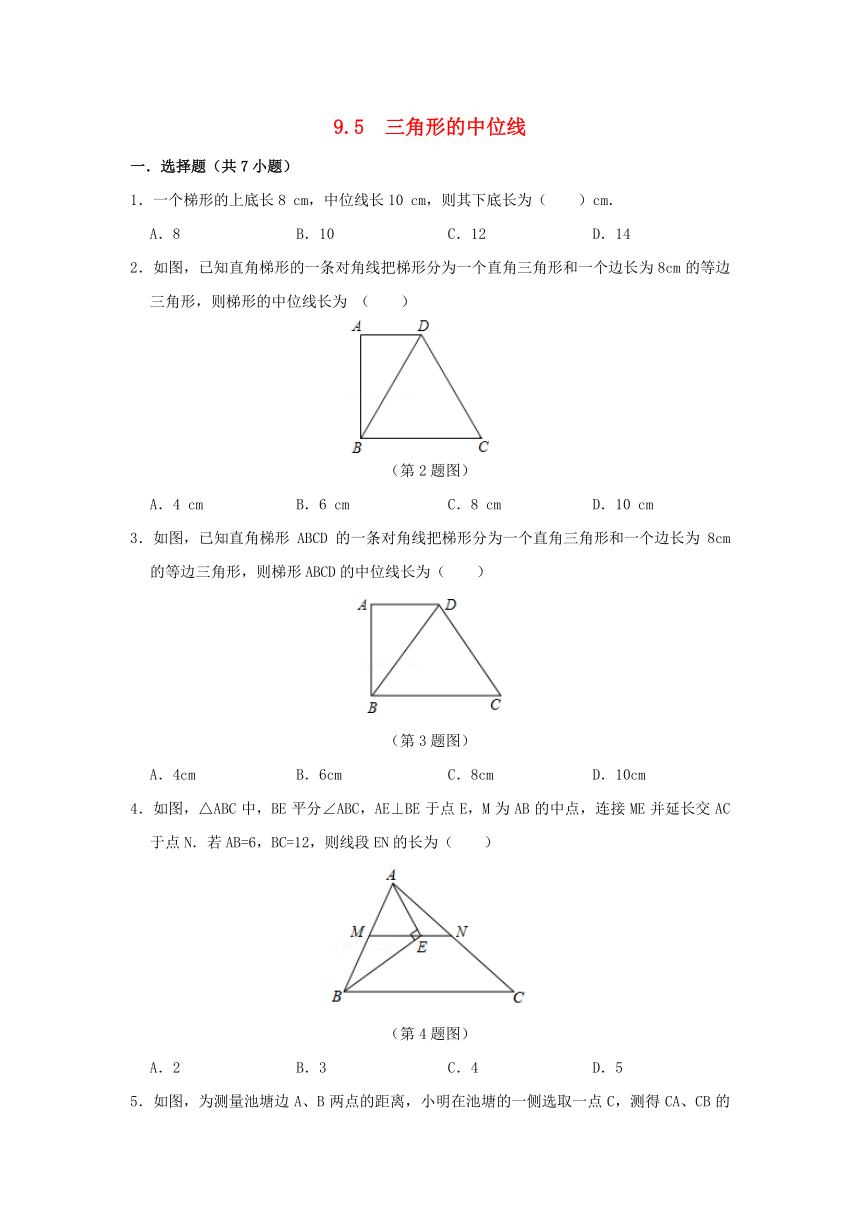 | |
| 格式 | zip | ||
| 文件大小 | 102.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 14:02:53 | ||
图片预览

文档简介
9.5 三角形的中位线
一.选择题(共7小题)
1.一个梯形的上底长8 cm,中位线长10 cm,则其下底长为( )cm.
A.8 B.10 C.12 D.14
2.如图,已知直角梯形的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形的中位线长为 ( )
(第2题图)
A.4 cm B.6 cm C.8 cm D.10 cm
3.如图,已知直角梯形ABCD的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形ABCD的中位线长为( )
(第3题图)
A.4cm B.6cm C.8cm D.10cm
4.如图,△ABC中,BE平分∠ABC,AE⊥BE于点E,M为AB的中点,连接ME并延长交AC于点N.若AB=6,BC=12,则线段EN的长为( )
(第4题图)
A.2 B.3 C.4 D.5
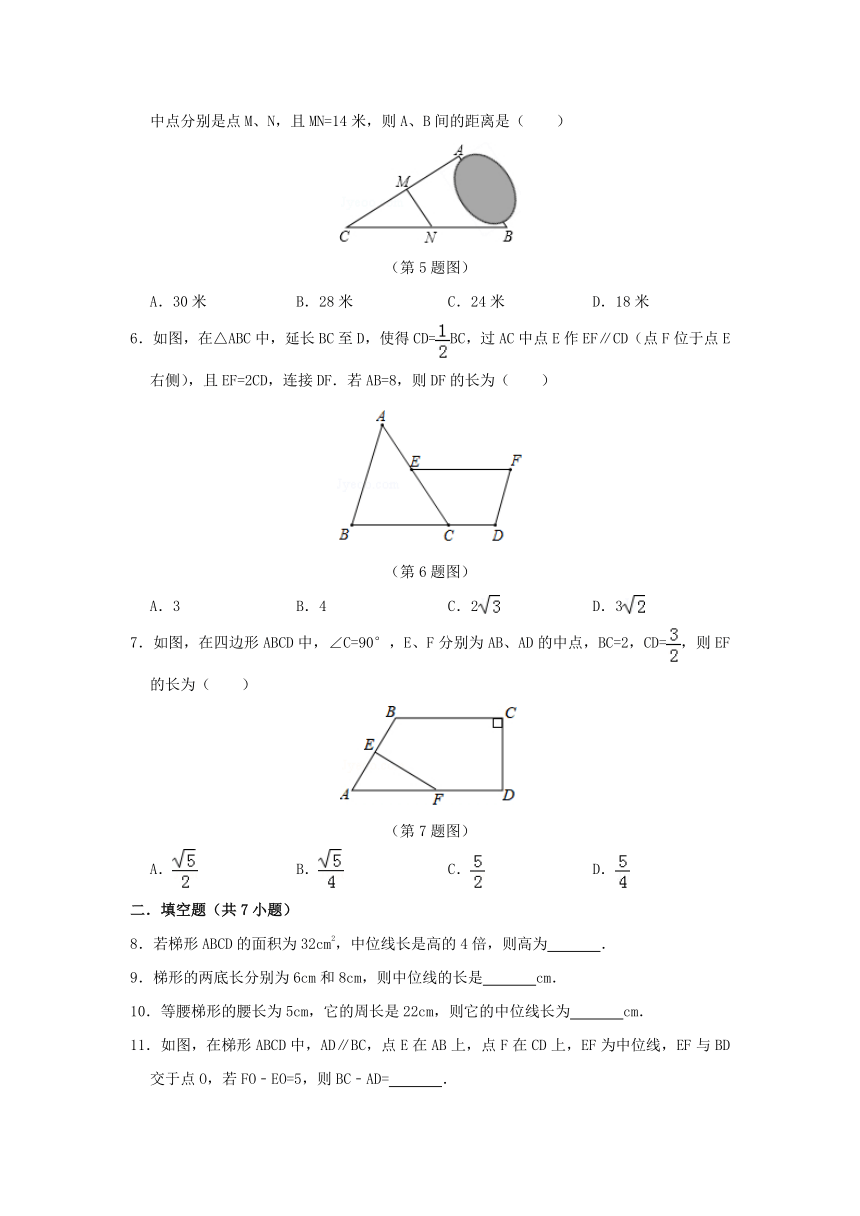
5.如图,为测量池塘边A、B两点的距离,小明在池塘的一侧选取一点C,测得CA、CB的中点分别是点M、N,且MN=14米,则A、B间的距离是( )
(第5题图)
A.30米 B.28米 C.24米 D.18米
6.如图,在△ABC中,延长BC至D,使得CD=BC,过AC中点E作EF∥CD(点F位于点E右侧),且EF=2CD,连接DF.若AB=8,则DF的长为( )
(第6题图)
A.3 B.4 C.2 D.3
7.如图,在四边形ABCD中,∠C=90°,E、F分别为AB、AD的中点,BC=2,CD=,则EF的长为( )
(第7题图)
A. B. C. D.
二.填空题(共7小题)
8.若梯形ABCD的面积为32cm2,中位线长是高的4倍,则高为 .
9.梯形的两底长分别为6cm和8cm,则中位线的长是 cm.
10.等腰梯形的腰长为5cm,它的周长是22cm,则它的中位线长为 cm.
11.如图,在梯形ABCD中,AD∥BC,点E在AB上,点F在CD上,EF为中位线,EF与BD交于点O,若FO﹣EO=5,则BC﹣AD= .
(第11题图)
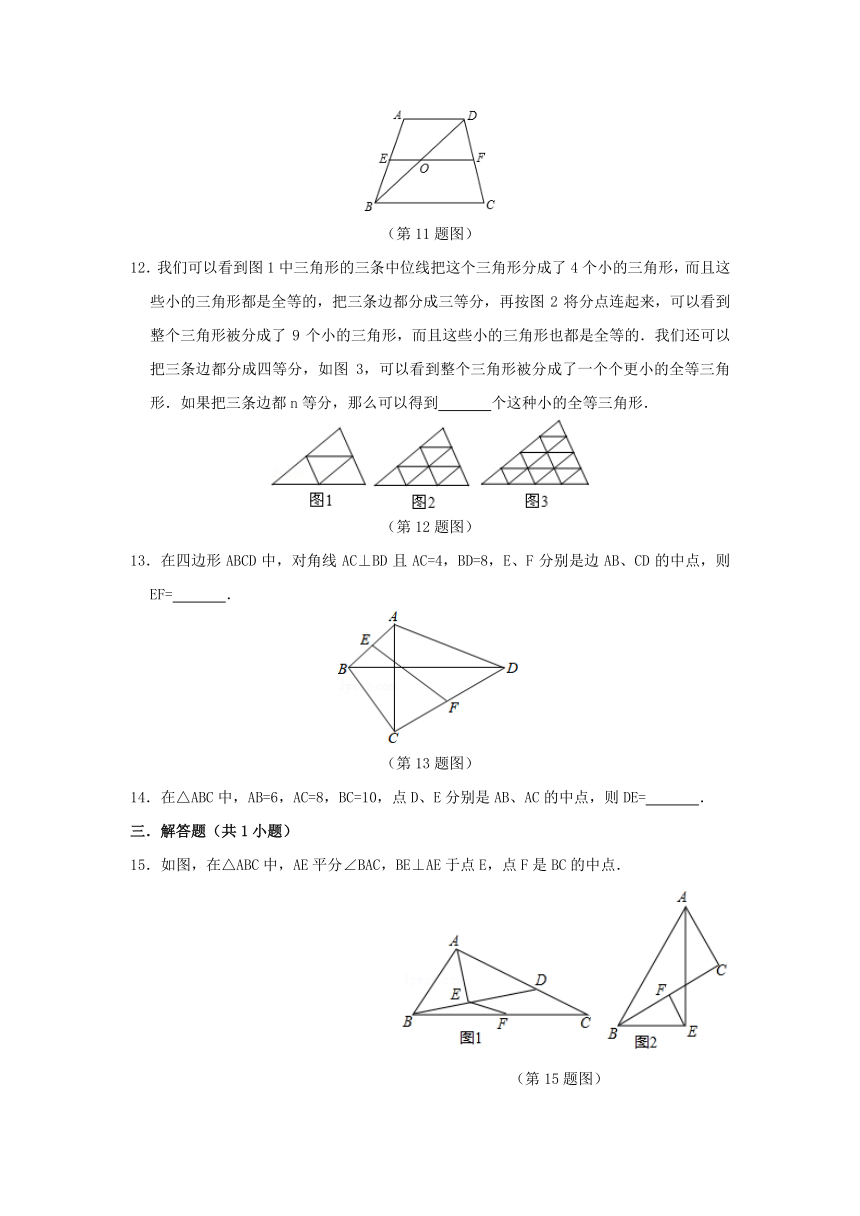
12.我们可以看到图1中三角形的三条中位线把这个三角形分成了4个小的三角形,而且这些小的三角形都是全等的,把三条边都分成三等分,再按图2将分点连起来,可以看到整个三角形被分成了9个小的三角形,而且这些小的三角形也都是全等的.我们还可以把三条边都分成四等分,如图3,可以看到整个三角形被分成了一个个更小的全等三角形.如果把三条边都n等分,那么可以得到 个这种小的全等三角形.
(第12题图)
13.在四边形ABCD中,对角线AC⊥BD且AC=4,BD=8,E、F分别是边AB、CD的中点,则EF= .
(第13题图)
14.在△ABC中,AB=6,AC=8,BC=10,点D、E分别是AB、AC的中点,则DE= .
三.解答题(共1小题)
15.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(第15题图)
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC﹣AB);
(2)如图2,请直接写出线段AB、AC、EF的数量关系.
参考答案
一.1.C 2.B 3.B 4.B 5.B 6.B 7.D
二.8.2 9.7 10.6 11.10 12.n2 13.2 14.5
三.15.(1)证明:如答图1.
∵AE⊥BD,
∴∠AED=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠DAE+∠ADE=90°.
∵∠BAE=∠DAE,
∴∠ABE=∠ADE,
∴AB=AD.
∵AE⊥BD,
∴BE=DE.
∵BF=FC,
∴EF=DC==(AC﹣AB).
(2)结论:EF=(AB﹣AC),
理由:如图2中,延长AC交BE的延长线于点P.
(第15题答图)
∵AE⊥BP,
∴∠AEP=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠PAE+∠APE=90°.
∵∠BAE=∠PAE,
∴∠ABE=∠ADE,
∴AB=AP.
∵AE⊥BD,
∴BE=PE.
∵BF=FC,
∴EF=PC=(AP﹣AC)=(AB﹣AC).
一.选择题(共7小题)
1.一个梯形的上底长8 cm,中位线长10 cm,则其下底长为( )cm.
A.8 B.10 C.12 D.14
2.如图,已知直角梯形的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形的中位线长为 ( )
(第2题图)
A.4 cm B.6 cm C.8 cm D.10 cm
3.如图,已知直角梯形ABCD的一条对角线把梯形分为一个直角三角形和一个边长为8cm的等边三角形,则梯形ABCD的中位线长为( )
(第3题图)
A.4cm B.6cm C.8cm D.10cm
4.如图,△ABC中,BE平分∠ABC,AE⊥BE于点E,M为AB的中点,连接ME并延长交AC于点N.若AB=6,BC=12,则线段EN的长为( )
(第4题图)
A.2 B.3 C.4 D.5
5.如图,为测量池塘边A、B两点的距离,小明在池塘的一侧选取一点C,测得CA、CB的中点分别是点M、N,且MN=14米,则A、B间的距离是( )
(第5题图)
A.30米 B.28米 C.24米 D.18米
6.如图,在△ABC中,延长BC至D,使得CD=BC,过AC中点E作EF∥CD(点F位于点E右侧),且EF=2CD,连接DF.若AB=8,则DF的长为( )
(第6题图)
A.3 B.4 C.2 D.3
7.如图,在四边形ABCD中,∠C=90°,E、F分别为AB、AD的中点,BC=2,CD=,则EF的长为( )
(第7题图)
A. B. C. D.
二.填空题(共7小题)
8.若梯形ABCD的面积为32cm2,中位线长是高的4倍,则高为 .
9.梯形的两底长分别为6cm和8cm,则中位线的长是 cm.
10.等腰梯形的腰长为5cm,它的周长是22cm,则它的中位线长为 cm.
11.如图,在梯形ABCD中,AD∥BC,点E在AB上,点F在CD上,EF为中位线,EF与BD交于点O,若FO﹣EO=5,则BC﹣AD= .
(第11题图)
12.我们可以看到图1中三角形的三条中位线把这个三角形分成了4个小的三角形,而且这些小的三角形都是全等的,把三条边都分成三等分,再按图2将分点连起来,可以看到整个三角形被分成了9个小的三角形,而且这些小的三角形也都是全等的.我们还可以把三条边都分成四等分,如图3,可以看到整个三角形被分成了一个个更小的全等三角形.如果把三条边都n等分,那么可以得到 个这种小的全等三角形.
(第12题图)
13.在四边形ABCD中,对角线AC⊥BD且AC=4,BD=8,E、F分别是边AB、CD的中点,则EF= .
(第13题图)
14.在△ABC中,AB=6,AC=8,BC=10,点D、E分别是AB、AC的中点,则DE= .
三.解答题(共1小题)
15.如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(第15题图)
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=(AC﹣AB);
(2)如图2,请直接写出线段AB、AC、EF的数量关系.
参考答案
一.1.C 2.B 3.B 4.B 5.B 6.B 7.D
二.8.2 9.7 10.6 11.10 12.n2 13.2 14.5
三.15.(1)证明:如答图1.
∵AE⊥BD,
∴∠AED=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠DAE+∠ADE=90°.
∵∠BAE=∠DAE,
∴∠ABE=∠ADE,
∴AB=AD.
∵AE⊥BD,
∴BE=DE.
∵BF=FC,
∴EF=DC==(AC﹣AB).
(2)结论:EF=(AB﹣AC),
理由:如图2中,延长AC交BE的延长线于点P.
(第15题答图)
∵AE⊥BP,
∴∠AEP=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠PAE+∠APE=90°.
∵∠BAE=∠PAE,
∴∠ABE=∠ADE,
∴AB=AP.
∵AE⊥BD,
∴BE=PE.
∵BF=FC,
∴EF=PC=(AP﹣AC)=(AB﹣AC).
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
