人教版七年级数学下册5.3平行线的性质同步测试(有答案)
文档属性
| 名称 | 人教版七年级数学下册5.3平行线的性质同步测试(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 273.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 00:00:00 | ||
图片预览


文档简介
绝密★启用前
5.3 平行线的性质
班级: 姓名:
1.如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )
A.70° B.40° C.35° D.30°
2.如图,已知AB∥CD,∠B=100°,EF平分∠BEC,EG⊥EF,则∠DEG等于( )
A.50° B.40° C.60° D.70°
3.如图所示,已知AB∥CD,∠A=55°,∠C=20°,则∠P的度数是( )
A.55° B.75° C.35° D.125°
4.如图,,A.B为直线上两点,C、D为直线上两点,则与的面积大小关系是( )
A.
B.
C.
D.不能确定
5.如图,直线AB∥ CD,∠ B=50°,∠ C=40°,则∠E等于( )
A.70° B.80° C.90° D.100°
6.如图,已知,,垂足为E,若,则的度数为______.
7.如图,直线,直线EF与AB、CD相交于点E、F,的平分线EN与CD相交于点若,则_____.
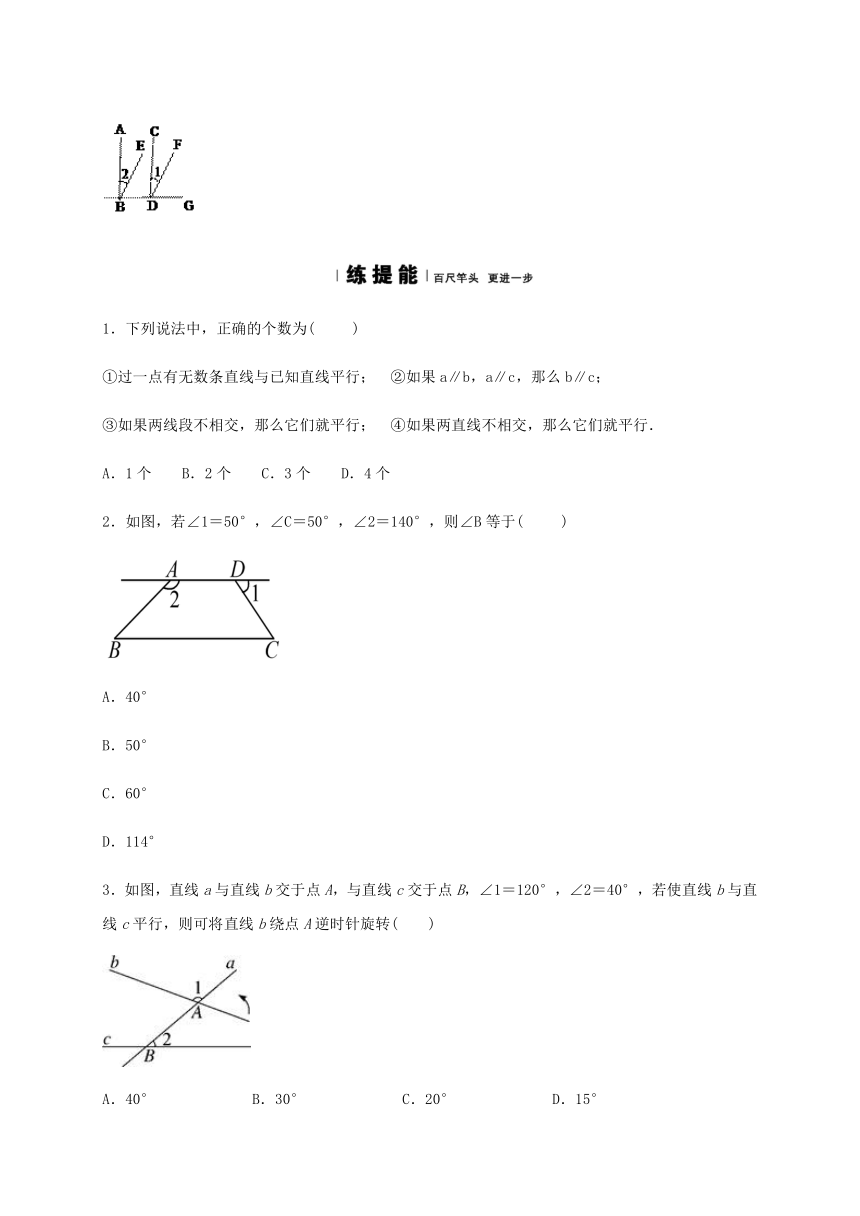
8.如图,已知点B,D,G在同一条直线上,AB∥CD,∠1=∠2,请问BE与DF平行吗?为什么?
1.下列说法中,正确的个数为( )
①过一点有无数条直线与已知直线平行; ②如果a∥b,a∥c,那么b∥c;
③如果两线段不相交,那么它们就平行; ④如果两直线不相交,那么它们就平行.
A.1个 B.2个 C.3个 D.4个
2.如图,若∠1=50°,∠C=50°,∠2=140°,则∠B等于( )
A.40°
B.50°
C.60°
D.114°
3.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )
A.40° B.30° C.20° D.15°
4.已知,直线EF分别交AB、CD于点G、H,∠EGB=25°,将一个60°角的直角三角尺如图放置(60°角的顶点与H重合),则∠PHG等于( )
A.30° B.35° C.40° D.45°
5.如图,直线a∥b,直线c是截线,如果∠1=50°,那么∠2等于(? )
?
A.150° B.140° C.130° D.120°
6.如图,如果AB∥CD,CD∥EF,∠1=36°, ∠2=76°那么∠BCE等于____________
7.如图,AB∥CD,试再添一个条件,使∠1=∠2成立,_____、_____、_____(要求给出三个以上答案)
8.在实践中学习:
(1)如图1所示:已知AB∥CD,∠ABD=115°,根据 可得出:∠BDC的度数是 .
(2)如图2所示:已知AB∥CD,∠ABC=25°,∠EDC=40°,求∠BED的度数.
(3)如图3所示:已知MA∥NC,试确定∠A、∠B、∠C和∠E、∠F的关系,并说明理由.
(4)如图4所示:已知AB∥CD,∠ABE=α,∠FCD=β,∠CFE=γ,且BE⊥EF,试确定α、β、γ的关系,请说明理由.
1.(2019·山西)如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB
于点D,交AC于点E,若∠1=145°,则∠2的度数是( )
A.30° B.35° C.40° D.45°
2.(2019·衡阳)如图,已知AB∥CD,AF交CD于点E,且BE⊥AF,∠BED=40°,则∠A的度数是( )
A. 45° B. 50° C. 80° D. 90°
3.(2019·凉山) 如图,BD∥EF, AE 与 BD 交于点 C,∠B=30°,∠A=75°,则 ∠E的度数为( )
A. 135° B.125° C. 115° D.105°
4. (2019·泰安) 如图,直线l1∥l2,∠1=30°,则∠2+∠3=( )
A.150° B.180° C.210° D.240°
参考答案
1-5.CACBC
6.40°
7.
8.解:BE∥DF,.理由如下:
∵AB∥CD,
∴∠ABG=∠CDG
∵∠1=∠2,
∴∠ABG-∠2=∠CDG-∠1,即∠EBG=∠FDG
∴BE∥DF.
1-5.AACBC
6.140°
7.CF//BE ∠E=∠F ∠FCB=∠EBC
8.解:(1)∵AB∥CD,
∴∠ABD+∠BDC=180°,
∴∠BDC=180°-115°=65°;
(2)过点E作EF∥AB
∵AB∥CD(已知)∴EF∥CD
∵EF∥AB,EF∥CD
∴∠ABC=∠BEF,∠EDC=∠DEF,
∴∠BEF=25°,∠DEF=40°
即∠BED=65°;
(3)∠A、∠B、∠C和∠E、∠F的关系为∠E+∠F=∠A+∠B+∠C.理由如下:
作BH∥AM,如图3,
由(2)的结论得到∠E=∠1+∠A,∠F=∠2+∠C,
∴∠E+∠F=∠1+∠A+∠2+∠C=∠A+∠B+∠C;
(4)γ+α=90°+β.理由如下:
作BP∥AB,如图4,
由(2)的结论得∠ABE+∠EFP=∠BEF,
而∠PFC=∠FCD,
∴∠EFP=90°-α,∠PFC=β,
∴∠EFP+∠PFC=90°-α+β,
∴γ=90°-α+β,
即γ+α=90°+β.
1-4.CBDC
