6.1 同底数幂的乘法 说课课件(14张PPT)
文档属性
| 名称 | 6.1 同底数幂的乘法 说课课件(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 137.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
一、教材分析
二、教学方法和手段
三、学法指导
四、教学流程图
五、教学过程
六、板书设计
一
二
三
四
五
六
1
.教材的地位和作用:
2
.教学重点和难点:
3
.学习目标:
重点:同底数幂相除法则的推导及法则本身的理解;
难点:灵活应用同底数幂的相除法则来解决问题。
①知识目标:
②能力目标:
③情感目标:
一、教材分析
二、教学方法和手段
创设深重熟悉的问题情境,采用探索式、启发式等方法进行教学;
鼓励学生自主探究和小组合作交流;
引导学生观察、归纳、探索;
培养学生分析、解决问题的能力;
采用分层教学模式组织教学。
三、学法指导
学生自主参与整堂课的知识建构,人人尝试问题的发现与解决;
互相合作解决问题;
归纳概括,形成能力;
学生始终处于主动猜想、主动探索状态;
养成及时归纳总结的良好习惯。
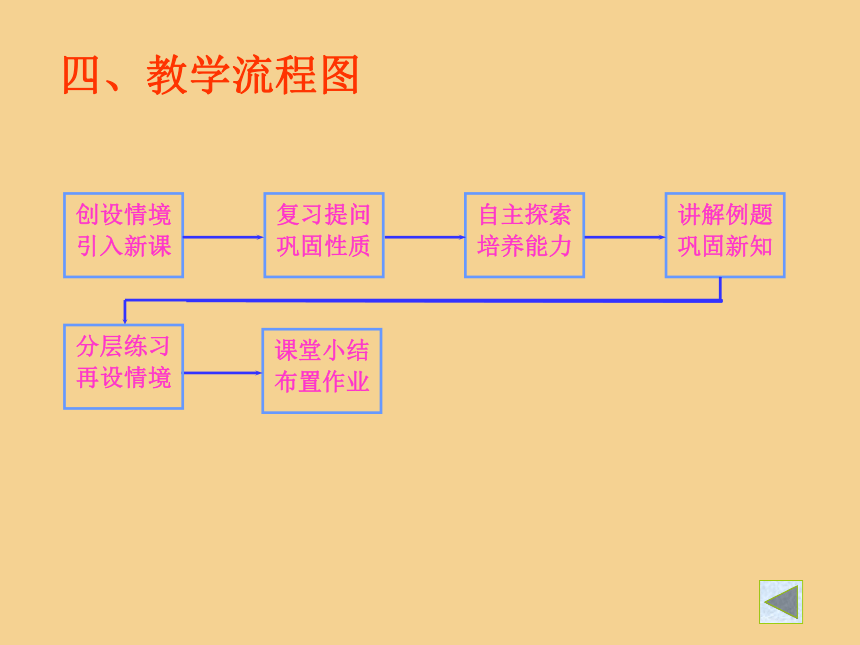
四、教学流程图
创设情境
引入新课
复习提问
巩固性质
自主探索
培养能力
讲解例题
巩固新知
课堂小结
布置作业
分层练习
再设情境
五、教学过程
1.创设情境,引入新课
2.复习提问,巩固性质
3.自主探索,培养能力
4.讲解例题,巩固新知
5.分层练习,再设情境
6.课堂小结,布置作业
1
2
3
4
5
6
1.创设情境,引入新课
引例:一种液体每升含有1012个有害细菌。为了试验某种杀菌剂的效果,科学家们进行了实验,发现1滴杀菌剂可以杀死109个此种细菌。要将1升液体中的有害细菌全部杀死,需要这种杀菌剂多少滴?你是怎样计算的?
1012÷109
(1)1012÷109=1
000
000
000
000÷1
000
000
000=1
000;
(3)1012÷109=103=1
000。
(2)1012÷109= =1
000;
2.复习提问,巩固性质
问题:同底数幂的乘法法则是什么?
可用怎样的公式进行表示?
如何说明它是正确的?
同底数的幂相乘,底数不变,指数相加。
am·an=am+n(m,n都是正整数)
…
…
3.自主探索,培养能力
计算下列各式,并说明理由(m>n):
(1)
105
÷103
; (2)
(–3)4÷(–3)2
;
(3)
a6÷a2(a≠0)
。
同底数的幂相除,底数不变,指数相减。
…
…
…
4.讲解例题,巩固新知
例1 计算:
(1)a7÷a4;
(2)(-x)6÷(-x)3;
(3)(xy)4÷(xy);
(4)
(3x2)5÷
(3x2)3
。
5.分层练习,再设情境
①下面的计算是否正确?如有错误请改正:
(1)a6÷a=a6;
(2)b6÷b3=b2;
(3)a10÷a9=a;
(4)(-bc)4÷(-bc)2=-b2c2。
( )
( )
( )
( )
②以下各题,请选择其中4题进行(其中最后两题较难):
(1)213÷27;
(2)(- )6÷(- )2;
(3)a11÷a5;
(4)(-x)7÷(-x);
(5)(-ab)5÷(-ab)2;
(6)62m+1÷6m;
(7)103÷103;
(8)22÷25。
6.课堂小结,布置作业
一个计算法则:
am÷an=am-n(a≠0,m,n都是正整数,m>n)
一个计算公式:
同底数幂相除,底数不变,指数相减。
六、板书设计
屏 幕
am×an=am+n(m,n都是正整数)
am÷an=am-n(a≠0,m,n都是正整数)
一、教材分析
二、教学方法和手段
三、学法指导
四、教学流程图
五、教学过程
六、板书设计
一
二
三
四
五
六
1
.教材的地位和作用:
2
.教学重点和难点:
3
.学习目标:
重点:同底数幂相除法则的推导及法则本身的理解;
难点:灵活应用同底数幂的相除法则来解决问题。
①知识目标:
②能力目标:
③情感目标:
一、教材分析
二、教学方法和手段
创设深重熟悉的问题情境,采用探索式、启发式等方法进行教学;
鼓励学生自主探究和小组合作交流;
引导学生观察、归纳、探索;
培养学生分析、解决问题的能力;
采用分层教学模式组织教学。
三、学法指导
学生自主参与整堂课的知识建构,人人尝试问题的发现与解决;
互相合作解决问题;
归纳概括,形成能力;
学生始终处于主动猜想、主动探索状态;
养成及时归纳总结的良好习惯。
四、教学流程图
创设情境
引入新课
复习提问
巩固性质
自主探索
培养能力
讲解例题
巩固新知
课堂小结
布置作业
分层练习
再设情境
五、教学过程
1.创设情境,引入新课
2.复习提问,巩固性质
3.自主探索,培养能力
4.讲解例题,巩固新知
5.分层练习,再设情境
6.课堂小结,布置作业
1
2
3
4
5
6
1.创设情境,引入新课
引例:一种液体每升含有1012个有害细菌。为了试验某种杀菌剂的效果,科学家们进行了实验,发现1滴杀菌剂可以杀死109个此种细菌。要将1升液体中的有害细菌全部杀死,需要这种杀菌剂多少滴?你是怎样计算的?
1012÷109
(1)1012÷109=1
000
000
000
000÷1
000
000
000=1
000;
(3)1012÷109=103=1
000。
(2)1012÷109= =1
000;
2.复习提问,巩固性质
问题:同底数幂的乘法法则是什么?
可用怎样的公式进行表示?
如何说明它是正确的?
同底数的幂相乘,底数不变,指数相加。
am·an=am+n(m,n都是正整数)
…
…
3.自主探索,培养能力
计算下列各式,并说明理由(m>n):
(1)
105
÷103
; (2)
(–3)4÷(–3)2
;
(3)
a6÷a2(a≠0)
。
同底数的幂相除,底数不变,指数相减。
…
…
…
4.讲解例题,巩固新知
例1 计算:
(1)a7÷a4;
(2)(-x)6÷(-x)3;
(3)(xy)4÷(xy);
(4)
(3x2)5÷
(3x2)3
。
5.分层练习,再设情境
①下面的计算是否正确?如有错误请改正:
(1)a6÷a=a6;
(2)b6÷b3=b2;
(3)a10÷a9=a;
(4)(-bc)4÷(-bc)2=-b2c2。
( )
( )
( )
( )
②以下各题,请选择其中4题进行(其中最后两题较难):
(1)213÷27;
(2)(- )6÷(- )2;
(3)a11÷a5;
(4)(-x)7÷(-x);
(5)(-ab)5÷(-ab)2;
(6)62m+1÷6m;
(7)103÷103;
(8)22÷25。
6.课堂小结,布置作业
一个计算法则:
am÷an=am-n(a≠0,m,n都是正整数,m>n)
一个计算公式:
同底数幂相除,底数不变,指数相减。
六、板书设计
屏 幕
am×an=am+n(m,n都是正整数)
am÷an=am-n(a≠0,m,n都是正整数)
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
