6.2 幂的乘方与积的乘方(1)课件(28张PPT)
文档属性
| 名称 | 6.2 幂的乘方与积的乘方(1)课件(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 348.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 00:00:00 | ||
图片预览





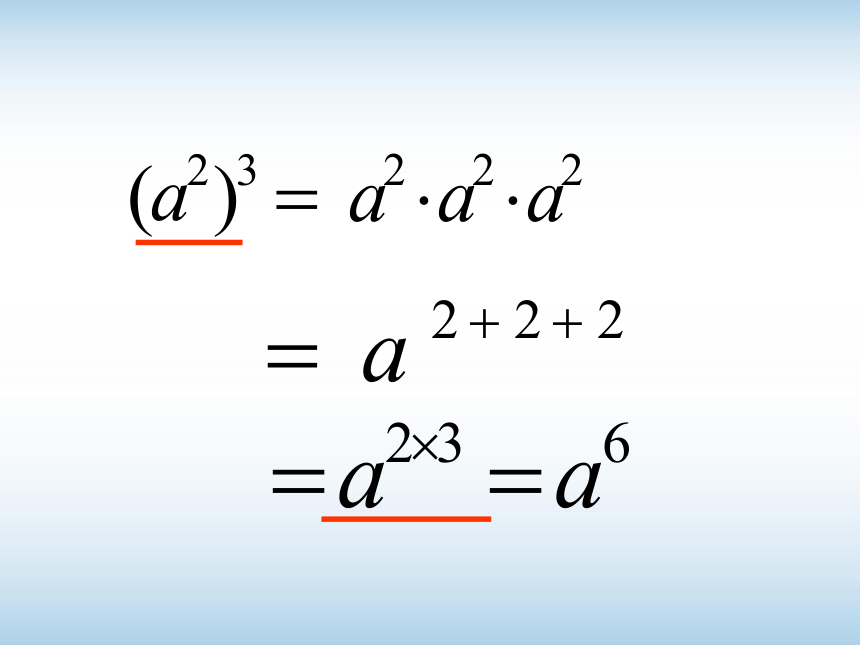


文档简介
(共28张PPT)
6.2.1
幂的乘方
复习
幂的意义:
a·a·
…
·a
n个a
=an
同底数幂乘法的运算性质:
am
·
an
=am+n
(m,n都是正整数)
练习
木星
太阳
地球
(102)3=106,为什么?
体积扩大的倍数比半径扩大的倍数大得多.
地球、木星、太阳可以近似地看作球体
.木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的
倍和
倍
103
106
(102)3
=102×102×102
=102+2+2
=102×3
=106
太棒了!
(根据
)
(根据
).
同底数幂的乘法性质
幂的意义
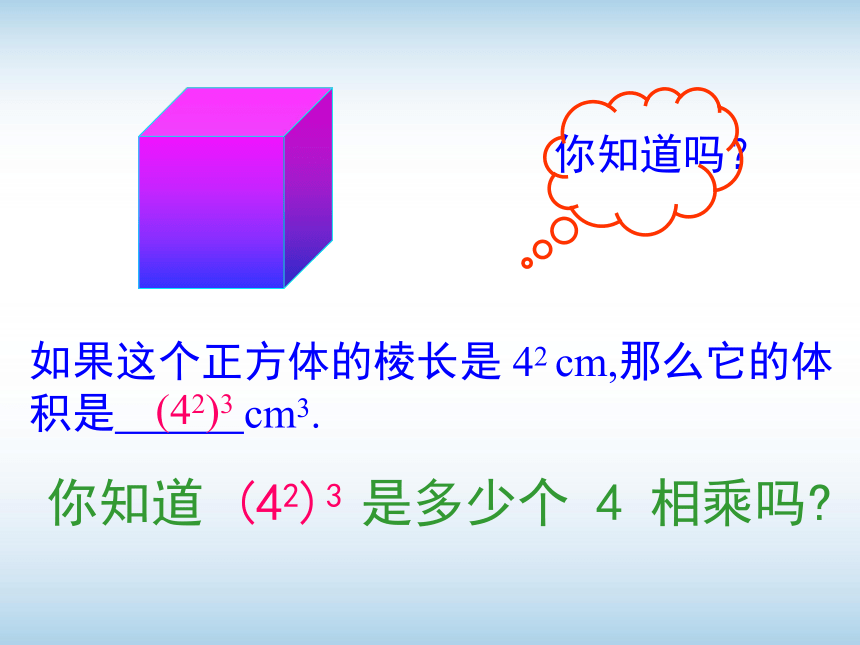
如果这个正方体的棱长是
42
cm,那么它的体积是 cm3.
你知道
(42)3
是多少个
4
相乘吗
你知道吗?
(42)3
想一想:
幂的乘方,底数变不变?
指数应怎样计算?
试计算:
其中m
,
n都是正整数
(am)n
=am·am·
…
·am
n个am
=am+m+
…
+m
n个m
=amn
(幂的意义)
(同底数幂的乘法性质)
(乘法的意义)
幂的乘方法则:
其中m
,
n都是正整数
这就是说:
幂的乘方,底数不变,
指数相乘。
例1
计算:
解:
例1
计算:
解:
例2
计算:
解:原式=
解:原式=
例3
把
化成
的形式。
解:
想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
幂的乘方法则:
(其中m,n都是正整数)
同底数幂的乘法法则:
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m,n都是正整数
底数不变
口答:
⑴
(a2)4
⑵(b3m)4
⑶
(xn)m
⑷
(b3)3
⑸
x4·x4
⑹
(x4)7
口答:
⑻
(a3)3
⑽
(x6)5
⑺
-(y7)2
⑾
[(x+y)3]4
⑼
[(-1)3]5
⑿
[(a+1)3]n
1.计算:
要认真呀!
⑴
(a2)3
⑵
a2·a3
⑶
(y5)5
⑷
y5·y5
2.计算:
⑴
(x2)3·
(x2)2
⑵
(y3)4·
(y4)3
⑶
-(xn)2·
(x3)2m
⑷
(a2)3+a3
·
a3
随堂练习
思考题:
1、若
am
=
2,
则a3m
=_____.
2、若
mx
=
2,
my
=
3
,
则
mx+y
=___,
m3x+2y
=___.
8
6
72
动脑筋!
小结
相加
相乘
不变
不变
小结
Ⅰ.幂的乘方法则:
Ⅱ.特别注意同底数幂的乘法法则与幂的乘方的区别.
课堂作业:
课本P26页,习题6.2
第1、2
题.
6.2.1
幂的乘方
复习
幂的意义:
a·a·
…
·a
n个a
=an
同底数幂乘法的运算性质:
am
·
an
=am+n
(m,n都是正整数)
练习
木星
太阳
地球
(102)3=106,为什么?
体积扩大的倍数比半径扩大的倍数大得多.
地球、木星、太阳可以近似地看作球体
.木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的
倍和
倍
103
106
(102)3
=102×102×102
=102+2+2
=102×3
=106
太棒了!
(根据
)
(根据
).
同底数幂的乘法性质
幂的意义
如果这个正方体的棱长是
42
cm,那么它的体积是 cm3.
你知道
(42)3
是多少个
4
相乘吗
你知道吗?
(42)3
想一想:
幂的乘方,底数变不变?
指数应怎样计算?
试计算:
其中m
,
n都是正整数
(am)n
=am·am·
…
·am
n个am
=am+m+
…
+m
n个m
=amn
(幂的意义)
(同底数幂的乘法性质)
(乘法的意义)
幂的乘方法则:
其中m
,
n都是正整数
这就是说:
幂的乘方,底数不变,
指数相乘。
例1
计算:
解:
例1
计算:
解:
例2
计算:
解:原式=
解:原式=
例3
把
化成
的形式。
解:
想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
幂的乘方法则:
(其中m,n都是正整数)
同底数幂的乘法法则:
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m,n都是正整数
底数不变
口答:
⑴
(a2)4
⑵(b3m)4
⑶
(xn)m
⑷
(b3)3
⑸
x4·x4
⑹
(x4)7
口答:
⑻
(a3)3
⑽
(x6)5
⑺
-(y7)2
⑾
[(x+y)3]4
⑼
[(-1)3]5
⑿
[(a+1)3]n
1.计算:
要认真呀!
⑴
(a2)3
⑵
a2·a3
⑶
(y5)5
⑷
y5·y5
2.计算:
⑴
(x2)3·
(x2)2
⑵
(y3)4·
(y4)3
⑶
-(xn)2·
(x3)2m
⑷
(a2)3+a3
·
a3
随堂练习
思考题:
1、若
am
=
2,
则a3m
=_____.
2、若
mx
=
2,
my
=
3
,
则
mx+y
=___,
m3x+2y
=___.
8
6
72
动脑筋!
小结
相加
相乘
不变
不变
小结
Ⅰ.幂的乘方法则:
Ⅱ.特别注意同底数幂的乘法法则与幂的乘方的区别.
课堂作业:
课本P26页,习题6.2
第1、2
题.
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
