北师大版七年级数学下册 第2章 相交线与平行线单元复习卷(含答案)
文档属性
| 名称 | 北师大版七年级数学下册 第2章 相交线与平行线单元复习卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 150.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 15:13:15 | ||
图片预览


文档简介
第2章 相交线与平行线
一.选择题(共10小题)
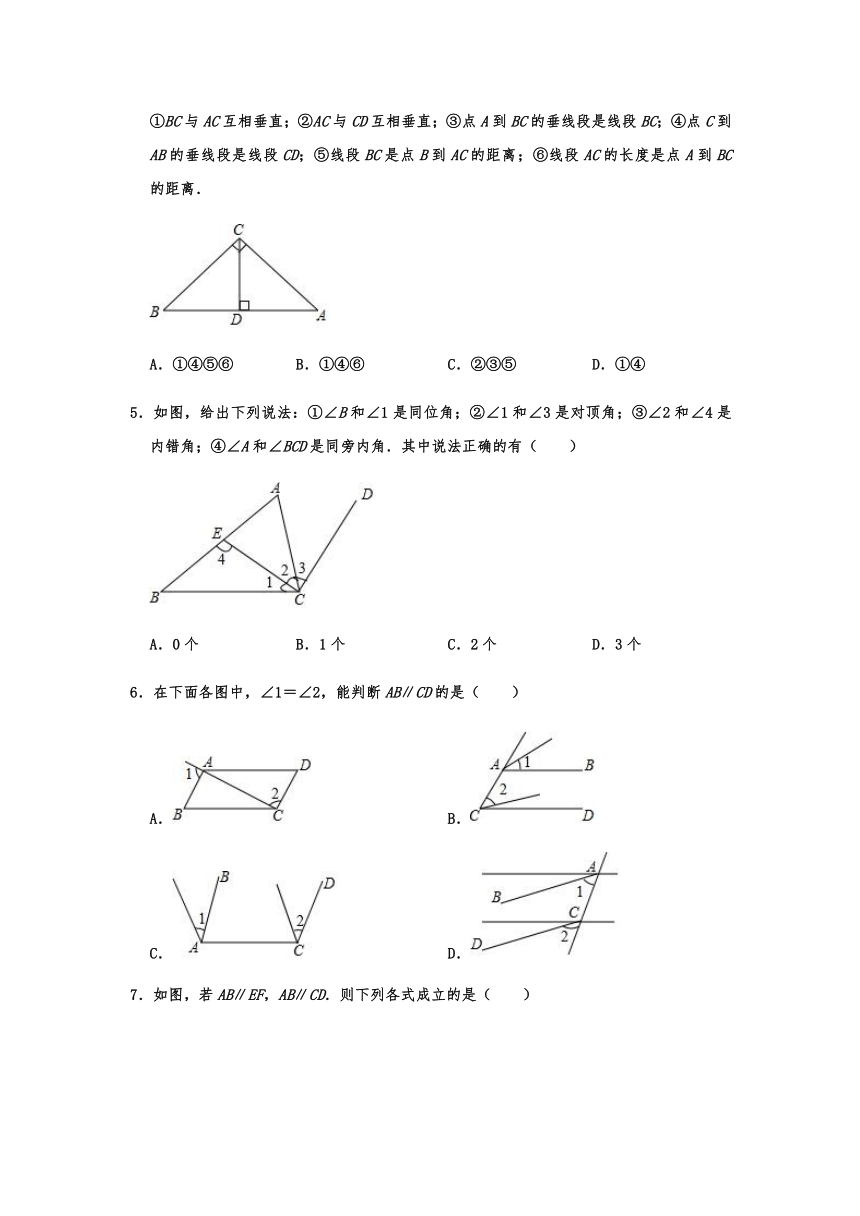
1.下列各图中,∠1和∠2是对顶角的是( )
A. B.
C. D.
2.同一平面内,∠A与∠B的两边互相垂直,∠B比∠A的2倍少30°,则∠A是( )
A.30° B.70° C.20°或110° D.30°或70°
3.小明参加跳远比赛,他从地面踏板P处起跳落到沙坑中,两脚后跟与沙坑的接触点分别为A,B,小明未站稳,一只手撑到沙坑C点,则跳远成绩测量正确的图是( )
A. B.
C. D.
4.如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中正确的是( )
①BC与AC互相垂直;②AC与CD互相垂直;③点A到BC的垂线段是线段BC;④点C到AB的垂线段是线段CD;⑤线段BC是点B到AC的距离;⑥线段AC的长度是点A到BC的距离.
A.①④⑤⑥ B.①④⑥ C.②③⑤ D.①④
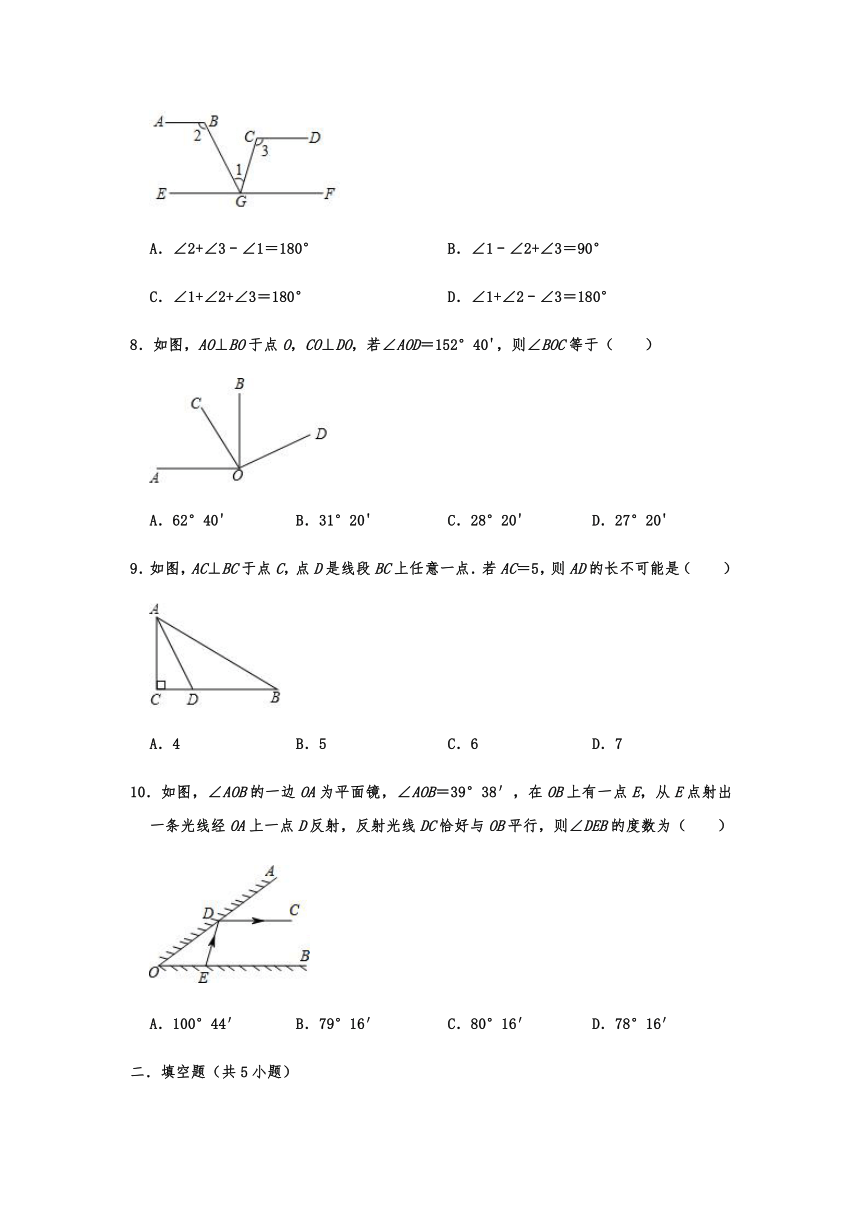
5.如图,给出下列说法:①∠B和∠1是同位角;②∠1和∠3是对顶角;③∠2和∠4是内错角;④∠A和∠BCD是同旁内角.其中说法正确的有( )
A.0个 B.1个 C.2个 D.3个
6.在下面各图中,∠1=∠2,能判断AB∥CD的是( )
A. B.
C. D.
7.如图,若AB∥EF,AB∥CD.则下列各式成立的是( )
A.∠2+∠3﹣∠1=180° B.∠1﹣∠2+∠3=90°
C.∠1+∠2+∠3=180° D.∠1+∠2﹣∠3=180°
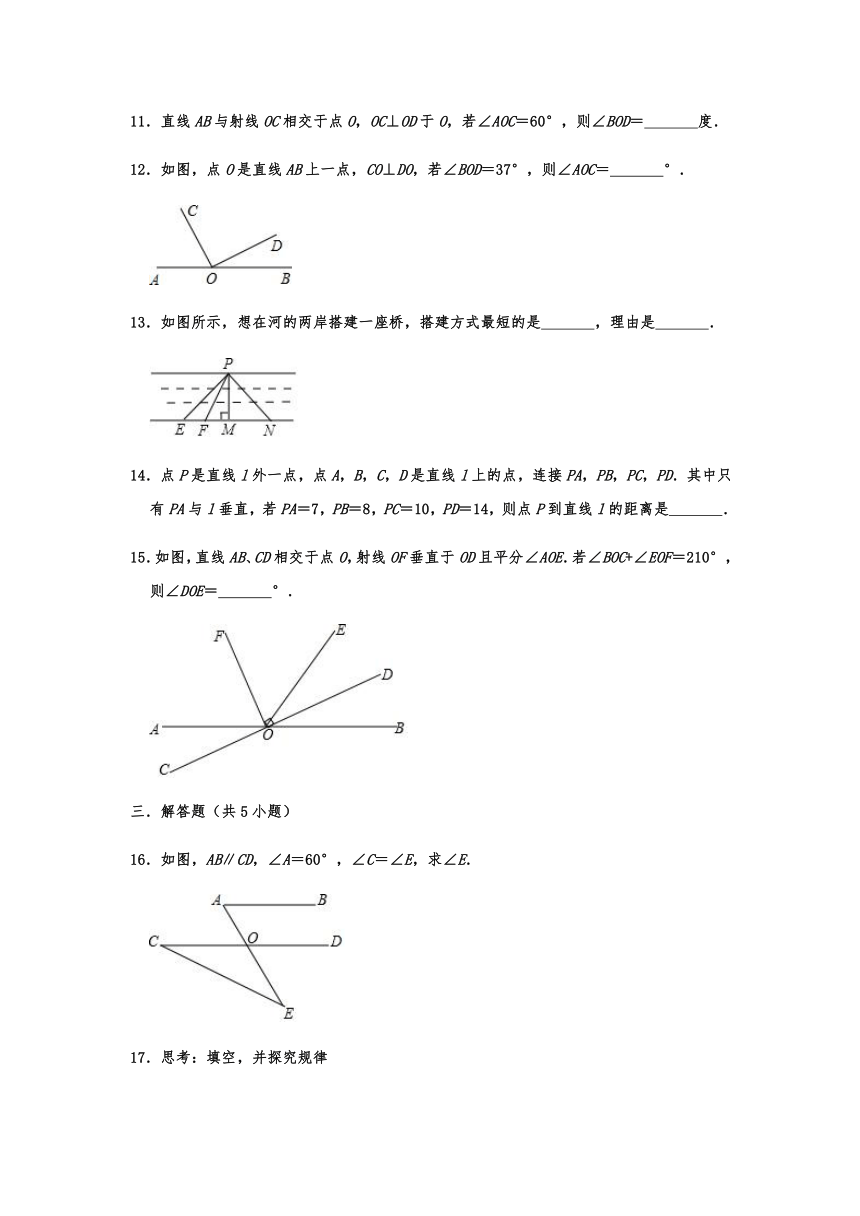
8.如图,AO⊥BO于点O,CO⊥DO,若∠AOD=152°40',则∠BOC等于( )
A.62°40' B.31°20' C.28°20' D.27°20'
9.如图,AC⊥BC于点C,点D是线段BC上任意一点.若AC=5,则AD的长不可能是( )
A.4 B.5 C.6 D.7
10.如图,∠AOB的一边OA为平面镜,∠AOB=39°38′,在OB上有一点E,从E点射出一条光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数为( )
A.100°44′ B.79°16′ C.80°16′ D.78°16′
二.填空题(共5小题)
11.直线AB与射线OC相交于点O,OC⊥OD于O,若∠AOC=60°,则∠BOD= 度.
12.如图,点O是直线AB上一点,CO⊥DO,若∠BOD=37°,则∠AOC= °.
13.如图所示,想在河的两岸搭建一座桥,搭建方式最短的是 ,理由是 .
14.点P是直线l外一点,点A,B,C,D是直线l上的点,连接PA,PB,PC,PD.其中只有PA与l垂直,若PA=7,PB=8,PC=10,PD=14,则点P到直线l的距离是 .
15.如图,直线AB、CD相交于点O,射线OF垂直于OD且平分∠AOE.若∠BOC+∠EOF=210°,则∠DOE= °.
三.解答题(共5小题)
16.如图,AB∥CD,∠A=60°,∠C=∠E,求∠E.
17.思考:填空,并探究规律
如图1,图2,OA∥EC,OB∥ED,∠AOB=30°,则图1中∠CED= °;图2中∠CED= °;用一句话概括你发现的规律
证明:请利用图1,图2证明你发现的规律;
应用:已知∠AOB=80°,∠CED=x°,OA∥CE,OB∥ED,则x的值为 (直接写出答案).
18.如图,直线a∥b,∠1=45°,∠2=30°,求∠P的度数.
19.如图,已知直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=36°.
(1)求∠AOG的度数;
(2)若OG是∠AOF的平分线,那么OC是∠AOE的平分线吗?说明你的理由.
20.将一副三角板中的两个直角顶点C叠放在一起(如图①),其中∠A=30°,∠B=60°,∠D=∠E=45°.
(1)猜想∠BCD与∠ACE的数量关系,并说明理由;
(2)若∠BCD=3∠ACE,求∠BCD的度数;
(3)若按住三角板ABC不动,绕顶点C转动三角板DCE,试探究∠BCD等于多少度时CE∥AB,并简要说明理由.
参考答案
一.选择题(共10小题)
1.
B.
2
D.
3.
D.
4.
B.
5.
B.
6.
D.
7.
A.
8.
D.
9.
A.
10.
B.
二.填空题(共5小题)
11.
150或30.
12.
53°.
13.
PM,垂线段最短.
14.
7.
15.
30.
三.解答题(共5小题)
16.解:∵AB∥CD,∠A=60°,
∴∠DOE=∠A=60°,
又∵∠C=∠E,∠DOE=∠C+∠E,
∴∠E=∠DOE=30°.
17.解:思考:∵OA∥EC,OB∥ED,∠AOB=30°
∴图1中∠CED=30°
∴图2中∠CED=150°
故可得到:两直线平行,同位角相等
应用:∵∠AOB=80°,OA∥CE,OB∥ED,
设∠CED=x°,
∴x的值为80或100.
故答案为:30,150,两直线平行,同位角相等,80或100.
18.解:
过P作PM∥直线a,
∵直线a∥b,
∴直线a∥b∥PM,
∵∠1=45°,∠2=30°,
∴∠EPM=∠2=30°,∠FPM=∠1=45°,
∴∠EPF=∠EPM+∠FPM=30°+45°=75°,
19.解:(1)∵AB、CD相交于点O,
∴∠AOC=∠BOD=36°,
∵OG⊥CD,
∴∠COG=90°,
即∠AOC+∠AOG=90°,
∴∠AOG=90°﹣∠AOC=90°﹣36o=54o;
(2)OC是∠AOE的平分线.理由
∵OG是∠AOF的角平分线,
∴∠AOG=∠GOF,
∵OG⊥CD,
∴∠COG=∠DOG=90°,
∴∠COA=∠DOF,
又∵∠DOF=∠COE,
∴∠AOC=∠COE,
∴OC平分∠AOE.
20.解:(1)∠BCD+∠ACE=180°,理由如下:
∵∠BCD=∠ACB+∠ACD=90°+∠ACD,
∴∠BCD+∠ACE=90°+∠ACD+∠ACE=90°+90°=180°;
(2)如图①,设∠ACE=α,则∠BCD=3α,
由(1)可得∠BCD+∠ACE=180°,
∴3α+α=180°,
∴α=45°,
∴∠BCD=3α=135°;
(3)分两种情况:
①如图1所示,当AB∥CE时,∠BCE=180°﹣∠B=120°,
又∵∠DCE=90°,
∴∠BCD=360°﹣120°﹣90°=150°;
②如图2所示,当AB∥CE时,∠BCE=∠B=60°,
又∵∠DCE=90°,
∴∠BCD=90°﹣60°=30°.
综上所述,∠BCD等于150°或30°时,CE∥AB.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
