华师大版八年级数学上册 13.5.3角平分线课件(20张PPT)
文档属性
| 名称 | 华师大版八年级数学上册 13.5.3角平分线课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 886.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 15:58:38 | ||
图片预览






文档简介
(共20张PPT)
角平分线
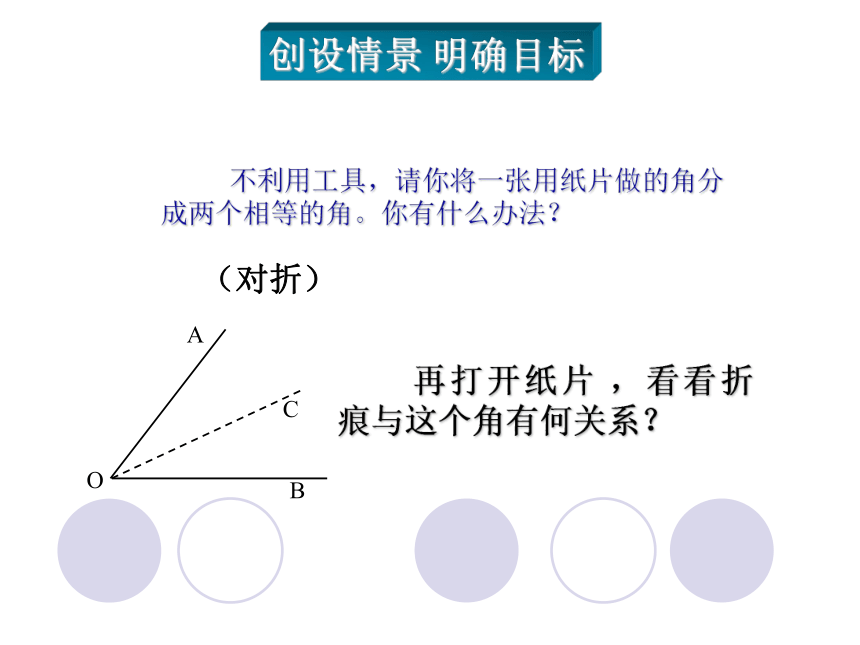
不利用工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?
A
O
B
C
再打开纸片 ,看看折痕与这个角有何关系?
(对折)
创设情景 明确目标
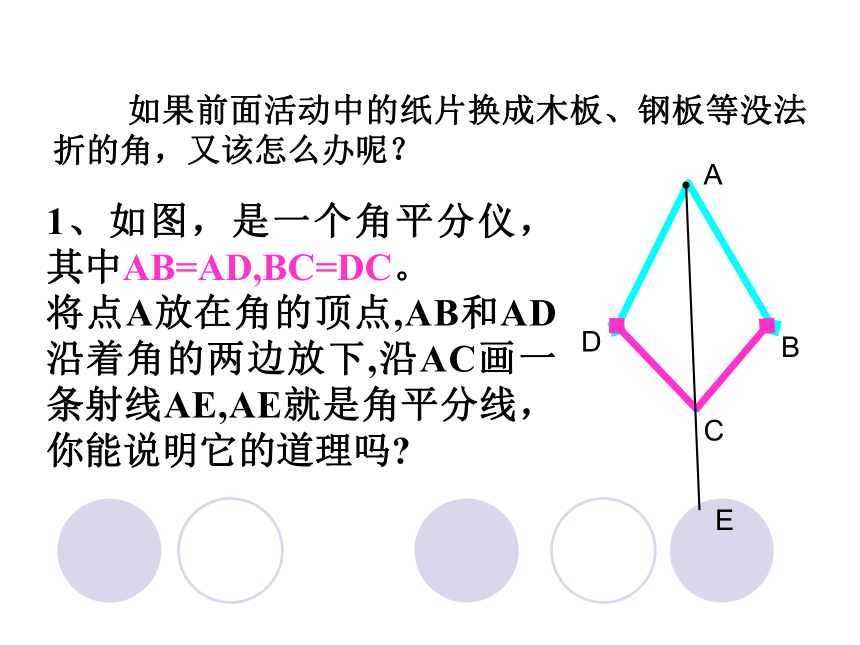
1、如图,是一个角平分仪,其中AB=AD,BC=DC。
将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗?
A
D
B
C
E
如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?
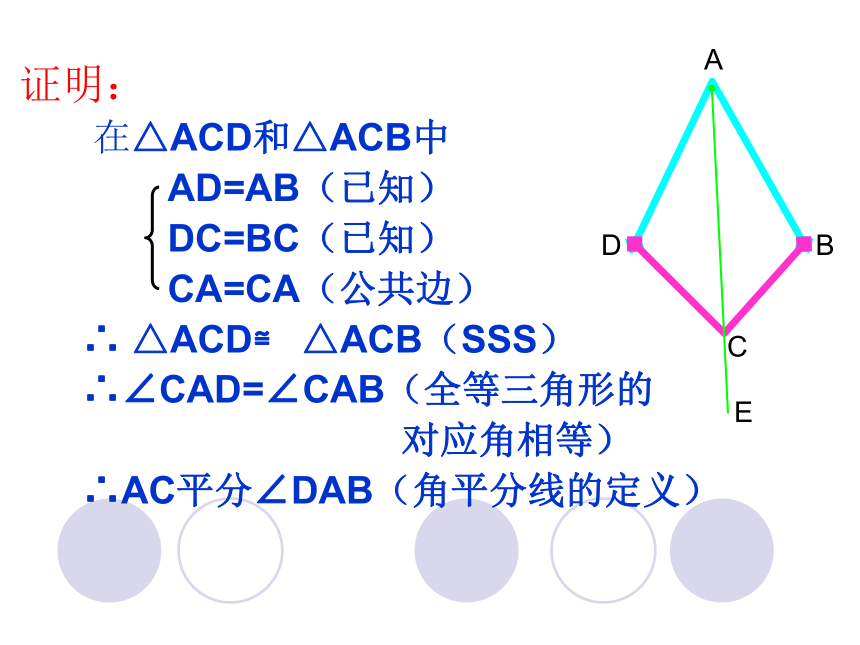
证明:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴ △ACD≌ △ACB(SSS)
∴∠CAD=∠CAB(全等三角形的
对应角相等)
∴AC平分∠DAB(角平分线的定义)
A
D
B
C
E
根据角平分仪的制作原理怎样作一个角的平分线?(不用角平分仪或量角器)
O
A
B
C
E
N
O
M
C
E
N
M
探究点一 角平分线的作法
1〉平分平角∠AOB
2〉通过上面的步骤,得到射线OC以后,把它反向延长得到直线CD,直线CD与直线AB是什么关系?
3〉结论:作平角的平分线即可平分平角,由此也得到过直线上一点作这条直线的垂线的方法。
A
B
O
C
D
知识产权代理合同范例_1
知识产权代理合同
知识产权代理合同
委托方(以下简称“甲方”)
受托方(以下简称“乙方”)
本合同由甲方与乙方在平等自愿的基础上,依据《中华人民共和国合同法》有关规定就甲方商标注册事宜,经双方友好协商后订立。
一、代理项目
甲方现委托乙方办理的如下事宜:
二、乙方义务
1、乙方须在收到甲方相关委托文件以及相应费用后3个工作日内做完所有前期准备并将相关文件转递申请,但涉及公证认证等无法控制的因素的除外。
2、乙方应保证按指定国家的主管机关要求提交申请材料,在代理过程中应及时将进展情况通知乙方。
3、乙方任何向官方所做的说明和回答,必须征得甲方同意。
4、如有涉及甲方同意进行并已经支付费用的后续程序,乙方应保证在指定国家的法律允许的期限内使当地事务所接到指令,但因甲方原因以及不可抗力造成的后果,乙方不承担责任。
三、甲方义务
1、甲方应及时向甲方提供申请所需文件资料,包含申请过程中可能出现的答复该国官方指令所需的文件资料;尽可能核实客户方文件的真实性、有效性,并确保送交乙方的文件准确无误;因原始文件缺陷造成的损失由甲方承担,但因乙方未审核出原始文件的应当可以发现的
探究点二 角平分线的性质
(1)实验:将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?
(2)猜想:角的平分线上的点到角的两边的距
离相等.
证明:∵OC平分∠ AOB (已知)
∴ ∠1= ∠2(角平分线的定义)
∵PD ⊥ OA,PE ⊥ OB(已知)
∴ ∠PDO= ∠PEO(垂直的定义)
在△PDO和△PEO中
∠PDO= ∠PEO(已证)
∠1= ∠2 (已证)
OP=OP (公共边)
∴ △PDO ≌ △PEO(AAS)
∴PD=PE(全等三角形的对应边相等)
P
A
O
B
C
E
D
1
2
已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于点D,PE⊥OB于点E
求证: PD=PE
(3)验证猜想
利用此性质怎样书写推理过程?
∵ ∠1= ∠2, PD ⊥ OA, PE ⊥ OB(已知)
∴PD=PE(全等三角形的对应边相等)
P
A
O
B
C
E
D
1
2
角平分线上的点到角两边的距离相等。
(4)得到角平分线的性质
探究点三 角的平分线的性质的运用
例 如图,△ABC 的角平分线BM,CN 相交于点
P.求证:点P到三边AB,BC,CA 的距离相等.
A
B
C
P
M
N
证明: ∵ QD⊥OA,QE⊥OB(已知),
∴ ∠QDO=∠QEO=90°(垂直的定义)
在Rt△QDO和Rt△QEO中
QO=QO(公共边)
QD=QE
∴ Rt△QDO≌Rt△QEO(HL)
∴ ∠QOD=∠QOE
∴点Q在∠AOB的平分线上
已知:如图,QD⊥OA,QE⊥OB,点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
探究点四 角平分线的判定
到角的两边的距离相等的点在角的平分线上。
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
用数学语言表示为:
角的平分线上的点到角的两边的距离相等.
归纳
1.如图, △ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB、BC、CA的距离相等
∵BM是△ABC的角平分线,点P在BM上,
A
B
C
P
M
N
D
E
F
∴PD=PE
(角平分线上的点到这个角的两边距离相等).
同理,PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等
证明:过点P作PD⊥AB于D, PE⊥BC于E,PF⊥AC于F
练一练
2.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
证明:
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M
G
H
M
∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC
∴FG=FM
又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC
∴FM=FH
∴FG=FH
∴点F在∠DAE的平分线上
2.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
证明:
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M
G
H
M
∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC
∴FG=FM
又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC
∴FM=FH
∴FG=FH
∴点F在∠DAE的平分线上
(1)本节课学习了哪些主要内容?
(2)本节课是通过什么方式探究角的平分线的性质的?
(3)角的平分线的性质为我们提供了证明什么的方法?
在应用这一性质时要注意哪些问题?
总结梳理 内化目标
练习1 下列结论一定成立的是 .
(2)如图,点P 在OC 上,PD⊥OA,PE⊥OB,垂足
分别为D,E,则PD =PE.
A
B
O
P
C
D
E
达标检测 反思目标
练习1 下列结论一定成立的是 .
(3)如图,OC 平分∠AOB,点P 在OC 上,PD⊥OA,
垂足为D.若PD =3,则点P 到OB 的距离为3.
(3)
A
B
O
P
C
D
在此题的已知条件下,
你还能得到哪些结论?
练习2 如图,△ABC中,∠B =∠C,AD 是∠BAC
的平分线, DE⊥AB,DF⊥AC,垂足分别为E,F.求
证:EB =FC.
A
B
C
D
E
F
课后作业:教材同步习题.
课后作业
角平分线
不利用工具,请你将一张用纸片做的角分成两个相等的角。你有什么办法?
A
O
B
C
再打开纸片 ,看看折痕与这个角有何关系?
(对折)
创设情景 明确目标
1、如图,是一个角平分仪,其中AB=AD,BC=DC。
将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是角平分线,你能说明它的道理吗?
A
D
B
C
E
如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?
证明:
在△ACD和△ACB中
AD=AB(已知)
DC=BC(已知)
CA=CA(公共边)
∴ △ACD≌ △ACB(SSS)
∴∠CAD=∠CAB(全等三角形的
对应角相等)
∴AC平分∠DAB(角平分线的定义)
A
D
B
C
E
根据角平分仪的制作原理怎样作一个角的平分线?(不用角平分仪或量角器)
O
A
B
C
E
N
O
M
C
E
N
M
探究点一 角平分线的作法
1〉平分平角∠AOB
2〉通过上面的步骤,得到射线OC以后,把它反向延长得到直线CD,直线CD与直线AB是什么关系?
3〉结论:作平角的平分线即可平分平角,由此也得到过直线上一点作这条直线的垂线的方法。
A
B
O
C
D
知识产权代理合同范例_1
知识产权代理合同
知识产权代理合同
委托方(以下简称“甲方”)
受托方(以下简称“乙方”)
本合同由甲方与乙方在平等自愿的基础上,依据《中华人民共和国合同法》有关规定就甲方商标注册事宜,经双方友好协商后订立。
一、代理项目
甲方现委托乙方办理的如下事宜:
二、乙方义务
1、乙方须在收到甲方相关委托文件以及相应费用后3个工作日内做完所有前期准备并将相关文件转递申请,但涉及公证认证等无法控制的因素的除外。
2、乙方应保证按指定国家的主管机关要求提交申请材料,在代理过程中应及时将进展情况通知乙方。
3、乙方任何向官方所做的说明和回答,必须征得甲方同意。
4、如有涉及甲方同意进行并已经支付费用的后续程序,乙方应保证在指定国家的法律允许的期限内使当地事务所接到指令,但因甲方原因以及不可抗力造成的后果,乙方不承担责任。
三、甲方义务
1、甲方应及时向甲方提供申请所需文件资料,包含申请过程中可能出现的答复该国官方指令所需的文件资料;尽可能核实客户方文件的真实性、有效性,并确保送交乙方的文件准确无误;因原始文件缺陷造成的损失由甲方承担,但因乙方未审核出原始文件的应当可以发现的
探究点二 角平分线的性质
(1)实验:将∠AOB对折,再折出一个直角三角形(使第一条折痕为斜边),然后展开,观察两次折叠形成的三条折痕,你能得出什么结论?
(2)猜想:角的平分线上的点到角的两边的距
离相等.
证明:∵OC平分∠ AOB (已知)
∴ ∠1= ∠2(角平分线的定义)
∵PD ⊥ OA,PE ⊥ OB(已知)
∴ ∠PDO= ∠PEO(垂直的定义)
在△PDO和△PEO中
∠PDO= ∠PEO(已证)
∠1= ∠2 (已证)
OP=OP (公共边)
∴ △PDO ≌ △PEO(AAS)
∴PD=PE(全等三角形的对应边相等)
P
A
O
B
C
E
D
1
2
已知:如图,OC平分∠AOB,点P在OC上,PD⊥OA于点D,PE⊥OB于点E
求证: PD=PE
(3)验证猜想
利用此性质怎样书写推理过程?
∵ ∠1= ∠2, PD ⊥ OA, PE ⊥ OB(已知)
∴PD=PE(全等三角形的对应边相等)
P
A
O
B
C
E
D
1
2
角平分线上的点到角两边的距离相等。
(4)得到角平分线的性质
探究点三 角的平分线的性质的运用
例 如图,△ABC 的角平分线BM,CN 相交于点
P.求证:点P到三边AB,BC,CA 的距离相等.
A
B
C
P
M
N
证明: ∵ QD⊥OA,QE⊥OB(已知),
∴ ∠QDO=∠QEO=90°(垂直的定义)
在Rt△QDO和Rt△QEO中
QO=QO(公共边)
QD=QE
∴ Rt△QDO≌Rt△QEO(HL)
∴ ∠QOD=∠QOE
∴点Q在∠AOB的平分线上
已知:如图,QD⊥OA,QE⊥OB,点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
探究点四 角平分线的判定
到角的两边的距离相等的点在角的平分线上。
∵ QD⊥OA,QE⊥OB,QD=QE.
∴点Q在∠AOB的平分线上.
用数学语言表示为:
角的平分线上的点到角的两边的距离相等.
归纳
1.如图, △ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB、BC、CA的距离相等
∵BM是△ABC的角平分线,点P在BM上,
A
B
C
P
M
N
D
E
F
∴PD=PE
(角平分线上的点到这个角的两边距离相等).
同理,PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等
证明:过点P作PD⊥AB于D, PE⊥BC于E,PF⊥AC于F
练一练
2.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
证明:
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M
G
H
M
∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC
∴FG=FM
又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC
∴FM=FH
∴FG=FH
∴点F在∠DAE的平分线上
2.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
证明:
过点F作FG⊥AE于G,FH⊥AD于H,FM⊥BC于M
G
H
M
∵点F在∠BCE的平分线上, FG⊥AE, FM⊥BC
∴FG=FM
又∵点F在∠CBD的平分线上, FH⊥AD, FM⊥BC
∴FM=FH
∴FG=FH
∴点F在∠DAE的平分线上
(1)本节课学习了哪些主要内容?
(2)本节课是通过什么方式探究角的平分线的性质的?
(3)角的平分线的性质为我们提供了证明什么的方法?
在应用这一性质时要注意哪些问题?
总结梳理 内化目标
练习1 下列结论一定成立的是 .
(2)如图,点P 在OC 上,PD⊥OA,PE⊥OB,垂足
分别为D,E,则PD =PE.
A
B
O
P
C
D
E
达标检测 反思目标
练习1 下列结论一定成立的是 .
(3)如图,OC 平分∠AOB,点P 在OC 上,PD⊥OA,
垂足为D.若PD =3,则点P 到OB 的距离为3.
(3)
A
B
O
P
C
D
在此题的已知条件下,
你还能得到哪些结论?
练习2 如图,△ABC中,∠B =∠C,AD 是∠BAC
的平分线, DE⊥AB,DF⊥AC,垂足分别为E,F.求
证:EB =FC.
A
B
C
D
E
F
课后作业:教材同步习题.
课后作业
