沪科版数学七年级下册课件:7.2.3 一元一次不等式的应用(20张PPT)
文档属性
| 名称 | 沪科版数学七年级下册课件:7.2.3 一元一次不等式的应用(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-05 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
第3课时 一元一次不等式的应用
上节课我们学习了如何解一元一次不等式,这节课我们学习如何列一元一次不等式解决简单的实际问题.
例3 松山公园菊花展个人票每张 10 元,20 人以上(含 20 人)的团体票 8 折优惠. 在人数不足 20 人的情况下,试问何时买 20 人的团体票比买个人票要便宜?
解 设人数为 x,买个人票需要 10x 元,买 20 人的团体票需要 20×10×80%元,根据题意,得
10x > 20×10×80%.
解不等式,得 x > 16.
因为人数必须是小于 20 的整数,即 x <20. 因此,当人数是 17,18,19 时,买 20 人的团体票比买个人票要便宜.
在“科学与艺术”知识竞赛的预选赛中共有20 道题,对于每一道题,答对得 10 分,答错或不答扣 5 分,总得分不少于 80 分者通过预选赛.育才中学有 25 名学生通过了预选赛,通过者至少答对了多少道题?有哪些可能的情形.
练习
解:设通过者答对了 x 道题,答错或不答的题有(20 – x)道,根据题意可得,
10x – 5(20 – x)≥ 80
解得:x ≥12
所以,通过者至少要答对 12 道题.
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买 100 元后,超出 100 元的部分按 90% 收费;在乙商场累计购买超过 50 元后,超过 50 元的部分按 95% 收费. 顾客到哪家商场购物花费少?
分析
在甲商场购物超过 100 元后享受优惠,在乙商场购物超过 50 元后享受优惠.因此,我们需要分三种情况讨论:
(1)累计购物不超过 50 元;
(2)累计购物超过 50 元而不超过 100 元;
(3)累计购物超过 100 元.
x
x
x
100+0.9(x-100)
50+0.95(x-50)
50+0.95(x-50)
购物款 在甲商场花费 在乙商场花费
不超过50元
(0<x≤50)
超过50,但不超过100元
(50<x≤100)
超过100元
(x>100)
(a)当 0 < x ≤ 50 时,在两家商场花费一样,因为都不享受优惠.
(b)当 50 < x ≤ 100 时,在乙商场花费少,因为乙商场有优惠,甲商场没有.
若在乙商场花费少,则有不等式:
50 + 0.95(x – 150)< 100 + 0.9(x – 100),
解得 x < 150.
(c)当 x > 100 时,若在甲商场花费少,则有不等式:
50 + 0.95(x – 50)> 100 + 0.9(x – 100),
解得 x > 150.
购物不超过 50 元和刚好是 150 元时,在两家商场购物,花费没有区别.
购物款 在甲商
场花费 在乙商
场花费 比较
0 < x ≤ 50 x x 一样
50 < x ≤ 100
x 50 + 0.95
(x – 50) 在乙商场少
x>100 100<x<150 100 + 0.9
(x – 100) 50 + 0.95
(x – 50) 在乙商场少
x=150 一样
x>150 在甲商场少
购物超过 50 元而不到 150 元时,在乙商场购物花费少.
购物款 在甲商
场花费 在乙商
场花费 比较
0 < x ≤ 50 x x 一样
50 < x ≤ 100 x 50 + 0.95
(x – 50) 在乙商场少
x>100 100<x<150 100 + 0.9
(x – 100) 50 + 0.95
(x – 50) 在乙商场少
x=150 一样
x>150 在甲商场少
超过 150 元后,在甲商场购物花费少.
购物款 在甲商
场花费 在乙商
场花费 比较
0 < x ≤ 50 x x 一样
50 < x ≤ 100
x 50 + 0.95
(x – 50) 在乙商场少
x>100 100<x<150 100 + 0.9
(x – 100) 50 + 0.95
(x – 50) 在乙商场少
x=150 一样
x>150 在甲商场少
1. 毛笔每支2 元,钢笔每支 5 元,现有的购买费用不足 20 元,则购买毛笔和钢笔允许的情况是( )
A. 5支毛笔,2 支钢笔
B. 4支毛笔,3 支钢笔
C. 0支毛笔,5 支钢笔
D. 7支毛笔,1 支钢笔
D
2. 某种商品的进价为 800 元,出售时标价为1200 元,后来由于该商品积压,商店准备打折出售,但要保持利润率不低于进价 5%,则至多可打( )
A. 6折 B. 7折
C. 8折 D. 9折
B
3. 某工人计划在 15 天内加工 408 个零件,最初三天中每天加工 24 个.问以后每天至少加工多少个零件,才能在规定的时间内超额完成任务?
解:设后面每天加工 x 个零件,则
24×3 +(15 – 3)x > 408
12x > 336,
x > 28,
那么每天加工的个数应大于 28 个,才能超额完成任务.
4. 某工厂前年有员工 280 人,去年经过结构改革减员 40 人,全厂年利润增加 100 万元,人均创利至少增加 6000 元,前年全厂利润至少是多少?
答:前年全厂利润至少是 308 万元.
第3课时 一元一次不等式的应用
上节课我们学习了如何解一元一次不等式,这节课我们学习如何列一元一次不等式解决简单的实际问题.
例3 松山公园菊花展个人票每张 10 元,20 人以上(含 20 人)的团体票 8 折优惠. 在人数不足 20 人的情况下,试问何时买 20 人的团体票比买个人票要便宜?
解 设人数为 x,买个人票需要 10x 元,买 20 人的团体票需要 20×10×80%元,根据题意,得
10x > 20×10×80%.
解不等式,得 x > 16.
因为人数必须是小于 20 的整数,即 x <20. 因此,当人数是 17,18,19 时,买 20 人的团体票比买个人票要便宜.
在“科学与艺术”知识竞赛的预选赛中共有20 道题,对于每一道题,答对得 10 分,答错或不答扣 5 分,总得分不少于 80 分者通过预选赛.育才中学有 25 名学生通过了预选赛,通过者至少答对了多少道题?有哪些可能的情形.
练习
解:设通过者答对了 x 道题,答错或不答的题有(20 – x)道,根据题意可得,
10x – 5(20 – x)≥ 80
解得:x ≥12
所以,通过者至少要答对 12 道题.
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买 100 元后,超出 100 元的部分按 90% 收费;在乙商场累计购买超过 50 元后,超过 50 元的部分按 95% 收费. 顾客到哪家商场购物花费少?
分析
在甲商场购物超过 100 元后享受优惠,在乙商场购物超过 50 元后享受优惠.因此,我们需要分三种情况讨论:
(1)累计购物不超过 50 元;
(2)累计购物超过 50 元而不超过 100 元;
(3)累计购物超过 100 元.
x
x
x
100+0.9(x-100)
50+0.95(x-50)
50+0.95(x-50)
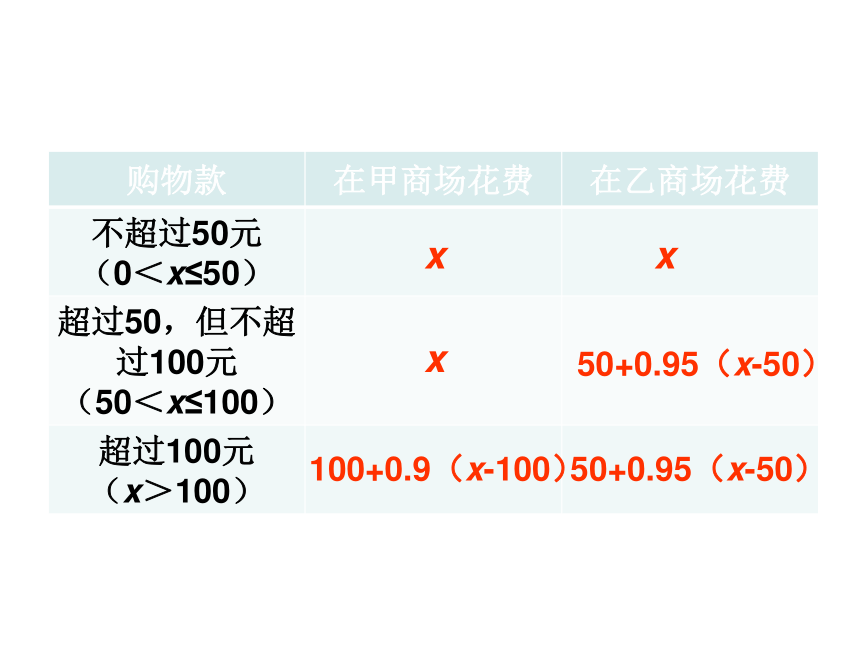
购物款 在甲商场花费 在乙商场花费
不超过50元
(0<x≤50)
超过50,但不超过100元
(50<x≤100)
超过100元
(x>100)
(a)当 0 < x ≤ 50 时,在两家商场花费一样,因为都不享受优惠.
(b)当 50 < x ≤ 100 时,在乙商场花费少,因为乙商场有优惠,甲商场没有.
若在乙商场花费少,则有不等式:
50 + 0.95(x – 150)< 100 + 0.9(x – 100),
解得 x < 150.
(c)当 x > 100 时,若在甲商场花费少,则有不等式:
50 + 0.95(x – 50)> 100 + 0.9(x – 100),
解得 x > 150.
购物不超过 50 元和刚好是 150 元时,在两家商场购物,花费没有区别.
购物款 在甲商
场花费 在乙商
场花费 比较
0 < x ≤ 50 x x 一样
50 < x ≤ 100
x 50 + 0.95
(x – 50) 在乙商场少
x>100 100<x<150 100 + 0.9
(x – 100) 50 + 0.95
(x – 50) 在乙商场少
x=150 一样
x>150 在甲商场少
购物超过 50 元而不到 150 元时,在乙商场购物花费少.
购物款 在甲商
场花费 在乙商
场花费 比较
0 < x ≤ 50 x x 一样
50 < x ≤ 100 x 50 + 0.95
(x – 50) 在乙商场少
x>100 100<x<150 100 + 0.9
(x – 100) 50 + 0.95
(x – 50) 在乙商场少
x=150 一样
x>150 在甲商场少
超过 150 元后,在甲商场购物花费少.
购物款 在甲商
场花费 在乙商
场花费 比较
0 < x ≤ 50 x x 一样
50 < x ≤ 100
x 50 + 0.95
(x – 50) 在乙商场少
x>100 100<x<150 100 + 0.9
(x – 100) 50 + 0.95
(x – 50) 在乙商场少
x=150 一样
x>150 在甲商场少
1. 毛笔每支2 元,钢笔每支 5 元,现有的购买费用不足 20 元,则购买毛笔和钢笔允许的情况是( )
A. 5支毛笔,2 支钢笔
B. 4支毛笔,3 支钢笔
C. 0支毛笔,5 支钢笔
D. 7支毛笔,1 支钢笔
D
2. 某种商品的进价为 800 元,出售时标价为1200 元,后来由于该商品积压,商店准备打折出售,但要保持利润率不低于进价 5%,则至多可打( )
A. 6折 B. 7折
C. 8折 D. 9折
B
3. 某工人计划在 15 天内加工 408 个零件,最初三天中每天加工 24 个.问以后每天至少加工多少个零件,才能在规定的时间内超额完成任务?
解:设后面每天加工 x 个零件,则
24×3 +(15 – 3)x > 408
12x > 336,
x > 28,
那么每天加工的个数应大于 28 个,才能超额完成任务.
4. 某工厂前年有员工 280 人,去年经过结构改革减员 40 人,全厂年利润增加 100 万元,人均创利至少增加 6000 元,前年全厂利润至少是多少?
答:前年全厂利润至少是 308 万元.
