人教版九年级数学下册27.2.1相似三角形的判定课件(第1课时 共34张PPT)
文档属性
| 名称 | 人教版九年级数学下册27.2.1相似三角形的判定课件(第1课时 共34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 677.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 17:17:12 | ||
图片预览




文档简介
(共34张PPT)
27.2.1相似三角形的判定
第1课时
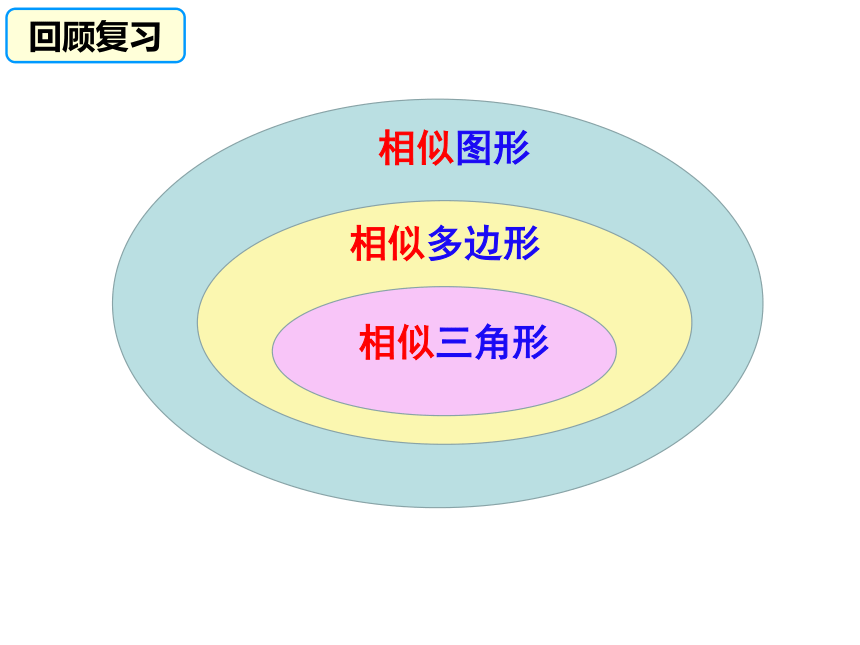
1.相似图形的定义:
我们把这些形状相同的图形,叫做相似图形。
回顾复习
2.(1)相似多边形的定义:
两个边数相同的多边形,如果它们的角分别
相等,边成比例,那么这两个多边形叫相似多边形。
(2)相似多边形的性质:
相似多边形的对应角相等,对应边成比例.
回顾复习
相似图形
相似多边形
相似三角形
§27.2.1
的判定
1.了解相似三角形的概念及表示方法。
2.理解并掌握平行线分线段成比例定理及平行于三角形一边的直线的性质定理【重点、难点】
学习目标
第一课时
平行线分线段成比例定理
相似三角形
_________________________
新知探究1
相似三角形的概念
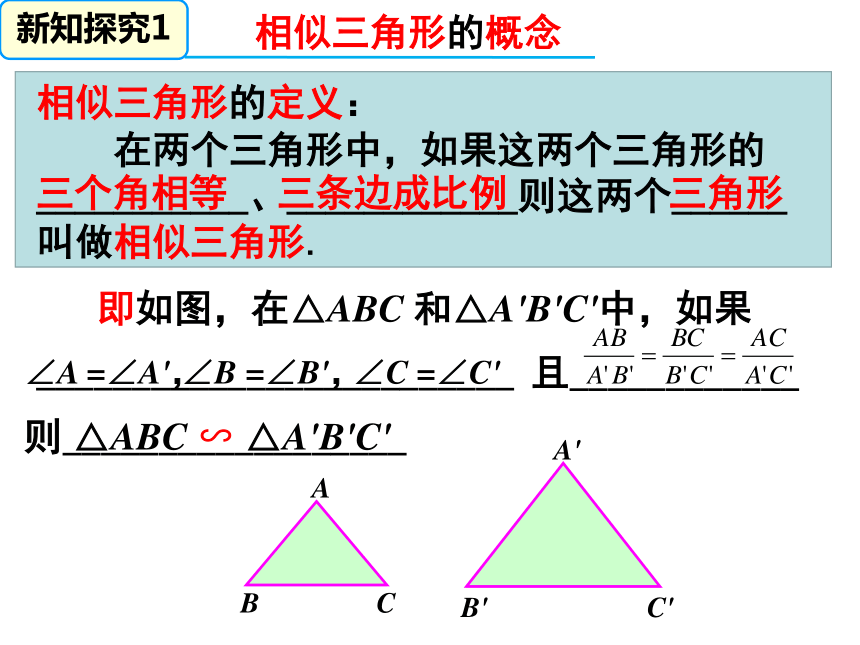
相似三角形的定义:
在两个三角形中,如果这两个三角形的___________、____________则这两个______
叫做相似三角形.
三个角相等
三条边成比例
三角形
即如图,在△ABC
和△A'B'C'中,如果
∠A
=∠A',
∠B
=∠B',
∠C
=∠C'
A
B
C
A'
B'
C'
则__________________
且____________
△ABC
∽
△A'B'C'
A
B
C
A'
B'
C'
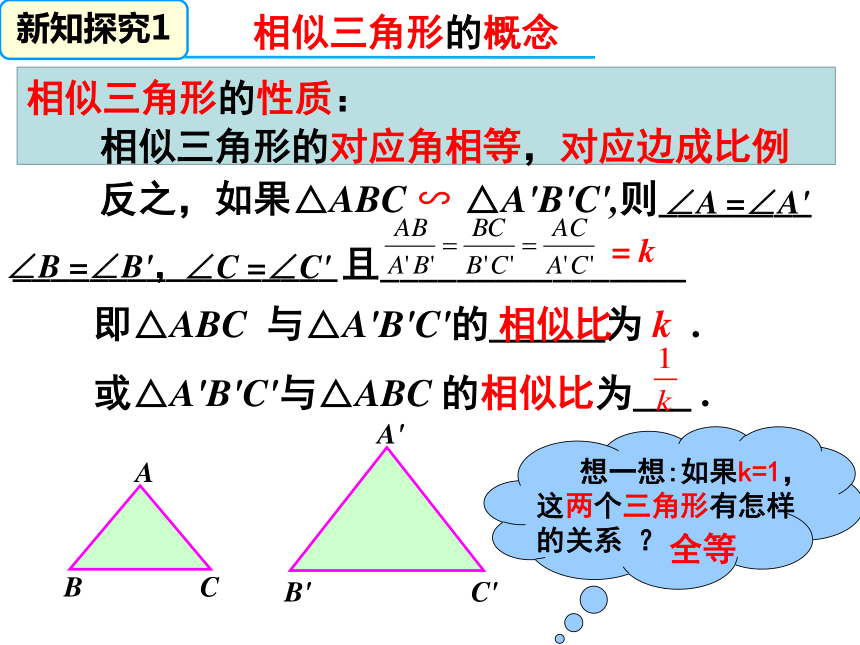
反之,如果△ABC
∽
△A'B'C',则________
∠A
=∠A'
∠B
=∠B',
∠C
=∠C'
_________________
=
k
即△ABC
与△A'B'C'的______为
k
.
或△A'B'C'与△ABC
的相似比为___
.
相似比
想一想:如果k=1,这两个三角形有怎样的关系
?
新知探究1
相似三角形的概念
相似三角形的性质:
相似三角形的对应角相等,对应边成比例
且________________
全等
小结归纳1
1.相似三角形的定义:
在两个三角形中,如果这两个三角形的三
个角相等,三条边成比例则两个三角形叫做相似三角形。
学习目标
1.了解相似三角形的概念及表示方法。
2.相似三角形的性质:
相似三角形的对应角相等,对应边成比例
新知探究2
相似三角形的判定
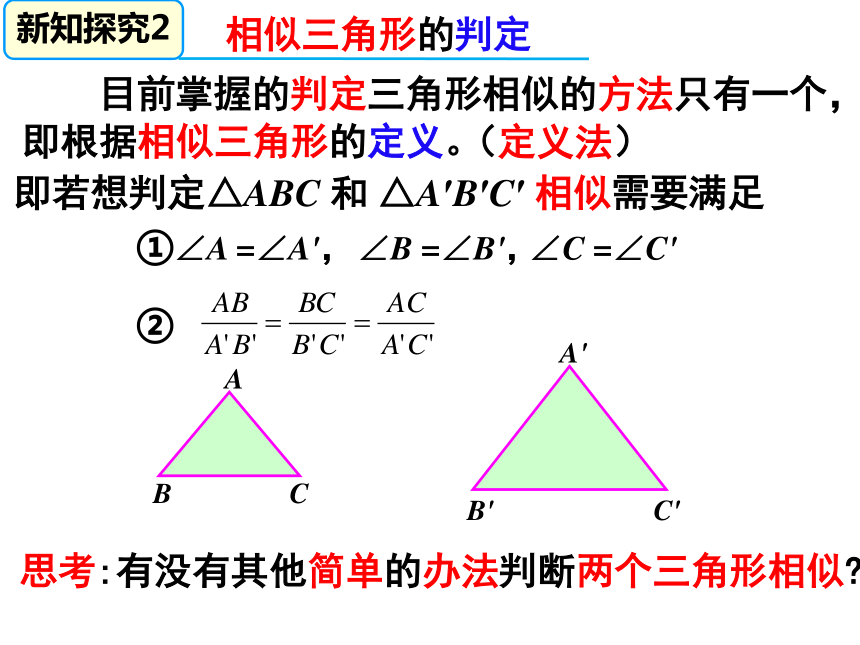
思考:有没有其他简单的办法判断两个三角形相似
∠A
=∠A',
∠B
=∠B',
∠C
=∠C'
①
A
B
C
A'
B'
C'
②
目前掌握的判定三角形相似的方法只有一个,即根据相似三角形的定义。
(定义法)
即若想判定△ABC
和
△A′B′C′
相似需要满足
在△ABC中,
DE∥BC
A
B
C
D
E
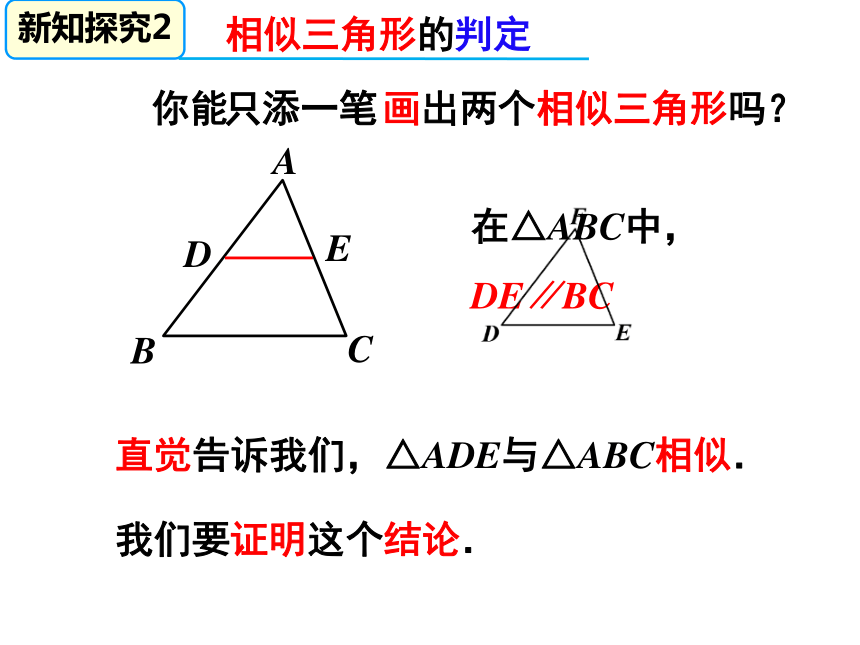
我们要证明这个结论.
你能
画出两个相似三角形吗?
直觉告诉我们,△ADE与△ABC相似.
只添一笔
新知探究2
相似三角形的判定
A
B
C
D
E
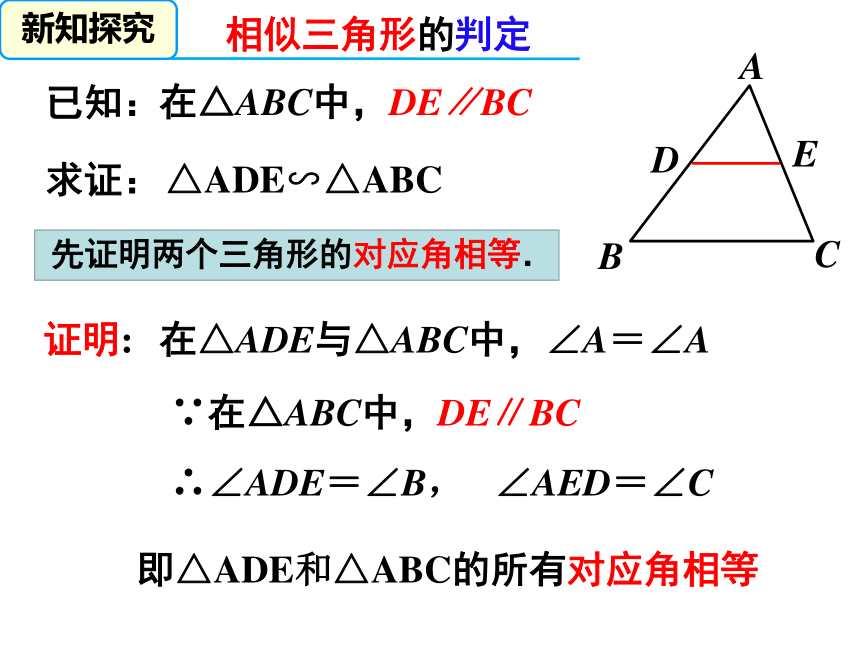
在△ABC中,DE∥BC
△ADE∽△ABC
先证明两个三角形的对应角相等.
∵在△ABC中,DE∥BC
∴∠ADE=∠B,
∠AED=∠C
即△ADE和△ABC的所有对应角相等
证明:
在△ADE与△ABC中,∠A=∠A
已知:
求证:
新知探究
相似三角形的判定
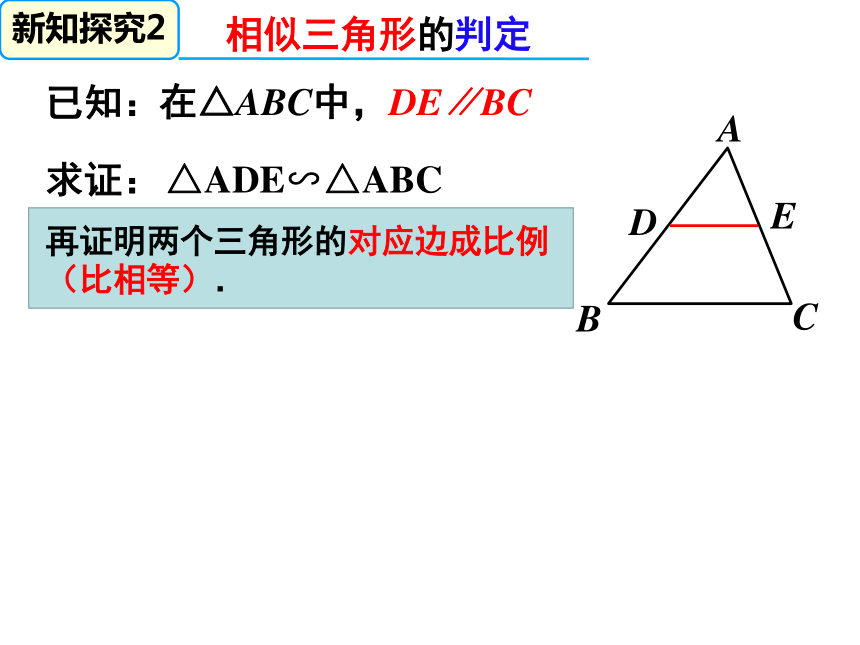
再证明两个三角形的对应边成比例(比相等).
A
B
C
D
E
在△ABC中,DE∥BC
△ADE∽△ABC
已知:
求证:
新知探究2
相似三角形的判定
(
)
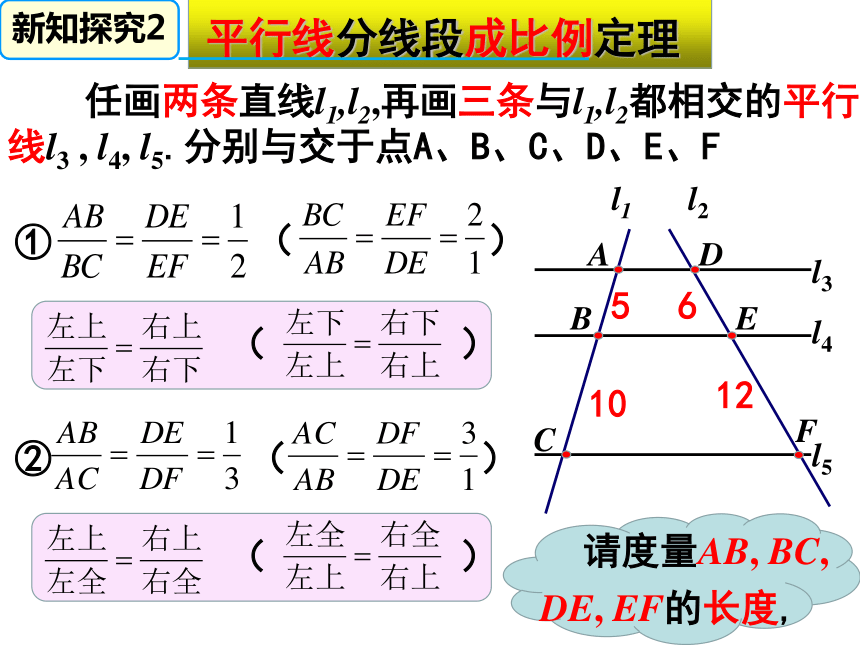
平行线分线段成比例定理
任画两条直线l1,l2,再画三条与l1,l2都相交的平行
线l3
,
l4,
l5.分别与交于点A、B、C、D、E、F
DE,
EF的长度,
新知探究2
A
B
C
D
E
F
l3
l4
l5
l1
l2
请度量AB,
BC,
5
6
10
12
①
(
)
(
)
②
(
)
(
)
任画两条直线l1,l2,再画三条与l1,l2都相交的平行
线l3
,
l4,
l5.分别与交于点A、B、C、D、E、F
DE,
EF的长度,
新知探究2
A
B
C
D
E
F
l3
l4
l5
l1
l2
请度量AB,
BC,
5
6
10
12
(
)
③
平行线分线段成比例定理
任画两条直线l1,l2,再画三条与l1,l2都相交的平行
线l3
,
l4,
l5.分别与交于点A、B、C、D、E、F
(
)
(
)
(
)
①
③
②
?
?
?
?
?
?
新知探究2
A
B
C
D
E
F
l3
l4
l5
l1
l2
5
6
10
12
DE,
EF的长度,
请度量AB,
BC,
新知探究2
平行线分线段成比例定理
利用等积法证明平行线分线段成比例定理。
线段成比例。
平行线分线段成比例定理:
一组
三条
只要
就有
l3
//l4
//
l5
∴
∵
或
或
两条直线
被
平行线所截,
所得的对应
符号语言:
小结归纳2
…
A
B
C
l4
l5
l1
D
E
F
l2
l3
A(D)
B
C
E
F
把直线l2向左或向右任意平移,
这些线段依然成比例.
(使D与A重合)
把此图形抽取出来。
新知探究3
平行于三角形一边的直线的性质定理
图中有哪些成比例的线段?
A
B
C
E
F
新知探究3
平行于三角形一边的直线的性质定理
A
B
C
l4
l5
l1
D
E
F
l2
l3
A
B
C
(E)
F
D
(使B和E重合)
把直线l2向左或向右任意平移,
这些线段依然成比例.
把此图形抽取出来。
新知探究3
平行于三角形一边的直线的性质定理
图中有哪些成比例的线段?
A
B
C
F
D
新知探究3
平行于三角形一边的直线的性质定理
边的延长线),所得的
平行线分线段成比例定理的推论:
A
B
C
E
F
A
B
C
F
D
对应线段成比例.
平行于
三角形一边的直线
截其他两边
(或两
在三角形中只要具备平行条件就可以直接得到对应线段成比例
新知探究3
平行于三角形一边的直线的性质定理:
平行于三角形一边的直线的性质定理
“A
”型
“X
”型
小结归纳3
平行于三角形一边的直线的性质定理
在△ABC中,DE∥BC,
∴
∵
符号语言:(以“A”型为例)
边的延长线),所得的
对应线段成比例.
平行于
三角形一边的直线
截其他两边
(或两
…
平行线分线段成比例定理:
两条直线被一组______所截,所得的对应线段______
平行线
成比例
平行于三角形一边的直线的性质定理:
平行于三角形一边的直线截其他两边(或两边延长线),所得的______线段______.
对应
成比例
小结
1.已知l1∥l2∥l3,下列比例式中错误的是(
)
A.
B.
C.
D.
D
基础训练1
A
C
E
B
D
F
l2
l1
l3
平行线分线段成比例定理
2.已知梯形ABCD中,
AD∥BC,EF∥BC,AE=FC,
,
,求:AE的长.
∴AE=6.
练一练
变式训练1
平行线分线段成比例定理
A
E
C
D
F
B
解:∵AD∥BC,EF∥BC
∴AD∥BC∥EF
又∵AE=FC
∴AE2=EB×DF=36
3.
如图,在△ABC中,
DE∥BC.
A
B
C
D
E
(1)
如果AB
=
10,
AD=6,
AE=
5,那么
EC
的长是多少?
(2)如果AC=4
,AB=3,EC=1,那么
AD和BD的
长是多少?.
基础训练2
平行于三角形一边的直线的性质定理
3.
如图,在△ABC中,
DE∥BC.
A
B
C
D
E
(1)
如果AB
=
10,
AD=6,
AE=
5,那么
EC
的长是多少?
基础训练2
平行于三角形一边的直线的性质定理
〖方法一〗
解:∵在△ABC中,DE∥BC
3.
如图,在△ABC中,
DE∥BC.
A
B
C
D
E
(1)
如果AB
=
10,
AD=6,
AE=
5,那么
EC
的长是多少?
基础训练2
平行于三角形一边的直线的性质定理
〖方法二〗
解:∵在△ABC中,DE∥BC
A
B
C
D
E
3.
如图,在△ABC中,
DE∥BC.
(2)如果AC=3
,AB=4,EC=1,那么
AD和BD的长是多少?.
基础训练2
平行于三角形一边的直线的性质定理
4
3
1
解:∵在△ABC中,DE∥BC
?
本题还有其他方法,
大家不妨试试吧
数形结合
4.
如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.求证:OD∶OA=OE∶OB
证明:
DF∥AC,
EF∥BC,
练一练
变式训练2
平行于三角形一边的直线的性质定理
5.已知
∠A
=∠E=60°,
求:BD的长。
CB
=
4,
BE
AB
=
——
—
2
3
基础训练3
平行于三角形一边的直线的性质定理
B
D
E
A
C
解:∵∠A
=∠E=60°
∴AC∥DE
6.已知AC∥FG∥DE,BF=4,FD=3,
,
求CB的值
B
D
E
A
C
F
G
变式训练3
平行于三角形一边的直线的性质定理
解:∵FG∥DE
4
3
又∵FG∥AC
课堂小结
两条直线被一组平行线所截,所得的对应线段成比例
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例
基本事实
平行线分线段成比例
课堂小结
作业
必做
1.如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,求
的值
2.
如图,已知菱形
ABCD
内接于△AEF,AE=5cm,
AF
=
4
cm,求菱形的边长.
选做
27.2.1相似三角形的判定
第1课时
1.相似图形的定义:
我们把这些形状相同的图形,叫做相似图形。
回顾复习
2.(1)相似多边形的定义:
两个边数相同的多边形,如果它们的角分别
相等,边成比例,那么这两个多边形叫相似多边形。
(2)相似多边形的性质:
相似多边形的对应角相等,对应边成比例.
回顾复习
相似图形
相似多边形
相似三角形
§27.2.1
的判定
1.了解相似三角形的概念及表示方法。
2.理解并掌握平行线分线段成比例定理及平行于三角形一边的直线的性质定理【重点、难点】
学习目标
第一课时
平行线分线段成比例定理
相似三角形
_________________________
新知探究1
相似三角形的概念
相似三角形的定义:
在两个三角形中,如果这两个三角形的___________、____________则这两个______
叫做相似三角形.
三个角相等
三条边成比例
三角形
即如图,在△ABC
和△A'B'C'中,如果
∠A
=∠A',
∠B
=∠B',
∠C
=∠C'
A
B
C
A'
B'
C'
则__________________
且____________
△ABC
∽
△A'B'C'
A
B
C
A'
B'
C'
反之,如果△ABC
∽
△A'B'C',则________
∠A
=∠A'
∠B
=∠B',
∠C
=∠C'
_________________
=
k
即△ABC
与△A'B'C'的______为
k
.
或△A'B'C'与△ABC
的相似比为___
.
相似比
想一想:如果k=1,这两个三角形有怎样的关系
?
新知探究1
相似三角形的概念
相似三角形的性质:
相似三角形的对应角相等,对应边成比例
且________________
全等
小结归纳1
1.相似三角形的定义:
在两个三角形中,如果这两个三角形的三
个角相等,三条边成比例则两个三角形叫做相似三角形。
学习目标
1.了解相似三角形的概念及表示方法。
2.相似三角形的性质:
相似三角形的对应角相等,对应边成比例
新知探究2
相似三角形的判定
思考:有没有其他简单的办法判断两个三角形相似
∠A
=∠A',
∠B
=∠B',
∠C
=∠C'
①
A
B
C
A'
B'
C'
②
目前掌握的判定三角形相似的方法只有一个,即根据相似三角形的定义。
(定义法)
即若想判定△ABC
和
△A′B′C′
相似需要满足
在△ABC中,
DE∥BC
A
B
C
D
E
我们要证明这个结论.
你能
画出两个相似三角形吗?
直觉告诉我们,△ADE与△ABC相似.
只添一笔
新知探究2
相似三角形的判定
A
B
C
D
E
在△ABC中,DE∥BC
△ADE∽△ABC
先证明两个三角形的对应角相等.
∵在△ABC中,DE∥BC
∴∠ADE=∠B,
∠AED=∠C
即△ADE和△ABC的所有对应角相等
证明:
在△ADE与△ABC中,∠A=∠A
已知:
求证:
新知探究
相似三角形的判定
再证明两个三角形的对应边成比例(比相等).
A
B
C
D
E
在△ABC中,DE∥BC
△ADE∽△ABC
已知:
求证:
新知探究2
相似三角形的判定
(
)
平行线分线段成比例定理
任画两条直线l1,l2,再画三条与l1,l2都相交的平行
线l3
,
l4,
l5.分别与交于点A、B、C、D、E、F
DE,
EF的长度,
新知探究2
A
B
C
D
E
F
l3
l4
l5
l1
l2
请度量AB,
BC,
5
6
10
12
①
(
)
(
)
②
(
)
(
)
任画两条直线l1,l2,再画三条与l1,l2都相交的平行
线l3
,
l4,
l5.分别与交于点A、B、C、D、E、F
DE,
EF的长度,
新知探究2
A
B
C
D
E
F
l3
l4
l5
l1
l2
请度量AB,
BC,
5
6
10
12
(
)
③
平行线分线段成比例定理
任画两条直线l1,l2,再画三条与l1,l2都相交的平行
线l3
,
l4,
l5.分别与交于点A、B、C、D、E、F
(
)
(
)
(
)
①
③
②
?
?
?
?
?
?
新知探究2
A
B
C
D
E
F
l3
l4
l5
l1
l2
5
6
10
12
DE,
EF的长度,
请度量AB,
BC,
新知探究2
平行线分线段成比例定理
利用等积法证明平行线分线段成比例定理。
线段成比例。
平行线分线段成比例定理:
一组
三条
只要
就有
l3
//l4
//
l5
∴
∵
或
或
两条直线
被
平行线所截,
所得的对应
符号语言:
小结归纳2
…
A
B
C
l4
l5
l1
D
E
F
l2
l3
A(D)
B
C
E
F
把直线l2向左或向右任意平移,
这些线段依然成比例.
(使D与A重合)
把此图形抽取出来。
新知探究3
平行于三角形一边的直线的性质定理
图中有哪些成比例的线段?
A
B
C
E
F
新知探究3
平行于三角形一边的直线的性质定理
A
B
C
l4
l5
l1
D
E
F
l2
l3
A
B
C
(E)
F
D
(使B和E重合)
把直线l2向左或向右任意平移,
这些线段依然成比例.
把此图形抽取出来。
新知探究3
平行于三角形一边的直线的性质定理
图中有哪些成比例的线段?
A
B
C
F
D
新知探究3
平行于三角形一边的直线的性质定理
边的延长线),所得的
平行线分线段成比例定理的推论:
A
B
C
E
F
A
B
C
F
D
对应线段成比例.
平行于
三角形一边的直线
截其他两边
(或两
在三角形中只要具备平行条件就可以直接得到对应线段成比例
新知探究3
平行于三角形一边的直线的性质定理:
平行于三角形一边的直线的性质定理
“A
”型
“X
”型
小结归纳3
平行于三角形一边的直线的性质定理
在△ABC中,DE∥BC,
∴
∵
符号语言:(以“A”型为例)
边的延长线),所得的
对应线段成比例.
平行于
三角形一边的直线
截其他两边
(或两
…
平行线分线段成比例定理:
两条直线被一组______所截,所得的对应线段______
平行线
成比例
平行于三角形一边的直线的性质定理:
平行于三角形一边的直线截其他两边(或两边延长线),所得的______线段______.
对应
成比例
小结
1.已知l1∥l2∥l3,下列比例式中错误的是(
)
A.
B.
C.
D.
D
基础训练1
A
C
E
B
D
F
l2
l1
l3
平行线分线段成比例定理
2.已知梯形ABCD中,
AD∥BC,EF∥BC,AE=FC,
,
,求:AE的长.
∴AE=6.
练一练
变式训练1
平行线分线段成比例定理
A
E
C
D
F
B
解:∵AD∥BC,EF∥BC
∴AD∥BC∥EF
又∵AE=FC
∴AE2=EB×DF=36
3.
如图,在△ABC中,
DE∥BC.
A
B
C
D
E
(1)
如果AB
=
10,
AD=6,
AE=
5,那么
EC
的长是多少?
(2)如果AC=4
,AB=3,EC=1,那么
AD和BD的
长是多少?.
基础训练2
平行于三角形一边的直线的性质定理
3.
如图,在△ABC中,
DE∥BC.
A
B
C
D
E
(1)
如果AB
=
10,
AD=6,
AE=
5,那么
EC
的长是多少?
基础训练2
平行于三角形一边的直线的性质定理
〖方法一〗
解:∵在△ABC中,DE∥BC
3.
如图,在△ABC中,
DE∥BC.
A
B
C
D
E
(1)
如果AB
=
10,
AD=6,
AE=
5,那么
EC
的长是多少?
基础训练2
平行于三角形一边的直线的性质定理
〖方法二〗
解:∵在△ABC中,DE∥BC
A
B
C
D
E
3.
如图,在△ABC中,
DE∥BC.
(2)如果AC=3
,AB=4,EC=1,那么
AD和BD的长是多少?.
基础训练2
平行于三角形一边的直线的性质定理
4
3
1
解:∵在△ABC中,DE∥BC
?
本题还有其他方法,
大家不妨试试吧
数形结合
4.
如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.求证:OD∶OA=OE∶OB
证明:
DF∥AC,
EF∥BC,
练一练
变式训练2
平行于三角形一边的直线的性质定理
5.已知
∠A
=∠E=60°,
求:BD的长。
CB
=
4,
BE
AB
=
——
—
2
3
基础训练3
平行于三角形一边的直线的性质定理
B
D
E
A
C
解:∵∠A
=∠E=60°
∴AC∥DE
6.已知AC∥FG∥DE,BF=4,FD=3,
,
求CB的值
B
D
E
A
C
F
G
变式训练3
平行于三角形一边的直线的性质定理
解:∵FG∥DE
4
3
又∵FG∥AC
课堂小结
两条直线被一组平行线所截,所得的对应线段成比例
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例
基本事实
平行线分线段成比例
课堂小结
作业
必做
1.如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,求
的值
2.
如图,已知菱形
ABCD
内接于△AEF,AE=5cm,
AF
=
4
cm,求菱形的边长.
选做
