第七章 相交线与平行线 复习课件(16张PPT)
文档属性
| 名称 | 第七章 相交线与平行线 复习课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 224.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
第七章
相交线与平行线
一、构建本章知识结构
A
B
C
D
E
F
O
A
B
C
D
A
B
D
E
O
相交线
F
E
O
平行线
对顶角、补角、
余角的概念
及性质。
平行的条件;
平行的性质。
两个角的和是_____,称这两个角互为余角。
两个角的和是平角,称这两个角互为_____。
有公共顶点,两边互为反向延长线的两个
角叫做_______。
_________的余角相等;
同角或等角的____相等;
对顶角_____。
直角
补角
对顶角
同角或等角
补角
相等
概念、性质填空:
区别:条件与结论互换,
即:已知平行用特征,探索平行用判定。
平行线的判定方法:
平行线的性质:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补。
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行;
平行于同一直线的两直线平行。
a
b
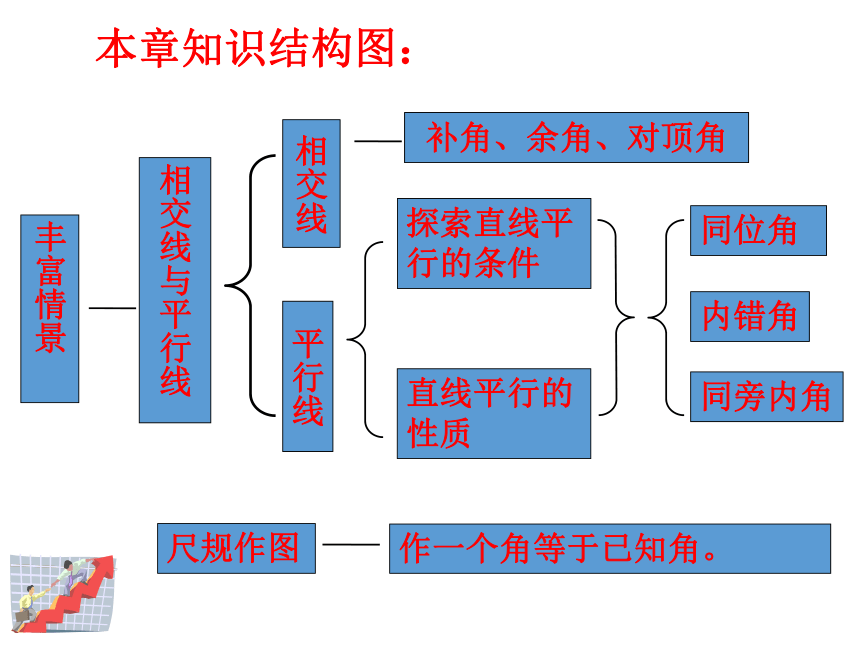
相交线与平行线
相交线
平行线
补角、余角、对顶角
丰富情景
直线平行的性质
探索直线平行的条件
同位角
内错角
同旁内角
本章知识结构图:
作一个角等于已知角。
尺规作图
二、强化知识、技能训练
a
d
c
b
3
1
2
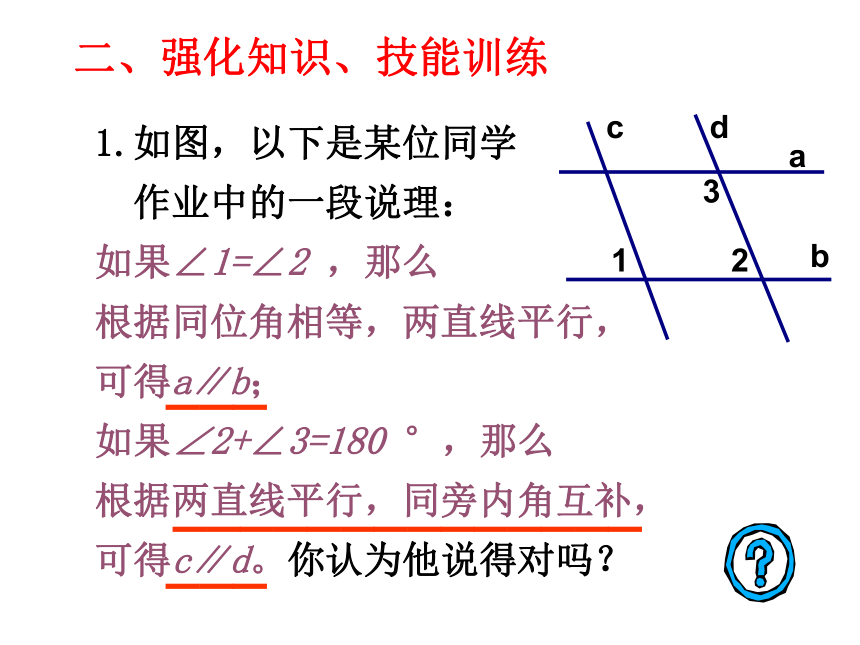
1.如图,以下是某位同学
作业中的一段说理:
如果∠1=∠2
,那么
根据同位角相等,两直线平行,
可得a∥b;
如果∠2+∠3=180
°,那么
根据两直线平行,同旁内角互补,
可得c∥d。你认为他说得对吗?
___
___
______________
E
3
O
A
B
C
D
2
1
2.若∠BOC=2∠1,
则∠1=______,
∠BOC=_______。
34°
60°
120
°
若OE⊥AB
,∠1=56°,
则∠3=____。
3 .
如图,在电线杆C点处引两根拉线固定电线杆,若∠1+∠2=90°,∠2+∠3=90°,那么∠1___∠3
(填
>,
=,
<
)
理由是_____________。
=
同角的余角相等
2
1
3
C
4.如图,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是北偏东42
°.甲、乙两地同时开工,若干天后公路准确接通,乙地所修公路的走向是南偏西多少度?为什么?
甲
乙
北
北
42
°
南偏西42
°
5.如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°。已知梯形的两底AD//BC,请你求出另外两个角的度数。(学生尝试用自己的方式书写说理过程)
A
D
B
C
115°
110°
∠A=115°
∠B=65
°
∠D=110°
∠C=70
°
三、运用本章知识、技能
解决一些简单问题:
1.(算算看)已知如图,OB⊥OA,直线CD过O,∠BOD=110°,
求∠AOC的度数?
∠BOD=110°
∠BOC=70°
∠AOC=20°
2.(考考你)图中如果AC∥BD
、
AE
∥BF
,那么∠A与∠B的关系
如何?你是怎样思考的?
AC∥BD,
AE
∥BF
∠A=∠B
∠A=∠DOE
∠B=∠DOE
∠A=∠B
3.(辨析与比较)如图,是两块相同的三角尺拼接成的一个图形,请找出图中互相平行的边。
∠1=
∠2
A1D∥BC1
∠3=
∠4
AB∥CD
若其中一块三角尺沿着重合的边向下滑动(如图所示),原来平行的边还平行吗?你知道其中的道理吗?
A
B
C
D
1
2
4
3
C
A1
B
D
A
C1
1
3
2
4
A
B
C
D
E
1
F
2
4.(操作与解释)如图,以点B为顶点,射线BC为一边,利用尺规作∠EBC,使得∠EBC=∠A,EB与AD一定平行吗?
四.拓展——探索与思考:
有一条长方形纸带,按如图所示沿AB折叠时,当∠1=30°求纸带重叠部分中∠CAB的度数。
A
B
C
1
2
3
4
E
F
∠CAB
=75°
第七章
相交线与平行线
一、构建本章知识结构
A
B
C
D
E
F
O
A
B
C
D
A
B
D
E
O
相交线
F
E
O
平行线
对顶角、补角、
余角的概念
及性质。
平行的条件;
平行的性质。
两个角的和是_____,称这两个角互为余角。
两个角的和是平角,称这两个角互为_____。
有公共顶点,两边互为反向延长线的两个
角叫做_______。
_________的余角相等;
同角或等角的____相等;
对顶角_____。
直角
补角
对顶角
同角或等角
补角
相等
概念、性质填空:
区别:条件与结论互换,
即:已知平行用特征,探索平行用判定。
平行线的判定方法:
平行线的性质:
两直线平行,同位角相等;
两直线平行,内错角相等;
两直线平行,同旁内角互补。
同位角相等,两直线平行;
内错角相等,两直线平行;
同旁内角互补,两直线平行;
平行于同一直线的两直线平行。
a
b
相交线与平行线
相交线
平行线
补角、余角、对顶角
丰富情景
直线平行的性质
探索直线平行的条件
同位角
内错角
同旁内角
本章知识结构图:
作一个角等于已知角。
尺规作图
二、强化知识、技能训练
a
d
c
b
3
1
2
1.如图,以下是某位同学
作业中的一段说理:
如果∠1=∠2
,那么
根据同位角相等,两直线平行,
可得a∥b;
如果∠2+∠3=180
°,那么
根据两直线平行,同旁内角互补,
可得c∥d。你认为他说得对吗?
___
___
______________
E
3
O
A
B
C
D
2
1
2.若∠BOC=2∠1,
则∠1=______,
∠BOC=_______。
34°
60°
120
°
若OE⊥AB
,∠1=56°,
则∠3=____。
3 .
如图,在电线杆C点处引两根拉线固定电线杆,若∠1+∠2=90°,∠2+∠3=90°,那么∠1___∠3
(填
>,
=,
<
)
理由是_____________。
=
同角的余角相等
2
1
3
C
4.如图,在甲、乙两地之间要修一条笔直的公路,从甲地测得公路的走向是北偏东42
°.甲、乙两地同时开工,若干天后公路准确接通,乙地所修公路的走向是南偏西多少度?为什么?
甲
乙
北
北
42
°
南偏西42
°
5.如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°。已知梯形的两底AD//BC,请你求出另外两个角的度数。(学生尝试用自己的方式书写说理过程)
A
D
B
C
115°
110°
∠A=115°
∠B=65
°
∠D=110°
∠C=70
°
三、运用本章知识、技能
解决一些简单问题:
1.(算算看)已知如图,OB⊥OA,直线CD过O,∠BOD=110°,
求∠AOC的度数?
∠BOD=110°
∠BOC=70°
∠AOC=20°
2.(考考你)图中如果AC∥BD
、
AE
∥BF
,那么∠A与∠B的关系
如何?你是怎样思考的?
AC∥BD,
AE
∥BF
∠A=∠B
∠A=∠DOE
∠B=∠DOE
∠A=∠B
3.(辨析与比较)如图,是两块相同的三角尺拼接成的一个图形,请找出图中互相平行的边。
∠1=
∠2
A1D∥BC1
∠3=
∠4
AB∥CD
若其中一块三角尺沿着重合的边向下滑动(如图所示),原来平行的边还平行吗?你知道其中的道理吗?
A
B
C
D
1
2
4
3
C
A1
B
D
A
C1
1
3
2
4
A
B
C
D
E
1
F
2
4.(操作与解释)如图,以点B为顶点,射线BC为一边,利用尺规作∠EBC,使得∠EBC=∠A,EB与AD一定平行吗?
四.拓展——探索与思考:
有一条长方形纸带,按如图所示沿AB折叠时,当∠1=30°求纸带重叠部分中∠CAB的度数。
A
B
C
1
2
3
4
E
F
∠CAB
=75°
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
