第七章 相交线与平行线 复习课件(19张PPT)
文档属性
| 名称 | 第七章 相交线与平行线 复习课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 80.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 17:09:17 | ||
图片预览




文档简介
(共19张PPT)
第七章
相交线与平行线
丰富情境
实际问题
相交线与
平行线
相交线
平行线
尺规作图——
作一条线段等于已知线段、作一个角等于已知角.以及简单应用.
相交线
补角
余角
对顶角
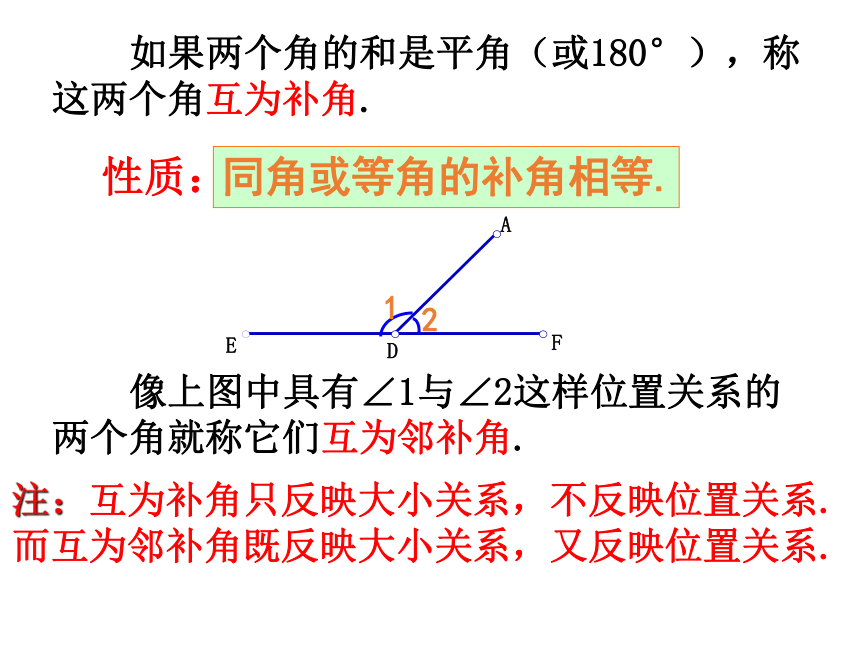
如果两个角的和是平角(或180°),称这两个角互为补角.
同角或等角的补角相等.
性质:
2
1
像上图中具有∠1与∠2这样位置关系的两个角就称它们互为邻补角.
注:互为补角只反映大小关系,不反映位置关系.而互为邻补角既反映大小关系,又反映位置关系.
如果两个角的和是直角(或90°),称这两个角互为余角.
同角或等角的余角相等.
性质:
注:互为余角只反映大小关系,不反映位置关系.
A
D
C
B
O
如图,直线AB与直线CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角.
对顶角相等.
性质:
注:对顶角既反映大小关系,又反映位置关系.
平行线
探索直线平行的条件
平行线的性质
图中识概念
:
“F”型中的同位角
“Z”字型中的内错角
“U”字型中的同旁内角
(2)同位角相等,两直线平行.
(1)平行线定义;
(3)内错角相等,两直线平行.
(4)同旁内角互补,两直线平行.
(5)如果两条直线都和第三条直线平行,那么这
两条直线也平行.
注:同位角,内错角,同旁内角均不是平行线所特有的.它们只反映角的位置关系,而不反映大小关系.
两直线平行的条件:
(1)两直线平行,同位角相等.
(2)两直线平行,内错角相等.
(3)两直线平行,同旁内角互补.
平行线的3个性质:
1、判断:
(1)两条不平行的线段,在同一平面内必相交.
(
)
(2)两条直线被第三条直线所截,内错角相等.
(
)
(3)相等的两个角为对顶角.
(
)
(4)两条直线相交,如果有两个角相等,那么这两个角是对顶角.
(
)
(5)两条直线被第三条直线所截,如果同位角相等,那么同旁内角互补.
(
)
×
×
×
×
√
(6)两条直线相交后,只有两对对顶角和一组邻补角,一组互余的角.
(
)
×
2、选择:
(1)下列说法中正确的是(
)
两条直线相交所成的角是对顶角.
有公共顶点的角是对顶角.
一个角的两个相邻补角是对顶角.
有一边互为反向延长线,且相等的两个角是对顶角.
C
(2)如图1,如果AD∥BC,则有①∠A+∠B=180°②∠B+∠C=180°
③
∠C+∠D=180°上述结论中正确的是(
)
只有①.
B.只有②.
C.只有③.
D.只有①和③.
图1
图2
α
D
(3)如图2,如果l1
∥l2
,AB⊥l1
,∠ABC=130°,那么∠α=(
)
A.60°
B.50°
C.40°
D.30°.
C
3.如图3,(1)指出OA是什么方向的一条射线?
(2)画出OA的相反方向,并说出它的方位.
60°
解:(1)OA是北偏东30°;
(2)OA的相反方向为南偏西30°.
A
东
北
西
南
60°
图3
4.如图4,HP平分∠EHD,∠1=55°,∠2=110°,
直线AB、CD平行吗?请说明理由.
∴
AB∥CD
解:∵PH平分∠EHD,∠1=55°(已知)
∴∠GHP=∠1=55°(角平分线定义)
∴∠GHD=110°
又∠2=110°(已知)
∴∠GHD=∠2(等量代换)
(同位角相等,两直线平行)
2
P
H
G
F
E
D
C
B
A
1
图4
5.如图5,已知∠1=25°,∠B=65°,AB⊥AC.
(1)AD与BC平行吗?请说明理由.
(2)AB与CD平行吗?如果平行,请说明理由;如果不平行,应再增加什么条件?
图5
1
解:∵
AB⊥AC
(已知)
∴∠BAC=90°(垂直定义)
∴∠BCA=∠BAC-∠B=25°
∵
∠B=65°
(已知)
∴∠BCA=∠1(等量代换)
∵
∠1=25°(已知)
∴AD∥BC(内错角相等,两直线平行)
6.如图,∠1=∠2,∠3=∠4,∠5=∠A.
求证:BE∥CF.
∵∠3=∠4,(已知)
∴AE∥BC.
(内错角相等,两直线平行)
∴∠EDC=∠5,
(两直线平行,内错角相等)
又∠5=∠A,(已知)
∴∠EDC=∠A,(等量代换)
∴DC∥AB.
(同位角相等,两直线平行)
∴∠5+∠2+∠3=180°.
(两直线平行,同旁内角互补)
∠1=∠2,(已知)
∴∠1+∠5+∠3=180°,(等量代换)
∴BE∥FC.
(同旁内角互补.两直线平行)
证明:
第七章
相交线与平行线
丰富情境
实际问题
相交线与
平行线
相交线
平行线
尺规作图——
作一条线段等于已知线段、作一个角等于已知角.以及简单应用.
相交线
补角
余角
对顶角
如果两个角的和是平角(或180°),称这两个角互为补角.
同角或等角的补角相等.
性质:
2
1
像上图中具有∠1与∠2这样位置关系的两个角就称它们互为邻补角.
注:互为补角只反映大小关系,不反映位置关系.而互为邻补角既反映大小关系,又反映位置关系.
如果两个角的和是直角(或90°),称这两个角互为余角.
同角或等角的余角相等.
性质:
注:互为余角只反映大小关系,不反映位置关系.
A
D
C
B
O
如图,直线AB与直线CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角.
对顶角相等.
性质:
注:对顶角既反映大小关系,又反映位置关系.
平行线
探索直线平行的条件
平行线的性质
图中识概念
:
“F”型中的同位角
“Z”字型中的内错角
“U”字型中的同旁内角
(2)同位角相等,两直线平行.
(1)平行线定义;
(3)内错角相等,两直线平行.
(4)同旁内角互补,两直线平行.
(5)如果两条直线都和第三条直线平行,那么这
两条直线也平行.
注:同位角,内错角,同旁内角均不是平行线所特有的.它们只反映角的位置关系,而不反映大小关系.
两直线平行的条件:
(1)两直线平行,同位角相等.
(2)两直线平行,内错角相等.
(3)两直线平行,同旁内角互补.
平行线的3个性质:
1、判断:
(1)两条不平行的线段,在同一平面内必相交.
(
)
(2)两条直线被第三条直线所截,内错角相等.
(
)
(3)相等的两个角为对顶角.
(
)
(4)两条直线相交,如果有两个角相等,那么这两个角是对顶角.
(
)
(5)两条直线被第三条直线所截,如果同位角相等,那么同旁内角互补.
(
)
×
×
×
×
√
(6)两条直线相交后,只有两对对顶角和一组邻补角,一组互余的角.
(
)
×
2、选择:
(1)下列说法中正确的是(
)
两条直线相交所成的角是对顶角.
有公共顶点的角是对顶角.
一个角的两个相邻补角是对顶角.
有一边互为反向延长线,且相等的两个角是对顶角.
C
(2)如图1,如果AD∥BC,则有①∠A+∠B=180°②∠B+∠C=180°
③
∠C+∠D=180°上述结论中正确的是(
)
只有①.
B.只有②.
C.只有③.
D.只有①和③.
图1
图2
α
D
(3)如图2,如果l1
∥l2
,AB⊥l1
,∠ABC=130°,那么∠α=(
)
A.60°
B.50°
C.40°
D.30°.
C
3.如图3,(1)指出OA是什么方向的一条射线?
(2)画出OA的相反方向,并说出它的方位.
60°
解:(1)OA是北偏东30°;
(2)OA的相反方向为南偏西30°.
A
东
北
西
南
60°
图3
4.如图4,HP平分∠EHD,∠1=55°,∠2=110°,
直线AB、CD平行吗?请说明理由.
∴
AB∥CD
解:∵PH平分∠EHD,∠1=55°(已知)
∴∠GHP=∠1=55°(角平分线定义)
∴∠GHD=110°
又∠2=110°(已知)
∴∠GHD=∠2(等量代换)
(同位角相等,两直线平行)
2
P
H
G
F
E
D
C
B
A
1
图4
5.如图5,已知∠1=25°,∠B=65°,AB⊥AC.
(1)AD与BC平行吗?请说明理由.
(2)AB与CD平行吗?如果平行,请说明理由;如果不平行,应再增加什么条件?
图5
1
解:∵
AB⊥AC
(已知)
∴∠BAC=90°(垂直定义)
∴∠BCA=∠BAC-∠B=25°
∵
∠B=65°
(已知)
∴∠BCA=∠1(等量代换)
∵
∠1=25°(已知)
∴AD∥BC(内错角相等,两直线平行)
6.如图,∠1=∠2,∠3=∠4,∠5=∠A.
求证:BE∥CF.
∵∠3=∠4,(已知)
∴AE∥BC.
(内错角相等,两直线平行)
∴∠EDC=∠5,
(两直线平行,内错角相等)
又∠5=∠A,(已知)
∴∠EDC=∠A,(等量代换)
∴DC∥AB.
(同位角相等,两直线平行)
∴∠5+∠2+∠3=180°.
(两直线平行,同旁内角互补)
∠1=∠2,(已知)
∴∠1+∠5+∠3=180°,(等量代换)
∴BE∥FC.
(同旁内角互补.两直线平行)
证明:
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
