人教版八年级数学下册18.1.2 平行四边形的判定课件(共16张PPT)
文档属性
| 名称 | 人教版八年级数学下册18.1.2 平行四边形的判定课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 441.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-06 21:51:54 | ||
图片预览



文档简介
(共16张PPT)
八年级数学(下)
18.1.2 平行四边形的判定
温馨提示
1.平行四边形的定义是什么?
两组对边分别平行的四边形是平行四边形.
分别平行
B
D
A
C
2.平行四边形还具有哪些性质呢?
(定义判定法)
定义既是性质,也是判定。
温故知新
从边、角、
对角线的角度
两组对边
思考角度 平行四边形的性质 几何语言 猜 想
边
角
对角线
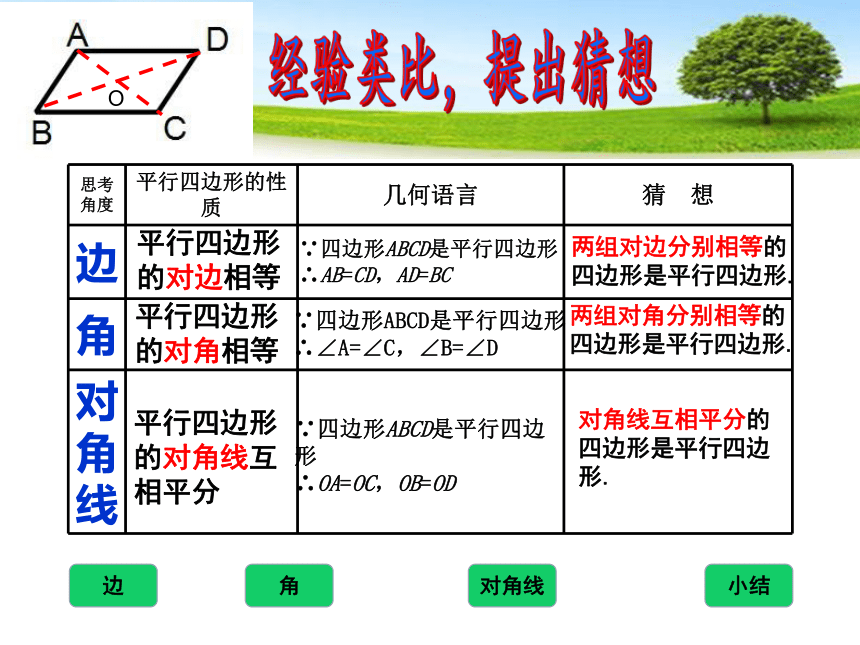
平行四边形的对边相等
平行四边形的对角相等
平行四边形的对角线互相平分
经验类比,提出猜想
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
O
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
小结
对角线
角
边
B
D
A
C
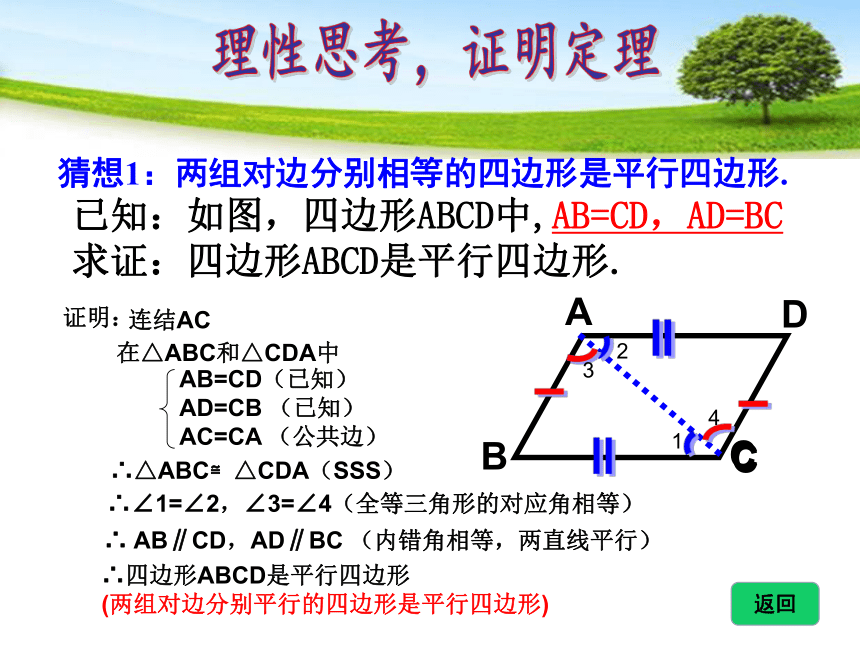
已知:如图,四边形ABCD中,AB=CD,AD=BC
求证:四边形ABCD是平行四边形.
C
猜想1:两组对边分别相等的四边形是平行四边形.
C
证明:
连结AC
在△ABC和△CDA中
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
AB=CD(已知)
AD=CB (已知)
AC=CA (公共边)
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
2
1
3
4
理性思考,证明定理
返回
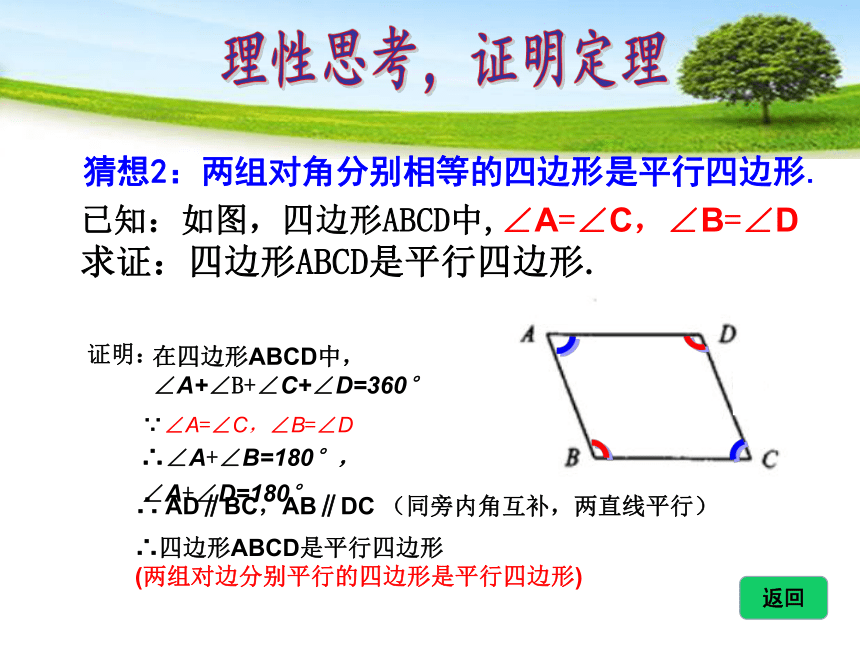
猜想2:两组对角分别相等的四边形是平行四边形.
已知:如图,四边形ABCD中,∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形.
证明:
在四边形ABCD中,
∠A+∠B+∠C+∠D=360°
∴∠A+∠B=180°,∠A+∠D=180°
∴ AD∥BC,AB∥DC (同旁内角互补,两直线平行)
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
∵∠A=∠C,∠B=∠D
理性思考,证明定理
返回
O
理性思考,证明定理
猜想3:对角线互相平分的四边形是平行四边形.
已知:如图,在四边形ABCD中,对角线AC、BD交于O,OA= OC, OB=OD.
求证:四边形ABCD是平行四边形
证明:
在△AOB和△COD中
∴△AOB≌△COD(SAS)
∴∠BAO=∠DCO
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
OA=OC(已知)
∠AOB=∠COD (对顶角相等)
OB=OD (已知)
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
同理可证:∠DAO=∠BCO
返回
x``xk
即时小结
平行四边形判定定理 文字表述 几何语言
∵ AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
两组对边分别相等的四边形是平行四边形. ∵ AB=CD,AD=BC
∴四边形ABCD是平行四边形
两组对角分别相等的四边形是平行四边形. ∵ ∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形
对角线互相平分的四边形是平行四边形. ∵OA= OC,OB=OD
∴四边形ABCD是平行四边形
两组对边分别平行的四边形是平行四边形.
判断下列四边形是否是平行四边形?并说明理由。
C
B
A
D
110°
110°
70°
°
4.8㎝
B
A
D
C
4.8㎝
7.6㎝
7.6㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
( )
是
( )
是
( )
是
小试牛刀
已知: 平行四边形ABCD的对角线AC、BD交于点O, E、F分别是OA、OC的中点。
求证:四边形BFDE是平行四边形。
应用新知
分析:要证四边形是平行四边形,看已知条件给的信息是对边、对角,还是对角线,然后进一步分析利用哪个途径证明更方便. 本题很明显是对角线条件比较突出,因此用对角线互相平分来证明比较简便。
证明:
∵ 四边形ABCD是平行四边形
∴ OA=OC,OB=OD
∵ E、F分别是OA、OC的中点
∴ OE=OF
而OB=OD
∴四边形BFDE是平行四边形
(对角线互相平分的四边形是平行四边形)
如图, ABCD的对角线AC、BD相交于点O,E,F是AC上的两点,并且AE=CF. 求证:四边形BFDE是平行四边形.
□
变式训练一
而OB=OD
证明:
∵ 四边形ABCD是平行四边形
∴ OA=OC,OB=OD
∵ AE=CF
∴ OA-AE=OC-CF
∴四边形BFDE是平行四边形
(对角线互相平分的四边形是平行四边形)
即:OE=OF
已知:如图,平行四边形ABCD的对角线 AC 、BD交于点O,E、F是直线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形。
D
E
F
B
A
C
O
直线
而OB=OD
证明:
∵ 四边形ABCD是平行四边形
∴ OA=OC,OB=OD
∵ AE=CF
∴ OA+AE=OC+CF
∴四边形BFDE是平行四边形
(对角线互相平分的四边形
是平行四边形)
即:OE=OF
变式训练二
平行四边形判定方法 角度 文字表述 几何语言
边
角
对角线
两组对边分别平行的四边形是平行四边形.
∵ AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
两组对边分别相等的四边形是平行四边形.
∵ AB=CD,AD=BC
∴四边形ABCD是平行四边形
两组对角分别相等的四边形是平行四边形.
∵ ∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形
对角线互相平分的四边形是平行四边形.
∵OA= OC,OB=OD
∴四边形ABCD是平行四边形
方法总结
1、本节课你学习了哪些知识?你有什么收获 ?
2、获得了哪些研究问题的方法?
(1).转化思想
(2).类比方法
作业
课后提升
已知:在平行四边形ABCD中,对角线AC 、BD相交于点0,M、N、P、Q分别是OA、OB、OC、OD的中点。
求证:四边形MNPQ是平行四边形 .
课后提升
Q
C
D
P
O
B
M
N
A
1.教科书第47页练习第1、2题;
2.习题18.1第5、12题。
作业:
下课了!
谢谢大家
再见
老师寄语
千锤成利器,百炼成纯钢!
八年级数学(下)
18.1.2 平行四边形的判定
温馨提示
1.平行四边形的定义是什么?
两组对边分别平行的四边形是平行四边形.
分别平行
B
D
A
C
2.平行四边形还具有哪些性质呢?
(定义判定法)
定义既是性质,也是判定。
温故知新
从边、角、
对角线的角度
两组对边
思考角度 平行四边形的性质 几何语言 猜 想
边
角
对角线
平行四边形的对边相等
平行四边形的对角相等
平行四边形的对角线互相平分
经验类比,提出猜想
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
O
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
∵四边形ABCD是平行四边形
∴∠A=∠C,∠B=∠D
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
小结
对角线
角
边
B
D
A
C
已知:如图,四边形ABCD中,AB=CD,AD=BC
求证:四边形ABCD是平行四边形.
C
猜想1:两组对边分别相等的四边形是平行四边形.
C
证明:
连结AC
在△ABC和△CDA中
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
AB=CD(已知)
AD=CB (已知)
AC=CA (公共边)
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
2
1
3
4
理性思考,证明定理
返回
猜想2:两组对角分别相等的四边形是平行四边形.
已知:如图,四边形ABCD中,∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形.
证明:
在四边形ABCD中,
∠A+∠B+∠C+∠D=360°
∴∠A+∠B=180°,∠A+∠D=180°
∴ AD∥BC,AB∥DC (同旁内角互补,两直线平行)
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
∵∠A=∠C,∠B=∠D
理性思考,证明定理
返回
O
理性思考,证明定理
猜想3:对角线互相平分的四边形是平行四边形.
已知:如图,在四边形ABCD中,对角线AC、BD交于O,OA= OC, OB=OD.
求证:四边形ABCD是平行四边形
证明:
在△AOB和△COD中
∴△AOB≌△COD(SAS)
∴∠BAO=∠DCO
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
OA=OC(已知)
∠AOB=∠COD (对顶角相等)
OB=OD (已知)
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
同理可证:∠DAO=∠BCO
返回
x``xk
即时小结
平行四边形判定定理 文字表述 几何语言
∵ AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
两组对边分别相等的四边形是平行四边形. ∵ AB=CD,AD=BC
∴四边形ABCD是平行四边形
两组对角分别相等的四边形是平行四边形. ∵ ∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形
对角线互相平分的四边形是平行四边形. ∵OA= OC,OB=OD
∴四边形ABCD是平行四边形
两组对边分别平行的四边形是平行四边形.
判断下列四边形是否是平行四边形?并说明理由。
C
B
A
D
110°
110°
70°
°
4.8㎝
B
A
D
C
4.8㎝
7.6㎝
7.6㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
( )
是
( )
是
( )
是
小试牛刀
已知: 平行四边形ABCD的对角线AC、BD交于点O, E、F分别是OA、OC的中点。
求证:四边形BFDE是平行四边形。
应用新知
分析:要证四边形是平行四边形,看已知条件给的信息是对边、对角,还是对角线,然后进一步分析利用哪个途径证明更方便. 本题很明显是对角线条件比较突出,因此用对角线互相平分来证明比较简便。
证明:
∵ 四边形ABCD是平行四边形
∴ OA=OC,OB=OD
∵ E、F分别是OA、OC的中点
∴ OE=OF
而OB=OD
∴四边形BFDE是平行四边形
(对角线互相平分的四边形是平行四边形)
如图, ABCD的对角线AC、BD相交于点O,E,F是AC上的两点,并且AE=CF. 求证:四边形BFDE是平行四边形.
□
变式训练一
而OB=OD
证明:
∵ 四边形ABCD是平行四边形
∴ OA=OC,OB=OD
∵ AE=CF
∴ OA-AE=OC-CF
∴四边形BFDE是平行四边形
(对角线互相平分的四边形是平行四边形)
即:OE=OF
已知:如图,平行四边形ABCD的对角线 AC 、BD交于点O,E、F是直线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形。
D
E
F
B
A
C
O
直线
而OB=OD
证明:
∵ 四边形ABCD是平行四边形
∴ OA=OC,OB=OD
∵ AE=CF
∴ OA+AE=OC+CF
∴四边形BFDE是平行四边形
(对角线互相平分的四边形
是平行四边形)
即:OE=OF
变式训练二
平行四边形判定方法 角度 文字表述 几何语言
边
角
对角线
两组对边分别平行的四边形是平行四边形.
∵ AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
两组对边分别相等的四边形是平行四边形.
∵ AB=CD,AD=BC
∴四边形ABCD是平行四边形
两组对角分别相等的四边形是平行四边形.
∵ ∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形
对角线互相平分的四边形是平行四边形.
∵OA= OC,OB=OD
∴四边形ABCD是平行四边形
方法总结
1、本节课你学习了哪些知识?你有什么收获 ?
2、获得了哪些研究问题的方法?
(1).转化思想
(2).类比方法
作业
课后提升
已知:在平行四边形ABCD中,对角线AC 、BD相交于点0,M、N、P、Q分别是OA、OB、OC、OD的中点。
求证:四边形MNPQ是平行四边形 .
课后提升
Q
C
D
P
O
B
M
N
A
1.教科书第47页练习第1、2题;
2.习题18.1第5、12题。
作业:
下课了!
谢谢大家
再见
老师寄语
千锤成利器,百炼成纯钢!
